
Velocity
Encyclopedia
In physics
, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant direction, typically constrains the object to motion in a straight path. A car moving at a constant 20 kilometers per hour in a circular path does not have a constant velocity. The rate of change in velocity is acceleration. Velocity is a vector physical quantity
; both magnitude and direction are required to define it. The scalar
absolute value
(magnitude
) of velocity is speed
, a quantity that is measured in metres per second (m/s or ms−1) when using the SI
(metric) system.
For example, "5 metres per second" is a scalar
and not a vector, whereas "5 metres per second east" is a vector. The average velocity v of an object moving through a displacement
 during a time interval
during a time interval  is described by the formula:
is described by the formula:

The rate of change of velocity is acceleration
– how an object's speed or direction of travel changes over time, and how it is changing at a particular point in time.
 at time
at time 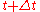 , can be computed as the derivative
, can be computed as the derivative
of position:
Average velocity magnitudes always smaller than or equal to average speed of a given particle.
Instantaneous velocity is always tangential to trajectory.
Slope of tangent of position or displacement time graph is instantaneous velocity and its slope of chord is average velocity.
The equation for an object's velocity can be obtained mathematically by evaluating the integral
of the equation for its acceleration beginning from some initial period time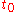 to some point in time later
to some point in time later  .
.
The final velocity v of an object which starts with velocity u and then accelerates at constant acceleration a for a period of time is:
is:

The average velocity of an object undergoing constant acceleration
is , where u is the initial velocity and v is the final velocity. To find the position, x, of such an accelerating object during a time interval,
, where u is the initial velocity and v is the final velocity. To find the position, x, of such an accelerating object during a time interval, 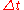 , then:
, then:
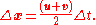
When only the object's initial velocity is known, the expression,
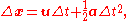
can be used.
This can be expanded to give the position at any time t in the following way:
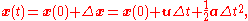
These basic equations for final velocity and position can be combined to form an equation that is independent of time, also known as Torricelli's equation
:

The above equations are valid for both Newtonian mechanics and special relativity
. Where Newtonian mechanics and special relativity differ is in how different observers would describe the same situation. In particular, in Newtonian mechanics, all observers agree on the value of t and the transformation rules for position create a situation in which all non-accelerating observers would describe the acceleration of an object with the same values. Neither is true for special relativity. In other words only relative velocity
can be calculated.
In Newtonian mechanics, the kinetic energy
(energy
of motion),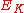 , of a moving object is linear with both its mass
, of a moving object is linear with both its mass
and the square of its velocity:

The kinetic energy is a scalar
quantity.
Escape velocity
is the minimum velocity a body must have in order to escape from the gravitational field of the earth.
To escape from the Earth's gravitational field an object must have greater kinetic energy than its gravitational potential energy. The value of the escape velocity from the Earth's surface is approximately 11100 m/s.
as determined in a single coordinate system. Relative velocity is fundamental in both classical and modern physics, since many systems in physics deal with the relative motion of two or more particles. In Newtonian mechanics, the relative velocity is independent of the chosen inertial reference frame. This is not the case anymore with special relativity
in which velocities depend on the choice of reference frame.
If an object A is moving with velocity vector v and an object B with velocity vector w, then the velocity of object A relative to object B is defined as the difference of the two velocity vectors:
Similarly the relative velocity of object B moving with velocity w, relative to object A moving with velocity v is:
Usually the inertial frame is chosen in which the latter of the two mentioned objects is in rest.
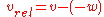 , if the two objects are moving in opposite directions, or:
, if the two objects are moving in opposite directions, or: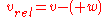 , if the two objects are moving in the same direction.
, if the two objects are moving in the same direction.
, a two-dimensional velocity is described by a radial velocity
, defined as the component of velocity away from or toward the origin (also known as velocity made good), and an angular velocity
, which is the rate of rotation about the origin (with positive quantities representing counter-clockwise rotation and negative quantities representing clockwise rotation, in a right-handed coordinate system).
The radial and angular velocities can be derived from the Cartesian velocity and displacement vectors by decomposing the velocity vector into radial and transverse components. The transverse velocity is the component of velocity along a circle centered at the origin.

where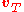 is the transverse velocity
is the transverse velocity is the radial velocity.
is the radial velocity.
The magnitude of the radial velocity is the dot product
of the velocity vector and the unit vector in the direction of the displacement.
where is displacement.
is displacement.
The magnitude of the transverse velocity is that of the cross product
of the unit vector in the direction of the displacement and the velocity vector. It is also the product of the angular speed and the magnitude of the displacement.
and the magnitude of the displacement.
such that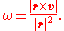
Angular momentum
in scalar form is the mass times the distance to the origin times the transverse velocity, or equivalently, the mass times the distance squared times the angular speed. The sign convention for angular momentum is the same as that for angular velocity.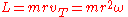
where is mass
is mass
The expression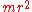 is known as moment of inertia
is known as moment of inertia
.
If forces are in the radial direction only with an inverse square dependence, as in the case of a gravitational orbit
, angular momentum is constant, and transverse speed is inversely proportional to the distance, angular speed is inversely proportional to the distance squared, and the rate at which area is swept out is constant. These relations are known as Kepler's laws of planetary motion
.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant direction, typically constrains the object to motion in a straight path. A car moving at a constant 20 kilometers per hour in a circular path does not have a constant velocity. The rate of change in velocity is acceleration. Velocity is a vector physical quantity
Physical quantity
A physical quantity is a physical property of a phenomenon, body, or substance, that can be quantified by measurement.-Definition of a physical quantity:Formally, the International Vocabulary of Metrology, 3rd edition defines quantity as:...
; both magnitude and direction are required to define it. The scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
(magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
) of velocity is speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
, a quantity that is measured in metres per second (m/s or ms−1) when using the SI
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
(metric) system.
For example, "5 metres per second" is a scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
and not a vector, whereas "5 metres per second east" is a vector. The average velocity v of an object moving through a displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
 during a time interval
during a time interval  is described by the formula:
is described by the formula:
The rate of change of velocity is acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
– how an object's speed or direction of travel changes over time, and how it is changing at a particular point in time.
Equation of motion
The velocity vector v of an object that has positions x(t) at time t and x at time
at time 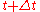 , can be computed as the derivative
, can be computed as the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of position:

Average velocity magnitudes always smaller than or equal to average speed of a given particle.
Instantaneous velocity is always tangential to trajectory.
Slope of tangent of position or displacement time graph is instantaneous velocity and its slope of chord is average velocity.
The equation for an object's velocity can be obtained mathematically by evaluating the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of the equation for its acceleration beginning from some initial period time
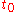 to some point in time later
to some point in time later  .
.The final velocity v of an object which starts with velocity u and then accelerates at constant acceleration a for a period of time
 is:
is:
The average velocity of an object undergoing constant acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
is
 , where u is the initial velocity and v is the final velocity. To find the position, x, of such an accelerating object during a time interval,
, where u is the initial velocity and v is the final velocity. To find the position, x, of such an accelerating object during a time interval, 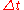 , then:
, then: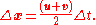
When only the object's initial velocity is known, the expression,
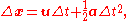
can be used.
This can be expanded to give the position at any time t in the following way:
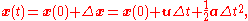
These basic equations for final velocity and position can be combined to form an equation that is independent of time, also known as Torricelli's equation
Torricelli's equation
Torricelli's equation is an equation created by Evangelista Torricelli to find the final velocity of an object moving with a constant acceleration without having a known time interval.The equation itself is: v_f^2 = v_i^2 + 2 a \Delta d \,- Derivation :...
:

The above equations are valid for both Newtonian mechanics and special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
. Where Newtonian mechanics and special relativity differ is in how different observers would describe the same situation. In particular, in Newtonian mechanics, all observers agree on the value of t and the transformation rules for position create a situation in which all non-accelerating observers would describe the acceleration of an object with the same values. Neither is true for special relativity. In other words only relative velocity
Relative velocity
In non-relativistic kinematics, relative velocity is the vector difference between the velocities of two objects, as evaluated in terms of a single coordinate system....
can be calculated.
In Newtonian mechanics, the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
(energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of motion),
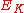 , of a moving object is linear with both its mass
, of a moving object is linear with both its massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
and the square of its velocity:

The kinetic energy is a scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
quantity.
Escape velocity
Escape velocity
In physics, escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero gravitational potential energy is negative since gravity is an attractive force and the potential is defined to be zero at infinity...
is the minimum velocity a body must have in order to escape from the gravitational field of the earth.
To escape from the Earth's gravitational field an object must have greater kinetic energy than its gravitational potential energy. The value of the escape velocity from the Earth's surface is approximately 11100 m/s.
Relative velocity
Relative velocity is a measurement of velocity between two objectsas determined in a single coordinate system. Relative velocity is fundamental in both classical and modern physics, since many systems in physics deal with the relative motion of two or more particles. In Newtonian mechanics, the relative velocity is independent of the chosen inertial reference frame. This is not the case anymore with special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
in which velocities depend on the choice of reference frame.
If an object A is moving with velocity vector v and an object B with velocity vector w, then the velocity of object A relative to object B is defined as the difference of the two velocity vectors:

Similarly the relative velocity of object B moving with velocity w, relative to object A moving with velocity v is:

Usually the inertial frame is chosen in which the latter of the two mentioned objects is in rest.
Scalar velocities
In the one dimensional case, the velocities are scalars and the equation is either: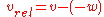 , if the two objects are moving in opposite directions, or:
, if the two objects are moving in opposite directions, or: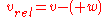 , if the two objects are moving in the same direction.
, if the two objects are moving in the same direction.Polar coordinates
In polar coordinatesPolar coordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
, a two-dimensional velocity is described by a radial velocity
Radial velocity
Radial velocity is the velocity of an object in the direction of the line of sight . In astronomy, radial velocity most commonly refers to the spectroscopic radial velocity...
, defined as the component of velocity away from or toward the origin (also known as velocity made good), and an angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
, which is the rate of rotation about the origin (with positive quantities representing counter-clockwise rotation and negative quantities representing clockwise rotation, in a right-handed coordinate system).
The radial and angular velocities can be derived from the Cartesian velocity and displacement vectors by decomposing the velocity vector into radial and transverse components. The transverse velocity is the component of velocity along a circle centered at the origin.

where
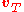 is the transverse velocity
is the transverse velocity is the radial velocity.
is the radial velocity.The magnitude of the radial velocity is the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of the velocity vector and the unit vector in the direction of the displacement.

where
 is displacement.
is displacement.The magnitude of the transverse velocity is that of the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of the unit vector in the direction of the displacement and the velocity vector. It is also the product of the angular speed
 and the magnitude of the displacement.
and the magnitude of the displacement.
such that
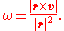
Angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
in scalar form is the mass times the distance to the origin times the transverse velocity, or equivalently, the mass times the distance squared times the angular speed. The sign convention for angular momentum is the same as that for angular velocity.
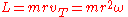
where
 is mass
is mass
The expression
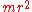 is known as moment of inertia
is known as moment of inertiaMoment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
.
If forces are in the radial direction only with an inverse square dependence, as in the case of a gravitational orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
, angular momentum is constant, and transverse speed is inversely proportional to the distance, angular speed is inversely proportional to the distance squared, and the rate at which area is swept out is constant. These relations are known as Kepler's laws of planetary motion
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
.
See also
- Escape velocityEscape velocityIn physics, escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero gravitational potential energy is negative since gravity is an attractive force and the potential is defined to be zero at infinity...
- Four-velocityFour-velocityIn physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
(relativistic version of velocity for Minkowski spacetime) - Group velocityGroup velocityThe group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
- HypervelocityHypervelocityThe term hypervelocity usually refers to a very high velocity, approximately over 3,000 meters per second . In particular, it refers to velocities so high that the strength of materials upon impact is very small compared to inertial stresses. Thus, even metals behave like fluids under hypervelocity...
- KinematicsKinematicsKinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
- Phase velocityPhase velocityThe phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
- Proper velocityProper velocityIn relativity, proper-velocity, also known as celerity, is an alternative to velocity for measuring motion. Whereas velocity relative to an observer is distance per unit time where both distance and time are measured by the observer, proper velocity relative to an observer divides observer-measured...
(in relativity, using traveler time instead of observer time) - RapidityRapidityIn relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...
(a version of velocity additive at relativistic speeds) - Relative velocityRelative velocityIn non-relativistic kinematics, relative velocity is the vector difference between the velocities of two objects, as evaluated in terms of a single coordinate system....
- Terminal velocityTerminal velocityIn fluid dynamics an object is moving at its terminal velocity if its speed is constant due to the restraining force exerted by the fluid through which it is moving....
- Velocity vs. time graph
External links
- Physicsclassroom.com, Speed and Velocity
- Introduction to Mechanisms (Carnegie Mellon UniversityCarnegie Mellon UniversityCarnegie Mellon University is a private research university in Pittsburgh, Pennsylvania, United States....
)

