Special relativity
Encyclopedia

Inertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
proposed in 1905 by Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
(after the considerable and independent contributions of Hendrik Lorentz
Hendrik Lorentz
Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
, Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
and others) in the paper "On the Electrodynamics of Moving Bodies".
It generalizes Galileo's principle of relativity
Galilean invariance
Galilean invariance or Galilean relativity is a principle of relativity which states that the fundamental laws of physics are the same in all inertial frames...
—that all uniform motion
Inertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
is relative, and that there is no absolute and well-defined state of rest (no privileged reference frames
Preferred frame
In theoretical physics, a preferred or privileged frame is usually a special hypothetical frame of reference in which the laws of physics might appear to be identifiably different from those in other frames....
)—from mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
to all the laws of physics, including both the laws of mechanics and of electrodynamics, whatever they may be. Special relativity incorporates the principle that the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
is the same for all inertial observers
Observer (special relativity)
The term observer in special relativity refers most commonly to an inertial reference frame. Less often it may refer to an arbitrary non-inertial reference frame; in particular, a Rindler frame is sometimes called an "accelerating observer". In such cases an inertial reference frame may be called...
regardless of the state of motion of the source.
This theory has a wide range of consequences which have been experimentally verified, including counter-intuitive ones such as length contraction
Length contraction
In physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer...
, time dilation
Time dilation
In the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at...
and relativity of simultaneity
Relativity of simultaneity
In physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur...
, contradicting the classical notion that the duration of the time interval between two events is equal for all observers. (On the other hand, it introduces the space-time interval, which is invariant
Invariant (physics)
In mathematics and theoretical physics, an invariant is a property of a system which remains unchanged under some transformation.-Examples:In the current era, the immobility of polaris under the diurnal motion of the celestial sphere is a classical illustration of physical invariance.Another...
.) Combined with other laws of physics, the two postulates of special relativity predict the equivalence of matter
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
and energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
, as expressed in the mass–energy equivalence formula E = mc2, where c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in a vacuum. The predictions of special relativity agree well with Newtonian mechanics in their common realm of applicability, specifically in experiments in which all velocities are small compared with the speed of light. Special relativity reveals that c is not just the velocity of a certain phenomenon—namely the propagation of electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
(light)—but rather a fundamental feature of the way space and time are unified as spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. One of the consequences of the theory is that it is impossible for any particle that has rest mass to be accelerated to the speed of light.
The theory was originally termed "special" because it applied the principle of relativity
Principle of relativity
In physics, the principle of relativity is the requirement that the equations describing the laws of physics have the same form in all admissible frames of reference....
only to the special case
Special case
In logic, especially as applied in mathematics, concept A is a special case or specialization of concept B precisely if every instance of A is also an instance of B, or equivalently, B is a generalization of A. For example, all circles are ellipses ; therefore the circle is a special case of the...
of inertial reference frames, i.e. frames of reference in uniform relative motion with respect to each other. Einstein developed general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
to apply the principle in the more general case, that is, to any frame so as to handle general coordinate transformations
General covariance
In theoretical physics, general covariance is the invariance of the form of physical laws under arbitrary differentiable coordinate transformations...
, and that theory includes the effects of gravity.
The term is currently used more generally to refer to any case in which gravitation is not significant. General relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
is the generalization of special relativity to include gravitation. In general relativity, gravity is described using noneuclidean geometry, so that gravitational effects are represented by curvature of spacetime; special relativity is restricted to flat spacetime. Just as the curvature of the earth's surface is not noticeable in everyday life, the curvature of spacetime can be neglected on small scales, so that locally, special relativity is a valid approximation to general relativity. The presence of gravity becomes undetectable in a sufficiently small, free-falling laboratory.
Postulates
Einstein discerned two fundamental propositions that seemed to be the most assured, regardless of the exact validity of the (then) known laws of either mechanics or electrodynamics. These propositions were the constancy of the speed of light and the independence of physical laws (especially the constancy of the speed of light) from the choice of inertial system. In his initial presentation of special relativity in 1905 he expressed these postulates as:- The Principle of Relativity – The laws by which the states of physical systems undergo change are not affected, whether these changes of state be referred to the one or the other of two systems in uniform translatory motion relative to each other.
- The Principle of Invariant Light Speed – "... light is always propagated in empty space with a definite velocity [speed] c which is independent of the state of motion of the emitting body." (from the preface). That is, light in vacuum propagates with the speed c (a fixed constant, independent of direction) in at least one system of inertial coordinates (the "stationary system"), regardless of the state of motion of the light source.
The derivation of special relativity depends not only on these two explicit postulates, but also on several tacit assumptions (made in almost all theories of physics
Duhem–Quine thesis
The Duhem–Quine thesis is that it is impossible to test a scientific hypothesis in isolation, because an empirical test of the hypothesis requires one or more background assumptions...
), including the isotropy
Isotropy
Isotropy is uniformity in all orientations; it is derived from the Greek iso and tropos . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix an, hence anisotropy. Anisotropy is also used to describe situations where properties vary...
and homogeneity
Homogeneity (physics)
In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity...
of space and the independence of measuring rods and clocks from their past history.
Following Einstein's original presentation of special relativity in 1905, many different sets of postulates have been proposed in various alternative derivations. However, the most common set of postulates remains those employed by Einstein in his original paper. A more mathematical statement of the Principle of Relativity made later by Einstein, which introduces the concept of simplicity not mentioned above is:
Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
provided the mathematical framework for relativity theory by proving that Lorentz transformations are a subset of his Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
of symmetry transformations. Einstein later derived these transformations from his axioms.
Many of Einstein's papers present derivations of the Lorentz transformation based upon these two principles.
Einstein consistently based the derivation of Lorentz invariance (the essential core of special relativity) on just the two basic principles of relativity and light-speed invariance. He wrote:
Thus many modern treatments of special relativity base it on the single postulate of universal Lorentz covariance, or, equivalently, on the single postulate of Minkowski spacetime.
From the principle of relativity alone without assuming the constancy of the speed of light (i.e. using the isotropy of space and the symmetry implied by the principle of special relativity) one can show that the space-time transformations between inertial frames are either Euclidean, Galilean, or Lorentzian. In the Lorentzian case, one can then obtain relativistic interval conservation and a certain finite limiting speed. Experiments suggest that this speed is the speed of light in vacuum.
The constancy of the speed of light was motivated by Maxwell's theory of electromagnetism and the lack of evidence for the luminiferous ether. There is conflicting evidence on the extent to which Einstein was influenced by the null result of the Michelson-Morley experiment
Michelson-Morley experiment
The Michelson–Morley experiment was performed in 1887 by Albert Michelson and Edward Morley at what is now Case Western Reserve University in Cleveland, Ohio. Its results are generally considered to be the first strong evidence against the theory of a luminiferous ether and in favor of special...
. In any case, the null result of the Michelson–Morley experiment helped the notion of the constancy of the speed of light gain widespread and rapid acceptance.
Mass–energy equivalence
In addition to the papers referenced above—which give derivations of the Lorentz transformation and describe the foundations of special relativity—Einstein also wrote at least four papers giving heuristic arguments for the equivalence (and transmutability) of mass and energy, for E = mc2.Mass–energy equivalence is a consequence of special relativity. The energy and momentum, which are separate in Newtonian mechanics, form a four-vector
Four-vector
In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
in relativity, and this relates the time component (the energy) to the space components (the momentum) in a nontrivial way. For an object at rest, the energy-momentum four-vector is (E, 0, 0, 0): it has a time component which is the energy, and three space components which are zero. By changing frames with a Lorentz transformation in the x direction with a small value of the velocity v, the energy momentum four-vector becomes (E, Ev/c2, 0, 0). The momentum is equal to the energy multiplied by the velocity divided by c2. As such, the Newtonian mass of an object, which is the ratio of the momentum to the velocity for slow velocities, is equal to E/c2.
The energy and momentum are properties of matter and radiation, and it is impossible to deduce that they form a four-vector just from the two basic postulates of special relativity by themselves, because these don't talk about matter or radiation, they only talk about space and time. The derivation therefore requires some additional physical reasoning. In his 1905 paper, Einstein used the additional principles that Newtonian mechanics should hold for slow velocities, so that there is one energy scalar and one three-vector momentum at slow velocities, and that the conservation law for energy and momentum is exactly true in relativity. Furthermore, he assumed that the energy of light is transformed by the same Doppler-shift factor as its frequency, which he had previously shown to be true based on Maxwell's equations. The first of Einstein's papers on this subject was "Does the Inertia of a Body Depend upon its Energy Content?" in 1905. Although Einstein's argument in this paper is nearly universally accepted by physicists as correct, even self-evident, many authors over the years have suggested that it is wrong. Other authors suggest that the argument was merely inconclusive because it relied on some implicit assumptions.
Einstein acknowledged the controversy over his derivation in his 1907 survey paper on special relativity. There he notes that it is problematic to rely on Maxwell's equations for the heuristic mass–energy argument. The argument in his 1905 paper can be carried out with the emission of any massless particles, but the Maxwell equations are implicitly used to make it obvious that the emission of light in particular can be achieved only by doing work. To emit electromagnetic waves, all you have to do is shake a charged particle, and this is clearly doing work, so that the emission is of energy.
Lack of an absolute reference frame
The principle of relativityPrinciple of relativity
In physics, the principle of relativity is the requirement that the equations describing the laws of physics have the same form in all admissible frames of reference....
, which states that there is no preferred inertial reference frame, dates back to Galileo
Galileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
, and was incorporated into Newtonian Physics. However, in the late 19th century, the existence of electromagnetic waves
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
led physicists to suggest that the universe was filled with a substance known as "aether
Luminiferous aether
In the late 19th century, luminiferous aether or ether, meaning light-bearing aether, was the term used to describe a medium for the propagation of light....
", which would act as the medium through which these waves, or vibrations travelled. The aether was thought to constitute an absolute reference frame
Preferred frame
In theoretical physics, a preferred or privileged frame is usually a special hypothetical frame of reference in which the laws of physics might appear to be identifiably different from those in other frames....
against which speeds could be measured, and could be considered fixed and motionless. Aether supposedly had some wonderful properties: it was sufficiently elastic that it could support electromagnetic waves, and those waves could interact with matter, yet it offered no resistance to bodies passing through it. The results of various experiments, including the Michelson–Morley experiment, indicated that the Earth was always 'stationary' relative to the aether – something that was difficult to explain, since the Earth is in orbit around the Sun. Einstein's solution was to discard the notion of an aether and an absolute state of rest. Special relativity is formulated so as to not assume that any particular frame of reference is special; rather, in relativity, any reference frame moving with uniform motion will observe the same laws of physics. In particular, the speed of light in a vacuum is always measured to be c, even when measured by multiple systems that are moving at different (but constant) velocities.
Consequences
Einstein has said that all of the consequences of special relativity can be derived from examination of the Lorentz transformations.These transformations, and hence special relativity, lead to different physical predictions than those of Newtonian mechanics when relative velocities become comparable to the speed of light. The speed of light is so much larger than anything humans encounter that some of the effects
predicted by relativity are initially counter-intuitive:
- Time dilationTime dilationIn the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at...
– the time lapse between two events is not invariant from one observer to another, but is dependent on the relative speeds of the observers' reference frames (e.g., the twin paradoxTwin paradoxIn physics, the twin paradox is a thought experiment in special relativity, in which a twin makes a journey into space in a high-speed rocket and returns home to find he has aged less than his identical twin who stayed on Earth...
which concerns a twin who flies off in a spaceship traveling near the speed of light and returns to discover that his or her twin sibling has aged much more). - Relativity of simultaneityRelativity of simultaneityIn physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur...
– two events happening in two different locations that occur simultaneously in the reference frame of one inertial observer, may occur non-simultaneously in the reference frame of another inertial observer (lack of absolute simultaneity). - Lorentz contraction – the dimensions (e.g., length) of an object as measured by one observer may be smaller than the results of measurements of the same object made by another observer (e.g., the ladder paradoxLadder paradoxThe ladder paradox is a thought experiment in special relativity. It involves a ladder travelling horizontally and undergoing a length contraction, the result of which being that it can fit into a much smaller garage...
involves a long ladder traveling near the speed of light and being contained within a smaller garage). - Composition of velocitiesVelocity-addition formulaIn physics, a velocity-addition formula is an equation that relates the velocities of moving objects in different reference frames.- Galilean addition of velocities :...
– velocities (and speeds) do not simply 'add', for example if a rocket is moving at the speed of light relative to an observer, and the rocket fires a missile at of the speed of light relative to the rocket, the missile does not exceed the speed of light relative to the observer. (In this example, the observer would see the missile travel with a speed of the speed of light.) - Thomas rotation - the orientation of an object (i.e. the alignment of its axes with the observer's axes) may be different for different observers. Unlike other relativistic effects, this effect becomes quite significant at fairly low velocities as can be seen in the spin of moving particles.
- InertiaInertiaInertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...
and momentum – as an object's speed approaches the speed of light from an observer's point of view, its mass appears to increase thereby making it more and more difficult to accelerate it from within the observer's frame of reference. - Equivalence of massMassMass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
and energyEnergyIn physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
, E = mc2 – The energy content of an object at rest with mass m equals mc2. Conservation of energy implies that, in any reaction, a decrease of the sum of the masses of particles must be accompanied by an increase in kinetic energies of the particles after the reaction. Similarly, the mass of an object can be increased by taking in kinetic energies.
Reference frames, coordinates and the Lorentz transformation

Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
". The term reference frame as used here is an observational perspective in space at rest, or in uniform motion, from which a position can be measured along 3 spatial axes. In addition, a reference frame has the ability to determine measurements of the time of events using a 'clock' (any reference device with uniform periodicity).
An event is an occurrence that can be assigned a single unique time and location in space relative to a reference frame: it is a "point" in space-time
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. Since the speed of light is constant in relativity in each and every reference frame, pulses of light can be used to unambiguously measure distances and refer back the times that events occurred to the clock, even though light takes time to reach the clock after the event has transpired.
For example, the explosion of a firecracker may be considered to be an "event". We can completely specify an event by its four space-time coordinates: The time of occurrence and its 3-dimensional spatial location define a reference point. Let's call this reference frame S.
In relativity theory we often want to calculate the position of a point from a different reference point.
Suppose we have a second reference frame S′, whose spatial axes and clock exactly coincide with that of S at time zero, but it is moving at a constant velocity v with respect to S along the x-axis.
Since there is no absolute reference frame in relativity theory, a concept of 'moving' doesn't strictly exist, as everything is always moving with respect to some other reference frame. Instead, any two frames that move at the same speed in the same direction are said to be comoving. Therefore S and S′ are not comoving.
Let's define the event to have space-time coordinates (t,x,y,z) in system S and (t′,x′,y′,z′) in S′. Then the Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
specifies that these coordinates are related in the following way:
-

where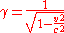
is the Lorentz factorLorentz factorThe Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
and c is the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in a vacuum.
The y and z coordinates are unaffected; only the x and t axes transformed. These Lorentz transformations form a one-parameter groupOne-parameter groupIn mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
of linear mappings, that parameter being called rapidityRapidityIn relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...
.
A quantity invariant under Lorentz transformations is known as a Lorentz scalarLorentz scalarIn physics, a Lorentz scalar is a scalar which is invariant under a Lorentz transformation. A Lorentz scalar may be generated from multiplication of vectors or tensors...
.
The Lorentz transformation given above is for the particular case in which the velocity v of S′ with respect to S is parallel to the x-axis. For the Lorentz transformation in the general case, suppose the velocity of S′ with respect to S is v. Denote the space-time coordinates of an event in S by (t,r) (instead of (t,x,y,z)). Then the coordinates (t′,r′) of this event in S′ are given by:

where vT denotes the transpose of v, , and P(v) denotes the projection onto the direction of v.
Simultaneity
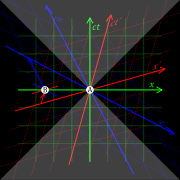
From the first equation of the Lorentz transformation in terms of coordinate differences
it is clear that two events that are simultaneous in frame S (satisfying ), are not necessarily simultaneous in another inertial frame S′ (satisfying ). Only if these events are colocal in frame S (satisfying ), will they be simultaneous in another frame S′.
Time dilation and length contraction
Writing the Lorentz transformation and its inverse in terms of coordinate differences, where for instance one event has coordinates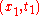 and
and 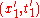 , another event has coordinates
, another event has coordinates  and
and 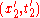 , and the differences are defined as
, and the differences are defined as  , we get
, we get
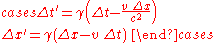
and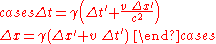
Suppose a clockClockA clock is an instrument used to indicate, keep, and co-ordinate time. The word clock is derived ultimately from the Celtic words clagan and clocca meaning "bell". A silent instrument missing such a mechanism has traditionally been known as a timepiece...
is at rest in the unprimed system S. Two different ticks of this clock are then characterized by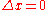 . To find the relation between the times between these ticks as measured in both systems, the first equation can be used to find:
. To find the relation between the times between these ticks as measured in both systems, the first equation can be used to find:
-
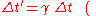 for events satisfying
for events satisfying 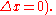
This shows that the time ( ) between the two ticks as seen in the frame in which the clock is moving (S'), is longer than the time (
) between the two ticks as seen in the frame in which the clock is moving (S'), is longer than the time (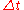 ) between these ticks as measured in the rest frame of the clock (S). This phenomenon is called time dilationTime dilationIn the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at...
) between these ticks as measured in the rest frame of the clock (S). This phenomenon is called time dilationTime dilationIn the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at...
. Time dilation explains a number of physical phenomena; for example, the decay rate of muonMuonThe muon |mu]] used to represent it) is an elementary particle similar to the electron, with a unitary negative electric charge and a spin of ½. Together with the electron, the tau, and the three neutrinos, it is classified as a lepton...
s produced by cosmic rays impinging on the Earth's atmosphere.
Similarly, suppose a measuring rodMeasuring rodA measuring rod is a tool used to physically measure lengths and survey areas of various sizes. Most measuring rods are round or square sectioned, however they can be flat boards. Some have markings at regular intervals...
is at rest and aligned along the x-axis in the unprimed system S. In this system, the length of this rod is written as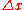 . To measure the length of this rod in the system S', in which the clock is moving, the distances
. To measure the length of this rod in the system S', in which the clock is moving, the distances 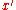 to the end points of the rod must be measured simultaneously in that system S'. In other words, the measurement is characterized by
to the end points of the rod must be measured simultaneously in that system S'. In other words, the measurement is characterized by 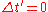 , which can be combined with the fourth equation to find the relation between the lengths
, which can be combined with the fourth equation to find the relation between the lengths 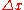 and
and  :
:
-
 for events satisfying
for events satisfying 
This shows that the length ( ) of the rod as measured in the frame in which the clock is moving (S'), is shorter than the length (
) of the rod as measured in the frame in which the clock is moving (S'), is shorter than the length (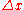 ) in its own rest frame (S). This phenomenon is called length contractionLength contractionIn physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer...
) in its own rest frame (S). This phenomenon is called length contractionLength contractionIn physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer...
or Lorentz contraction.
These effects are not merely appearances; they are explicitly related to our way of measuring time intervals between events which occur at the same place in a given coordinate system (called "co-local" events). These time intervals will be different in another coordinate system moving with respect to the first, unless the events are also simultaneous. Similarly, these effects also relate to our measured distances between separated but simultaneous events in a given coordinate system of choice. If these events are not co-local, but are separated by distance (space), they will not occur at the same spatial distance from each other when seen from another moving coordinate system. However, the space-time interval will be the same for all observers. The underlying reality remains the same. Only our perspective changes.
How far can one travel from the Earth?
Since one can not travel faster than light, one might conclude that a human can never travel further from Earth than 40 light years, if the traveler is active between the age of 20 and 60. One would easily think that a traveller would never be able to reach more than the very few solar systems which exist within the limit of 20-40 light years from the earth. But that would be a mistaken conclusion. Because of time dilation, he can travel thousands of light years during his 40 active years. If the spaceship accelerates at a constant 1G, he will after a little less than a year (mathematically) reach almost the speed of light, but time dilation will increase his life span to thousands of years, seen from the reference system of the Solar System, but his subjective lifespan will not thereby change. If he returns to Earth he will land thousands of years into its future. Even if he should accelerate for a longer period, his speed will not be seen as higher than the speed of light by observers on Earth, and he will not measure his speed as being higher than the speed of light. This is because he will see a length contraction of the universe in his direction of travel. And during the journey, people on Earth will experience much more time than he does. So, although his (ordinary) speed cannot exceed c, his four-velocity (distance as seen by Earth divided by his proper (i.e. subjective) time) can be much greater than c. This is similar to the fact that a muon can travel much further than c times its half-lifeHalf-lifeHalf-life, abbreviated t½, is the period of time it takes for the amount of a substance undergoing decay to decrease by half. The name was originally used to describe a characteristic of unstable atoms , but it may apply to any quantity which follows a set-rate decay.The original term, dating to...
(when at rest), if it is traveling close to c.
Causality and prohibition of motion faster than light
In diagram 2 the interval AB is 'time-like'; i.e., there is a frame of reference in which events A and B occur at the same location in space, separated only by occurring at different times. If A precedes B in that frame, then A precedes B in all frames. It is hypothetically possible for matter (or information) to travel from A to B, so there can be a causal relationship (with A the cause and B the effect).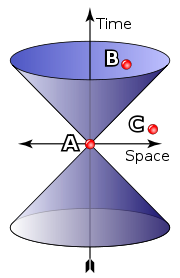
The interval AC in the diagram is 'space-like'; i.e., there is a frame of reference in which events A and C occur simultaneously, separated only in space. However there are also frames in which A precedes C (as shown) and frames in which C precedes A. If it were possible for a cause-and-effect relationship to exist between events A and C, then paradoxes of causality would result. For example, if A was the cause, and C the effect, then there would be frames of reference in which the effect preceded the cause. Although this in itself won't give rise to a paradox, one can show that faster than light signals can be sent back into one's own past. A causal paradox can then be constructed by sending the signal if and only if no signal was received previously.
Therefore, if causalityCausalityCausality is the relationship between an event and a second event , where the second event is understood as a consequence of the first....
is to be preserved, one of the consequences of special relativity is that no information signal or material object can travel faster than light in a vacuum. However, some things can still move faster than light. For example, the location where the beam of a search light hits the bottom of a cloud can move faster than light when the search light is turned rapidly.
Even without considerations of causality, there are other strong reasons why faster-than-light travel is forbidden by special relativity. For example, if a constant force is applied to an object for a limitless amount of time, then integrating F = dp/dt gives a momentum that grows without bound, but this is simply because approaches infinityInfinityInfinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
approaches infinityInfinityInfinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
as v approaches c. To an observer who is not accelerating, it appears as though the object's inertia is increasing, so as to produce a smaller acceleration in response to the same force. This behavior is in fact observed in particle accelerators, where each charged particle is accelerated by the electromagnetic force.
Theoretical and experimental tunneling studies carried out by Günter NimtzGünter NimtzGünter Nimtz is a German physicist, working at the 2nd Physics Institute at the University of Cologne in Germany. He has investigated narrow-gap semiconductors and liquid crystals and was engaged in several interdisciplinary studies on the effect of non-ionizing electromagnetic radiation in...
and Petrissa Eckle claimed that under special conditions signals may travel faster than light. It was measured that fiber digital signals were traveling up to 5 times c and a zero-time tunneling electron carried the information that the atom is ionizedIonizationIonization is the process of converting an atom or molecule into an ion by adding or removing charged particles such as electrons or other ions. This is often confused with dissociation. A substance may dissociate without necessarily producing ions. As an example, the molecules of table sugar...
, with photons, phononPhononIn physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
s and electrons spending zero time in the tunneling barrier. According to Nimtz and Eckle, in this superluminal process only the Einstein causality and the Special Relativity but not the primitive causality are violated: Superluminal propagation does not result in any kind of time travel. Several scientists have, however, stated not only that Nimtz' interpretations were erroneous, but that the experiment actually provided a trivial experimental confirmation of the Special relativity theory.
In September 2011, a paper from the OPERAOPERA ExperimentThe Oscillation Project with Emulsion-tRacking Apparatus is a scientific experiment for detecting tau neutrinos from muon neutrino oscillations. It is a collaboration between CERN in Geneva, Switzerland, and the Laboratori Nazionali del Gran Sasso in Gran Sasso, Italy and uses the CERN Neutrinos...
collaboration at CERN reported the OPERA neutrino anomalyOPERA neutrino anomalyThe OPERA neutrino anomaly is the detection of apparently faster-than-light neutrinos by the OPERA experiment as publicly announced in September 2011. The detection is anomalous because speeds exceeding that of light in a vacuum are generally thought to violate special relativity, a prevailing...
wherein muon neutrinos sent 730 kilometers (454 miles) from near Geneva, Switzerland to the Gran Sasso National LaboratoryLaboratori Nazionali del Gran SassoLaboratori Nazionali del Gran Sasso is a particle physics laboratory of the INFN, situated near the Gran Sasso mountain in Italy, between the towns of L'Aquila and Teramo, about 120 km from Rome. In addition to a surface portion of the laboratory, there are extensive underground facilities...
in ItalyItalyItaly , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
seemed to be traveling faster than light by a factor of approximately 1 in 40,000, a statistic with 6.0-sigma significance.
Composition of velocities
If the observer in S sees an object moving along the x axis at velocity u, then the observer in the S' system, a frame of reference moving at velocity v in the x direction with respect to S, will see the object moving with velocity u' where

This equation can be derived from the space and time transformations above.

Notice that if the object were moving at the speed of light in the S system (i.e. ), then it would also be moving at the speed of light in the S' system. Also, if both u and v are small with respect to the speed of light, we will recover the intuitive Galilean transformation of velocities:
), then it would also be moving at the speed of light in the S' system. Also, if both u and v are small with respect to the speed of light, we will recover the intuitive Galilean transformation of velocities:  .
.
The usual example given is that of a train (call it system ) traveling due east with a velocity
) traveling due east with a velocity  with respect to the tracks (system
with respect to the tracks (system 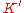 ). A child inside the train throws a baseball due east with a velocity
). A child inside the train throws a baseball due east with a velocity  with respect to the train. In classical physics, an observer at rest on the tracks will measure the velocity of the baseball as
with respect to the train. In classical physics, an observer at rest on the tracks will measure the velocity of the baseball as  . In special relativity, this is no longer true. Instead, an observer on the tracks will measure the velocity of the baseball as
. In special relativity, this is no longer true. Instead, an observer on the tracks will measure the velocity of the baseball as 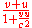 . If
. If  and
and  are small compared to
are small compared to  , then the above expression approaches the classical sum
, then the above expression approaches the classical sum  .
.
More generally, the baseball need not travel in the same direction as the train. To obtain the general formula for Einstein velocity addition, suppose an observer at rest in system measures the velocity of an object as
measures the velocity of an object as  . Let
. Let  be an inertial system such that the relative velocity of
be an inertial system such that the relative velocity of  to
to 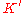 is
is  , where
, where  and
and  are now vectors in
are now vectors in  . An observer at rest in
. An observer at rest in 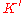 will then measure the velocity of the object as
will then measure the velocity of the object as

where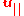 and
and 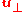 are the components of
are the components of  parallel and perpendicular, respectively, to
parallel and perpendicular, respectively, to  , and
, and 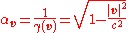 .
.
Einstein's addition of colinear velocities is consistent with the Fizeau experimentFizeau experimentThe Fizeau experiment was carried out by Hippolyte Fizeau in 1851 to measure the relative speeds of light in moving water. Albert Einstein later pointed out the importance of the experiment for special relativity...
which determined the speed of light in a fluid moving parallel to the light, but no experiment has ever tested the formula for the general case of non-parallel velocities.
Relativistic mechanics
In addition to modifying notions of space and time, special relativity forces one to reconsider the concepts of massMassMass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, momentumMomentumIn classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, and energyEnergyIn physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
, all of which are important constructs in Newtonian mechanics. Special relativity shows, in fact, that these concepts are all different aspects of the same physical quantity in much the same way that it shows space and time to be interrelated.
There are a couple of (equivalent) ways to define momentum and energy in SR. One method uses conservation lawConservation lawIn physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
s. If these laws are to remain valid in SR they must be true in every possible reference frame. However, if one does some simple thought experimentThought experimentA thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...
s using the Newtonian definitions of momentum and energy, one sees that these quantities are not conserved in SR. One can rescue the idea of conservation by making some small modifications to the definitions to account for relativistic velocities. It is these new definitions which are taken as the correct ones for momentum and energy in SR.
The energy and momentum of an object with invariant massInvariant massThe invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
m (also called rest mass in the case of a single particle), moving with velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
v with respect to a given frame of reference, are given by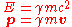
respectively, where γ (the Lorentz factorLorentz factorThe Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
) is given by
The quantity γm is often called the relativistic mass of the object in the given frame of reference,
although recently this concept is falling into disuse, and Lev B. Okun suggested that "this terminology [...] has no rational justification today", and should no longer be taught.
Other physicists, including Wolfgang RindlerWolfgang RindlerWolfgang Rindler is a leading physicist working in the field of General Relativity where he is well known for introducing the term "event horizon", Rindler coordinates, and for popularizing the use of spinors in general relativity. He is also a prolific textbook author.-Education:Rindler gained...
and T. R. Sandin, have argued that relativistic mass is a useful concept and there is little reason to stop using it.
See Mass in special relativityMass in special relativityMass in special relativity incorporates the general understandings from the concept of mass-energy equivalence. Added to this concept is an additional complication resulting from the fact that "mass" is defined in two different ways in special relativity: one way defines mass as an invariant...
for more information on this debate. Some authors use the symbol m to refer to relativistic mass, and the symbol m0 to refer to rest mass.
The energy and momentum of an object with invariant mass m are related by the formulas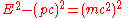
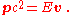
The first is referred to as the relativistic energy-momentum equation. While the energy E and the momentum p depend on the frame of reference in which they are measured, the quantity E2 − (pc)2 is invariant, being equal to the squared invariant mass of the object (up toUp toIn mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
the multiplicative constant c4).
It should be noted that the invariant mass of a system
is greater than the sum of the rest masses of the particles it is composed of (unless they are all stationary with respect to the center of massCenter of massIn physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
of the system, and hence to each other). The sum of rest masses is not even always conserved in isolated systemIsolated systemIn the natural sciences an isolated system, as contrasted with an open system, is a physical system without any external exchange. If it has any surroundings, it does not interact with them. It obeys in particular the first of the conservation laws: its total energy - mass stays constant...
s, since rest mass may be converted to particles which individually have no mass, such as photons. Invariant mass, however, is conserved and invariant for all observers, so long as the system remains isolated (closed to all matter and energy). This is because even massless particles contribute invariant mass to systems, as also does the kinetic energy of particles. Thus, even under transformations of rest mass to photons or kinetic energy, the invariant mass of a system which contains these energies still reflects the invariant mass associated with them.
Mass–energy equivalence
For massless particles, m is zero. The relativistic energy-momentum equation still holds, however, and by substituting m with 0, the relation E = pc is obtained; when substituted into Ev = c2p, it gives v = c: massless particles (such as photons) always travel at the speed of light.
A particle which has no rest mass (for example, a photon) can nevertheless contribute to the total invariant mass of a system, since some or all of its momentum is cancelled by another particle, causing a contribution to the system's invariant mass due to the photon's energy. For single photons this does not happen, since the energy and momentum terms exactly cancel.
Looking at the above formula for invariant mass of a system, one sees that, when a single massive object is at rest (v = 0, p = 0), there is a non-zero mass remaining: mrest = E/c2.
The corresponding energy, which is also the total energy when a single particle is at rest, is referred to as "rest energy". In systems of particles which are seen from a moving inertial frame, total energy increases and so does momentum. However, for single particles the rest mass remains constant, and for systems of particles the invariant mass remain constant, because in both cases, the energy and momentum increases subtract from each other, and cancel. Thus, the invariant mass of systems of particles is a calculated constant for all observers, as is the rest mass of single particles.
The mass of systems and conservation of invariant mass
For systems of particles, the energy-momentum equation requires summing the momentum vectors of the particles:
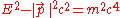
The inertial frame in which the momenta of all particles sums to zero is called the center of momentum frameCenter of momentum frameA center-of-momentum frame of a system is any inertial frame in which the center of mass is at rest . Note that the center of momentum of a system is not a location, but rather defines a particular inertial frame...
. In this special frame, the relativistic energy-momentum equation has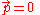 , and thus gives the invariant mass of the system as merely the total energy of all parts of the system, divided by c2
, and thus gives the invariant mass of the system as merely the total energy of all parts of the system, divided by c2
This is the invariant mass of any system which is measured in a frame where it has zero total momentum, such as a bottle of hot gas on a scale. In such a system, the mass which the scale weighs is the invariant mass, and it depends on the total energy of the system. It is thus more than the sum of the rest masses of the molecules, but also includes all the totaled energies in the system as well. Like energy and momentum, the invariant mass of isolated systems cannot be changed so long as the system remains totally closed (no mass or energy allowed in or out), because the total relativistic energy of the system remains constant so long as nothing can enter or leave it.
An increase in the energy of such a system which is caused by translating the system to an inertial frame which is not the center of momentum frameCenter of momentum frameA center-of-momentum frame of a system is any inertial frame in which the center of mass is at rest . Note that the center of momentum of a system is not a location, but rather defines a particular inertial frame...
, causes an increase in energy and momentum without an increase in invariant mass. E = mc2, however, applies only to isolated systems in their center-of-momentum frame where momentum sums to zero.
Taking this formula at face value, we see that in relativity, mass is simply another form of energy. In 1927 Einstein remarked about special relativity, "Under this theory mass is not an unalterable magnitude, but a magnitude dependent on (and, indeed, identical with) the amount of energy."
Einstein was not referring to isolated systems in this remark, however. For, even in his 1905 paper, which first derived the relationship between mass and energy, Einstein showed that the energy of an object had to be increased for its invariant mass (rest mass) to increase. In such cases, the system is not isolated (in Einstein's thought experiment, for example, a mass gives off two photons, which are lost to the object's system).
Closed (isolated) systems
In a "totally-closed" system (i.e., isolated systemIsolated systemIn the natural sciences an isolated system, as contrasted with an open system, is a physical system without any external exchange. If it has any surroundings, it does not interact with them. It obeys in particular the first of the conservation laws: its total energy - mass stays constant...
) the total energy, the total momentum, and hence the total invariant mass are conserved. Einstein's formula for change in mass translates to its simplest ΔE = Δmc2 form, however, only in non-closed systems in which energy is allowed to escape (for example, as heat and light), and thus invariant mass is reduced. Einstein's equation shows that such systems must lose mass, in accordance with the above formula, in proportion to the energy they lose to the surroundings. Conversely, if one can measure the differences in mass between a system before it undergoes a reaction which releases heat and light, and the system after the reaction when heat and light have escaped, one can estimate the amount of energy which escapes the system. In both nuclear and chemical reactions, such energy represents the difference in binding energies of electrons in atoms (for chemistry) or between nucleons in nuclei (in atomic reactions). In both cases, the mass difference between reactants and (cooled) products measures the mass of heat and light which will escape the reaction, and thus (using the equation) give the equivalent energy of heat and light which may be emitted if the reaction proceeds.
In chemistry, the mass differences associated with the emitted energy are around 10-9 of the molecular mass. However, in nuclear reactions the energies are so large that they are associated with mass differences, which can be estimated in advance, if the products and reactants have been weighed (atoms can be weighed indirectly by using atomic masses, which are always the same for each nuclideNuclideA nuclide is an atomic species characterized by the specific constitution of its nucleus, i.e., by its number of protons Z, its number of neutrons N, and its nuclear energy state....
). Thus, Einstein's formula becomes important when one has measured the masses of different atomic nuclei. By looking at the difference in masses, one can predict which nuclei have stored energy that can be released by certain nuclear reactionNuclear reactionIn nuclear physics and nuclear chemistry, a nuclear reaction is semantically considered to be the process in which two nuclei, or else a nucleus of an atom and a subatomic particle from outside the atom, collide to produce products different from the initial particles...
s, providing important information which was useful in the development of nuclear energy and, consequently, the nuclear bomb. Historically, for example, Lise MeitnerLise MeitnerLise Meitner FRS was an Austrian-born, later Swedish, physicist who worked on radioactivity and nuclear physics. Meitner was part of the team that discovered nuclear fission, an achievement for which her colleague Otto Hahn was awarded the Nobel Prize...
was able to use the mass differences in nuclei to estimate that there was enough energy available to make nuclear fission a favorable process. The implications of this special form of Einstein's formula have thus made it one of the most famous equations in all of science.
Because the E = mc2 equation applies only to isolated systems in their center of momentum frameCenter of momentum frameA center-of-momentum frame of a system is any inertial frame in which the center of mass is at rest . Note that the center of momentum of a system is not a location, but rather defines a particular inertial frame...
, it has been popularly misunderstood to mean that mass may be converted to energy, after which the mass disappears. However, popular explanations of the equation as applied to systems include open (non-isolated) systems for which heat and light are allowed to escape, when they otherwise would have contributed to the mass (invariant massInvariant massThe invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
) of the system.
Historically, confusion about mass being "converted" to energy has been aided by confusion between mass and "matterMatterMatter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
", where matter is defined as fermionFermionIn particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
particles. In such a definition, electromagnetic radiation and kinetic energy (or heat) are not considered "matter". In some situations, matter may indeed be converted to non-matter forms of energy (see above), but in all these situations, the matter and non-matter forms of energy still retain their original mass.
For isolated systems (closed to all mass and energy exchange), mass never disappears in the center of momentum frame, because energy cannot disappear. Instead, this equation, in context, means only that when any energy is added to, or escapes from, a system in the center-of-momentum frame, the system will be measured as having gained or lost mass, in proportion to energy added or removed. Thus, in theory, if an atomic bomb were placed in a box strong enough to hold its blast, and detonated upon a scale, the mass of this closed system would not change, and the scale would not move. Only when a transparent "window" was opened in the super-strong plasma-filled box, and light and heat were allowed to escape in a beam, and the bomb components to cool, would the system lose the mass associated with the energy of the blast. In a 21 kiloton bomb, for example, about a gram of light and heat is created. If this heat and light were allowed to escape, the remains of the bomb would lose a gram of mass, as it cooled. In this thought-experiment, the light and heat carry away the gram of mass, and would therefore deposit this gram of mass in the objects that absorb them.
Force
In special relativity, Newton's second law does not hold in its form F = ma, but it does if it is expressed as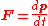
where p is the momentum as defined above (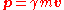 ) and "m" is the invariant massInvariant massThe invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
) and "m" is the invariant massInvariant massThe invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
. Thus, the force is given by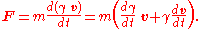
Carrying out the derivatives gives

which, taking into account the identity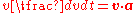 , can also be expressed as
, can also be expressed as
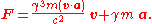
If the acceleration is separated into the part parallel to the velocity and the part perpendicular to it, one gets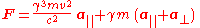
Consequently in some old texts, γ3m is referred to as the longitudinal mass, and γm is referred to as the transverse mass, which is numerically the same as the relativistic mass. See mass in special relativityMass in special relativityMass in special relativity incorporates the general understandings from the concept of mass-energy equivalence. Added to this concept is an additional complication resulting from the fact that "mass" is defined in two different ways in special relativity: one way defines mass as an invariant...
.
For the four-force, see below.
Kinetic energy
The Work-energy Theorem says the change in kinetic energy is equal to the work done on the body, that is
If in the initial state the body was at rest (γ0 = 1) and in the final state it has speed v (γ1 = γ), the kinetic energy is K = (γ − 1)mc2, a result that can be directly obtained by subtracting the rest energy mc2 from the total relativistic energy γmc2.
Classical limit
Notice that γ can be expanded into a Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
or binomial seriesBinomial seriesIn mathematics, the binomial series is the Taylor series at x = 0 of the function f given by f = α, where is an arbitrary complex number...
for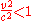 , obtaining:
, obtaining: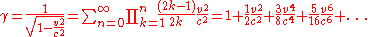
and consequently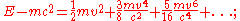

For velocities much smaller than that of light, one can neglect the terms with c2 and higher in the denominator. These formulas then reduce to the standard definitions of Newtonian kinetic energyKinetic energyThe kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
and momentum. This is as it should be, for special relativity must agree with Newtonian mechanics at low velocities.
The geometry of space-time
SR uses a 'flat' 4-dimensional Minkowski space, which is an example of a space-time. This space, however, is very similar to the standard 3 dimensional Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
The differential of distance (ds) in cartesianAnalytic geometryAnalytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
3D space is defined as:
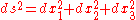
where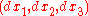 are the differentials of the three spatial dimensions. In the geometry of special relativity, a fourth dimension is added, derived from time, so that the equation for the differential of distance becomes:
are the differentials of the three spatial dimensions. In the geometry of special relativity, a fourth dimension is added, derived from time, so that the equation for the differential of distance becomes:
 .
.
If we wished to make the time coordinate look like the space coordinates, we could treat time as imaginaryImaginary numberAn imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
: x4 = ict (this is called a Wick rotationWick rotationIn physics, Wick rotation, named after Gian-Carlo Wick, is a method of finding a solution to a mathematical problem in Minkowski space from a solution to a related problem in Euclidean space by means of a transformation that substitutes an imaginary-number variable for a real-number variable...
). In this case the above equation becomes symmetric:
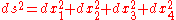 .
.
This suggests what is in fact a profound theoretical insight as it shows that special relativity is simply a rotational symmetryRotational symmetryGenerally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
of our space-time, very similar to rotational symmetry of Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. Just as Euclidean space uses a Euclidean metric, so space-time uses a Minkowski metric. Basically, SR can be stated in terms of the invariance of space-time interval (between any two events) as seen from any inertial reference frame. All equations and effects of special relativity can be derived from this rotational symmetry (the Poincaré groupPoincaré groupIn physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
) of Minkowski space-time. According to Misner (1971 §2.3), ultimately the deeper understanding of both special and general relativity will come from the study of the Minkowski metric (described below) rather than a "disguised" Euclidean metric using ict as the time coordinate.
If we reduce the spatial dimensions to 2, so that we can represent the physics in a 3-D space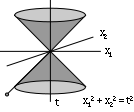
 ,
,
we see that the null geodesicGeodesicIn mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s lie along a dual-cone:
defined by the equation
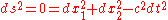
or simply
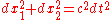 ,
,
which is the equation of a circle of radius c dt.
If we extend this to three spatial dimensions, the null geodesics are the
4-dimensional cone:
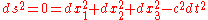
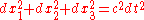 .
.
This null dual-cone represents the "line of sight" of a point in space. That is, when we look at the starStarA star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s and say "The light from that star which I am receiving is X years old", we are looking down this line of sight: a null geodesic. We are looking at an event a distance away and a time d/c in the past. For this reason the null dual cone is also known as the 'light cone'. (The point in the lower left of the picture below represents the star, the origin represents the observer, and the line represents the null geodesic "line of sight".)
away and a time d/c in the past. For this reason the null dual cone is also known as the 'light cone'. (The point in the lower left of the picture below represents the star, the origin represents the observer, and the line represents the null geodesic "line of sight".)
The cone in the -t region is the information that the point is 'receiving', while the cone in the +t section is the information that the point is 'sending'.
The geometry of Minkowski space can be depicted using Minkowski diagramMinkowski diagramThe Minkowski diagram was developed in 1908 by Hermann Minkowski and provides an illustration of the properties of space and time in the special theory of relativity. It allows a quantitative understanding of the corresponding phenomena like time dilation and length contraction without mathematical...
s, which are useful also in understanding many of the thought-experiments in special relativity.
Physics in spacetime
Here, we see how to write the equations of special relativity in a manifestly Lorentz covariantLorentz covarianceIn standard physics, Lorentz symmetry is "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space"...
form. The position of an event in spacetime is given by a contravariant four vector whose components are:

where and
and  and
and  as usual. We define
as usual. We define  so that the time coordinate has the same dimension of distance as the other spatial dimensions; in accordance with the general principle that space and time are treated equally, so far as possible. Superscripts are contravariant indices in this section rather than exponents except when they indicate a square. Subscripts are covariant indices which also range from zero to three as with the spacetime gradient of a field φ:
so that the time coordinate has the same dimension of distance as the other spatial dimensions; in accordance with the general principle that space and time are treated equally, so far as possible. Superscripts are contravariant indices in this section rather than exponents except when they indicate a square. Subscripts are covariant indices which also range from zero to three as with the spacetime gradient of a field φ:
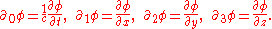
Metric and transformations of coordinates
Having recognised the four-dimensional nature of spacetime, we are driven to employ the Minkowski metric, η, given in components (valid in any inertial reference frame) as:

which is equal to its reciprocal,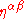 , in those frames.
, in those frames.
Then we recognize that coordinate transformations between inertial reference frames are given by the Lorentz transformationLorentz transformationIn physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
Λ. For the special case of motion along the x-axis, we have:
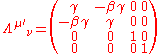
which is simply the matrix of a boost (like a rotation) between the x and ct coordinates. Where μ' indicates the row and ν indicates the column. Also, β and γ are defined as:
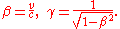
More generally, a transformation from one inertial frame (ignoring translations for simplicity) to another must satisfy:

where there is an implied summation of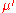 and
and 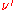 from 0 to 3 on the right-hand side in accordance with the Einstein summation conventionEinstein notationIn mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
from 0 to 3 on the right-hand side in accordance with the Einstein summation conventionEinstein notationIn mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
. The Poincaré groupPoincaré groupIn physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
is the most general group of transformations which preserves the Minkowski metric and this is the physical symmetry underlying special relativity.
All proper physical quantities are given by tensors. So to transform from one frame to another, we use the well-known tensor transformation lawTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
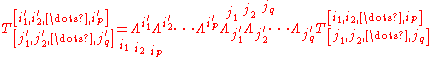
Where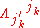 is the reciprocal matrix of
is the reciprocal matrix of 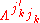 .
.
To see how this is useful, we transform the position of an event from an unprimed coordinate system S to a primed system S, we calculate

which is the Lorentz transformation given above. All tensors transform by the same rule.
The squared length of the differential of the position four-vector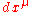 constructed using
constructed using
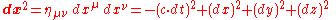
is an invariant. Being invariant means that it takes the same value in all inertial frames, because it is a scalar (0 rank tensor), and so no Λ appears in its trivial transformation. Notice that when the line elementLine elementA line element ds in mathematics can most generally be thought of as the change in a position vector in an affine space expressing the change of the arc length. An easy way of visualizing this relationship is by parametrizing the given curve by Frenet–Serret formulas...
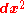 is negative that
is negative that  is the differential of proper timeProper timeIn relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
is the differential of proper timeProper timeIn relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
, while when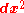 is positive,
is positive,  is differential of the proper distance.
is differential of the proper distance.
The primary value of expressing the equations of physics in a tensor form is that they are then manifestly invariant under the Poincaré group, so that we do not have to do a special and tedious calculation to check that fact. Also in constructing such equations we often find that equations previously thought to be unrelated are, in fact, closely connected being part of the same tensor equation.
Velocity and acceleration in 4D
Recognising other physical quantities as tensors also simplifies their transformation laws. First note that the velocity four-vectorFour-velocityIn physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
Uμ is given by
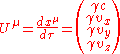
Recognising this, we can turn the awkward looking law about composition of velocities into a simple statement about transforming the velocity four-vector of one particle from one frame to another. Uμ also has an invariant form:
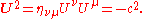
So all velocity four-vectors have a magnitude of c. This is an expression of the fact that there is no such thing as being at coordinate rest in relativity: at the least, you are always moving forward through time. The acceleration 4-vectorFour-accelerationIn special relativity, four-acceleration is a four-vector and is defined as the change in four-velocity over the particle's proper time:whereandand \gamma_u is the Lorentz factor for the speed u...
is given by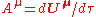 . Given this, differentiating the above equation by τ produces
. Given this, differentiating the above equation by τ produces
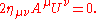
So in relativity, the acceleration four-vector and the velocity four-vector are orthogonal.
Momentum in 4D
The momentum and energy combine into a covariant 4-vector:
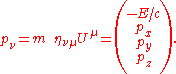
where m is the invariant massInvariant massThe invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
.
The invariant magnitude of the momentum 4-vectorFour-momentumIn special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...
is:

We can work out what this invariant is by first arguing that, since it is a scalar, it doesn't matter which reference frame we calculate it, and then by transforming to a frame where the total momentum is zero.
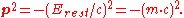
We see that the rest energy is an independent invariant. A rest energy can be calculated even for particles and systems in motion, by translating to a frame in which momentum is zero.
The rest energy is related to the mass according to the celebrated equation discussed above:
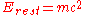
Note that the mass of systems measured in their center of momentum frame (where total momentum is zero) is given by the total energy of the system in this frame. It may not be equal to the sum of individual system masses measured in other frames.
Force in 4D
To use Newton's third law of motion, both forces must be defined as the rate of change of momentum with respect to the same time coordinate. That is, it requires the 3D force defined above. Unfortunately, there is no tensor in 4D which contains the components of the 3D force vector among its components.
If a particle is not traveling at c, one can transform the 3D force from the particle's co-moving reference frame into the observer's reference frame. This yields a 4-vector called the four-force. It is the rate of change of the above energy momentum four-vectorFour-vectorIn the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
with respect to proper time. The covariant version of the four-force is:
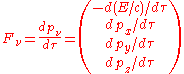
where is the proper time.
is the proper time.
In the rest frame of the object, the time component of the four force is zero unless the "invariant massInvariant massThe invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
" of the object is changing (this requires a non-closed system in which energy/mass is being directly added or removed from the object) in which case it is the negative of that rate of change of mass, times c. In general, though, the components of the four force are not equal to the components of the three-force, because the three force is defined by the rate of change of momentum with respect to coordinate time, i.e.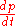 while the four force is defined by the rate of change of momentum with respect to proper time, i.e.
while the four force is defined by the rate of change of momentum with respect to proper time, i.e. 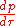 .
.
In a continuous medium, the 3D density of force combines with the density of power to form a covariant 4-vector. The spatial part is the result of dividing the force on a small cell (in 3-space) by the volume of that cell. The time component is −1/c times the power transferred to that cell divided by the volume of the cell. This will be used below in the section on electromagnetism.
Relativity and unifying electromagnetism
Theoretical investigation in classical electromagnetismClassical electromagnetismClassical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
led to the discovery of wave propagation. Equations generalizing the electromagnetic effects found that finite propagation-speed of the E and B fields required certain behaviors on charged particles. The general study of moving charges forms the Liénard–Wiechert potential, which is a step towards special relativity.
The Lorentz transformation of the electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
of a moving charge into a non-moving observer's reference frame results in the appearance of a mathematical term commonly called the magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
. Conversely, the magnetic field generated by a moving charge disappears and becomes a purely electrostatic field in a comoving frame of reference. Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
are thus simply an empirical fit to special relativistic effects in a classical model of the Universe. As electric and magnetic fields are reference frame dependent and thus intertwined, one speaks of electromagnetic fields. Special relativity provides the transformation rules for how an electromagnetic field in one inertial frame appears in another inertial frame.
Electromagnetism in 4D
Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
in the 3D form are already consistent with the physical content of special relativity. But we must rewrite them to make them manifestly invariant.
The charge densityCharge densityThe linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
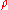 and current densityCurrent densityCurrent density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
and current densityCurrent densityCurrent density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
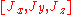 are unified into the current-charge 4-vectorFour-currentIn special and general relativity, the four-current is the Lorentz covariant four-vector that replaces the electromagnetic current density, or indeed any conventional charge current density...
are unified into the current-charge 4-vectorFour-currentIn special and general relativity, the four-current is the Lorentz covariant four-vector that replaces the electromagnetic current density, or indeed any conventional charge current density...
:
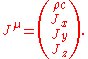
The law of charge conservationCharge conservationIn physics, charge conservation is the principle that electric charge can neither be created nor destroyed. The net quantity of electric charge, the amount of positive charge minus the amount of negative charge in the universe, is always conserved...
, , becomes:
, becomes:
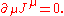
The electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
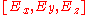 and the magnetic inductionMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
and the magnetic inductionMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
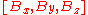 are now unified into the (rank 2 antisymmetric covariant) electromagnetic field tensor:
are now unified into the (rank 2 antisymmetric covariant) electromagnetic field tensor:
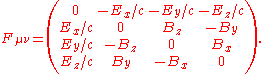
The density, , of the Lorentz forceLorentz forceIn physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
, of the Lorentz forceLorentz forceIn physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
, , exerted on matter by the electromagnetic field becomes:
, exerted on matter by the electromagnetic field becomes:

Faraday's law of inductionFaraday's law of inductionFaraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
,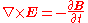 , and Gauss's law for magnetism,
, and Gauss's law for magnetism,  , combine to form:
, combine to form:
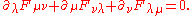
Although there appear to be 64 equations here, it actually reduces to just four independent equations. Using the antisymmetry of the electromagnetic field one can either reduce to an identity (0=0) or render redundant all the equations except for those with λ,μ,ν = either 1,2,3 or 2,3,0 or 3,0,1 or 0,1,2.
The electric displacement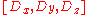 and the magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
and the magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
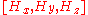 are now unified into the (rank 2 antisymmetric contravariant) electromagnetic displacement tensor:
are now unified into the (rank 2 antisymmetric contravariant) electromagnetic displacement tensor:
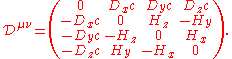
Ampère's law,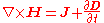 , and Gauss's lawGauss's lawIn physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
, and Gauss's lawGauss's lawIn physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
,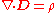 , combine to form:
, combine to form:

In a vacuum, the constitutive equations are:
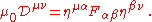
Antisymmetry reduces these 16 equations to just six independent equations. Because it is usual to define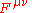 by
by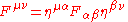
the constitutive equations may, in a vacuum, be combined with Ampère's law etc. to get: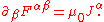
The energy density of the electromagnetic field combines with Poynting vectorPoynting vectorIn physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
and the Maxwell stress tensorMaxwell stress tensorThe Maxwell Stress Tensor is a mathematical object in physics, more precisely it is a second rank tensor used in classical electromagnetism to represent the interaction between electric/magnetic forces and mechanical momentum...
to form the 4D electromagnetic stress-energy tensor. It is the flux (density) of the momentum 4-vector and as a rank 2 mixed tensor it is:

where is the Kronecker delta. When upper index is lowered with η, it becomes symmetric and is part of the source of the gravitational field.
is the Kronecker delta. When upper index is lowered with η, it becomes symmetric and is part of the source of the gravitational field.
The conservation of linear momentum and energy by the electromagnetic field is expressed by:
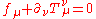
where is again the density of the Lorentz forceLorentz forceIn physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
is again the density of the Lorentz forceLorentz forceIn physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
. This equation can be deduced from the equations above (with considerable effort).
Status
Special relativity in its Minkowski spacetime is accurate only when the absolute value of the gravitational potential is much less than c2 in the region of interest. In a strong gravitational field, one must use general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. General relativity becomes special relativity at the limit of weak field. At very small scales, such as at the Planck length and below, quantum effects must be taken into consideration resulting in quantum gravityQuantum gravityQuantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
. However, at macroscopic scales and in the absence of strong gravitational fields, special relativity is experimentally tested to extremely high degree of accuracy (10−20)
and thus accepted by the physics community. Experimental results which appear to contradict it are not reproducible and are thus widely believed to be due to experimental errors.
Special relativity is mathematically self-consistent, and it is an organic part of all modern physical theories, most notably quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, string theoryString theoryString theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, and general relativity (in the limiting case of negligible gravitational fields).
Newtonian mechanics mathematically follows from special relativity at small velocities (compared to the speed of light) – thus Newtonian mechanics can be considered as a special relativity of slow moving bodies. See Classical mechanicsClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
for a more detailed discussion.
Several experiments predating Einstein's 1905 paper are now interpreted as evidence for relativity. Of these it is known Einstein was aware of the Fizeau experiment before 1905, and historians have concluded that Einstein was at least aware of the Michelson–Morley experiment as early as 1899 despite claims he made in his later years that it played no role in his development of the theory.- The Fizeau experimentFizeau experimentThe Fizeau experiment was carried out by Hippolyte Fizeau in 1851 to measure the relative speeds of light in moving water. Albert Einstein later pointed out the importance of the experiment for special relativity...
(1851, repeated by Michelson and Morley in 1886) measured the speed of light in moving media, with results that are consistent with relativistic addition of colinear velocities. - The famous Michelson–Morley experiment (1881, 1887) gave further support to the postulate that detecting an absolute reference velocity was not achievable. It should be stated here that, contrary to many alternative claims, it said little about the invariance of the speed of light with respect to the source and observer's velocity, as both source and observer were travelling together at the same velocity at all times.
- The Trouton–Noble experiment (1903) showed that the torque on a capacitor is independent of position and inertial reference frame.
- The Experiments of Rayleigh and Brace (1902, 1904) showed that length contraction doesn't lead to birefringence for a co-moving observer, in accordance with the relativity principle.
A number of experiments have been conducted to test special relativity against rival theories. These include:- Kaufmann–Bucherer–Neumann experimentsKaufmann–Bucherer–Neumann experimentsThe Kaufmann-Bucherer-Neumann experiments measured the dependence of the inertial mass of an object on its velocity. The historical importance of a series of this experiment performed by various physicists between 1901 and 1915 is due to the results being used to test the predictions of special...
– electron deflection in approximate agreement with Lorentz-Einstein prediction. - Kennedy–Thorndike experiment – time dilation in accordance with Lorentz transformations
- Rossi-Hall experiment – relativistic effects on a fast-moving particle's half-life
- Experiments to test emission theoryEmission theoryEmission theory was a competing theory for the special theory of relativity, explaining the results of the Michelson-Morley experiment...
demonstrated that the speed of light is independent of the speed of the emitter. - Experiments to test Aether drag hypothesisAether drag hypothesisIn the 19th century, the theory of the luminiferous aether as the hypothetical medium for the propagation of light was widely discussed. An important part of this discussion was the question concerning the state of motion of Earth with respect to this medium. The aether drag hypothesis dealt with...
– no "aether flow obstruction"
In addition, particle accelerators routinely accelerate and measure the properties of particles moving at near the speed of light, where their behavior is completely consistent with relativity theory and inconsistent with the earlier Newtonian mechanics. These machines would simply not work if they were not engineered according to relativistic principles.
Relativistic quantum mechanics
In contrast to General relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, where it is an unsolved question, whether - and if so how - this theory can be merged with quantum physics to a unified theory of quantum gravitation, the tools of special-relativistic quantum theory are well-developed in the form of the Dirac theoryDirac equationThe Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
. Even the early Bohr-Sommerfeld atomic model explained the fine structureFine structureIn atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to first order relativistic corrections.The gross structure of line spectra is the line spectra predicted by non-relativistic electrons with no spin. For a hydrogenic atom, the gross structure energy...
of alkaline atoms by using both special relativity and the preliminary knowledge on quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
of the time.
Paul DiracPaul DiracPaul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
developed a wave equationWave equationThe wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
- the Dirac equation - fully compatible both with special relativity and with the final version of quantum theory existing after 1926. This theory explained not only the intrinsic angular momentum of the electrons called spinSpin (physics)In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
, a property which can only be stated, but not explained by non-relativistic quantum mechanics, but, when properly quantized, led to the prediction of the antiparticleAntiparticleCorresponding to most kinds of particles, there is an associated antiparticle with the same mass and opposite electric charge. For example, the antiparticle of the electron is the positively charged antielectron, or positron, which is produced naturally in certain types of radioactive decay.The...
of the electron, the positronPositronThe positron or antielectron is the antiparticle or the antimatter counterpart of the electron. The positron has an electric charge of +1e, a spin of ½, and has the same mass as an electron...
. Also the fine structure could finally not be explained without special relativity.
On the other hand, the existence of antiparticles makes obvious that one is not dealing with a naive unification of special relativity and quantum mechanics. Instead a theory is necessary, where one is dealing with quantized fieldsQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, and where particles can be created and destroyed, as in quantum electrodynamicsQuantum electrodynamicsQuantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
or quantum chromodynamicsQuantum chromodynamicsIn theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
.
These elements merge together in the standard modelStandard ModelThe Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics, and this theory, the standard theory of relativistic quantized fields, unifying the principles of special relativity and of quantum physics, belongs actually to the most ambitious, and the most active one (see citations in the article "Standard ModelStandard ModelThe Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
").
See also
- People: Hendrik LorentzHendrik LorentzHendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
| Henri PoincaréHenri PoincaréJules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
| Albert EinsteinAlbert EinsteinAlbert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
| Max PlanckMax PlanckMax Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
| Hermann MinkowskiHermann MinkowskiHermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
| Max von LaueMax von LaueMax Theodor Felix von Laue was a German physicist who won the Nobel Prize in Physics in 1914 for his discovery of the diffraction of X-rays by crystals...
| Arnold SommerfeldArnold SommerfeldArnold Johannes Wilhelm Sommerfeld was a German theoretical physicist who pioneered developments in atomic and quantum physics, and also educated and groomed a large number of students for the new era of theoretical physics...
| Max BornMax BornMax Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
| Gustav HerglotzGustav HerglotzGustav Herglotz was a German mathematician. He is best known for his works on the theory of relativity and seismology....
| Richard C. TolmanRichard C. TolmanRichard Chace Tolman was an American mathematical physicist and physical chemist who was an authority on statistical mechanics. He also made important contributions to theoretical cosmology in the years soon after Einstein's discovery of general relativity... - Relativity: Theory of relativityTheory of relativityThe theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
| History of special relativityHistory of special relativityThe history of special relativity consists of many theoretical results and empirical findings obtained by Albert Michelson, Hendrik Lorentz, Henri Poincaré and others...
| principle of relativityPrinciple of relativityIn physics, the principle of relativity is the requirement that the equations describing the laws of physics have the same form in all admissible frames of reference....
| general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
| Fundamental Speed | frame of referenceFrame of referenceA frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
| inertial frame of referenceInertial frame of referenceIn physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
| Lorentz transformations | Bondi k-calculusBondi k-calculusBondi k-calculus is a method of teaching special relativity originated by Professor Sir Hermann Bondi, and now common in university and college level physics classes.The usefulness of the k-calculus is its simplicity...
| Einstein synchronisationEinstein synchronisationEinstein synchronisation is a convention for synchronising clocks at different places by means of signal exchanges. This synchronisation method was used already by telegraphers in the middle 19th century, but was popularized by H. Poincaré and A...
| Rietdijk-Putnam ArgumentRietdijk-Putnam ArgumentIn philosophy, the Rietdijk–Putnam argument, named after C. W. Rietdijk and Hilary Putnam, uses 20th-century findings in physics—specifically in special relativity—to support the philosophical position known as four-dimensionalism....
| Criticism of relativity theoryCriticism of relativity theoryCriticism of Albert Einstein's theory of relativity was mainly expressed in the early years after its publication on a scientific, pseudoscientific, philosophical, or ideological basis. Reasons for criticism were, for example, alternative theories, rejection of the abstract-mathematical method,... - Physics: Newtonian Mechanics | spacetimeSpacetimeIn physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
| speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
| simultaneityRelativity of simultaneityIn physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur...
| physical cosmologyPhysical cosmologyPhysical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
| Doppler effectDoppler effectThe Doppler effect , named after Austrian physicist Christian Doppler who proposed it in 1842 in Prague, is the change in frequency of a wave for an observer moving relative to the source of the wave. It is commonly heard when a vehicle sounding a siren or horn approaches, passes, and recedes from...
| relativistic Euler equationsRelativistic Euler equationsIn fluid mechanics and astrophysics, the relativistic Euler equations are a generalization of the Euler equations that account for the effects of special relativity....
| Aether drag hypothesisAether drag hypothesisIn the 19th century, the theory of the luminiferous aether as the hypothetical medium for the propagation of light was widely discussed. An important part of this discussion was the question concerning the state of motion of Earth with respect to this medium. The aether drag hypothesis dealt with...
| Lorentz ether theoryLorentz ether theoryWhat is now often called Lorentz Ether theory has its roots in Hendrik Lorentz's "Theory of electrons", which was the final point in the development of the classical aether theories at the end of the 19th and at the beginning of the 20th century....
| Moving magnet and conductor problemMoving magnet and conductor problemThe moving magnet and conductor problem is a famous thought experiment, originating in the 19th century, concerning the intersection of classical electromagnetism and special relativity. In it, the current in a conductor moving with constant velocity, v, with respect to a magnet is calculated in...
| Shape wavesShape wavesShape waves are excitations propagating along Josephson vortices or fluxons. In the case of two-dimensional Josephson junctions described by the 2D sine-Gordon equation, shape waves are distortions of a Josephson vortex line of an arbitrary profile...
| Relativistic heat conductionRelativistic heat conductionThe theory of relativistic heat conduction claims to be the only model for heat conduction that is compatible with the theory of special relativity, the second law of thermodynamics, electrodynamics, and quantum mechanics, simultaneously... - Mathematics: Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
| four-vectorFour-vectorIn the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
| world lineWorld lineIn physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
| light coneLight coneA light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
| Lorentz groupLorentz groupIn physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
| Poincaré groupPoincaré groupIn physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
| geometryGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
| tensors | split-complex numberSplit-complex numberIn abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
| Relativity in the APS formalismAlgebra of physical spaceIn physics, the algebra of physical space is the use of the Clifford or geometric algebra Cℓ3 of the three-dimensional Euclidean space as a model for -dimensional space-time, representing a point in space-time via a paravector .The Clifford algebra Cℓ3 has a faithful representation, generated by... - Philosophy: actualismActualismIn contemporary analytic philosophy, actualism is a position on the ontological status of possible worlds that holds that everything that exists is actual. Another phrasing of the thesis is that the domain of unrestricted quantification ranges over all and only actual existents...
| conventionalismConventionalismConventionalism is the philosophical attitude that fundamental principles of a certain kind are grounded on agreements in society, rather than on external reality...
| formalismFormalism (mathematics)In foundations of mathematics, philosophy of mathematics, and philosophy of logic, formalism is a theory that holds that statements of mathematics and logic can be thought of as statements about the consequences of certain string manipulation rules.... - Paradoxes: Twin paradoxTwin paradoxIn physics, the twin paradox is a thought experiment in special relativity, in which a twin makes a journey into space in a high-speed rocket and returns home to find he has aged less than his identical twin who stayed on Earth...
| Ehrenfest paradoxEhrenfest paradoxThe Ehrenfest paradox concerns the rotation of a "rigid" disc in the theory of relativity.In its original formulation as presented by Paul Ehrenfest 1909 in the Physikalische Zeitschrift, it discusses an ideally rigid cylinder that is made to rotate about its axis of symmetry...
| Ladder paradoxLadder paradoxThe ladder paradox is a thought experiment in special relativity. It involves a ladder travelling horizontally and undergoing a length contraction, the result of which being that it can fit into a much smaller garage...
| Bell's spaceship paradoxBell's spaceship paradoxBell's spaceship paradox is a thought experiment in special relativity involving accelerated spaceships and strings. The results of this thought experiment are for many people paradoxical. While J. S. Bell's 1976 version of the paradox is the most widely known, it was first designed by E. Dewan and M...
| Velocity composition paradox
Textbooks
- Einstein, Albert (1920). Relativity: The Special and General Theory.
- Einstein, Albert (1996). The Meaning of Relativity. Fine Communications. ISBN 1-56731-136-9
- Freund, Jűrgen (2008) Special Relativity for Beginners - A Textbook for Undergraduates World Scientific. ISBN 981-277-160-3
- Logunov, Anatoly A. (2005) Henri Poincaré and the Relativity Theory (transl. from Russian by G. Pontocorvo and V. O. Soleviev, edited by V. A. Petrov) Nauka, Moscow.
- Charles Misner, Kip ThorneKip ThorneKip Stephen Thorne is an American theoretical physicist, known for his prolific contributions in gravitation physics and astrophysics and for having trained a generation of scientists...
, and John Archibald WheelerJohn Archibald WheelerJohn Archibald Wheeler was an American theoretical physicist who was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in explaining the basic principles behind nuclear fission...
(1971) Gravitation. W. H. Freeman & Co. ISBN 0-7167-0334-3 - Post, E.J., 1997 (1962) Formal Structure of Electromagnetics: General Covariance and Electromagnetics. Dover Publications.
- Wolfgang RindlerWolfgang RindlerWolfgang Rindler is a leading physicist working in the field of General Relativity where he is well known for introducing the term "event horizon", Rindler coordinates, and for popularizing the use of spinors in general relativity. He is also a prolific textbook author.-Education:Rindler gained...
(1991). Introduction to Special Relativity (2nd ed.), Oxford University Press. ISBN13: 9780198539520; ISBN 0198539525 - Harvey R. Brown (2005). Physical relativity: space-time structure from a dynamical perspective, Oxford University Press, ISBN13: 0-19-927583-1; ISBN 978-0-19-927583-0
- Silberstein, Ludwik (1914) The Theory of Relativity.
- Taylor, Edwin, and John Archibald WheelerJohn Archibald WheelerJohn Archibald Wheeler was an American theoretical physicist who was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in explaining the basic principles behind nuclear fission...
(1992) Spacetime Physics (2nd ed.). W.H. Freeman & Co. ISBN 0-7167-2327-1 - Tipler, Paul, and Llewellyn, Ralph (2002). Modern Physics (4th ed.). W. H. Freeman & Co. ISBN 0-7167-4345-0
External links
Original works
- Zur Elektrodynamik bewegter Körper Einstein's original work in German, Annalen der PhysikAnnalen der PhysikAnnalen der Physik is one of the oldest physics journals worldwide. The journal publishes original, peer-reviewed papers in the areas of experimental, theoretical, applied and mathematical physics and related areas...
, Bern 1905 - On the Electrodynamics of Moving Bodies English Translation as published in the 1923 book The Principle of Relativity.
Special relativity for a general audience (no math knowledge required)
- Wikibooks: Special Relativity
- Einstein Light An award-winning, non-technical introduction (film clips and demonstrations) supported by dozens of pages of further explanations and animations, at levels with or without mathematics.
- Einstein Online Introduction to relativity theory, from the Max Planck Institute for Gravitational Physics.
- Audio: Cain/Gay (2006) - Astronomy Cast. Einstein's Theory of Special Relativity
Special relativity explained (using simple or more advanced math)
- Greg Egan's Foundations.
- The Hogg Notes on Special Relativity A good introduction to special relativity at the undergraduate level, using calculus.
- Motion Mountain, Volume II - A modern introduction to relativity, including its visual effects.
- The Origins of Einstein's Special Theory of Relativity - A historical approach to the study of the special theory of relativity.
- MathPages - Reflections on Relativity A complete online book on relativity with an extensive bibliography.
- Relativity An introduction to special relativity at the undergraduate level, without calculus., by Albert EinsteinAlbert EinsteinAlbert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
- Special Relativity Lecture Notes is a standard introduction to special relativity containing illustrative explanations based on drawings and spacetime diagrams from Virginia Polytechnic Institute and State University.
- Understanding Special Relativity The theory of special relativity in an easily understandable way.
- An Introduction to the Special Theory of Relativity (1964) by Robert Katz, "an introduction ... that is accessible to any student who has had an introduction to general physics and some slight acquaintance with the calculus." (130 pp; pdf format)
- Lecture Notes on Special Relativity by J D Cresser Department of Physics Macquarie University
Visualization
- Raytracing Special Relativity Software visualizing several scenarios under the influence of special relativity.
- Real Time Relativity The Australian National University. Relativistic visual effects experienced through an interactive program.
- Spacetime travel A variety of visualizations of relativistic effects, from relativistic motion to black holes.
- Through Einstein's Eyes The Australian National University. Relativistic visual effects explained with movies and images.
- Warp Special Relativity Simulator A computer program to show the effects of traveling close to the speed of light.
- Animation clip visualizing the Lorentz transformation.
- Original interactive FLASH Animations from John de Pillis illustrating Lorentz and Galilean frames, Train and Tunnel Paradox, the Twin Paradox, Wave Propagation, Clock Synchronization, etc.
- Relativistic Optics at the ANU
-