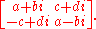Quaternion
Encyclopedia
In mathematics
, the quaternions are a number system
that extends the complex number
s. They were first described by Irish mathematician Sir William Rowan Hamilton
in 1843 and applied to mechanics
in three-dimensional space
. A feature of quaternions is that the product of two quaternions is noncommutative, meaning that the product of two quaternions depends on which factor is to the left of the multiplication sign and which factor is to the right. Hamilton defined a quaternion as the quotient
of two directed lines in a three-dimensional space or equivalently as the quotient of two vectors.
Quaternions can also be represented as the sum of a scalar
and a vector.
Quaternions find uses in both theoretical and applied mathematics, in particular for calculations involving three-dimensional rotations
such as in three-dimensional computer graphics
and computer vision
. They can be used alongside other methods, such as Euler angles
and matrices
, or as an alternative to them depending on the application.
In modern language, quaternions form a four-dimensional associative normed division algebra
over the real number
s, and thus also form a domain
. In fact, the quaternions were the first noncommutative division algebra to be discovered. The algebra of quaternions is often denoted by H (for Hamilton), or in blackboard bold
by (Unicode
(Unicode
U+210D). It can also be given by the Clifford algebra
classifications
. The algebra H holds a special place in analysis since, according to the Frobenius theorem
, it is one of only two finite-dimensional division ring
s containing the real numbers as a proper subring
, the other being the complex numbers.
The unit quaternions can therefore be thought of as a choice of a group structure on the 3-sphere , the group Spin(3), the group SU(2), or the universal cover of SO(3).
, the group Spin(3), the group SU(2), or the universal cover of SO(3).
in 1843. Important precursors to this work included Euler's four-square identity
(1748) and Olinde Rodrigues
' parameterization of general rotations by four parameters (1840), but neither of these writers treated the four-parameter rotations as an algebra. Carl Friedrich Gauss
had also discovered quaternions in 1819, but this work was only published in 1900.
Hamilton knew that the complex number
s could be interpreted as points
in a plane
, and he was looking for a way to do the same for points in three-dimensional space
. Points in space can be represented by their coordinates, which are triples of numbers, and for many years Hamilton had known how to add and subtract triples of numbers. However, Hamilton had been stuck on the problem of multiplication and division for a long time. He could not figure out how to calculate the quotient
of the coordinates of two points in space.
The great breakthrough in quaternions finally came on Monday 16 October 1843 in Dublin, when Hamilton was on his way to the Royal Irish Academy
where he was going to preside at a council meeting. While walking along the towpath of the Royal Canal with his wife, the concepts behind quaternions were taking shape in his mind. When the answer dawned on him, Hamilton could not resist the urge to carve the formula for the quaternions
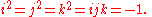
into the stone of Brougham Bridge
as he paused on it.
On the following day, Hamilton wrote a letter to his friend and fellow mathematician, John T. Graves, describing the train of thought that led to his discovery. This letter was later published in the London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, vol. xxv (1844), pp 489–95. On the letter, Hamilton states,
And here there dawned on me the notion that we must admit, in some sense, a fourth dimension of space for the purpose of calculating with triples ... An electric circuit seemed to close, and a spark flashed forth.
Hamilton called a quadruple with these rules of multiplication a quaternion, and he devoted most of the remainder of his life to studying and teaching them. He founded a school of "quaternionists", and he tried to popularize quaternions in several books. The last and longest of his books, Elements of Quaternions, was 800 pages long and was published shortly after his death.
After Hamilton's death, his student Peter Tait
continued promoting quaternions. At this time, quaternions were a mandatory examination topic in Dublin. Topics in physics and geometry that would now be described using vectors, such as kinematics
in space and Maxwell's equations
, were described entirely in terms of quaternions. There was even a professional research association, the Quaternion Society, devoted to the study of quaternions and other hypercomplex number
systems.
From the mid-1880s, quaternions began to be displaced by vector analysis, which had been developed by Josiah Willard Gibbs
, Oliver Heaviside
, and Hermann von Helmholtz
. Vector analysis described the same phenomena as quaternions, so it borrowed some ideas and terminology liberally from the literature of quaternions. However, vector analysis was conceptually simpler and notationally cleaner, and eventually quaternions were relegated to a minor role in mathematics
and physics
. A side-effect of this transition is that Hamilton's work
is difficult to comprehend for many modern readers. Hamilton's original definitions are unfamiliar and his writing style was prolix and opaque.
However, quaternions have had a revival since the late 20th Century
, primarily due to their utility in describing spatial rotations. The representations of rotations by quaternions are more compact and quicker to compute than the representations by matrices. In addition, unlike Euler angles
they are not susceptible to gimbal lock
. For this reason, quaternions are used in computer graphics
, computer vision
, robotics
, control theory
, signal processing
, attitude control, physics
, bioinformatics
, molecular dynamics
, computer simulation
s, and orbital mechanics. For example, it is common for the attitude-control systems of spacecraft to be commanded in terms of quaternions. Quaternions have received another boost from number theory
because of their relationships with the quadratic form
s.
Since 1989, the Department of Mathematics of the National University of Ireland, Maynooth
has organized a pilgrimage, where scientists (including the physicists Murray Gell-Mann
in 2002, Steven Weinberg
in 2005, and the mathematician Andrew Wiles
in 2003) take a walk from Dunsink Observatory
to the Royal Canal bridge where no trace of Hamilton's carving remains, unfortunately.
over the real number
s. H has three operations: addition, scalar multiplication, and quaternion multiplication. The sum of two elements of H is defined to be their sum as elements of R4. Similarly the product of an element of H by a real number is defined to be the same as the product in R4. To define the product of two elements in H requires a choice of basis
for R4. The elements of this basis are customarily denoted as 1, i, j, and k. Every element of H can be uniquely written as a linear combination
of these basis elements, that is, as a1 + bi + cj + dk, where a, b, c, and d are real number
s. The basis element 1 will be the identity element
of H, meaning that multiplication by 1 does nothing, and for this reason, elements of H are usually written a + bi + cj + dk, suppressing the basis element 1. Given this basis, associative
quaternion multiplication is defined by first defining the products of basis elements and then defining all other products using the distributive law.

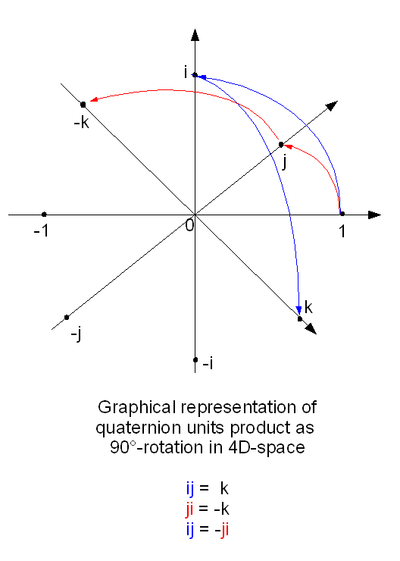
where i, j, and k are basis elements of H, determine all the possible products of i, j, and k. For example, since
right-multiplying both sides by k gives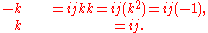
All the other possible products can be determined by similar methods, resulting in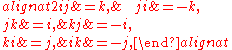
which can be arranged as a table whose rows represent the left factor of the product and whose columns represent the right factor:




Now the basis elements can be multiplied using the rules given above to get:


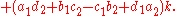
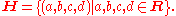
Then the basis elements are:
and the formulas for addition and multiplication are:
and

Hamilton called pure imaginary quaternions right quaternions and real numbers (considered as quaternions with zero vector part) scalar quaternions.
If a quaternion is divided up into a scalar part and a vector part, i.e.

then the formulas for addition and multiplication are:
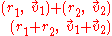
and
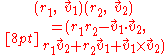
where "" is the dot product
and "" is the cross product
.
 , while
, while  . The noncommutativity of multiplication has some unexpected consequences, among them that polynomial
. The noncommutativity of multiplication has some unexpected consequences, among them that polynomial
equations over the quaternions can have more distinct solutions than the degree of the polynomial. The equation , for instance, has infinitely many quaternion solutions
, for instance, has infinitely many quaternion solutions  with
with  , so that these solutions lie on the two-dimensional surface of a sphere centered on zero in the three-dimensional subspace of quaternions with zero real part. This sphere intersects the complex plane at the two poles
, so that these solutions lie on the two-dimensional surface of a sphere centered on zero in the three-dimensional subspace of quaternions with zero real part. This sphere intersects the complex plane at the two poles  and
and  .
.
The fact that quaternion multiplication is not commutative makes the quaternions an often-cited example of a strictly skew field
.
(5:25–32) published P.R. Girard’s essay The quaternion group and modern physics. It "shows how various physical covariance groups: SO(3), the Lorentz group, the general relativity group, the Clifford algebra SU(2), and the conformal group can be readily related to the quaternion group
" in modern algebra. Girard began by discussing group representation
s and by representing some space group
s of crystallography
. He proceeded to kinematics
of rigid body
motion. Next he used complex quaternions (biquaternions) to represent the Lorentz group
of special relativity, including the Thomas precession
. He cited five authors, beginning with Ludwik Silberstein
who use a potential
function of one quaternion variable
to express Maxwell's equations
in a single differential equation
. Concerning general relativity, he expressed the Runge–Lenz vector. He mentioned the Clifford biquaternions (split-biquaternions) as an instance of Clifford algebra
. Finally, invoking the reciprocal of a biquaternion, Girard described conformal map
s on spacetime
. Among the fifty references, Girard included Alexander Macfarlane
and his Bulletin of the Quaternion Society. In 1999 he showed how Einstein's equations of general relativity could be formulated within a Clifford algebra that is directly linked to quaternions.
A more personal view of quaternions was written by Jim Lambek in 1995. In the Mathematical Intelligencer
(17(4):7) he contributed "If Hamilton Had Prevailed: Quaternions in Physics" which recalled the use of biquaternions: "My own interest as a graduate student was raised by the inspiring book by Silberstein". He concluded by stating "I firmly believe that quaternions can supply a shortcut for pure mathematicians who wish to familiarize themselves with certain aspects of theoretical physics."
In 2007, Alexander P. Yefremov
and co-workers showed that quaternion space geometry is closely linked to the Yang–Mills
field and pointed out connections to the Duffin–Kemmer–Petiau equation and the Klein–Gordon equation.
, which states that every nonnegative integer is the sum of four integer squares. As well as being an elegant theorem in its own right, Lagrange's four square theorem has useful applications in areas of mathematics outside number theory, such as combinatorial design
theory. The quaternion-based proof uses Hurwitz quaternion
s, a subring of the ring of all quaternions for which there is an analog of the Euclidean algorithm
.
s. To define it, let q = a +bi +cj + dk be a quaternion. The conjugate
of q is the quaternion a − bi − cj − dk. It is denoted by q*, , qt, or
, qt, or  . Conjugation is an involution, meaning that it is its own inverse, so conjugating an element twice returns the original element. The conjugate of a product of two quaternions is the product of the conjugates in the reverse order. That is, if p and q are quaternions, then (pq)* = q*p*, not p*q*.
. Conjugation is an involution, meaning that it is its own inverse, so conjugating an element twice returns the original element. The conjugate of a product of two quaternions is the product of the conjugates in the reverse order. That is, if p and q are quaternions, then (pq)* = q*p*, not p*q*.
Unlike the situation in the complex plane,
the conjugation of a quaternion can be expressed entirely with multiplication and addition:
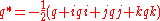
Conjugation can be used to extract the scalar and vector parts of a quaternion. The scalar part of p is (p + p*)/2, and the vector part of p is (p − p*)/2.
The square root of the product of a quaternion with its conjugate is called its norm
and is denoted ||q||. (Hamilton called this quantity the tensor of q, but this conflicts with modern usage. See tensor
.) It has the formula
This is always a non-negative real number, and it is the same as the Euclidean norm on H considered as the vector space R4. Multiplying a quaternion by a real number scales its norm by the absolute value of the number. That is, if α is real, then
This is a special case of the fact that the norm is multiplicative, meaning that
for any two quaternions p and q. Multiplicativity is a consequence of the formula for the conjugate of a product.
Alternatively multiplicativity follows directly from the corresponding property of determinant
s
of square matrices and the formula
where i denotes the usual imaginary unit
.
This norm makes it possible to define the distance d(p, q) between p and q as the norm of their difference:
This makes H into a metric space
. Addition and multiplication are continuous in the metric topology.
A unit quaternion is a quaternion of norm one. Dividing a non-zero quaternion q by its norm produces a unit quaternion Uq called the versor of q:
Every quaternion has a polar decomposition q = ||q|| Uq.
Using conjugation and the norm makes it possible to define the reciprocal
of a quaternion. The product of a quaternion with its reciprocal should equal 1, and the considerations above imply that the product of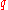 and
and  (in either order) is 1. So the reciprocal of q is defined to be
(in either order) is 1. So the reciprocal of q is defined to be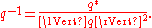
This makes it possible to divide two quaternions p and q in two different ways. That is, their quotient can be either pq−1 or q−1p. The notation is ambiguous because it does not specify whether q divides on the left or the right.
is ambiguous because it does not specify whether q divides on the left or the right.
over the real number
s with dimension 4. (In comparison, the real numbers have dimension 1, the complex numbers have dimension 2, and the octonion
s have dimension 8.) The quaternions have a multiplication that is associative and that distributes over vector addition, but which is not commutative. Therefore the quaternions H are a non-commutative associative algebra
over the real numbers. Even though H contains copies of the complex numbers, it is not an associative algebra over the complex numbers.
Because it is possible to divide quaternions, they form a division algebra
. This is a structure similar to a field
except for the commutativity of multiplication. Finite-dimensional associative division algebras over the real numbers are very rare. The Frobenius theorem
states that there are exactly three: R, C, and H.
The norm makes the quaternions into a normed algebra, and normed division algebras over the reals are also very rare: Hurwitz's theorem says that there are only four: R, C, H, and O (the octonions). The quaternions are also an example of a composition algebra
and of a unital Banach algebra
.
Because the product of any two basis vectors is plus or minus another basis vector, the set {±1, ±i, ±j, ±k} forms a group
under multiplication. This group is called the quaternion group
and is denoted Q8. The real group ring
of Q8 is a ring RQ8 which is also an eight-dimensional vector space over R. It has one basis vector for each element of Q8. The quaternions are the quotient ring
of RQ8 by the ideal
generated by the elements 1 + (−1), i + (−i), j + (−j), and k + (−k). Here the first term in each of the differences is one of the basis elements 1, i, j, and k, and the second term is one of basis elements −1, −i, −j, and −k, not the additive inverses of 1, i, j, and k.
.
For the remainder of this section, i, j, and k will denote both imaginary basis vectors of H and a basis for R3. Notice that replacing i by −i, j by −j, and k by −k sends a vector to its additive inverse, so the additive inverse of a vector is the same as its conjugate as a quaternion. For this reason, conjugation is sometimes called the spatial inverse.
Choose two imaginary quaternions p = b1i + c1j + d1k and q = b2i + c2j + d2k. Their dot product
is
This is equal to the scalar parts of p*q, qp*, pq*, and q*p. (Note that the vector parts of these four products are different.) It also has the formulas
The cross product
of p and q relative to the orientation determined by the ordered basis i, j, and k is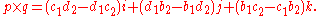
(Recall that the orientation is necessary to determine the sign.) This is equal to the vector part of the product pq (as quaternions), as well as the vector part of −q*p*. It also has the formula
In general, let p and q be quaternions (possibly non-imaginary), and write

where ps and qs are the scalar parts of p and q and and
and  are the vector parts of p and q. Then we have the formula
are the vector parts of p and q. Then we have the formula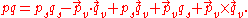
This shows that the noncommutativity of quaternion multiplication comes from the multiplication of pure imaginary quaternions. It also shows that two quaternions commute if and only if their vector parts are collinear.
There are at least two ways of representing quaternions as matrices
in such a way that quaternion addition and multiplication correspond to matrix addition and matrix multiplication
. One is to use 2×2 complex
matrices, and the other is to use 4×4 real
matrices. In the terminology of abstract algebra
, these are injective
homomorphism
s from H to the matrix ring
s M2(C) and M4(R), respectively.
Using 2×2 complex matrices, the quaternion a + bi + cj + dk can be represented as
This representation has the following properties:
Using 4×4 real matrices, that same quaternion can be written as
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the quaternions are a number system
Number system
In mathematics, a 'number system' is a set of numbers, , together with one or more operations, such as addition or multiplication....
that extends the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. They were first described by Irish mathematician Sir William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
in 1843 and applied to mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
in three-dimensional space
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
. A feature of quaternions is that the product of two quaternions is noncommutative, meaning that the product of two quaternions depends on which factor is to the left of the multiplication sign and which factor is to the right. Hamilton defined a quaternion as the quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
of two directed lines in a three-dimensional space or equivalently as the quotient of two vectors.
Quaternions can also be represented as the sum of a scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
and a vector.
Quaternions find uses in both theoretical and applied mathematics, in particular for calculations involving three-dimensional rotations
Quaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
such as in three-dimensional computer graphics
3D computer graphics
3D computer graphics are graphics that use a three-dimensional representation of geometric data that is stored in the computer for the purposes of performing calculations and rendering 2D images...
and computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
. They can be used alongside other methods, such as Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
and matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, or as an alternative to them depending on the application.
In modern language, quaternions form a four-dimensional associative normed division algebra
Normed division algebra
In mathematics, a normed division algebra A is a division algebra over the real or complex numbers which is also a normed vector space, with norm || · || satisfying the following property:\|xy\| = \|x\| \|y\| for all x and y in A....
over the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, and thus also form a domain
Domain (ring theory)
In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
. In fact, the quaternions were the first noncommutative division algebra to be discovered. The algebra of quaternions is often denoted by H (for Hamilton), or in blackboard bold
Blackboard bold
Blackboard bold is a typeface style that is often used for certain symbols in mathematical texts, in which certain lines of the symbol are doubled. The symbols usually denote number sets...
by
 (Unicode
(UnicodeUnicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
U+210D). It can also be given by the Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
classifications
Classification of Clifford algebras
In abstract algebra, in particular in the theory of nondegenerate quadratic forms on vector spaces, the structures of finite-dimensional real and complex Clifford algebras have been completely classified...
. The algebra H holds a special place in analysis since, according to the Frobenius theorem
Frobenius theorem (real division algebras)
In mathematics, more specifically in abstract algebra, the Frobenius theorem, proved by Ferdinand Georg Frobenius in 1877, characterizes the finite-dimensional associative division algebras over the real numbers...
, it is one of only two finite-dimensional division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
s containing the real numbers as a proper subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
, the other being the complex numbers.
The unit quaternions can therefore be thought of as a choice of a group structure on the 3-sphere
 , the group Spin(3), the group SU(2), or the universal cover of SO(3).
, the group Spin(3), the group SU(2), or the universal cover of SO(3).
History
Quaternion algebra was introduced by Irish mathematician Sir William Rowan HamiltonWilliam Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
in 1843. Important precursors to this work included Euler's four-square identity
Euler's four-square identity
In mathematics, Euler's four-square identity says that the product of two numbers, each of which being a sum of four squares, is itself a sum of four squares. Specifically:=\,...
(1748) and Olinde Rodrigues
Olinde Rodrigues
Benjamin Olinde Rodrigues , more commonly known as Olinde Rodrigues, was a French banker, mathematician, and social reformer.Rodrigues was born into a well-to-do Sephardi Jewish family in Bordeaux....
' parameterization of general rotations by four parameters (1840), but neither of these writers treated the four-parameter rotations as an algebra. Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
had also discovered quaternions in 1819, but this work was only published in 1900.
Hamilton knew that the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s could be interpreted as points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
in a plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
, and he was looking for a way to do the same for points in three-dimensional space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
. Points in space can be represented by their coordinates, which are triples of numbers, and for many years Hamilton had known how to add and subtract triples of numbers. However, Hamilton had been stuck on the problem of multiplication and division for a long time. He could not figure out how to calculate the quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
of the coordinates of two points in space.
The great breakthrough in quaternions finally came on Monday 16 October 1843 in Dublin, when Hamilton was on his way to the Royal Irish Academy
Royal Irish Academy
The Royal Irish Academy , based in Dublin, is an all-Ireland, independent, academic body that promotes study and excellence in the sciences, humanities and social sciences. It is one of Ireland's premier learned societies and cultural institutions and currently has around 420 Members, elected in...
where he was going to preside at a council meeting. While walking along the towpath of the Royal Canal with his wife, the concepts behind quaternions were taking shape in his mind. When the answer dawned on him, Hamilton could not resist the urge to carve the formula for the quaternions
into the stone of Brougham Bridge
Broom Bridge
Broom Bridge, also known as Brougham Bridge, is a bridge along Broombridge Road which crosses the Royal Canal in Cabra, Dublin, Ireland. Broom Bridge is named after William Brougham, one of the directors of the Royal Canal company...
as he paused on it.
On the following day, Hamilton wrote a letter to his friend and fellow mathematician, John T. Graves, describing the train of thought that led to his discovery. This letter was later published in the London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, vol. xxv (1844), pp 489–95. On the letter, Hamilton states,
And here there dawned on me the notion that we must admit, in some sense, a fourth dimension of space for the purpose of calculating with triples ... An electric circuit seemed to close, and a spark flashed forth.
Hamilton called a quadruple with these rules of multiplication a quaternion, and he devoted most of the remainder of his life to studying and teaching them. He founded a school of "quaternionists", and he tried to popularize quaternions in several books. The last and longest of his books, Elements of Quaternions, was 800 pages long and was published shortly after his death.
After Hamilton's death, his student Peter Tait
Peter Guthrie Tait
Peter Guthrie Tait FRSE was a Scottish mathematical physicist, best known for the seminal energy physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory, which contributed to the eventual formation of topology as a mathematical...
continued promoting quaternions. At this time, quaternions were a mandatory examination topic in Dublin. Topics in physics and geometry that would now be described using vectors, such as kinematics
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
in space and Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, were described entirely in terms of quaternions. There was even a professional research association, the Quaternion Society, devoted to the study of quaternions and other hypercomplex number
Hypercomplex number
In mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...
systems.
From the mid-1880s, quaternions began to be displaced by vector analysis, which had been developed by Josiah Willard Gibbs
Josiah Willard Gibbs
Josiah Willard Gibbs was an American theoretical physicist, chemist, and mathematician. He devised much of the theoretical foundation for chemical thermodynamics as well as physical chemistry. As a mathematician, he invented vector analysis . Yale University awarded Gibbs the first American Ph.D...
, Oliver Heaviside
Oliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
, and Hermann von Helmholtz
Hermann von Helmholtz
Hermann Ludwig Ferdinand von Helmholtz was a German physician and physicist who made significant contributions to several widely varied areas of modern science...
. Vector analysis described the same phenomena as quaternions, so it borrowed some ideas and terminology liberally from the literature of quaternions. However, vector analysis was conceptually simpler and notationally cleaner, and eventually quaternions were relegated to a minor role in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. A side-effect of this transition is that Hamilton's work
Classical Hamiltonian quaternions
William Rowan Hamilton invented quaternions, a mathematical entity in 1843. This article describes Hamilton's original treatment of quaternions, using his notation and terms. Hamilton's treatment is more geometric than the modern approach, which emphasizes quaternions' algebraic properties...
is difficult to comprehend for many modern readers. Hamilton's original definitions are unfamiliar and his writing style was prolix and opaque.
However, quaternions have had a revival since the late 20th Century
20th century
Many people define the 20th century as running from January 1, 1901 to December 31, 2000, others would rather define it as beginning on January 1, 1900....
, primarily due to their utility in describing spatial rotations. The representations of rotations by quaternions are more compact and quicker to compute than the representations by matrices. In addition, unlike Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
they are not susceptible to gimbal lock
Gimbal lock
Gimbal lock is the loss of one degree of freedom in a three-dimensional space that occurs when the axes of two of the three gimbals are driven into a parallel configuration, "locking" the system into rotation in a degenerate two-dimensional space....
. For this reason, quaternions are used in computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, robotics
Robotics
Robotics is the branch of technology that deals with the design, construction, operation, structural disposition, manufacture and application of robots...
, control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, attitude control, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, bioinformatics
Bioinformatics
Bioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
, molecular dynamics
Molecular dynamics
Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
, computer simulation
Computer simulation
A computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...
s, and orbital mechanics. For example, it is common for the attitude-control systems of spacecraft to be commanded in terms of quaternions. Quaternions have received another boost from number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
because of their relationships with the quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s.
Since 1989, the Department of Mathematics of the National University of Ireland, Maynooth
National University of Ireland, Maynooth
The National University of Ireland, Maynooth , was founded by the Universities Act, 1997 as a constituent university of the National University of Ireland. It is Ireland's second oldest university, having been formed from St Patrick's College, Maynooth, itself founded in 1795.The university is...
has organized a pilgrimage, where scientists (including the physicists Murray Gell-Mann
Murray Gell-Mann
Murray Gell-Mann is an American physicist and linguist who received the 1969 Nobel Prize in physics for his work on the theory of elementary particles...
in 2002, Steven Weinberg
Steven Weinberg
Steven Weinberg is an American theoretical physicist and Nobel laureate in Physics for his contributions with Abdus Salam and Sheldon Glashow to the unification of the weak force and electromagnetic interaction between elementary particles....
in 2005, and the mathematician Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
in 2003) take a walk from Dunsink Observatory
Dunsink Observatory
The Dunsink Observatory is an astronomical observatory established in 1785 in the townland of Dunsink near the city of Dublin, Ireland.Its most famous director was William Rowan Hamilton, who, amongst other things, discovered quaternions, the first non-commutative algebra, while strolling from the...
to the Royal Canal bridge where no trace of Hamilton's carving remains, unfortunately.
Definition
As a set, the quaternions H are equal to R4, a four-dimensional vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. H has three operations: addition, scalar multiplication, and quaternion multiplication. The sum of two elements of H is defined to be their sum as elements of R4. Similarly the product of an element of H by a real number is defined to be the same as the product in R4. To define the product of two elements in H requires a choice of basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for R4. The elements of this basis are customarily denoted as 1, i, j, and k. Every element of H can be uniquely written as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of these basis elements, that is, as a1 + bi + cj + dk, where a, b, c, and d are real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. The basis element 1 will be the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of H, meaning that multiplication by 1 does nothing, and for this reason, elements of H are usually written a + bi + cj + dk, suppressing the basis element 1. Given this basis, associative
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
quaternion multiplication is defined by first defining the products of basis elements and then defining all other products using the distributive law.
Multiplication of basis elements
The equations
where i, j, and k are basis elements of H, determine all the possible products of i, j, and k. For example, since

right-multiplying both sides by k gives
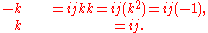
All the other possible products can be determined by similar methods, resulting in
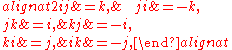
which can be arranged as a table whose rows represent the left factor of the product and whose columns represent the right factor:
| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
Hamilton product
For two elements a1 + b1i + c1j + d1k and a2 + b2i + c2j + d2k, their Hamilton product (a1 + b1i + c1j + d1k)(a2 + b2i + c2j + d2k) is determined by the products of the basis elements and the distributive law. The distributive law makes it possible to expand the product so that it is a sum of products of basis elements. This gives the following expression:



Now the basis elements can be multiplied using the rules given above to get:



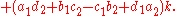
Ordered list form
Using the basis 1, i, j, k of H makes it possible to write H as a set of quadruples: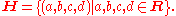
Then the basis elements are:

and the formulas for addition and multiplication are:

and

Scalar and vector parts
A number of the form a + 0i + 0j + 0k, where a is a real number, is called real, and a number of the form 0 + bi + cj + dk, where b, c, and d are real numbers, is called pure imaginary. If a + bi + cj + dk is any quaternion, then a is called its scalar part and bi + cj + dk is called its vector part. The scalar part of a quaternion is always real, and the vector part is always pure imaginary. Even though every quaternion is a vector in a four-dimensional vector space, it is common to define a vector to mean a pure imaginary quaternion. With this convention, a vector is the same as an element of the vector space R3.Hamilton called pure imaginary quaternions right quaternions and real numbers (considered as quaternions with zero vector part) scalar quaternions.
If a quaternion is divided up into a scalar part and a vector part, i.e.

then the formulas for addition and multiplication are:
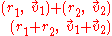
and
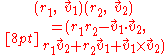
where "" is the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
and "" is the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
.
Noncommutative
Unlike multiplication of real or complex numbers, multiplication of quaternions is not commutative: For example, , while
, while  . The noncommutativity of multiplication has some unexpected consequences, among them that polynomial
. The noncommutativity of multiplication has some unexpected consequences, among them that polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equations over the quaternions can have more distinct solutions than the degree of the polynomial. The equation
 , for instance, has infinitely many quaternion solutions
, for instance, has infinitely many quaternion solutions  with
with  , so that these solutions lie on the two-dimensional surface of a sphere centered on zero in the three-dimensional subspace of quaternions with zero real part. This sphere intersects the complex plane at the two poles
, so that these solutions lie on the two-dimensional surface of a sphere centered on zero in the three-dimensional subspace of quaternions with zero real part. This sphere intersects the complex plane at the two poles 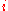 and
and  .
.The fact that quaternion multiplication is not commutative makes the quaternions an often-cited example of a strictly skew field
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
.
Historical impact on physics
In 1984 the European Journal of PhysicsEuropean Journal of Physics
The European Journal of Physics is an international peer-reviewed, scientific journal dedicated to maintaining and improving the standard of physics education in higher education...
(5:25–32) published P.R. Girard’s essay The quaternion group and modern physics. It "shows how various physical covariance groups: SO(3), the Lorentz group, the general relativity group, the Clifford algebra SU(2), and the conformal group can be readily related to the quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
" in modern algebra. Girard began by discussing group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s and by representing some space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
s of crystallography
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
. He proceeded to kinematics
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
of rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
motion. Next he used complex quaternions (biquaternions) to represent the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
of special relativity, including the Thomas precession
Thomas precession
In physics the Thomas precession, named after Llewellyn Thomas, is a special relativistic correction that applies to the spin of an elementary particle or the rotation of a macroscopic gyroscope and relates the angular velocity of the spin of a particle following a curvilinear orbit to the angular...
. He cited five authors, beginning with Ludwik Silberstein
Ludwik Silberstein
Ludwik Silberstein was a Polish-American physicist who helped make special relativity and general relativity staples of university coursework...
who use a potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
function of one quaternion variable
Quaternion variable
In mathematics, a function of a quaternion variable is a function with domain and range in the quaternions H.The projections of a quaternion onto its scalar part or onto its vector part, as well as the modulus and versor functions, are examples that are basic to understanding quaternion structure...
to express Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
in a single differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
. Concerning general relativity, he expressed the Runge–Lenz vector. He mentioned the Clifford biquaternions (split-biquaternions) as an instance of Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
. Finally, invoking the reciprocal of a biquaternion, Girard described conformal map
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
s on spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. Among the fifty references, Girard included Alexander Macfarlane
Alexander Macfarlane (mathematician)
Alexander Macfarlane FRSE was a Scottish logician, physicist, and mathematician.Macfarlane was born in Blairgowrie, Scotland and studied at the University of Edinburgh. His doctoral thesis, on the conditions governing the electric spark, was subsequently published in the Transactions of the Royal...
and his Bulletin of the Quaternion Society. In 1999 he showed how Einstein's equations of general relativity could be formulated within a Clifford algebra that is directly linked to quaternions.
A more personal view of quaternions was written by Jim Lambek in 1995. In the Mathematical Intelligencer
Mathematical Intelligencer
The Mathematical Intelligencer is a mathematical journal published by Springer Verlag that aims at a conversational and scholarly tone, rather than the technical and specialist tone more common amongst such journals.-Mathematical Conversations:...
(17(4):7) he contributed "If Hamilton Had Prevailed: Quaternions in Physics" which recalled the use of biquaternions: "My own interest as a graduate student was raised by the inspiring book by Silberstein". He concluded by stating "I firmly believe that quaternions can supply a shortcut for pure mathematicians who wish to familiarize themselves with certain aspects of theoretical physics."
In 2007, Alexander P. Yefremov
Alexander P. Yefremov
Alexander P. Yefremov is a Russian physicist, vice rector at Peoples' Friendship University of Russia and director of its Institute of Gravitation and Cosmology....
and co-workers showed that quaternion space geometry is closely linked to the Yang–Mills
Yang–Mills
Yang–Mills theory is a gauge theory based on the SU group. Wolfgang Pauli formulated in 1953 the first consistent generalization of the five-dimensional theory of Kaluza, Klein, Fock and others to a higher dimensional internal space...
field and pointed out connections to the Duffin–Kemmer–Petiau equation and the Klein–Gordon equation.
Sums of four squares
Quaternions are also used in one of the proofs of Lagrange's four-square theorem in number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, which states that every nonnegative integer is the sum of four integer squares. As well as being an elegant theorem in its own right, Lagrange's four square theorem has useful applications in areas of mathematics outside number theory, such as combinatorial design
Combinatorial design
Combinatorial design theory is the part of combinatorial mathematics that deals with the existence and construction of systems of finite sets whose intersections have specified numerical properties....
theory. The quaternion-based proof uses Hurwitz quaternion
Hurwitz quaternion
In mathematics, a Hurwitz quaternion is a quaternion whose components are either all integers or all half-integers...
s, a subring of the ring of all quaternions for which there is an analog of the Euclidean algorithm
Euclidean algorithm
In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
.
Conjugation, the norm, and reciprocal
Conjugation of quaternions is analogous to conjugation of complex numbers and to transposition (also known as reversal) of elements of Clifford algebraClifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
s. To define it, let q = a +bi +cj + dk be a quaternion. The conjugate
Conjugate (algebra)
In algebra, a conjugate of an element in a quadratic extension field of a field K is its image under the unique non-identity automorphism of the extended field that fixes K. If the extension is generated by a square root of an element...
of q is the quaternion a − bi − cj − dk. It is denoted by q*,
 , qt, or
, qt, or  . Conjugation is an involution, meaning that it is its own inverse, so conjugating an element twice returns the original element. The conjugate of a product of two quaternions is the product of the conjugates in the reverse order. That is, if p and q are quaternions, then (pq)* = q*p*, not p*q*.
. Conjugation is an involution, meaning that it is its own inverse, so conjugating an element twice returns the original element. The conjugate of a product of two quaternions is the product of the conjugates in the reverse order. That is, if p and q are quaternions, then (pq)* = q*p*, not p*q*.Unlike the situation in the complex plane,
the conjugation of a quaternion can be expressed entirely with multiplication and addition:
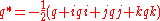
Conjugation can be used to extract the scalar and vector parts of a quaternion. The scalar part of p is (p + p*)/2, and the vector part of p is (p − p*)/2.
The square root of the product of a quaternion with its conjugate is called its norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
and is denoted ||q||. (Hamilton called this quantity the tensor of q, but this conflicts with modern usage. See tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
.) It has the formula

This is always a non-negative real number, and it is the same as the Euclidean norm on H considered as the vector space R4. Multiplying a quaternion by a real number scales its norm by the absolute value of the number. That is, if α is real, then

This is a special case of the fact that the norm is multiplicative, meaning that

for any two quaternions p and q. Multiplicativity is a consequence of the formula for the conjugate of a product.
Alternatively multiplicativity follows directly from the corresponding property of determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s
of square matrices and the formula

where i denotes the usual imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
.
This norm makes it possible to define the distance d(p, q) between p and q as the norm of their difference:

This makes H into a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. Addition and multiplication are continuous in the metric topology.
A unit quaternion is a quaternion of norm one. Dividing a non-zero quaternion q by its norm produces a unit quaternion Uq called the versor of q:

Every quaternion has a polar decomposition q = ||q|| Uq.
Using conjugation and the norm makes it possible to define the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of a quaternion. The product of a quaternion with its reciprocal should equal 1, and the considerations above imply that the product of
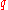 and
and  (in either order) is 1. So the reciprocal of q is defined to be
(in either order) is 1. So the reciprocal of q is defined to be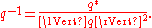
This makes it possible to divide two quaternions p and q in two different ways. That is, their quotient can be either pq−1 or q−1p. The notation
 is ambiguous because it does not specify whether q divides on the left or the right.
is ambiguous because it does not specify whether q divides on the left or the right.Algebraic properties
The set H of all quaternions is a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with dimension 4. (In comparison, the real numbers have dimension 1, the complex numbers have dimension 2, and the octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s have dimension 8.) The quaternions have a multiplication that is associative and that distributes over vector addition, but which is not commutative. Therefore the quaternions H are a non-commutative associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over the real numbers. Even though H contains copies of the complex numbers, it is not an associative algebra over the complex numbers.
Because it is possible to divide quaternions, they form a division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
. This is a structure similar to a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
except for the commutativity of multiplication. Finite-dimensional associative division algebras over the real numbers are very rare. The Frobenius theorem
Frobenius theorem (real division algebras)
In mathematics, more specifically in abstract algebra, the Frobenius theorem, proved by Ferdinand Georg Frobenius in 1877, characterizes the finite-dimensional associative division algebras over the real numbers...
states that there are exactly three: R, C, and H.
The norm makes the quaternions into a normed algebra, and normed division algebras over the reals are also very rare: Hurwitz's theorem says that there are only four: R, C, H, and O (the octonions). The quaternions are also an example of a composition algebra
Composition algebra
In mathematics, a composition algebra A over a field K is a unital algebra over K together with a nondegenerate quadratic form N which satisfiesN = NN\,...
and of a unital Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
.
Because the product of any two basis vectors is plus or minus another basis vector, the set {±1, ±i, ±j, ±k} forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under multiplication. This group is called the quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
and is denoted Q8. The real group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
of Q8 is a ring RQ8 which is also an eight-dimensional vector space over R. It has one basis vector for each element of Q8. The quaternions are the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
of RQ8 by the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by the elements 1 + (−1), i + (−i), j + (−j), and k + (−k). Here the first term in each of the differences is one of the basis elements 1, i, j, and k, and the second term is one of basis elements −1, −i, −j, and −k, not the additive inverses of 1, i, j, and k.
Quaternions and the geometry of R3
Because the vector part of a quaternion is a vector in R3, the geometry of R3 is reflected in the algebraic structure of the quaternions. Many operations on vectors can be defined in terms of quaternions, and this makes it possible to apply quaternion techniques wherever spatial vectors arise. For instance, this is true in electrodynamics and 3D computer graphics3D computer graphics
3D computer graphics are graphics that use a three-dimensional representation of geometric data that is stored in the computer for the purposes of performing calculations and rendering 2D images...
.
For the remainder of this section, i, j, and k will denote both imaginary basis vectors of H and a basis for R3. Notice that replacing i by −i, j by −j, and k by −k sends a vector to its additive inverse, so the additive inverse of a vector is the same as its conjugate as a quaternion. For this reason, conjugation is sometimes called the spatial inverse.
Choose two imaginary quaternions p = b1i + c1j + d1k and q = b2i + c2j + d2k. Their dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
is

This is equal to the scalar parts of p*q, qp*, pq*, and q*p. (Note that the vector parts of these four products are different.) It also has the formulas

The cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of p and q relative to the orientation determined by the ordered basis i, j, and k is
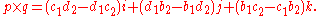
(Recall that the orientation is necessary to determine the sign.) This is equal to the vector part of the product pq (as quaternions), as well as the vector part of −q*p*. It also has the formula

In general, let p and q be quaternions (possibly non-imaginary), and write


where ps and qs are the scalar parts of p and q and
 and
and  are the vector parts of p and q. Then we have the formula
are the vector parts of p and q. Then we have the formula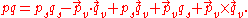
This shows that the noncommutativity of quaternion multiplication comes from the multiplication of pure imaginary quaternions. It also shows that two quaternions commute if and only if their vector parts are collinear.
Matrix representations
Just as complex numbers can be represented as matrices, so can quaternions.There are at least two ways of representing quaternions as matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
in such a way that quaternion addition and multiplication correspond to matrix addition and matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. One is to use 2×2 complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
matrices, and the other is to use 4×4 real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
matrices. In the terminology of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, these are injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s from H to the matrix ring
Matrix ring
In abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
s M2(C) and M4(R), respectively.
Using 2×2 complex matrices, the quaternion a + bi + cj + dk can be represented as
This representation has the following properties:
- Complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s (c = d = 0) correspond to diagonal matrices. - The norm of a quaternion (the square root of a product with its conjugate, as with complex numbers) is the square root of the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the corresponding matrix. - The conjugate of a quaternion corresponds to the conjugate transposeConjugate transposeIn mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of the matrix. - Restricted to unit quaternions, this representation provides an isomorphismGroup isomorphismIn abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
between S33-sphereIn mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
and SU(2). The latter group is important for describing spinSpin (physics)In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
in quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
; see Pauli matricesPauli matricesThe Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
.
Using 4×4 real matrices, that same quaternion can be written as
-

-
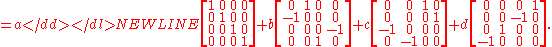
In this representation, the conjugate of a quaternion corresponds to the transposeTransposeIn linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of the matrix. The fourth power of the norm of a quaternion is the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the corresponding matrix. Complex numbers are block diagonal matrices with two 2×2 blocks.
Quaternions as pairs of complex numbers
Quaternions can be represented as pairs of complex numbers. From this perspective, quaternions are the result of applying the Cayley–Dickson construction to the complex numbers. This is a generalization of the construction of the complex numbers as pairs of real numbers.
Let C2 be a two-dimensional vector space over the complex numbers. Choose a basis consisting of two elements 1 and j. A vector in C2 can be written in terms of the basis elements 1 and j as
If we define j2 = −1 and ij = −ji, then we can multiply two vectors using the distributive law. Writing k in place of the product ij leads to the same rules for multiplication as the usual quaternions. Therefore the above vector of complex numbers corresponds to the quaternion a + bi + cj + dk. If we write the elements of C2 as ordered pairs and quaternions as quadruples, then the correspondence is
Square roots of −1
In the complex numbers, there are just two numbers, i and −i, whose square is −1 . In H there are infinitely many square roots of minus one: the quaternion solution for the square root of −1 is the surface of the unit sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
in 3-space. To see this, let q = a + bi + cj + dk be a quaternion, and assume that its square is −1. In terms of a, b, c, and d, this means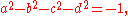



To satisfy the last three equations, either a = 0 or b, c, and d are all 0. The latter is impossible because a is a real number and the first equation would imply that a2 = −1. Therefore a = 0 and b2 + c2 + d2 = 1. In other words, a quaternion squares to −1 if and only if it is a vector (that is, pure imaginary) with norm 1. By definition, the set of all such vectors forms the unit sphere.
Only negative real quaternions have an infinite number of square roots. All others have just two (or one in the case of 0).
The identification of the square roots of minus one in H was given by Hamilton but was frequently omitted in other texts. By 1971 the sphere was included by Sam Perlis in his three page exposition included in Historical Topics in Algebra (page 39) published by the National Council of Teachers of MathematicsNational Council of Teachers of MathematicsThe National Council of Teachers of Mathematics was founded in 1920. It has grown to be the world's largest organization concerned with mathematics education, having close to 100,000 members across the USA and Canada, and internationally....
. More recently, the sphere of square roots of minus one is described in Ian R. PorteousIan R. PorteousIan Robertson Porteous was a Scottish mathematician at the University of Liverpool and an educator on Merseyside. He is best known for three books on geometry and modern algebra...
's book Clifford Algebras and the Classical Groups (Cambridge, 1995) in proposition 8.13 on page 60. Also in Conway (2003) On Quaternions and Octonions we read on page 40: "any imaginary unit may be called i, and perpendicular one j, and their product k", another statement of the sphere.
H as a union of complex planes
Each square root of −1 creates a distinct copy of the complex numbers inside the quaternions. If q2 = −1, then the copy is determined by the function
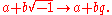
In the language of abstract algebraAbstract algebraAbstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, each is an injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
ring homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
from C to H. The images of the embeddings corresponding to q and -q are identical.
Every non-real quaternion lies in a unique copy of C. Write q as the sum of its scalar part and its vector part:
Decompose the vector part further as the product of its norm and its versor: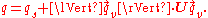
(Note that this is not the same as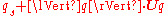 .) The versor of the vector part of q,
.) The versor of the vector part of q, 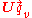 , is a pure imaginary unit quaternion, so its square is −1. Therefore it determines a copy of the complex numbers by the function
, is a pure imaginary unit quaternion, so its square is −1. Therefore it determines a copy of the complex numbers by the function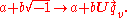
Under this function, q is the image of the complex number .
.
Thus H is the union of complex planes intersecting in a common real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, where the union is taken over the sphere of square roots of minus one.
Commutative subrings
The relationship of quaternions to each other within the complex subplanes of H can also be identified and expressed in terms of commutative subringSubringIn mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
s. Specifically, since two quaternions p and q commute (p q = q p) only if they lie in the same complex subplane of H, the profile of H as a union of complex planes arises when one seeks to find all commutative subringSubringIn mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
s of the quaternion ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. This method of commutative subrings is also used to profile the coquaternionCoquaternionIn abstract algebra, the split-quaternions or coquaternions are elements of a 4-dimensional associative algebra introduced by James Cockle in 1849 under the latter name. Like the quaternions introduced by Hamilton in 1843, they form a four dimensional real vector space equipped with a...
s and 2 × 2 real matrices.
Functions of a quaternion variable
Like functions of a complex variable, functions of a quaternion variable suggest useful physical models. For example, the original electric and magnetic fields described by Maxwell were functions of a quaternion variable.
Exponential, logarithm, and power
The exponentialExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
and logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of a quaternion are relatively inexpensive to compute, particularly compared with the cost of those operations for other charts on SO(3) such as rotation matrices, which require computing the matrix exponentialMatrix exponentialIn mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
and matrix logarithmLogarithm of a matrixIn mathematics, a logarithm of a matrix is another matrix such that the matrix exponential of the latter matrix equals the original matrix. It is thus a generalization of the scalar logarithm and in some sense an inverse function of the matrix exponential. Not all matrices have a logarithm and...
respectively.
Given a quaternion, ,
,
the exponential is computed as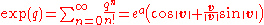
and .
.
It follows that the polar decomposition of a quaternion may be written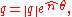
where the angle and the unit vector
and the unit vector  are defined by:
are defined by:
and
Any unit quaternion may be expressed in polar form as .
.
The power of a quaternion raised to an arbitrary (real) exponent is given by:
Three-dimensional and four-dimensional rotation groups
The term "conjugation", besides the meaning given above, can also mean taking an element a to r a r-1 where r is some non-zero element (quaternion). All elements that are conjugate to a given elementConjugacy classIn mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
(in this sense of the word conjugate) have the same real part and the same norm of the vector part. (Thus the conjugate in the other sense is one of the conjugates in this sense.)
Thus the multiplicative group of non-zero quaternions acts by conjugation on the copy of R³ consisting of quaternions with real part equal to zero. Conjugation by a unit quaternion (a quaternion of absolute value 1) with real part cos(θ) is a rotation by an angle 2θ, the axis of the rotation being the direction of the imaginary part. The advantages of quaternions are:
- Non singular representation (compared with Euler anglesEuler anglesThe Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
for example). - More compact (and faster) than matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. - Pairs of unit quaternions represent a rotation in 4D space (see Rotations in 4-dimensional Euclidean space: Algebra of 4D rotations).
The set of all unit quaternions (versors) forms a 3-dimensional sphere3-sphereIn mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
S³ and a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
(a Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
) under multiplication. S³ is the double cover of the group SO(3,R) of real orthogonal 3×3 matricesOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
of determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1 since two unit quaternions correspond to every rotation under the above correspondence.
The image of a subgroup of S³ is a point groupPoint groups in three dimensionsIn geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
, and conversely, the preimage of a point group is a subgroup of S³. The preimage of a finite point group is called by the same name, with the prefix binary. For instance, the preimage of the icosahedral group is the binary icosahedral group.
The group S³ is isomorphic to SU(2), the group of complex unitary 2×2 matrices of determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1.
Let A be the set of quaternions of the form a + bi + cj + dk where a, b, c, and d are either all integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s or all rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s with odd numerator and denominator 2. The set A is a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
(in fact a domainDomain (ring theory)In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
) and a latticeLattice (group)In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
and is called the ring of Hurwitz quaternionHurwitz quaternionIn mathematics, a Hurwitz quaternion is a quaternion whose components are either all integers or all half-integers...
s. There are 24 unit quaternions in this ring, and they are the vertices of a 24-cell regular polytope with Schläfli symbol {3,4,3}.
Generalizations
If F is any fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
with characteristic different from 2, and a and b are elements of F, one may define a four-dimensional unitary associative algebraAssociative algebraIn mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over F with basis 1, i, j, and ij, where i2 = a, j2 = b and ij = −ji (so ij2 = −ab). These algebras are called quaternion algebras and are isomorphic to the algebra of 2×2 matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
over F or form division algebraDivision algebraIn the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
s over F, depending on
the choice of a and b.
Quaternions as the even part of Cℓ3,0(R)
The usefulness of quaternions for geometrical computations can be generalised to other dimensions, by identifying the quaternions as the even part Cℓ+3,0(R) of the Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
Cℓ3,0(R). This is an associative multivector algebra built up from fundamental basis elements σ1, σ2, σ3 using the product rules

If these fundamental basis elements are taken to represent vectors in 3D space, then it turns out that the reflection of a vector r in a plane perpendicular to a unit vector w can be written:
Two reflections make a rotation by an angle twice the angle between the two reflection planes, so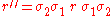
corresponds to a rotation of 180° in the plane containing σ1 and σ2. This is very similar to the corresponding quaternion formula,
In fact, the two are identical, if we make the identification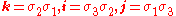
and it is straightforward to confirm that this preserves the Hamilton relations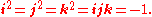
In this picture, quaternions correspond not to vectors but to bivectorBivectorIn mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s, quantities with magnitude and orientations associated with particular 2D planes rather than 1D directions. The relation to complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s becomes clearer, too: in 2D, with two vector directions σ1 and σ2, there is only one bivector basis element σ1σ2, so only one imaginary. But in 3D, with three vector directions, there are three bivector basis elements σ1σ2, σ2σ3, σ3σ1, so three imaginaries.
This reasoning extends further. In the Clifford algebra Cℓ4,0(R), there are six bivector basis elements, since with four different basic vector directions, six different pairs and therefore six different linearly independent planes can be defined. Rotations in such spaces using these generalisations of quaternions, called rotorsRotor (mathematics)A rotor is an n-blade object in geometric algebra, which rotates another n-blade object about a fixed or translated point. They are normally motivated by considering an even number of reflections, which generate rotations...
, can be very useful for applications involving homogeneous coordinatesHomogeneous coordinatesIn mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
. But it is only in 3D that the number of basis bivectors equals the number of basis vectors, and each bivector can be identified as a pseudovectorPseudovectorIn physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...
.
Dorst et al. identify the following advantages for placing quaternions in this wider setting:- Rotors are natural and non-mysterious in geometric algebra and easily understood as the encoding of a double reflection.
- In geometric algebra, a rotor and the objects it acts on live in the same space. This eliminates the need to change representations and to encode new data structures and methods (which is required when augmenting linear algebra with quaternions).
- A rotor is universally applicable to any element of the algebra, not just vectors and other quaternions, but also lines, planes, circles, spheres, rays, and so on.
- In the conformalConformal geometryIn mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
model of Euclidean geometry, rotors allow the encoding of rotation, translation and scaling in a single element of the algebra, universally acting on any element. In particular, this means that rotors can represent rotations around an arbitrary axis, whereas quaternions are limited to an axis through the origin. - Rotor-encoded transformations make interpolation particularly straightforward.
For further detail about the geometrical uses of Clifford algebras, see Geometric algebraGeometric algebraGeometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
.
Brauer group
The quaternions are "essentially" the only (non-trivial) central simple algebraCentral simple algebraIn ring theory and related areas of mathematics a central simple algebra over a field K is a finite-dimensional associative algebra A, which is simple, and for which the center is exactly K...
(CSA) over the real numbers, in the sense that every CSA over the reals is Brauer equivalent to either the reals or the quaternions. Explicitly, the Brauer groupBrauer groupIn mathematics, the Brauer group of a field K is an abelian group whose elements are Morita equivalence classes of central simple algebras of finite rank over K and addition is induced by the tensor product of algebras. It arose out of attempts to classify division algebras over a field and is...
of the reals consists of two classes, represented by the reals and the quaternions, where the Brauer group is the set of all CSAs, up to equivalence relation of one CSA being a matrix ringMatrix ringIn abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
over another. By the Artin–Wedderburn theoremArtin–Wedderburn theoremIn abstract algebra, the Artin–Wedderburn theorem is a classification theorem for semisimple rings. The theorem states that an Artinian semisimple ring R is isomorphic to a product of finitely many ni-by-ni matrix rings over division rings Di, for some integers ni, both of which are uniquely...
(specifically, Wedderburn's part), CSAs are all matrix algebras over a division algebra, and thus the quaternions are the only non-trivial division algebra over the reals.
CSAs – rings over a field, which are simple algebras (have no non-trivial 2-sided ideals, just as with fields) whose center is exactly the field – are a noncommutative analog of extension fields, and are more restrictive than general ring extensions. The fact that the quaternions are the only non-trivial CSA over the reals (up to equivalence) may be compared with the fact that the complex numbers are the only non-trivial field extension of the reals.
Quotes
- "I regard it as an inelegance, or imperfection, in quaternions, or rather in the state to which it has been hitherto unfolded, whenever it becomes or seems to become necessary to have recourse to x, y, z, etc." — William Rowan Hamilton (ed. Quoted in a letter from Tait to Cayley).
- "Time is said to have only one dimension, and space to have three dimensions. […] The mathematical quaternion partakes of both these elements; in technical language it may be said to be "time plus space", or "space plus time": and in this sense it has, or at least involves a reference to, four dimensions. And how the One of Time, of Space the Three, Might in the Chain of Symbols girdled be." — William Rowan Hamilton (Quoted in R.P. Graves, "Life of Sir William Rowan Hamilton").
- "Quaternions came from Hamilton after his really good work had been done; and, though beautifully ingenious, have been an unmixed evil to those who have touched them in any way, including Clerk MaxwellJames Clerk MaxwellJames Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
." — Lord Kelvin, 1892. - "Neither matrices nor quaternions and ordinary vectors were banished from these ten [additional] chapters. For, in spite of the uncontested power of the modern Tensor Calculus, those older mathematical languages continue, in my opinion, to offer conspicuous advantages in the restricted field of special relativity. Moreover, in science as well as in every-day life, the mastery of more than one language is also precious, as it broadens our views, is conducive to criticism with regard to, and guards against hypostasy [weak-foundation] of, the matter expressed by words or mathematical symbols." — Ludwik SilbersteinLudwik SilbersteinLudwik Silberstein was a Polish-American physicist who helped make special relativity and general relativity staples of university coursework...
, preparing the second edition of his Theory of Relativity in 1924. - "… quaternions appear to exude an air of nineteenth century decayDecadenceDecadence can refer to a personal trait, or to the state of a society . Used to describe a person's lifestyle. Concise Oxford Dictionary: "a luxurious self-indulgence"...
, as a rather unsuccessful speciesSpeciesIn biology, a species is one of the basic units of biological classification and a taxonomic rank. A species is often defined as a group of organisms capable of interbreeding and producing fertile offspring. While in many cases this definition is adequate, more precise or differing measures are...
in the struggle-for-lifeSurvival of the fittest"Survival of the fittest" is a phrase originating in evolutionary theory, as an alternative description of Natural selection. The phrase is today commonly used in contexts that are incompatible with the original meaning as intended by its first two proponents: British polymath philosopher Herbert...
of mathematical ideas. Mathematicians, admittedly, still keep a warm place in their hearts for the remarkable algebraic properties of quaternions but, alas, such enthusiasm means little to the harder-headed physical scientist." — Simon L. Altmann, 1986. - "...the thing about a Quaternion 'is' is that we're obliged to encounter it in more than one guise. As a vector quotient. As a way of plotting complex numbers along three axes instead of two. As a list of instructions for turning one vector into another..... And considered subjectively, as an act of becoming longer or shorter, while at the same time turning, among axes whose unit vector is not the familiar and comforting 'one' but the altogether disquieting square root of minus one. If you were a vector, mademoiselle, you would begin in the 'real' world, change your length, enter an 'imaginary' reference system, rotate up to three different ways, and return to 'reality' a new person. Or vector..." — Thomas PynchonThomas PynchonThomas Ruggles Pynchon, Jr. is an American novelist. For his most praised novel, Gravity's Rainbow, Pynchon received the National Book Award, and is regularly cited as a contender for the Nobel Prize in Literature...
, Against the DayAgainst the DayAgainst the Day is a novel by Thomas Pynchon. The narrative takes place between the 1893 Chicago World's Fair and the time immediately following World War I and features more than a hundred characters spread across the United States, Europe, Mexico, Central Asia, and "one or two places not strictly...
, 2006.
Books and publications
- Hamilton, William RowanWilliam Rowan HamiltonSir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
. On quaternions, or on a new system of imaginaries in algebra. Philosophical Magazine. Vol. 25, n 3. p. 489–495. 1844. - Hamilton, William RowanWilliam Rowan HamiltonSir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
(1853), "Lectures on Quaternions". Royal Irish Academy. - Hamilton (1866) Elements of Quaternions University of DublinUniversity of DublinThe University of Dublin , corporately designated the Chancellor, Doctors and Masters of the University of Dublin , located in Dublin, Ireland, was effectively founded when in 1592 Queen Elizabeth I issued a charter for Trinity College, Dublin, as "the mother of a university" – this date making it...
Press. Edited by William Edwin Hamilton, son of the deceased author. - Hamilton (1899) Elements of Quaternions volume I, (1901) volume II. Edited by Charles Jasper JolyCharles Jasper JolyCharles Jasper Joly was an Irish mathematician and astronomer who became Royal Astronomer of Ireland.-Life:...
; published by Longmans, Green & Co.. - Tait, Peter GuthriePeter Guthrie TaitPeter Guthrie Tait FRSE was a Scottish mathematical physicist, best known for the seminal energy physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory, which contributed to the eventual formation of topology as a mathematical...
(1873), "An elementary treatise on quaternions". 2d ed., Cambridge, [Eng.] : The University Press. - Michiel Hazewinkel, Nadiya Gubareni, Nadezhda Mikhaĭlovna Gubareni, Vladimir V. Kirichenko. Algebras, rings and modules. Volume 1. 2004. Springer, 2004. ISBN 1-4020-2690-0
- Maxwell, James Clerk (1873), "A Treatise on Electricity and MagnetismA Treatise on Electricity and MagnetismA Treatise on Electricity and Magnetism is a two volume treatise on electromagnetism written by James Clerk Maxwell in 1873.-See also:* On Physical Lines of Force* A Dynamical Theory of the Electromagnetic Field-External links:...
". Clarendon Press, Oxford. - Tait, Peter GuthriePeter Guthrie TaitPeter Guthrie Tait FRSE was a Scottish mathematical physicist, best known for the seminal energy physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory, which contributed to the eventual formation of topology as a mathematical...
(1886), "Quaternion". M.A. Sec. R.S.E. Encyclopaedia Britannica, Ninth Edition, 1886, Vol. XX, pp. 160–164. (bzipped PostScriptPostScriptPostScript is a dynamically typed concatenative programming language created by John Warnock and Charles Geschke in 1982. It is best known for its use as a page description language in the electronic and desktop publishing areas. Adobe PostScript 3 is also the worldwide printing and imaging...
file) - Joly, Charles Jasper (1905), "A manual of quaternions". London, Macmillan and co., limited; New York, The Macmillan company. LCCN 05036137 //r84
- Macfarlane, AlexanderAlexander MacfarlaneAlexander Macfarlane was a Nova Scotia lawyer and political figure. He was a member of the Canadian Senate from 1870 to 1898. His surname also appears as McFarlane in some sources....
(1906), "Vector analysis and quaternions", 4th ed. 1st thousand. New York, J. Wiley & Sons; [etc., etc.]. LCCN es 16000048 - 1911 encyclopedia: "Quaternions".
- Finkelstein, David, Josef M. Jauch, Samuel Schiminovich, and David Speiser (1962), "Foundations of quaternion quantum mechanics". J. Mathematical Phys. 3, pp. 207–220, MathSciNet.
- Du Val, PatrickPatrick du ValPatrick du Val was a British mathematician, known for his work on algebraic geometry, differential geometry, and general relativity. The concept of Du Val singularity of an algebraic surface is named after him....
(1964), "Homographies, quaternions, and rotations". Oxford, Clarendon Press (Oxford mathematical monographs). LCCN 64056979 //r81 - Crowe, Michael J. (1967), A History of Vector AnalysisA History of Vector AnalysisA History of Vector Analysis is a book on the history of vector analysis by Michael J. Crowe, originally published by the University of Notre Dame Press....
: The Evolution of the Idea of a Vectorial System, University of Notre Dame Press. Surveys the major and minor vector systems of the 19th century (Hamilton, Möbius, Bellavitis, Clifford, Grassmann, Tait, Peirce, Maxwell, Macfarlane, MacAuley, Gibbs, Heaviside). - Altmann, Simon L. (1986), "Rotations, quaternions, and double groups". Oxford [Oxfordshire] : Clarendon Press ; New York : Oxford University Press. LCCN 85013615 ISBN 0-19-855372-2
- Altmann, Simon L. (1989), "Hamilton, Rodrigues, and the Quaternion Scandal". Mathematics Magazine. Vol. 62, No. 5. p. 291–308, Dec. 1989.
- Adler, Stephen L. (1995), "Quaternionic quantum mechanics and quantum fields". New York : Oxford University Press. International series of monographs on physics (Oxford, England) 88. LCCN 94006306 ISBN 0-19-506643-X
- Trifonov, Vladimir (1995), "A Linear Solution of the Four-Dimensionality Problem", Europhysics Letters, 32 (8) 621–626, DOI: 10.1209/0295-5075/32/8/001
- Ward, J. P. (1997), "Quaternions and Cayley Numbers: Algebra and Applications", Kluwer Academic Publishers. ISBN 0-7923-4513-4
- Kantor, I. L. and Solodnikov, A. S. (1989), "Hypercomplex numbers, an elementary introduction to algebras", Springer-Verlag, New York, ISBN 0-387-96980-2
- Gürlebeck, Klaus and Sprössig, Wolfgang (1997), "Quaternionic and Clifford calculus for physicists and engineers". Chichester ; New York : Wiley (Mathematical methods in practice; v. 1). LCCN 98169958 ISBN 0-471-96200-7
- Kuipers, Jack (2002), "Quaternions and Rotation Sequences: A Primer With Applications to Orbits, Aerospace, and Virtual Reality" (reprint edition), Princeton University PressPrinceton University Press-Further reading:* "". Artforum International, 2005.-External links:* * * * *...
. ISBN 0-691-10298-8 - Conway, John HortonJohn Horton ConwayJohn Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
, and Smith, Derek A. (2003), "On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry", A. K. Peters, Ltd. ISBN 1-56881-134-9 (review). - Kravchenko, Vladislav (2003), "Applied Quaternionic Analysis", Heldermann Verlag ISBN 3-88538-228-8.
- Hanson, Andrew J. (2006), "Visualizing Quaternions", Elsevier: Morgan Kaufmann; San Francisco. ISBN 0-12-088400-3
- Trifonov, Vladimir (2007), "Natural Geometry of Nonzero Quaternions", International Journal of Theoretical Physics, 46 (2) 251–257, DOI: 10.1007/s10773-006-9234-9
- Ernst Binz & Sonja Pods (2008) Geometry of Heisenberg Groups American Mathematical SocietyAmerican Mathematical SocietyThe American Mathematical Society is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, which it does with various publications and conferences as well as annual monetary awards and prizes to mathematicians.The society is one of the...
, Chapter 1: "The Skew Field of Quaternions" (23 pages) ISBN 978-0-8218-4495-3. - Vince, John A. (2008), Geometric Algebra for Computer Graphics, Springer, ISBN 978-1-84628-996-5.
- For molecules that can be regarded as classical rigid bodies molecular dynamicsMolecular dynamicsMolecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
computer simulation employs quaternions. They were first introduced for this purpose by D.J. Evans, (1977), "On the Representation of Orientation Space", Mol. Phys., vol 34, p 317.
Links and monographs
- Matrix and Quaternion FAQ v1.21 Frequently Asked Questions
- "Geometric Tools documentation" (frame; body) includes several papers focusing on computer graphics applications of quaternions. Covers useful techniques such as spherical linear interpolation.
- Patrick-Gilles Maillot Provides free Fortran and C source code for manipulating quaternions and rotations / position in space. Also includes mathematical background on quaternions.
- "Geometric Tools source code" (frame; body) includes free C++ source code for a complete quaternion class suitable for computer graphics work, under a very liberal license.
- Doug Sweetser, Doing Physics with Quaternions
- Quaternions for Computer Graphics and Mechanics (Gernot Hoffman)
- The Physical Heritage of Sir W. R. Hamilton (PDF)
- D. R. Wilkins, Hamilton’s Research on Quaternions
- Quaternion Julia Fractals 3D Raytraced Quaternion Julia FractalsJulia setIn the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
by David J. Grossman - Quaternion Math and Conversions Great page explaining basic math with links to straight forward rotation conversion formulae.
- John H. Mathews, Bibliography for Quaternions.
- Quaternion powers on GameDev.net
- Andrew Hanson, Visualizing Quaternions home page.
- Representing Attitude with Euler Angles and Quaternions: A Reference, Technical report and Matlab toolbox summarizing all common attitude representations, with detailed equations and discussion on features of various methods.
- Charles F. F. Karney, Quaternions in molecular modeling, J. Mol. Graph. Mod. 25(5), 595–604 (Jan. 2007); DOI: 10.1016/j.jmgm.2006.04.002; E-print arxiv:0506177.
- Johan E. Mebius, A matrix-based proof of the quaternion representation theorem for four-dimensional rotations., arXiv General Mathematics 2005.
- Johan E. Mebius, Derivation of the Euler-Rodrigues formula for three-dimensional rotations from the general formula for four-dimensional rotations., arXiv General Mathematics 2007.
- NUI Maynooth Department of Mathematics, Hamilton Walk.
- OpenGL:Tutorials:Using Quaternions to represent rotation
- David Erickson, Defence Research and Development CanadaDefence Research and Development CanadaDefence Research and Development Canada, also Defence R&D Canada or DRDC , is an agency of the Department of National Defence , whose purpose is to respond to the scientific and technological needs of the Canadian Forces...
(DRDC), Complete derivation of rotation matrix from unitary quaternion representation in DRDC TR 2005-228 paper. Drdc-rddc.gc.ca - Alberto Martinez, University of Texas Department of History, "Negative Math, How Mathematical Rules Can Be Positively Bent",Utexas.edu
- D. Stahlke, Quaternions in Classical Mechanics Stahlke.org (PDF)
- Morier-Genoud, Sophie, and Valentin Ovsienko. "Well, Papa, can you multiply triplets?", arxiv.org describes how the quaternions can be made into a skew-commutative algebra graded by Z/2×Z/2×Z/2.
- Curious Quaternions by Helen Joyce hosted by John Baez.
Software
- Quaternion Calculator [javascript], bluetulip.org
- Quaternion Calculator [Java], theworld.com
- Quaternion Toolbox for Matlab, qtfm.sourceforge.net
- Boost library support for Quaternions in C++, boost.org
- Mathematics of flight simulation >Turbo-PASCAL software for quaternions, Euler angles and Extended Euler angles, xs4all.nl
- Non singular representation (compared with Euler angles
-