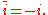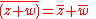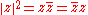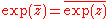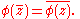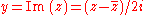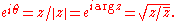Complex conjugate
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, complex conjugates are a pair of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, both having the same real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
part, but with imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
parts of equal magnitude and opposite sign
Sign (mathematics)
In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...
s. For example, 3 + 4i and 3 − 4i are complex conjugates.
The conjugate of the complex number


where
 and
and  are real number
are real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, is

For example,
An alternative notation for the complex conjugate is
 . However, the
. However, the 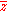 notation avoids confusion with the notation for the conjugate transpose
notation avoids confusion with the notation for the conjugate transposeConjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, which can be thought of as a generalization of complex conjugation. The star-notation is preferred in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
while the bar-notation is more common in pure mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. If a complex number is represented as a 2×2 matrix, the notations are identical.
Complex numbers are considered points in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, a variation of the Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
where both axes are real number lines that cross at the origin, however, the
 -axis is a product of real numbers multiplied by +/-
-axis is a product of real numbers multiplied by +/- 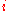 . On the illustration, the
. On the illustration, the  -axis is called the real axis, labeled Re, while the
-axis is called the real axis, labeled Re, while the 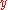 -axis is called the imaginary axis, labeled Im. The plane defined by the Re and Im axes represents the space of all possible complex numbers. In this view, complex conjugation corresponds to reflection of a complex number at the x-axis, equivalent to a
-axis is called the imaginary axis, labeled Im. The plane defined by the Re and Im axes represents the space of all possible complex numbers. In this view, complex conjugation corresponds to reflection of a complex number at the x-axis, equivalent to a  degree rotation of the complex plane about the Re axis.
degree rotation of the complex plane about the Re axis.In polar form, the conjugate of
 is
is 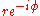 . This can be shown using Euler's formula
. This can be shown using Euler's formulaEuler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
Pairs of complex conjugates are significant because the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
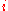 is qualitatively indistinct from its additive and multiplicative inverse
is qualitatively indistinct from its additive and multiplicative inverse  , as they both satisfy the definition for the imaginary unit:
, as they both satisfy the definition for the imaginary unit:  . Thus in most "natural" settings, if a complex number provides a solution to a problem, so does its conjugate, such as is the case for complex solutions of the quadratic formula with real coefficients.
. Thus in most "natural" settings, if a complex number provides a solution to a problem, so does its conjugate, such as is the case for complex solutions of the quadratic formula with real coefficients.Properties
These properties apply for all complex numbers z and w, unless stated otherwise, and can be easily proven by writing z and w in the form a + ib.-
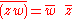 (note the reversed arguments if z and w don't commute)
(note the reversed arguments if z and w don't commute)
-
 if and only if z is real
if and only if z is real
-
 for any integer n
for any integer n
-
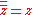 , involution (i.e., the conjugate of the conjugate of a complex number z is again that number)
, involution (i.e., the conjugate of the conjugate of a complex number z is again that number)
-
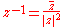 if z is non-zero
if z is non-zero
The latter formula is the method of choice to compute the inverse of a complex number if it is given in rectangular coordinates.
-
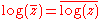 if z is non-zero
if z is non-zero
In general, if
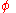 is a holomorphic function
is a holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
whose restriction to the real numbers is real-valued, and
 is defined, then
is defined, thenConsequently, if
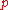 is a polynomial
is a polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
coefficients, and
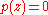 , then
, then 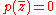 as well. Thus, non-real roots of real polynomials occur in complex conjugate pairs (see Complex conjugate root theorem
as well. Thus, non-real roots of real polynomials occur in complex conjugate pairs (see Complex conjugate root theoremComplex conjugate root theorem
In mathematics, the complex conjugate root theorem states that if P is a polynomial in one variable with real coefficients, and a + bi is a root of P with a and b real numbers, then its complex conjugate a − bi is also a root of P.It follows from this , that if the degree...
).
The map
 from
from  to
to  is a homeomorphism
is a homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
(where the topology on
 is taken to be the standard topology) and antilinear, if one considers
is taken to be the standard topology) and antilinear, if one considers  as a complex vector space
as a complex vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over itself. Even though it appears to be a well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
function, it is not holomorphic; it reverses orientation whereas holomorphic functions locally preserve orientation. It is bijective and compatible with the arithmetical operations, and hence is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
. As it keeps the real numbers fixed, it is an element of the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of the field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
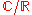 . This Galois group has only two elements:
. This Galois group has only two elements:  and the identity on
and the identity on  . Thus the only two field automorphisms of
. Thus the only two field automorphisms of  that leave the real numbers fixed are the identity map and complex conjugation.
that leave the real numbers fixed are the identity map and complex conjugation.Use as a variable
Once a complex number or
or 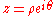 is given, its conjugate is sufficient to reproduce the parts of the z-variable:
is given, its conjugate is sufficient to reproduce the parts of the z-variable:
Thus the pair of variables
 and
and 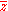 also serve up the plane as do x,y and
also serve up the plane as do x,y and 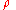 and
and  . Furthermore, the
. Furthermore, the 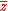 variable is useful in specifying lines in the plane:
variable is useful in specifying lines in the plane:
is a line through the origin and perpendicular to
 since the real part of
since the real part of 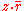 is zero only when the cosine of the angle between
is zero only when the cosine of the angle between  and
and  is zero. Similarly, for a fixed complex unit u = exp(b i), the equation:
is zero. Similarly, for a fixed complex unit u = exp(b i), the equation:
determines the line through
 in the direction of u.
in the direction of u.These uses of the conjugate of z as a variable are illustrated in Frank Morley
Frank Morley
Frank Morley was a leading mathematician, known mostly for his teaching and research in the fields of algebra and geometry...
's book Inversive Geometry (1933), written with his son Frank Vigor Morley.
Generalizations
The other planar real algebras, dual numbers, and split-complex numberSplit-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s are also explicated by use of complex conjugation.
For matrices of complex numbers
 .
.Taking the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
(or adjoint) of complex matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
generalizes complex conjugation. Even more general is the concept of adjoint operator for operators on (possibly infinite-dimensional) complex Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s. All this is subsumed by the *-operations of C*-algebras.
One may also define a conjugation for quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s and coquaternion
Coquaternion
In abstract algebra, the split-quaternions or coquaternions are elements of a 4-dimensional associative algebra introduced by James Cockle in 1849 under the latter name. Like the quaternions introduced by Hamilton in 1843, they form a four dimensional real vector space equipped with a...
s: the conjugate of
 is
is 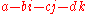 .
.Note that all these generalizations are multiplicative only if the factors are reversed:
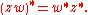
Since the multiplication of planar real algebras is commutative, this reversal is not needed there.
There is also an abstract notion of conjugation for vector spaces
 over the complex number
over the complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. In this context,
any antilinear map
 that satisfies
that satisfies-
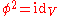 , where
, where  and
and  is the identity mapIdentity mapAn identity map is a database access design pattern used to improve performance by providing a context-specific in-memory cache to prevent duplicate retrieval of the same object data from the database....
is the identity mapIdentity mapAn identity map is a database access design pattern used to improve performance by providing a context-specific in-memory cache to prevent duplicate retrieval of the same object data from the database....
on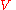 ,
, -
 for all
for all  ,
, 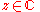 , and
, and -
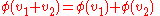 for all
for all  ,
, 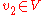 ,
,
is called a complex conjugation, or a real structure
Real structure
In mathematics, a real structure on a complex vector space is a way to decompose the complex vector space in the direct sum of two real vector spaces...
. As the involution
 is antilinear, it cannot be the identity map on
is antilinear, it cannot be the identity map on  .
.Of course,
 is a
is a  -linear transformation of
-linear transformation of  , if one notes that every complex space V has a real form obtained by taking the same vector
, if one notes that every complex space V has a real form obtained by taking the same vectorVector
Vector, a Latin word meaning "carrier", may refer in English to:-In computer science:*A one-dimensional array**Vector , a data type in the C++ Standard Template Library...
s as in the original set
Set
A set is a collection of well defined and distinct objects, considered as an object in its own right. Sets are one of the most fundamental concepts in mathematics. Developed at the end of the 19th century, set theory is now a ubiquitous part of mathematics, and can be used as a foundation from...
and restricting the scalars to be real. The above properties actually define a real structure
Real structure
In mathematics, a real structure on a complex vector space is a way to decompose the complex vector space in the direct sum of two real vector spaces...
on the complex vector space
 .
.One example of this notion is the conjugate transpose operation of complex matrices defined above. It should be remarked that on generic complex vector spaces there is no canonical
Canonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
notion of complex conjugation.