Axiom of choice
Encyclopedia
In mathematics
, the axiom of choice, or AC, is an axiom
of set theory
stating that for every family
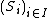of nonempty sets there exists a family 
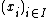of elements with 
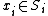for every 
. Informally put, the axiom of choice says that given any collection of bins, each containing at least one object, it is possible to make a selection of exactly one object from each bin. In many cases such a selection can be made without invoking the axiom of choice; this is in particular the case if the number of bins is finite, or if a selection rule is available: a distinguishing property that happens to hold for exactly one object in each bin. For example for any (even infinite) collection of pairs of shoes, one can pick out the left shoe from each pair to obtain an appropriate selection, but for an infinite collection of pairs of socks (assumed to have no distinguishing features), such a selection can be obtained only by invoking the axiom of choice.
The axiom of choice was formulated in 1904 by Ernst Zermelo
. Although originally controversial, it is now used without reservation by most mathematicians. One motivation for this use is that a number of important mathematical results, such as Tychonoff's theorem
, require the axiom of choice for their proofs. Contemporary set theorists also study axioms that are not compatible with the axiom of choice, such as the axiom of determinacy
. Unlike the axiom of choice, these alternatives are not ordinarily proposed as axioms for mathematics, but only as principles in set theory with interesting consequences.
Thus the negation of the axiom of choice states that there exists a set of nonempty sets which has no choice function.
Each choice function on a collection X of nonempty sets is an element of the Cartesian product
of the sets in X. This is not the most general situation of a Cartesian product of a family
of sets, where a same set can occur more than once as a factor; however, one can focus on elements of such a product that select the same element every time a given set appears as factor, and such elements correspond to an element of the Cartesian product of all distinct sets in the family. The axiom of choice asserts the existence of such elements; it is therefore equivalent to:
One variation avoids the use of choice functions by, in effect, replacing each choice function with its range.
Another equivalent axiom only considers collections X that are essentially powersets of other sets:
Authors who use this formulation often speak of the choice function on A, but be advised that this is a slightly different notion of choice function. Its domain is the powerset of A (with the empty set removed), and so makes sense for any set A, whereas with the definition used elsewhere in this article, the domain of a choice function on a collection of sets is that collection, and so only makes sense for sets of sets. With this alternate notion of choice function, the axiom of choice can be compactly stated as
which is equivalent to
The negation of the axiom can thus be expressed as:
without the axiom of choice (ZF); it is easily proved by mathematical induction
. In the even simpler case of a collection of one set, a choice function just corresponds to an element, so this instance of the axiom of choice says that every nonempty set has an element; this holds trivially. The axiom of choice can be seen as asserting the generalization of this property, already evident for finite collections, to arbitrary collections.
Not every situation requires the axiom of choice. For finite sets X, the axiom of choice follows from the other axioms of set theory. In that case it is equivalent to saying that if we have several (a finite number of) boxes, each containing at least one item, then we can choose exactly one item from each box. Clearly we can do this: We start at the first box, choose an item; go to the second box, choose an item; and so on. The number of boxes is finite, so eventually our choice procedure comes to an end. The result is an explicit choice function: a function that takes the first box to the first element we chose, the second box to the second element we chose, and so on. (A formal proof for all finite sets would use the principle of mathematical induction
to prove "for every natural number k, every family of k nonempty sets has a choice function.") This method cannot, however, be used to show that every countable family of nonempty sets has a choice function, as is asserted by the axiom of countable choice
. If the method is applied to an infinite sequence (Xi : i∈ω) of nonempty sets, a function is obtained at each finite stage, but there is no stage at which a choice function for the entire family is constructed, and no "limiting" choice function can be constructed, in general, in ZF without the axiom of choice.
The difficulty appears when there is no natural choice of elements from each set. If we cannot make explicit choices, how do we know that our set exists? For example, suppose that X is the set of all non-empty subsets of the real number
s. First we might try to proceed as if X were finite. If we try to choose an element from each set, then, because X is infinite, our choice procedure will never come to an end, and consequently, we will never be able to produce a choice function for all of X. Next we might try specifying the least element from each set. But some subsets of the real numbers do not have least elements. For example, the open interval (0,1) does not have a least element: if x is in (0,1), then so is x/2, and x/2 is always strictly smaller than x. So this attempt also fails.
Additionally, consider for instance the unit circle S, and the action on S by a group G consisting of all rational rotations. Namely, these are rotations by angles which are rational multiples of π. Here G is countable while S is uncountable. Hence S breaks up into uncountably many orbits under G. Using the axiom of choice, we could pick a single point from each orbit, obtaining an uncountable subset X of S with the property that all of its translates by G are disjoint from X. In other words, the circle gets partitioned into a countable collection of disjoint sets, which are all pairwise congruent. Now it is easy to convince oneself that the set X could not possibly be measurable for a countably additive measure. Hence one couldn't expect to find an algorithm to find a point in each orbit, without using the axiom of choice. See non-measurable set#Example for more details.
The reason that we are able to choose least elements from subsets of the natural numbers is the fact that the natural numbers are well-order
ed: every nonempty subset of the natural numbers has a unique least element under the natural ordering. One might say, "Even though the usual ordering of the real numbers does not work, it may be possible to find a different ordering of the real numbers which is a well-ordering. Then our choice function can choose the least element of every set under our unusual ordering." The problem then becomes that of constructing a well-ordering, which turns out to require the axiom of choice for its existence; every set can be well-ordered if and only if the axiom of choice holds.
the object in the language of set theory. For example, while the axiom of choice implies that there is a well-ordering of the real numbers, there are models of set theory with the axiom of choice in which no well-ordering of the reals is definable. As another example, a subset of the real numbers that is not Lebesgue measurable
can be proven to exist using the axiom of choice, but it is consistent that no such set is definable.
The axiom of choice produces these intangibles (objects that are proven to exist by a nonconstructive proof, but cannot be explicitly constructed), which may conflict with some philosophical principles. Because there is no canonical
well-ordering of all sets, a construction that relies on a well-ordering may not produce a canonical result, even if a canonical result is desired (as is often the case in category theory
). In constructivism
, all existence proofs are required to be totally explicit. That is, one must be able to construct, in an explicit and canonical manner, anything that is proven to exist. This foundation rejects the full axiom of choice because it asserts the existence of an object without uniquely determining its structure. In fact the Diaconescu–Goodman–Myhill theorem shows how to derive the constructively unacceptable law of the excluded middle, or a restricted form of it, in constructive set theory
from the assumption of the axiom of choice.
Another argument against the axiom of choice is that it implies the existence of counterintuitive objects. One example of this is the Banach–Tarski paradox
which says that it is possible to decompose ("carve up") the 3-dimensional solid unit ball into finitely many pieces and, using only rotations and translations, reassemble the pieces into two solid balls each with the same volume as the original. The pieces in this decomposition, constructed using the axiom of choice, are non-measurable set
s.
The majority of mathematicians accept the axiom of choice as a valid principle for proving new results in mathematics. The debate is interesting enough, however, that it is considered of note when a theorem in ZFC (ZF plus AC) is logically equivalent
(with just the ZF axioms) to the axiom of choice, and mathematicians look for results that require the axiom of choice to be false, though this type of deduction is less common than the type which requires the axiom of choice to be true.
It is possible to prove many theorems using neither the axiom of choice nor its negation; this is common in constructive mathematics. Such statements will be true in any model
of Zermelo–Fraenkel set theory
(ZF), regardless of the truth or falsity of the axiom of choice in that particular model. The restriction to ZF renders any claim that relies on either the axiom of choice or its negation unprovable. For example, the Banach–Tarski paradox is neither provable nor disprovable from ZF alone: it is impossible to construct the required decomposition of the unit ball in ZF, but also impossible to prove there is no such decomposition. Similarly, all the statements listed below which require choice or some weaker version thereof for their proof are unprovable in ZF, but since each is provable in ZF plus the axiom of choice, there are models of ZF in which each statement is true. Statements such as the Banach–Tarski paradox can be rephrased as conditional statements, for example, "If AC holds, the decomposition in the Banach–Tarski paradox exists." Such conditional statements are provable in ZF when the original statements are provable from ZF and the axiom of choice.
showed that the negation of the axiom of choice is not a theorem of ZF by constructing an inner model
(the constructible universe
) which satisfies ZFC and thus showing that ZFC is consistent. Assuming ZF is consistent, Paul Cohen
employed the technique of forcing
, developed for this purpose, to show that the axiom of choice itself is not a theorem of ZF by constructing a much more complex model which satisfies ZF¬C (ZF with the negation of AC added as axiom) and thus showing that ZF¬C is consistent. Together these results establish that the axiom of choice is logically independent
of ZF. The assumption that ZF is consistent is harmless because adding another axiom to an already inconsistent system cannot make the situation worse. Because of independence, the decision whether to use of the axiom of choice (or its negation) in a proof cannot be made by appeal to other axioms of set theory. The decision must be made on other grounds.
One argument given in favor of using the axiom of choice is that it is convenient to use it because it allows one to prove some simplifying propositions that otherwise could not be proved. Many theorems which are provable using choice are of an elegant general character: every ideal in a ring is contained in a maximal ideal, every vector space has a basis, and every product of compact spaces is compact. Without the axiom of choice, these theorems may not hold for mathematical objects of large cardinality.
The proof of the independence result also shows that a wide class of mathematical statements, including all statements that can be phrased in the language of Peano arithmetic, are provable in ZF if and only if they are provable in ZFC. Statements in this class include the statement that P = NP, the Riemann hypothesis
, and many other unsolved mathematical problems. When one attempts to solve problems in this class, it makes no difference whether ZF or ZFC is employed if the only question is the existence of a proof. It is possible, however, that there is a shorter proof of a theorem from ZFC than from ZF.
The axiom of choice is not the only significant statement which is independent of ZF. For example, the generalized continuum hypothesis (GCH) is not only independent of ZF, but also independent of ZFC. However, ZF plus GCH implies AC, making GCH a strictly stronger claim than AC, even though they are both independent of ZF.
and the generalized continuum hypothesis both imply the axiom of choice, but are strictly stronger than it.
In class theories such as Von Neumann–Bernays–Gödel set theory
and Morse–Kelley set theory
, there is a possible axiom called the axiom of global choice
which is stronger than the axiom of choice for sets because it also applies to proper classes. And the axiom of global choice follows from the axiom of limitation of size
.
but neither AC nor ¬AC, are equivalent to the axiom of choice. The most important among them are Zorn's lemma
and the well-ordering theorem
. In fact, Zermelo initially introduced the axiom of choice in order to formalize his proof of the well-ordering theorem.
which invoke the axiom of choice for their proof. These results might be weaker than, equivalent to, or stronger than the axiom of choice, depending on the strength of the technical foundations. For example, if one defines categories in terms of sets, that is, as sets of objects and morphisms (usually called a small category), or even locally small categories, whose hom-objects are sets, then there is no category of all sets
, and so it is difficult for a category-theoretic formulation to apply to all sets. On the other hand, other foundational descriptions of category theory are considerably stronger, and an identical category-theoretic statement of choice may be stronger than the standard formulation, à la class theory, mentioned above.
Examples of category-theoretic statements which require choice include:
(DC). A still weaker example is the axiom of countable choice
(ACω or CC), which states that a choice function exists for any countable set of nonempty sets. These axioms are sufficient for many proofs in elementary mathematical analysis
, and are consistent with some principles, such as the Lebesgue measurability of all sets of reals, that are disprovable from the full axiom of choice.
Other choice axioms weaker than axiom of choice include the Boolean prime ideal theorem
and the axiom of uniformization
. The former is equivalent in ZF to the existence of an ultrafilter
containing each given filter, proved by Tarski in 1930.
It is also consistent with ZF + DC that every set of reals is Lebesgue measurable; however, this consistency result, due to Robert M. Solovay
, cannot be proved in ZFC itself, but requires a mild large cardinal assumption (the existence of an inaccessible cardinal
). The much stronger axiom of determinacy
, or AD, implies that every set of reals is Lebesgue measurable, has the property of Baire, and has the perfect set property
(all three of these results are refuted by AC itself). ZF + DC + AD is consistent provided that a sufficiently strong large cardinal axiom is consistent (the existence of infinitely many Woodin cardinal
s).
Note that any model of ZF¬C is also a model of ZF, so for each of the following statements, there exists a model of ZF in which that statement is true.
For proofs, see Thomas Jech
, The Axiom of Choice, American Elsevier Pub. Co., New York, 1973.
obviously false, and who can tell about Zorn's lemma
?" — Jerry Bona
"The Axiom of Choice is necessary to select a set from an infinite number of socks, but not an infinite number of shoes." — Bertrand Russell
"Tarski tried to publish his theorem [the equivalence between AC and 'every infinite set A has the same cardinality as AxA, see above] in Comptes Rendus, but Fréchet
and Lebesgue
refused to present it. Fréchet wrote that an implication between two well known [true] propositions is not a new result, and Lebesgue wrote that an implication between two false propositions is of no interest".
"The axiom gets its name not because mathematicians prefer it to other axioms." — A. K. Dewdney
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the axiom of choice, or AC, is an axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
of set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
stating that for every family
Family of sets
In set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
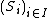of nonempty sets there exists a family 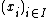of elements with 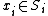for every . Informally put, the axiom of choice says that given any collection of bins, each containing at least one object, it is possible to make a selection of exactly one object from each bin. In many cases such a selection can be made without invoking the axiom of choice; this is in particular the case if the number of bins is finite, or if a selection rule is available: a distinguishing property that happens to hold for exactly one object in each bin. For example for any (even infinite) collection of pairs of shoes, one can pick out the left shoe from each pair to obtain an appropriate selection, but for an infinite collection of pairs of socks (assumed to have no distinguishing features), such a selection can be obtained only by invoking the axiom of choice.The axiom of choice was formulated in 1904 by Ernst Zermelo
Ernst Zermelo
Ernst Friedrich Ferdinand Zermelo was a German mathematician, whose work has major implications for the foundations of mathematics and hence on philosophy. He is known for his role in developing Zermelo–Fraenkel axiomatic set theory and his proof of the well-ordering theorem.-Life:He graduated...
. Although originally controversial, it is now used without reservation by most mathematicians. One motivation for this use is that a number of important mathematical results, such as Tychonoff's theorem
Tychonoff's theorem
In mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact. The theorem is named after Andrey Nikolayevich Tychonoff, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the...
, require the axiom of choice for their proofs. Contemporary set theorists also study axioms that are not compatible with the axiom of choice, such as the axiom of determinacy
Axiom of determinacy
The axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
. Unlike the axiom of choice, these alternatives are not ordinarily proposed as axioms for mathematics, but only as principles in set theory with interesting consequences.
Statement
A choice function is a function f, defined on a collection X of nonempty sets, such that for every set s in X, f(s) is an element of s. With this concept, the axiom can be stated:- For any set X of nonempty sets, there exists a choice function f defined on X.
Thus the negation of the axiom of choice states that there exists a set of nonempty sets which has no choice function.
Each choice function on a collection X of nonempty sets is an element of the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of the sets in X. This is not the most general situation of a Cartesian product of a family
Indexed family
In mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....
of sets, where a same set can occur more than once as a factor; however, one can focus on elements of such a product that select the same element every time a given set appears as factor, and such elements correspond to an element of the Cartesian product of all distinct sets in the family. The axiom of choice asserts the existence of such elements; it is therefore equivalent to:
- Given any family of nonempty sets, their Cartesian product is a nonempty set.
Nomenclature ZF, AC, and ZFC
In this article and other discussions of the Axiom of Choice the following abbreviations are common:- AC – the Axiom of Choice.
- ZF – Zermelo–Fraenkel set theoryZermelo–Fraenkel set theoryIn mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
omitting the Axiom of Choice. - ZFC – Zermelo–Fraenkel set theoryZermelo–Fraenkel set theoryIn mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
, extended to include the Axiom of Choice.
Variants
There are many other equivalent statements of the axiom of choice. These are equivalent in the sense that, in the presence of other basic axioms of set theory, they imply the axiom of choice and are implied by it.One variation avoids the use of choice functions by, in effect, replacing each choice function with its range.
- Given any set X of pairwise disjoint non-empty sets, there exists at least one set C that contains exactly one element in common with each of the sets in X.
Another equivalent axiom only considers collections X that are essentially powersets of other sets:
- For any set A, the power set of A (with the empty set removed) has a choice function.
Authors who use this formulation often speak of the choice function on A, but be advised that this is a slightly different notion of choice function. Its domain is the powerset of A (with the empty set removed), and so makes sense for any set A, whereas with the definition used elsewhere in this article, the domain of a choice function on a collection of sets is that collection, and so only makes sense for sets of sets. With this alternate notion of choice function, the axiom of choice can be compactly stated as
- Every set has a choice function.
which is equivalent to
- For any set A there is a function f such that for any non-empty subset B of A, f(B) lies in B.
The negation of the axiom can thus be expressed as:
- There is a set A such that for all functions f (on the set of non-empty subsets of A), there is a B such that f(B) does not lie in B.
Restriction to finite sets
The statement of the axiom of choice does not specify whether the collection of nonempty sets is finite or infinite, and thus implies that every finite collection of nonempty sets has a choice function. However, that particular case is a theorem of Zermelo–Fraenkel set theoryZermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
without the axiom of choice (ZF); it is easily proved by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. In the even simpler case of a collection of one set, a choice function just corresponds to an element, so this instance of the axiom of choice says that every nonempty set has an element; this holds trivially. The axiom of choice can be seen as asserting the generalization of this property, already evident for finite collections, to arbitrary collections.
Usage
Until the late 19th century, the axiom of choice was often used implicitly, although it had not yet been formally stated. For example, after having established that the set X contains only non-empty sets, a mathematician might have said "let F(s) be one of the members of s for all s in X." In general, it is impossible to prove that F exists without the axiom of choice, but this seems to have gone unnoticed until Zermelo.Not every situation requires the axiom of choice. For finite sets X, the axiom of choice follows from the other axioms of set theory. In that case it is equivalent to saying that if we have several (a finite number of) boxes, each containing at least one item, then we can choose exactly one item from each box. Clearly we can do this: We start at the first box, choose an item; go to the second box, choose an item; and so on. The number of boxes is finite, so eventually our choice procedure comes to an end. The result is an explicit choice function: a function that takes the first box to the first element we chose, the second box to the second element we chose, and so on. (A formal proof for all finite sets would use the principle of mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
to prove "for every natural number k, every family of k nonempty sets has a choice function.") This method cannot, however, be used to show that every countable family of nonempty sets has a choice function, as is asserted by the axiom of countable choice
Axiom of countable choice
The axiom of countable choice or axiom of denumerable choice, denoted ACω, is an axiom of set theory, similar to the axiom of choice. It states that any countable collection of non-empty sets must have a choice function...
. If the method is applied to an infinite sequence (Xi : i∈ω) of nonempty sets, a function is obtained at each finite stage, but there is no stage at which a choice function for the entire family is constructed, and no "limiting" choice function can be constructed, in general, in ZF without the axiom of choice.
Examples
The nature of the individual nonempty sets in the collection may make it possible to avoid the axiom of choice even for certain infinite collections. For example, suppose that each member of the collection X is a nonempty subset of the natural numbers. Every such subset has a smallest element, so to specify our choice function we can simply say that it maps each set to the least element of that set. This gives us a definite choice of an element from each set, and makes it unnecessary to apply the axiom of choice.The difficulty appears when there is no natural choice of elements from each set. If we cannot make explicit choices, how do we know that our set exists? For example, suppose that X is the set of all non-empty subsets of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. First we might try to proceed as if X were finite. If we try to choose an element from each set, then, because X is infinite, our choice procedure will never come to an end, and consequently, we will never be able to produce a choice function for all of X. Next we might try specifying the least element from each set. But some subsets of the real numbers do not have least elements. For example, the open interval (0,1) does not have a least element: if x is in (0,1), then so is x/2, and x/2 is always strictly smaller than x. So this attempt also fails.
Additionally, consider for instance the unit circle S, and the action on S by a group G consisting of all rational rotations. Namely, these are rotations by angles which are rational multiples of π. Here G is countable while S is uncountable. Hence S breaks up into uncountably many orbits under G. Using the axiom of choice, we could pick a single point from each orbit, obtaining an uncountable subset X of S with the property that all of its translates by G are disjoint from X. In other words, the circle gets partitioned into a countable collection of disjoint sets, which are all pairwise congruent. Now it is easy to convince oneself that the set X could not possibly be measurable for a countably additive measure. Hence one couldn't expect to find an algorithm to find a point in each orbit, without using the axiom of choice. See non-measurable set#Example for more details.
The reason that we are able to choose least elements from subsets of the natural numbers is the fact that the natural numbers are well-order
Well-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
ed: every nonempty subset of the natural numbers has a unique least element under the natural ordering. One might say, "Even though the usual ordering of the real numbers does not work, it may be possible to find a different ordering of the real numbers which is a well-ordering. Then our choice function can choose the least element of every set under our unusual ordering." The problem then becomes that of constructing a well-ordering, which turns out to require the axiom of choice for its existence; every set can be well-ordered if and only if the axiom of choice holds.
Nonconstructive aspects
A proof requiring the axiom of choice is nonconstructive: even though the proof establishes the existence of an object, it may be impossible to defineDefinable set
In mathematical logic, a definable set is an n-ary relation on the domain of a structure whose elements are precisely those elements satisfying some formula in the language of that structure...
the object in the language of set theory. For example, while the axiom of choice implies that there is a well-ordering of the real numbers, there are models of set theory with the axiom of choice in which no well-ordering of the reals is definable. As another example, a subset of the real numbers that is not Lebesgue measurable
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
can be proven to exist using the axiom of choice, but it is consistent that no such set is definable.
The axiom of choice produces these intangibles (objects that are proven to exist by a nonconstructive proof, but cannot be explicitly constructed), which may conflict with some philosophical principles. Because there is no canonical
Canonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
well-ordering of all sets, a construction that relies on a well-ordering may not produce a canonical result, even if a canonical result is desired (as is often the case in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
). In constructivism
Constructivism (mathematics)
In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
, all existence proofs are required to be totally explicit. That is, one must be able to construct, in an explicit and canonical manner, anything that is proven to exist. This foundation rejects the full axiom of choice because it asserts the existence of an object without uniquely determining its structure. In fact the Diaconescu–Goodman–Myhill theorem shows how to derive the constructively unacceptable law of the excluded middle, or a restricted form of it, in constructive set theory
Constructive set theory
Constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. That is, it uses the usual first-order language of classical set theory, and although of course the logic is constructive, there is no explicit use of constructive types...
from the assumption of the axiom of choice.
Another argument against the axiom of choice is that it implies the existence of counterintuitive objects. One example of this is the Banach–Tarski paradox
Banach–Tarski paradox
The Banach–Tarski paradox is a theorem in set theoretic geometry which states the following: Given a solid ball in 3-dimensional space, there exists a decomposition of the ball into a finite number of non-overlapping pieces , which can then be put back together in a different way to yield two...
which says that it is possible to decompose ("carve up") the 3-dimensional solid unit ball into finitely many pieces and, using only rotations and translations, reassemble the pieces into two solid balls each with the same volume as the original. The pieces in this decomposition, constructed using the axiom of choice, are non-measurable set
Non-measurable set
In mathematics, a non-measurable set is a set whose structure is so complicated that it cannot be assigned any meaningful measure. Such sets are constructed to shed light on the notions of length, area and volume in formal set theory....
s.
The majority of mathematicians accept the axiom of choice as a valid principle for proving new results in mathematics. The debate is interesting enough, however, that it is considered of note when a theorem in ZFC (ZF plus AC) is logically equivalent
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
(with just the ZF axioms) to the axiom of choice, and mathematicians look for results that require the axiom of choice to be false, though this type of deduction is less common than the type which requires the axiom of choice to be true.
It is possible to prove many theorems using neither the axiom of choice nor its negation; this is common in constructive mathematics. Such statements will be true in any model
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
(ZF), regardless of the truth or falsity of the axiom of choice in that particular model. The restriction to ZF renders any claim that relies on either the axiom of choice or its negation unprovable. For example, the Banach–Tarski paradox is neither provable nor disprovable from ZF alone: it is impossible to construct the required decomposition of the unit ball in ZF, but also impossible to prove there is no such decomposition. Similarly, all the statements listed below which require choice or some weaker version thereof for their proof are unprovable in ZF, but since each is provable in ZF plus the axiom of choice, there are models of ZF in which each statement is true. Statements such as the Banach–Tarski paradox can be rephrased as conditional statements, for example, "If AC holds, the decomposition in the Banach–Tarski paradox exists." Such conditional statements are provable in ZF when the original statements are provable from ZF and the axiom of choice.
Independence
Assuming ZF is consistent, Kurt GödelKurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
showed that the negation of the axiom of choice is not a theorem of ZF by constructing an inner model
Inner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
(the constructible universe
Constructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
) which satisfies ZFC and thus showing that ZFC is consistent. Assuming ZF is consistent, Paul Cohen
Paul Cohen (mathematician)
Paul Joseph Cohen was an American mathematician best known for his proof of the independence of the continuum hypothesis and the axiom of choice from Zermelo–Fraenkel set theory, the most widely accepted axiomatization of set theory.-Early years:Cohen was born in Long Branch, New Jersey, into a...
employed the technique of forcing
Forcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
, developed for this purpose, to show that the axiom of choice itself is not a theorem of ZF by constructing a much more complex model which satisfies ZF¬C (ZF with the negation of AC added as axiom) and thus showing that ZF¬C is consistent. Together these results establish that the axiom of choice is logically independent
Independence (mathematical logic)
In mathematical logic, independence refers to the unprovability of a sentence from other sentences.A sentence σ is independent of a given first-order theory T if T neither proves nor refutes σ; that is, it is impossible to prove σ from T, and it is also impossible to prove from T that...
of ZF. The assumption that ZF is consistent is harmless because adding another axiom to an already inconsistent system cannot make the situation worse. Because of independence, the decision whether to use of the axiom of choice (or its negation) in a proof cannot be made by appeal to other axioms of set theory. The decision must be made on other grounds.
One argument given in favor of using the axiom of choice is that it is convenient to use it because it allows one to prove some simplifying propositions that otherwise could not be proved. Many theorems which are provable using choice are of an elegant general character: every ideal in a ring is contained in a maximal ideal, every vector space has a basis, and every product of compact spaces is compact. Without the axiom of choice, these theorems may not hold for mathematical objects of large cardinality.
The proof of the independence result also shows that a wide class of mathematical statements, including all statements that can be phrased in the language of Peano arithmetic, are provable in ZF if and only if they are provable in ZFC. Statements in this class include the statement that P = NP, the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
, and many other unsolved mathematical problems. When one attempts to solve problems in this class, it makes no difference whether ZF or ZFC is employed if the only question is the existence of a proof. It is possible, however, that there is a shorter proof of a theorem from ZFC than from ZF.
The axiom of choice is not the only significant statement which is independent of ZF. For example, the generalized continuum hypothesis (GCH) is not only independent of ZF, but also independent of ZFC. However, ZF plus GCH implies AC, making GCH a strictly stronger claim than AC, even though they are both independent of ZF.
Stronger axioms
The axiom of constructibilityAxiom of constructibility
The axiom of constructibility is a possible axiom for set theory in mathematics that asserts that every set is constructible. The axiom is usually written as V = L, where V and L denote the von Neumann universe and the constructible universe, respectively.- Implications :The axiom of...
and the generalized continuum hypothesis both imply the axiom of choice, but are strictly stronger than it.
In class theories such as Von Neumann–Bernays–Gödel set theory
Von Neumann–Bernays–Gödel set theory
In the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
and Morse–Kelley set theory
Morse–Kelley set theory
In the foundation of mathematics, Morse–Kelley set theory or Kelley–Morse set theory is a first order axiomatic set theory that is closely related to von Neumann–Bernays–Gödel set theory...
, there is a possible axiom called the axiom of global choice
Axiom of global choice
In class theories, the axiom of global choice is a stronger variant of the axiom of choice which applies to proper classes as well as sets.- Statement :The axiom can be expressed in various ways which are equivalent:...
which is stronger than the axiom of choice for sets because it also applies to proper classes. And the axiom of global choice follows from the axiom of limitation of size
Axiom of limitation of size
In class theories, the axiom of limitation of size says that for any class C, C is a proper class, that is a class which is not a set , if and only if it can be mapped onto the class V of all sets....
.
Equivalents
There are important statements that, assuming the axioms of ZFZermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
but neither AC nor ¬AC, are equivalent to the axiom of choice. The most important among them are Zorn's lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
and the well-ordering theorem
Well-ordering theorem
In mathematics, the well-ordering theorem states that every set can be well-ordered. A set X is well-ordered by a strict total order if every non-empty subset of X has a least element under the ordering. This is also known as Zermelo's theorem and is equivalent to the Axiom of Choice...
. In fact, Zermelo initially introduced the axiom of choice in order to formalize his proof of the well-ordering theorem.
- Set theorySet theorySet theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
- Well-ordering theoremWell-ordering theoremIn mathematics, the well-ordering theorem states that every set can be well-ordered. A set X is well-ordered by a strict total order if every non-empty subset of X has a least element under the ordering. This is also known as Zermelo's theorem and is equivalent to the Axiom of Choice...
: Every set can be well-ordered. Consequently, every cardinalCardinal numberIn mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
has an initial ordinal. - TarskiAlfred TarskiAlfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
's theorem: For every infinite set A, there is a bijective map between the sets A and A×A. - Trichotomy: If two sets are given, then either they have the same cardinality, or one has a smaller cardinality than the other.
- The Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of any family of nonempty sets is nonempty. - König's theoremKönig's theorem (set theory)In set theory, König's theorem colloquially states that if the axiom of choice holds, I is a set, mi and ni are cardinal numbers for every i in I, and m_i In set theory, König's theorem In set theory, König's theorem (named after the Hungarian mathematician Gyula Kőnig, who published under the...
: Colloquially, the sum of a sequence of cardinals is strictly less than the product of a sequence of larger cardinals. (The reason for the term "colloquially", is that the sum or product of a "sequence" of cardinals cannot be defined without some aspect of the axiom of choice.) - Every surjective functionSurjective functionIn mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
has a right inverse.
- Well-ordering theorem
- Order theoryOrder theoryOrder theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
- Zorn's lemmaZorn's lemmaZorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
: Every non-empty partially ordered set in which every chain (i.e. totally ordered subset) has an upper bound contains at least one maximal element. - Hausdorff maximal principleHausdorff maximal principleIn mathematics, the Hausdorff maximal principle is an alternate and earlier formulation of Zorn's lemma proved by Felix Hausdorff in 1914...
: In any partially ordered set, every totally ordered subset is contained in a maximal totally ordered subset. The restricted principle "Every partially ordered set has a maximal totally ordered subset" is also equivalent to AC over ZF. - Tukey's lemmaTukey's lemmaIn mathematics, Tukey's lemma, named after John Tukey, states that every nonempty collection of finite character has a maximal element with respect to inclusion. It is equivalent to the Axiom of Choice.- References :* Brillinger, David R. "John Wilder Tukey"...
: Every non-empty collection of finite character has a maximal element with respect to inclusion. - AntichainAntichainIn mathematics, in the area of order theory, an antichain is a subset of a partially ordered set such that any two elements in the subset are incomparable. Let S be a partially ordered set...
principle: Every partially ordered set has a maximal antichainAntichainIn mathematics, in the area of order theory, an antichain is a subset of a partially ordered set such that any two elements in the subset are incomparable. Let S be a partially ordered set...
.
- Zorn's lemma
- Abstract algebraAbstract algebraAbstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
- Every vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
has a basisBasis (linear algebra)In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
. - Every unital ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
other than the trivial ring contains a maximal idealMaximal idealIn mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
. - For every non-empty set S there is a binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
defined on S that makes it a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. (A cancellativeCancellation propertyIn mathematics, the notion of cancellative is a generalization of the notion of invertible.An element a in a magma has the left cancellation property if for all b and c in M, a * b = a * c always implies b = c.An element a in a magma has the right cancellation...
binary operation is enough.)
- Every vector space
- Functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
- The closed unit ball of the dual of a normed vector spaceNormed vector spaceIn mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
over the reals has an extreme pointExtreme pointIn mathematics, an extreme point of a convex set S in a real vector space is a point in S which does not lie in any open line segment joining two points of S...
.
- The closed unit ball of the dual of a normed vector space
- General topologyGeneral topologyIn mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
- Tychonoff's theoremTychonoff's theoremIn mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact. The theorem is named after Andrey Nikolayevich Tychonoff, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the...
stating that every productProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s is compact. - In the product topology, the closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of a product of subsets is equal to the product of the closures.
- Tychonoff's theorem
- Mathematical logicMathematical logicMathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
- If S is a set of sentences of first-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
and B is a consistent subset of S, then B is included in a set that is maximal among consistent subsets of S. The special case where S is the set of all first-order sentences in a given signatureSignature (logic)In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
is weaker, equivalent to the Boolean prime ideal theoremBoolean prime ideal theoremIn mathematics, a prime ideal theorem guarantees the existence of certain types of subsets in a given abstract algebra. A common example is the Boolean prime ideal theorem, which states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on...
; see the section "Weaker forms" below.
- If S is a set of sentences of first-order logic
Category theory
There are several results in category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
which invoke the axiom of choice for their proof. These results might be weaker than, equivalent to, or stronger than the axiom of choice, depending on the strength of the technical foundations. For example, if one defines categories in terms of sets, that is, as sets of objects and morphisms (usually called a small category), or even locally small categories, whose hom-objects are sets, then there is no category of all sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, and so it is difficult for a category-theoretic formulation to apply to all sets. On the other hand, other foundational descriptions of category theory are considerably stronger, and an identical category-theoretic statement of choice may be stronger than the standard formulation, à la class theory, mentioned above.
Examples of category-theoretic statements which require choice include:
- Every small categoryCategory (mathematics)In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
has a skeletonSkeleton (category theory)In mathematics, a skeleton of a category is a subcategory which, roughly speaking, does not contain any extraneous isomorphisms. In a certain sense, the skeleton of a category is the "smallest" equivalent category which captures all "categorical properties". In fact, two categories are equivalent...
. - If two small categories are weakly equivalent, then they are equivalentEquivalence of categoriesIn category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
. - Every continuous functor on a small-complete category which satisfies the appropriate solution set condition has a left-adjointAdjoint functorsIn mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
(the Freyd adjoint functor theorem).
Weaker forms
There are several weaker statements that are not equivalent to the axiom of choice, but are closely related. One example is the axiom of dependent choiceAxiom of dependent choice
In mathematics, the axiom of dependent choices, denoted DC, is a weak form of the axiom of choice which is still sufficient to develop most of real analysis...
(DC). A still weaker example is the axiom of countable choice
Axiom of countable choice
The axiom of countable choice or axiom of denumerable choice, denoted ACω, is an axiom of set theory, similar to the axiom of choice. It states that any countable collection of non-empty sets must have a choice function...
(ACω or CC), which states that a choice function exists for any countable set of nonempty sets. These axioms are sufficient for many proofs in elementary mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, and are consistent with some principles, such as the Lebesgue measurability of all sets of reals, that are disprovable from the full axiom of choice.
Other choice axioms weaker than axiom of choice include the Boolean prime ideal theorem
Boolean prime ideal theorem
In mathematics, a prime ideal theorem guarantees the existence of certain types of subsets in a given abstract algebra. A common example is the Boolean prime ideal theorem, which states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on...
and the axiom of uniformization
Uniformization (set theory)
In set theory, the axiom of uniformization, a weak form of the axiom of choice, states that if R is a subset of X\times Y, where X and Y are Polish spaces,...
. The former is equivalent in ZF to the existence of an ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
containing each given filter, proved by Tarski in 1930.
Results requiring AC (or weaker forms) but weaker than it
One of the most interesting aspects of the axiom of choice is the large number of places in mathematics that it shows up. Here are some statements that require the axiom of choice in the sense that they are not provable from ZF but are provable from ZFC (ZF plus AC). Equivalently, these statements are true in all models of ZFC but false in some models of ZF.- Set theorySet theorySet theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
- Any unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of countably many countable sets is itself countable. - If the set A is infinite, then there exists an injectionInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
from the natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s N to A (see Dedekind infinite). - Every infinite game
in which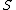 
is a BorelBorel setIn mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
subset of Baire spaceBaire space (set theory)In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is often denoted B, N'N, or ωω...
is determined.
- Any union
- Measure theory
- The Vitali theoremVitali setIn mathematics, a Vitali set is an elementary example of a set of real numbers that is not Lebesgue measurable, found by . The Vitali theorem is the existence theorem that there are such sets. There are uncountably many Vitali sets, and their existence is proven on the assumption of the axiom of...
on the existence of non-measurable setNon-measurable setIn mathematics, a non-measurable set is a set whose structure is so complicated that it cannot be assigned any meaningful measure. Such sets are constructed to shed light on the notions of length, area and volume in formal set theory....
s which states that there is a subset of the real numbers that is not Lebesgue measurable. - The Hausdorff paradoxHausdorff paradoxIn mathematics, the Hausdorff paradox, named after Felix Hausdorff, states that if you remove a certain countable subset of the sphere S2, the remainder can be divided into three disjoint subsets A, B and C such that A, B, C and B ∪ C are all congruent...
. - The Banach–Tarski paradoxBanach–Tarski paradoxThe Banach–Tarski paradox is a theorem in set theoretic geometry which states the following: Given a solid ball in 3-dimensional space, there exists a decomposition of the ball into a finite number of non-overlapping pieces , which can then be put back together in a different way to yield two...
. - The Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
of a countable disjoint unionDisjoint unionIn mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of measurable sets is equal to the sum of the measures of the individual sets.
- The Vitali theorem
- AlgebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
- Every fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
has an algebraic closureAlgebraic closureIn mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
. - Every field extensionField extensionIn abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
has a transcendence basis. - Stone's representation theorem for Boolean algebrasStone's representation theorem for Boolean algebrasIn mathematics, Stone's representation theorem for Boolean algebras states that every Boolean algebra is isomorphic to a field of sets. The theorem is fundamental to the deeper understanding of Boolean algebra that emerged in the first half of the 20th century. The theorem was first proved by Stone...
needs the Boolean prime ideal theoremBoolean prime ideal theoremIn mathematics, a prime ideal theorem guarantees the existence of certain types of subsets in a given abstract algebra. A common example is the Boolean prime ideal theorem, which states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on...
. - The Nielsen–Schreier theoremNielsen–Schreier theoremIn group theory, a branch of mathematics, the Nielsen–Schreier theorem is the statement that every subgroup of a free group is itself free. It is named after Jakob Nielsen and Otto Schreier.-Statement of the theorem:...
, that every subgroup of a free group is free. - The additive groups of R and C are isomorphic. and
- Every field
- Functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
- The Hahn–Banach theoremHahn–Banach theoremIn mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
in functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, allowing the extension of linear functionals - The theorem that every Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
has an orthonormal basis. - The Banach–Alaoglu theorem about compactness of sets of functionals.
- The Baire category theoremBaire category theoremThe Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
about completeComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s, and its consequences, such as the open mapping theoremOpen mapping theorem (functional analysis)In functional analysis, the open mapping theorem, also known as the Banach–Schauder theorem , is a fundamental result which states that if a continuous linear operator between Banach spaces is surjective then it is an open map...
and the closed graph theoremClosed graph theoremIn mathematics, the closed graph theorem is a basic result in functional analysis which characterizes continuous linear operators between Banach spaces in terms of the operator graph.- The closed graph theorem :...
. - On every infinite-dimensional topological vector space there is a discontinuous linear mapDiscontinuous linear mapIn mathematics, linear maps form an important class of "simple" functions which preserve the algebraic structure of linear spaces and are often used as approximations to more general functions . If the spaces involved are also topological spaces , then it makes sense to ask whether all linear maps...
.
- The Hahn–Banach theorem
- General topologyGeneral topologyIn mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
- A uniform space is compact if and only if it is complete and totally bounded.
- Every Tychonoff spaceTychonoff spaceIn topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
has a Stone–Čech compactificationStone–Cech compactificationIn the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
.
- Mathematical logicMathematical logicMathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
- Gödel's completeness theoremGödel's completeness theoremGödel's completeness theorem is a fundamental theorem in mathematical logic that establishes a correspondence between semantic truth and syntactic provability in first-order logic. It was first proved by Kurt Gödel in 1929....
for first-order logic: every consistent set of first-order sentences has a completion. That is, every consistent set of first-order sentences can be extended to a maximal consistent set.
- Gödel's completeness theorem
Stronger forms of the negation of AC
Now, consider stronger forms of the negation of AC. For example, if we abbreviate by BP the claim that every set of real numbers has the property of Baire, then BP is stronger than ¬AC, which asserts the nonexistence of any choice function on perhaps only a single set of nonempty sets. Note that strengthened negations may be compatible with weakened forms of AC. For example, ZF + DC + BP is consistent, if ZF is.It is also consistent with ZF + DC that every set of reals is Lebesgue measurable; however, this consistency result, due to Robert M. Solovay
Robert M. Solovay
Robert Martin Solovay is an American mathematician specializing in set theory.Solovay earned his Ph.D. from the University of Chicago in 1964 under the direction of Saunders Mac Lane, with a dissertation on A Functorial Form of the Differentiable Riemann–Roch theorem...
, cannot be proved in ZFC itself, but requires a mild large cardinal assumption (the existence of an inaccessible cardinal
Inaccessible cardinal
In set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...
). The much stronger axiom of determinacy
Axiom of determinacy
The axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
, or AD, implies that every set of reals is Lebesgue measurable, has the property of Baire, and has the perfect set property
Perfect set property
In descriptive set theory, a subset of a Polish space has the perfect set property if it is either countable or has a nonempty perfect subset...
(all three of these results are refuted by AC itself). ZF + DC + AD is consistent provided that a sufficiently strong large cardinal axiom is consistent (the existence of infinitely many Woodin cardinal
Woodin cardinal
In set theory, a Woodin cardinal is a cardinal number λ such that for all functionsthere exists a cardinal κ In set theory, a Woodin cardinal is a cardinal number λ such that for all functions...
s).
Statements consistent with the negation of AC
There are models of Zermelo-Fraenkel set theory in which the axiom of choice is false. We will abbreviate "Zermelo-Fraenkel set theory plus the negation of the axiom of choice" by ZF¬C. For certain models of ZF¬C, it is possible to prove the negation of some standard facts.Note that any model of ZF¬C is also a model of ZF, so for each of the following statements, there exists a model of ZF in which that statement is true.
- There exists a model of ZF¬C in which there is a function f from the real numbers to the real numbers such that f is not continuous at a, but f is sequentially continuous at a, i.e., for any sequence {xn} converging to a, limn f(xn)=f(a).
- There exists a model of ZF¬C which has an infinite set of real numbers without a countably infinite subset.
- There exists a model of ZF¬C in which real numbers are a countable union of countable sets.
- There exists a model of ZF¬C in which there is a field with no algebraic closure.
- In all models of ZF¬C there is a vector space with no basis.
- There exists a model of ZF¬C in which there is a vector space with two bases of different cardinalities.
- There exists a model of ZF¬C in which there is a free complete boolean algebraComplete Boolean algebraIn mathematics, a complete Boolean algebra is a Boolean algebra in which every subset has a supremum . Complete Boolean algebras are used to construct Boolean-valued models of set theory in the theory of forcing...
on countably many generators.
For proofs, see Thomas Jech
Thomas Jech
Thomas J. Jech is a mathematician specializing in set theory who was at Penn State for more than 25 years. He was educated at Charles University and is now at the of the Academy of Sciences of the Czech Republic....
, The Axiom of Choice, American Elsevier Pub. Co., New York, 1973.
- There exists a model of ZF¬C in which every set in Rn is measurable. Thus it is possible to exclude counterintuitive results like the Banach–Tarski paradoxBanach–Tarski paradoxThe Banach–Tarski paradox is a theorem in set theoretic geometry which states the following: Given a solid ball in 3-dimensional space, there exists a decomposition of the ball into a finite number of non-overlapping pieces , which can then be put back together in a different way to yield two...
which are provable in ZFC. Furthermore, this is possible whilst assuming the Axiom of dependent choiceAxiom of dependent choiceIn mathematics, the axiom of dependent choices, denoted DC, is a weak form of the axiom of choice which is still sufficient to develop most of real analysis...
, which is weaker than AC but sufficient to develop most of real analysisReal analysisReal analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
. - In all models of ZF¬C, the generalized continuum hypothesis does not hold.
Quotes
"The Axiom of Choice is obviously true, the well-ordering principleWell-ordering theorem
In mathematics, the well-ordering theorem states that every set can be well-ordered. A set X is well-ordered by a strict total order if every non-empty subset of X has a least element under the ordering. This is also known as Zermelo's theorem and is equivalent to the Axiom of Choice...
obviously false, and who can tell about Zorn's lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
?" — Jerry Bona
- This is a joke: although the three are all mathematically equivalent, many mathematicians find the axiom of choice to be intuitive, the well-ordering principle to be counterintuitive, and Zorn's lemma to be too complex for any intuition.
"The Axiom of Choice is necessary to select a set from an infinite number of socks, but not an infinite number of shoes." — Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
- The observation here is that one can define a function to select from an infinite number of pairs of shoes by stating for example, to choose the left shoe. Without the axiom of choice, one cannot assert that such a function exists for pairs of socks, because left and right socks are (presumably) indistinguishable from each other.
"Tarski tried to publish his theorem [the equivalence between AC and 'every infinite set A has the same cardinality as AxA, see above] in Comptes Rendus, but Fréchet
Maurice René Fréchet
Maurice Fréchet was a French mathematician. He made major contributions to the topology of point sets and introduced the entire concept of metric spaces. He also made several important contributions to the field of statistics and probability, as well as calculus...
and Lebesgue
Henri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
refused to present it. Fréchet wrote that an implication between two well known [true] propositions is not a new result, and Lebesgue wrote that an implication between two false propositions is of no interest".
- Polish-American mathematician Jan MycielskiJan MycielskiJan Mycielski is a Polish-American mathematician, a professor emeritus of mathematics at the University of Colorado at Boulder....
relates this anecdote in a 2006 article in the Notices of the AMS.
"The axiom gets its name not because mathematicians prefer it to other axioms." — A. K. Dewdney
- This quote comes from the famous April Fools' DayApril Fools' DayApril Fools' Day is celebrated in different countries around the world on April 1 every year. Sometimes referred to as All Fools' Day, April 1 is not a national holiday, but is widely recognized and celebrated as a day when many people play all kinds of jokes and foolishness...
article in the computer recreations column of the Scientific AmericanScientific AmericanScientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
, April 1989.
External links
- Axiom of Choice and Its Equivalents at ProvenMath includes formal statement of the Axiom of Choice, Hausdorff's Maximal Principle, Zorn's Lemma and formal proofs of their equivalence down to the finest detail.
- Consequences of the Axiom of Choice, based on the book by Paul Howard and Jean Rubin.