Timeline of mathematics
Encyclopedia
A timeline
of pure
and applied mathematics
history
.
Timeline
A timeline is a way of displaying a list of events in chronological order, sometimes described as a project artifact . It is typically a graphic design showing a long bar labeled with dates alongside itself and events labeled on points where they would have happened.-Uses of timelines:Timelines...
of pure
Pure mathematics
Broadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
and applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
history
History of mathematics
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past....
.
Before 1000 BC
- ca. 70,000 BCMiddle PaleolithicThe Middle Paleolithic is the second subdivision of the Paleolithic or Old Stone Age as it is understood in Europe, Africa and Asia. The term Middle Stone Age is used as an equivalent or a synonym for the Middle Paleolithic in African archeology. The Middle Paleolithic and the Middle Stone Age...
— South Africa, ochre rocks adorned with scratched geometricGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
patterns. - ca. 35,000 BC to 20,000 BCUpper PaleolithicThe Upper Paleolithic is the third and last subdivision of the Paleolithic or Old Stone Age as it is understood in Europe, Africa and Asia. Very broadly it dates to between 40,000 and 10,000 years ago, roughly coinciding with the appearance of behavioral modernity and before the advent of...
— Africa and France, earliest known prehistoricPrehistoryPrehistory is the span of time before recorded history. Prehistory can refer to the period of human existence before the availability of those written records with which recorded history begins. More broadly, it refers to all the time preceding human existence and the invention of writing...
attempts to quantify time. - c. 20,000 BC — Nile Valley, Ishango BoneIshango boneThe Ishango bone is a bone tool, dated to the Upper Paleolithic era. It is a dark brown length of bone, the fibula of a baboon, with a sharp piece of quartz affixed to one end, perhaps for engraving...
: possibly the earliest reference to prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s and Egyptian multiplication. - c. 3400 BC — MesopotamiaMesopotamiaMesopotamia is a toponym for the area of the Tigris–Euphrates river system, largely corresponding to modern-day Iraq, northeastern Syria, southeastern Turkey and southwestern Iran.Widely considered to be the cradle of civilization, Bronze Age Mesopotamia included Sumer and the...
, the Sumerians invent the first numeral systemNumeral systemA numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
, and a system of weights and measuresAncient Mesopotamian units of measurementAncient Mesopotamian units of measurement originated in the loosely organized city-states of Early Dynastic Sumer. The units themselves grew out of the tradition of counting tokens used by the Neolithic cultural complex of the Near East. The counting tokens were used to keep accounts of personal...
. - c. 3100 BC — EgyptEgyptEgypt , officially the Arab Republic of Egypt, Arabic: , is a country mainly in North Africa, with the Sinai Peninsula forming a land bridge in Southwest Asia. Egypt is thus a transcontinental country, and a major power in Africa, the Mediterranean Basin, the Middle East and the Muslim world...
, earliest known decimal systemDecimalThe decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
allows indefinite counting by way of introducing new symbols. - c. 2800 BC — Indus Valley CivilizationIndus Valley CivilizationThe Indus Valley Civilization was a Bronze Age civilization that was located in the northwestern region of the Indian subcontinent, consisting of what is now mainly modern-day Pakistan and northwest India...
on the Indian subcontinentIndian subcontinentThe Indian subcontinent, also Indian Subcontinent, Indo-Pak Subcontinent or South Asian Subcontinent is a region of the Asian continent on the Indian tectonic plate from the Hindu Kush or Hindu Koh, Himalayas and including the Kuen Lun and Karakoram ranges, forming a land mass which extends...
, earliest use of decimal ratios in a uniform system of ancient weights and measures, the smallest unit of measurement used is 1.704 millimetres and the smallest unit of mass used is 28 grams. - 2700 BC — Egypt, precision surveyingSurveyingSee Also: Public Land Survey SystemSurveying or land surveying is the technique, profession, and science of accurately determining the terrestrial or three-dimensional position of points and the distances and angles between them...
. - 2400 BC — Egypt, precise astronomical calendarEgyptian calendarThe ancient civil Egyptian calendar had a year that was 360 days long and was divided into 12 months of 30 days each, plus five extra days at the end of the year. The months were divided into three weeks of ten days each...
, used even in the Middle AgesMiddle AgesThe Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
for its mathematical regularity. - c. 2000 BC — Mesopotamia, the Babylonians use a base-60 positional numeral system, and compute the first known approximate value of πPi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
at 3.125. - c. 2000 BC — Scotland, Carved Stone BallsCarved Stone BallsCarved Stone Balls are petrospheres, usually round and rarely oval. They have from 3 to 160 protruding knobs on the surface. Their size is fairly uniform, they date from the late Neolithic to possibly the Iron Age and are mainly found in Scotland...
exhibit a variety of symmetries including all of the symmetries of Platonic solidPlatonic solidIn geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s. - 1800 BC — Moscow Mathematical PapyrusMoscow Mathematical PapyrusThe Moscow Mathematical Papyrus is an ancient Egyptian mathematical papyrus, also called the Golenishchev Mathematical Papyrus, after its first owner, Egyptologist Vladimir Golenishchev. Golenishchev bought the papyrus in 1892 or 1893 in Thebes...
, findings volume of a frustumFrustumIn geometry, a frustum is the portion of a solid that lies between two parallel planes cutting it....
. - 1650 BC — Rhind Mathematical PapyrusRhind Mathematical PapyrusThe Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
, copy of a lost scroll from around 1850 BC, the scribe AhmesAhmesAhmes was an ancient Egyptian scribe who lived during the Second Intermediate Period and the beginning of the Eighteenth Dynasty . He wrote the Rhind Mathematical Papyrus, a work of Ancient Egyptian mathematics that dates to approximately 1650 BC; he is the earliest contributor to mathematics...
presents one of the first known approximate values of π at 3.16, the first attempt at squaring the circleSquaring the circleSquaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
, earliest known use of a sort of cotangent, and knowledge of solving first order linear equations. - 1300 BC — Berlin papyrusBerlin papyrusThe Berlin Papyrus 6619, commonly known as the Berlin Papyrus, is an ancient Egyptian papyrus document from the Middle Kingdom. This papyrus was found at the ancient burial ground of Saqqara in the early 19th century CE....
(19th dynasty) contains a quadratic equation and its solution.
1st millennium BC
- c. 1000 BC — Vulgar fractions used by the EgyptiansEgyptiansEgyptians are nation an ethnic group made up of Mediterranean North Africans, the indigenous people of Egypt.Egyptian identity is closely tied to geography. The population of Egypt is concentrated in the lower Nile Valley, the small strip of cultivable land stretching from the First Cataract to...
. However, only unit fractions are used (i.e., those with 1 as the numerator) and interpolationInterpolationIn the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
tables are used to approximate the values of the other fractions. - first half of 1st millennium BC — Vedic India — YajnavalkyaYajnavalkyaYajnavalkya of Mithila was a legendary sage of Vedic India, credited with the authorship of the Shatapatha Brahmana , besides Yogayajnavalkya Samhita and the Yājñavalkya Smṛti...
, in his Shatapatha BrahmanaShatapatha BrahmanaThe Shatapatha Brahmana is one of the prose texts describing the Vedic ritual, associated with the Shukla Yajurveda. It survives in two recensions, Madhyandina and Kanva , with the former having the eponymous 100 adhyayas,7624 kandikas in 14 books, and the latter 104 adhyayas,6806 kandikas in 17...
, describes the motions of the sun and the moon, and advances a 95-year cycle to synchronize the motions of the sun and the moon. - c. 8th century BC — the Yajur Veda, one of the four HinduHinduHindu refers to an identity associated with the philosophical, religious and cultural systems that are indigenous to the Indian subcontinent. As used in the Constitution of India, the word "Hindu" is also attributed to all persons professing any Indian religion...
Vedas, contains the earliest concept of infinityInfinityInfinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
, and states that “if you remove a part from infinity or add a part to infinity, still what remains is infinity.” - 800 BC — BaudhayanaBaudhayanaBaudhāyana, was an Indian mathematician, whowas most likely also a priest. He is noted as the author of the earliest Sulba Sūtra—appendices to the Vedas giving rules for the construction of altars—called the , which contained several important mathematical results. He is older than the other...
, author of the Baudhayana Sulba SutraSulba SutrasThe Shulba Sutras or Śulbasūtras are sutra texts belonging to the Śrauta ritual and containing geometry related to fire-altar construction.- Purpose and origins :...
, a Vedic SanskritVedic SanskritVedic Sanskrit is an old Indo-Aryan language. It is an archaic form of Sanskrit, an early descendant of Proto-Indo-Iranian. It is closely related to Avestan, the oldest preserved Iranian language...
geometric text, contains quadratic equations, and calculates the square root of two correctly to five decimal places. - early 6th century BC — Thales of MiletusThalesThales of Miletus was a pre-Socratic Greek philosopher from Miletus in Asia Minor, and one of the Seven Sages of Greece. Many, most notably Aristotle, regard him as the first philosopher in the Greek tradition...
has various theorems attributed to him. - c. 600 BC — the other Vedic “Sulba Sutras” (“rule of chords” in SanskritSanskritSanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
) use Pythagorean triples, contain of a number of geometrical proofs, and approximate πPi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
at 3.16. - second half of 1st millennium BC — The Lo Shu SquareLo Shu SquareLo Shu Square |Luo ]] Book/Scroll) or the Nine Halls Diagram , is the unique normal magic square of order three. Lo Shu is part of the legacy of the most ancient Chinese mathematical and divinatory traditions, and is an important emblem in Feng Shui , the art of geomancy concerned with the...
, the unique normal magic squareMagic squareIn recreational mathematics, a magic square of order n is an arrangement of n2 numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. A normal magic square contains the integers from 1 to n2...
of order three, was discovered in China. - 530 BC — PythagorasPythagorasPythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
studies propositional geometryGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and vibrating lyre strings; his group also discovers the irrationalityIrrational numberIn mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
of the square root of two. - c. 500 BC — IndianHistory of IndiaThe history of India begins with evidence of human activity of Homo sapiens as long as 75,000 years ago, or with earlier hominids including Homo erectus from about 500,000 years ago. The Indus Valley Civilization, which spread and flourished in the northwestern part of the Indian subcontinent from...
grammarian Pānini writes the Astadhyayi, which contains the use of metarules, transformationsTransformation (mathematics)In mathematics, a transformation could be any function mapping a set X on to another set or on to itself. However, often the set X has some additional algebraic or geometric structure and the term "transformation" refers to a function from X to itself that preserves this structure.Examples include...
and recursionRecursionRecursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
s, originally for the purpose of systematizing the grammar of Sanskrit. - 5th century BC — Hippocrates of ChiosHippocrates of ChiosHippocrates of Chios was an ancient Greek mathematician, , and astronomer, who lived c. 470 – c. 410 BCE.He was born on the isle of Chios, where he originally was a merchant. After some misadventures he went to Athens, possibly for litigation...
utilizes lunesLune (mathematics)In geometry, a lune is either of two figures, both shaped roughly like a crescent Moon. The word "lune" derives from luna, the Latin word for Moon.-Plane geometry:...
in an attempt to square the circleSquaring the circleSquaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
. - 5th century BC — ApastambaApastambaThe Dharmasutra of Āpastamba forms a part of the larger Kalpasūtra of Āpastamba. It contains thirty praśnas, which literally means ‘questions’ or books. The subjects of this Dharmasūtra are well organized and preserved in good condition...
, author of the Apastamba Sulba Sutra, another Vedic Sanskrit geometric text, makes an attempt at squaring the circle and also calculates the square root of 2 correct to five decimal places. - c. 400 BC — Jaina mathematicians in India write the “Surya Prajinapti”, a mathematical text which classifies all numbers into three sets: enumerable, innumerable and infinite. It also recognises five different types of infinity: infinite in one and two directions, infinite in area, infinite everywhere, and infinite perpetually.
- 4th century BC — IndianIndian mathematicsIndian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
texts use the Sanskrit word “Shunya” to refer to the concept of ‘void’ (zero0 (number)0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
). - 370 BC — EudoxusEudoxus of CnidusEudoxus of Cnidus was a Greek astronomer, mathematician, scholar and student of Plato. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus's poem on astronomy...
states the method of exhaustionMethod of exhaustionThe method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
for areaAreaArea is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
determination. - 350 BC — AristotleAristotleAristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
discusses logicLogicIn philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
al reasoning in OrganonOrganonThe Organon is the name given by Aristotle's followers, the Peripatetics, to the standard collection of his six works on logic:* Categories* On Interpretation* Prior Analytics* Posterior Analytics...
. - 300 BC — Jain mathematicians in India write the “Bhagabati Sutra”, which contains the earliest information on combinations.
- 300 BC — EuclidEuclidEuclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
in his ElementsEuclid's ElementsEuclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
studies geometry as an axiomatic systemAxiomatic systemIn mathematics, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A mathematical theory consists of an axiomatic system and all its derived theorems...
, proves the infinitude of prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s and presents the Euclidean algorithmEuclidean algorithmIn mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
; he states the law of reflection in Catoptrics, and he proves the fundamental theorem of arithmeticFundamental theorem of arithmeticIn number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
. - c. 300 BC — Brahmi numeralBrahmi numeralThe Brahmi numerals are an indigenous Indian numeral system attested from the 3rd century BCE . They are the direct graphic ancestors of the modern Indic and Hindu-Arabic numerals. However, they were conceptually distinct from these later systems, as they were not used as a positional system with a...
s (the first positional base 10 numeral systemNumeral systemA numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
) are conceived in India. - 300 BC — MesopotamiaMesopotamiaMesopotamia is a toponym for the area of the Tigris–Euphrates river system, largely corresponding to modern-day Iraq, northeastern Syria, southeastern Turkey and southwestern Iran.Widely considered to be the cradle of civilization, Bronze Age Mesopotamia included Sumer and the...
, the Babylonians invent the earliest calculator, the abacusAbacusThe abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
. - c. 300 BC — Indian mathematician PingalaPingalaPingala is the traditional name of the author of the ' , the earliest known Sanskrit treatise on prosody.Nothing is known about Piṅgala himself...
writes the “Chhandah-shastra”, which contains the first Indian use of zero as a digit (indicated by a dot) and also presents a description of a binary numeral systemBinary numeral systemThe binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
, along with the first use of Fibonacci numbers and Pascal's trianglePascal's triangleIn mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
. - 260 BC — ArchimedesArchimedesArchimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
proved that the value of π lies between 3 + 1/7 (approx. 3.1429) and 3 + 10/71 (approx. 3.1408), that the area of a circle was equal to π multiplied by the square of the radius of the circle and that the area enclosed by a parabola and a straight line is 4/3 multiplied by the area of a triangle with equal base and height. He also gave a very accurate estimate of the value of the square root of 3. - c. 250 BC — late OlmecOlmecThe Olmec were the first major Pre-Columbian civilization in Mexico. They lived in the tropical lowlands of south-central Mexico, in the modern-day states of Veracruz and Tabasco....
s had already begun to use a true zero (a shell glyph) several centuries before PtolemyPtolemyClaudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
in the New World. See 0 (number)0 (number)0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
. - 240 BC — EratosthenesEratosthenesEratosthenes of Cyrene was a Greek mathematician, poet, athlete, geographer, astronomer, and music theorist.He was the first person to use the word "geography" and invented the discipline of geography as we understand it...
uses his sieve algorithmSieve of EratosthenesIn mathematics, the sieve of Eratosthenes , one of a number of prime number sieves, is a simple, ancient algorithm for finding all prime numbers up to a specified integer....
to quickly isolate prime numbers. - 225 BC — Apollonius of PergaApollonius of PergaApollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
writes On Conic SectionsConic sectionIn mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
and names the ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, and hyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
. - 150 BC — JainJainismJainism is an Indian religion that prescribes a path of non-violence towards all living beings. Its philosophy and practice emphasize the necessity of self-effort to move the soul towards divine consciousness and liberation. Any soul that has conquered its own inner enemies and achieved the state...
mathematicians in India write the “Sthananga Sutra”, which contains work on the theory of numbers, arithmetical operations, geometry, operations with fractions, simple equations, cubic equations, quartic equations, and permutations and combinations. - 140 BC — HipparchusHipparchusHipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
develops the bases of trigonometryTrigonometryTrigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
. - 50 BC — Indian numeralsIndian numeralsMost of the positional base 10 numeral systems in the world have originated from India, where the concept of positional numeration was first developed...
, a descendant of the Brahmi numerals (the first positional notationPositional notationPositional notation or place-value notation is a method of representing or encoding numbers. Positional notation is distinguished from other notations for its use of the same symbol for the different orders of magnitude...
base-10 numeral systemNumeral systemA numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
), begins development in IndiaHistory of IndiaThe history of India begins with evidence of human activity of Homo sapiens as long as 75,000 years ago, or with earlier hominids including Homo erectus from about 500,000 years ago. The Indus Valley Civilization, which spread and flourished in the northwestern part of the Indian subcontinent from...
. - final centuries BC — Indian astronomer Lagadha writes the “Vedanga Jyotisha”, a Vedic text on astronomyAstronomyAstronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
that describes rules for tracking the motions of the sun and the moon, and uses geometry and trigonometry for astronomy.
1st millennium AD
- 1st century — Heron of Alexandria, the earliest fleeting reference to square roots of negative numbers.
- c. 3rd century — PtolemyPtolemyClaudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
of AlexandriaAlexandriaAlexandria is the second-largest city of Egypt, with a population of 4.1 million, extending about along the coast of the Mediterranean Sea in the north central part of the country; it is also the largest city lying directly on the Mediterranean coast. It is Egypt's largest seaport, serving...
wrote the AlmagestAlmagestThe Almagest is a 2nd-century mathematical and astronomical treatise on the apparent motions of the stars and planetary paths. Written in Greek by Claudius Ptolemy, a Roman era scholar of Egypt,... - 250 — DiophantusDiophantusDiophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
uses symbols for unknown numbers in terms of syncopated algebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, and writes ArithmeticaArithmeticaArithmetica is an ancient Greek text on mathematics written by the mathematician Diophantus in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate equations and indeterminate equations.Equations in the book are called Diophantine equations...
, one of the earliest treatises on algebra - 300 — the earliest known use of zero0 (number)0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
as a decimal digit is introduced by Indian mathematicians - c. 340 — Pappus of AlexandriaPappus of AlexandriaPappus of Alexandria was one of the last great Greek mathematicians of Antiquity, known for his Synagoge or Collection , and for Pappus's Theorem in projective geometry...
states his hexagon theoremPappus's hexagon theoremIn mathematics, Pappus's hexagon theorem states that given one set of collinear points A, B, C, and another set of collinear points a, b, c, then the intersection points X, Y, Z of line pairs Ab and aB, Ac and aC, Bc and bC are collinear...
and his centroid theoremPappus's centroid theoremIn mathematics, Pappus' centroid theorem is either of two related theorems dealing with the surface areas and volumes of surfaces and solids of revolution.... - c. 400 — the “Bakhshali manuscript” is written by Jaina mathematicians, which describes a theory of the infinite containing different levels of infinityInfinityInfinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
, shows an understanding of indicesIndex (mathematics)The word index is used in variety of senses in mathematics.- General :* In perhaps the most frequent sense, an index is a number or other symbol that indicates the location of a variable in a list or array of numbers or other mathematical objects. This type of index is usually written as a...
, as well as logarithms to base 2, and computes square roots of numbers as large as a million correct to at least 11 decimal places - 450 — Zu ChongzhiZu ChongzhiZu Chongzhi , courtesy name Wenyuan , was a prominent Chinese mathematician and astronomer during the Liu Song and Southern Qi Dynasties.-Life and works:...
computes πPi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
to seven decimal places, - 500 — AryabhataAryabhataAryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
writes the “Aryabhata-Siddhanta”, which first introduces the trigonometric functions and methods of calculating their approximate numerical values. It defines the concepts of sineSineIn mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
and cosine, and also contains the earliest tables of sineĀryabhaṭa's sine tableĀryabhaṭa's sine table is a set of twenty-four of numbers given in the astronomical treatise Āryabhaṭiya composed by the fifth century Indian mathematician and astronomer Āryabhaṭa , for the computation of the half-chords of certain set of arcs of a circle...
and cosine values (in 3.75-degree intervals from 0 to 90 degrees) - 6th century — Aryabhata gives accurate calculations for astronomical constants, such as the solar eclipseSolar eclipseAs seen from the Earth, a solar eclipse occurs when the Moon passes between the Sun and the Earth, and the Moon fully or partially blocks the Sun as viewed from a location on Earth. This can happen only during a new moon, when the Sun and the Moon are in conjunction as seen from Earth. At least...
and lunar eclipseLunar eclipseA lunar eclipse occurs when the Moon passes behind the Earth so that the Earth blocks the Sun's rays from striking the Moon. This can occur only when the Sun, Earth, and Moon are aligned exactly, or very closely so, with the Earth in the middle. Hence, a lunar eclipse can only occur the night of a...
, computes π to four decimal places, and obtains whole number solutions to linear equations by a method equivalent to the modern method - 550 — HinduHinduHindu refers to an identity associated with the philosophical, religious and cultural systems that are indigenous to the Indian subcontinent. As used in the Constitution of India, the word "Hindu" is also attributed to all persons professing any Indian religion...
mathematicians give zero a numeral representation in the positional notationPositional notationPositional notation or place-value notation is a method of representing or encoding numbers. Positional notation is distinguished from other notations for its use of the same symbol for the different orders of magnitude...
Indian numeralIndian numeralsMost of the positional base 10 numeral systems in the world have originated from India, where the concept of positional numeration was first developed...
system - 7th century — Bhaskara IBhaskara IBhāskara was a 7th century Indian mathematician, who was apparently the first to write numbers in the Hindu-Arabic decimal system with a circle for the zero, and who gave a unique and remarkable rational approximation of the sine function in his commentary on Aryabhata's work...
gives a rational approximation of the sine function - 7th century — BrahmaguptaBrahmaguptaBrahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
invents the method of solving indeterminate equations of the second degree and is the first to use algebra to solve astronomical problems. He also develops methods for calculations of the motions and places of various planets, their rising and setting, conjunctions, and the calculation of eclipses of the sun and the moon - 628 — Brahmagupta writes the Brahma-sphuta-siddhantaBrahmasphutasiddhantaThe main work of Brahmagupta, Brāhmasphuṭasiddhānta , written c.628, contains ideas including a good understanding of the mathematical role of zero, rules for manipulating both negative and positive numbers, a method for computing square roots, methods of solving linear and some quadratic...
, where zero is clearly explained, and where the modern place-value Indian numeral system is fully developed. It also gives rules for manipulating both negative and positive numbers, methods for computing square roots, methods of solving linearLinear equationA linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
and quadratic equationQuadratic equationIn mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
s, and rules for summing seriesSeries (mathematics)A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
, Brahmagupta's identity, and the Brahmagupta theoremBrahmagupta theoremBrahmagupta's theorem is a result in geometry. It states that if a cyclic quadrilateral is orthodiagonal , then the perpendicular to a side from the point of intersection of the diagonals always bisects the opposite side... - 8th century — VirasenaVirasenaĀchārya Virasena was an 8th century Indian mathematician and Jain philosopher and scholar. He was a student of the Jain sage Elāchārya. He is also known to be a famous orator and an accomplished poet. His most reputed work is the Jain treatise Dhavala. Late Dr. Hiralal Jain places the completion of...
gives explicit rules for the Fibonacci sequence, gives the derivation of the volumeVolumeVolume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of a frustumFrustumIn geometry, a frustum is the portion of a solid that lies between two parallel planes cutting it....
using an infinite procedure, and also deals with the logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
to base 2 and knows its laws - 8th century — Shridhara gives the rule for finding the volume of a sphere and also the formula for solving quadratic equations
- 773 — Kanka brings Brahmagupta's Brahma-sphuta-siddhanta to BaghdadBaghdadBaghdad is the capital of Iraq, as well as the coterminous Baghdad Governorate. The population of Baghdad in 2011 is approximately 7,216,040...
to explain the Indian system of arithmetic astronomyAstronomyAstronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
and the Indian numeral system - 773 — Al Fazaii translates the Brahma-sphuta-siddhanta into Arabic upon the request of King Khalif Abbasid Al Mansoor
- 9th century — GovindsvaminGovindsvaminGovindasvamin was a 9th century Indian mathematician who gave the fractional parts of the Aryabhata's tabular sines.Govindaswamin who wrote commentary on mahabhaskariya of BHASKARA 1 belonged to Kerala in mahodayapuram. His work govindakriti was a sequel to Aryabhatiya and is lost...
discovers the Newton-Gauss interpolation formula, and gives the fractional parts of Aryabhata's tabular sines - 810 — The House of WisdomHouse of WisdomThe House of Wisdom was a library and translation institute established in Abbassid-era Baghdad, Iraq. It was a key institution in the Translation Movement and considered to have been a major intellectual centre during the Islamic Golden Age...
is built in Baghdad for the translation of Greek and SanskritSanskritSanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
mathematical works into Arabic. - 820 — Al-Khwarizmi — PersianPersian peopleThe Persian people are part of the Iranian peoples who speak the modern Persian language and closely akin Iranian dialects and languages. The origin of the ethnic Iranian/Persian peoples are traced to the Ancient Iranian peoples, who were part of the ancient Indo-Iranians and themselves part of...
mathematician, father of algebra, writes the Al-JabrThe Compendious Book on Calculation by Completion and Balancing, also known under a shorter name spelled as Hisab al-jabr w’al-muqabala, Kitab al-Jabr wa-l-Muqabala and other transliterations) is a mathematical book written in Arabic in approximately AD 820 by the Persian (Arabic for "The Compendious Book on Calculation by Completion and Balancing", in...
, later transliterated as AlgebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, which introduces systematic algebraic techniques for solving linear and quadratic equations. Translations of his book on arithmeticArithmeticArithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
will introduce the Hindu-ArabicArabic numeralsArabic numerals or Hindu numerals or Hindu-Arabic numerals or Indo-Arabic numerals are the ten digits . They are descended from the Hindu-Arabic numeral system developed by Indian mathematicians, in which a sequence of digits such as "975" is read as a numeral...
decimalDecimalThe decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
number system to the Western world in the 12th century. The term algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
is also named after him. - 820 — Al-MahaniAl-MahaniAbu-Abdullah Muhammad ibn Īsa Māhānī was a Persian mathematician and astronomer from Mahan, Kermān, Persia.A series of observations of lunar and solar eclipses and planetary conjunctions, made by him from 853 to 866, was in fact used by Ibn Yunus....
conceived the idea of reducing geometricalGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
problems such as doubling the cubeDoubling the cubeDoubling the cube is one of the three most famous geometric problems unsolvable by compass and straightedge construction...
to problems in algebra. - c. 850 — Al-KindiAl-Kindi' , known as "the Philosopher of the Arabs", was a Muslim Arab philosopher, mathematician, physician, and musician. Al-Kindi was the first of the Muslim peripatetic philosophers, and is unanimously hailed as the "father of Islamic or Arabic philosophy" for his synthesis, adaptation and promotion...
pioneers cryptanalysisCryptanalysisCryptanalysis is the study of methods for obtaining the meaning of encrypted information, without access to the secret information that is normally required to do so. Typically, this involves knowing how the system works and finding a secret key...
and frequency analysisFrequency analysisIn cryptanalysis, frequency analysis is the study of the frequency of letters or groups of letters in a ciphertext. The method is used as an aid to breaking classical ciphers....
in his book on cryptographyCryptographyCryptography is the practice and study of techniques for secure communication in the presence of third parties...
. - 895 — Thabit ibn QurraThabit ibn Qurra' was a mathematician, physician, astronomer and translator of the Islamic Golden Age.Ibn Qurra made important discoveries in algebra, geometry and astronomy...
: the only surviving fragment of his original work contains a chapter on the solution and properties of cubic equations. He also generalized the Pythagorean theoremPythagorean theoremIn mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, and discovered the theoremThabit numberIn number theory, a Thabit number, Thâbit ibn Kurrah number, or 321 number is an integer of the form 3·2n−1 for a non-negative integer n...
by which pairs of amicable numberAmicable numberAmicable numbers are two different numbers so related that the sum of the proper divisors of each is equal to the other number. A pair of amicable numbers constitutes an aliquot sequence of period 2...
s can be found, (i.e., two numbers such that each is the sum of the proper divisors of the other). - c. 900 — Abu KamilAbu Kamil' was an Egyptian Muslim mathematician during the Islamic Golden Age...
of Egypt had begun to understand what we would write in symbols as
- 940 — Abu'l-Wafa al-Buzjani extracts roots using the Indian numeral system.
- 953 — The arithmetic of the Hindu-Arabic numeral systemHindu-Arabic numeral systemThe Hindu–Arabic numeral system or Hindu numeral system is a positional decimal numeral system developed between the 1st and 5th centuries by Indian mathematicians, adopted by Persian and Arab mathematicians , and spread to the western world...
at first required the use of a dust board (a sort of handheld blackboardBlackboardA chalkboard is a reusable writing surface.Blackboard may also refer to:* Blackboards are synonymous with "boards of infamy", an element of agitation-propaganda in the Soviet Union in 1930s, coincidental with Holodomor...
) because “the methods required moving the numbers around in the calculation and rubbing some out as the calculation proceeded.” Al-Uqlidisi modified these methods for pen and paper use. Eventually the advances enabled by the decimal system led to its standard use throughout the region and the world. - 953 — Al-KarajiAl-Karaji' was a 10th century Persian Muslim mathematician and engineer. His three major works are Al-Badi' fi'l-hisab , Al-Fakhri fi'l-jabr wa'l-muqabala , and Al-Kafi fi'l-hisab .Because al-Karaji's original works in Arabic are lost, it is not...
is the “first person to completely free algebra from geometrical operations and to replace them with the arithmetical type of operations which are at the core of algebra today. He was first to define the monomialMonomialIn mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s
, 
, 
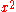, … and 
, 
, 
, … and 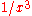to give rules for productsProduct (mathematics)In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of any two of these. He started a school of algebra which flourished for several hundreds of years”. He also discovered the binomial theoremBinomial theoremIn elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
for integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
exponents, which “was a major factor in the development of numerical analysisNumerical analysisNumerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
based on the decimal system.” - 975 — Al-Batani — Extended the Indian concepts of sine and cosine to other trigonometrical ratios, like tangent, secant and their inverse functions. Derived the formulae:
and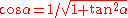 
.
1000–1500
- c. 1000 — Abū Sahl al-Qūhī (Kuhi) solves equationEquationAn equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
s higher than the second degreeQuadratic equationIn mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
. - c. 1000 — Abu-Mahmud al-Khujandi first states a special case of Fermat's Last TheoremFermat's Last TheoremIn number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
. - c. 1000 — Law of sinesLaw of sinesIn trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
is discovered by Muslim mathematiciansIslamic mathematicsIn the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
, but it is uncertain who discovers it first between Abu-Mahmud al-Khujandi, Abu Nasr MansurAbu Nasr MansurAbu Nasr Mansur ibn Ali ibn Iraq was a Persian Muslim mathematician. He is well known for his work with the spherical sine law....
, and Abu al-Wafa. - c. 1000 — Pope Sylvester II introduces the abacusAbacusThe abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
using the Hindu-Arabic numeral systemHindu-Arabic numeral systemThe Hindu–Arabic numeral system or Hindu numeral system is a positional decimal numeral system developed between the 1st and 5th centuries by Indian mathematicians, adopted by Persian and Arab mathematicians , and spread to the western world...
to Europe. - 1000 — Al-KarajiAl-Karaji' was a 10th century Persian Muslim mathematician and engineer. His three major works are Al-Badi' fi'l-hisab , Al-Fakhri fi'l-jabr wa'l-muqabala , and Al-Kafi fi'l-hisab .Because al-Karaji's original works in Arabic are lost, it is not...
writes a book containing the first known proofsMathematical proofIn mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
by mathematical inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. He used it to prove the binomial theoremBinomial theoremIn elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
, Pascal's trianglePascal's triangleIn mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
, and the sum of integralIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
cubes. He was “the first who introduced the theory of algebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
.” - c. 1000 — Ibn Tahir al-BaghdadiIbn Tahir al-BaghdadiAbu Mansur Abd al-Qahir ibn Tahir ibn Muhammad ibn Abdallah al-Tamimi al-Shaffi al-Baghdadi was an Arabian mathematician from Baghdad who is best known for his treatise al-Takmila fi'l-Hisab. It contains results in number theory, and comments on works by al-Khwarizmi which are now lost.-...
studied a slight variant of Thabit ibn QurraThabit ibn Qurra' was a mathematician, physician, astronomer and translator of the Islamic Golden Age.Ibn Qurra made important discoveries in algebra, geometry and astronomy...
's theorem on amicable numberAmicable numberAmicable numbers are two different numbers so related that the sum of the proper divisors of each is equal to the other number. A pair of amicable numbers constitutes an aliquot sequence of period 2...
s, and he also made improvements on the decimal system. - 1020 — Abul WáfaAbul WáfaAbū al-Wafāʾ, Muḥammad ibn Muḥammad ibn Yaḥyā ibn Ismāʿīl ibn al-ʿAbbās al-Būzjānī was a Persian mathematician and astronomer who worked in Baghdad...
— Gave this famous formula: sin (α + β) = sin α cos β + sin β cos α. Also discussed the quadrature of the parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
and the volume of the paraboloidParaboloidIn mathematics, a paraboloid is a quadric surface of special kind. There are two kinds of paraboloids: elliptic and hyperbolic. The elliptic paraboloid is shaped like an oval cup and can have a maximum or minimum point....
. - 1021 — Ibn al-Haytham formulated and solved “Alhazen's problem” geometrically.
- 1030 — Ali Ahmad NasawiAli Ahmad Nasawi' was a Persian mathematician from Khurasan, Iran. He flourished under the Buwayhid sultan Majd al-dowleh, who died in 1029-30AD, and under his successor. He wrote a book on arithmetic in Persian, and then Arabic, entitled the "Satisfying on Hindu Calculation"...
writes a treatise on the decimalDecimalThe decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
and sexagesimal number systems. His arithmetic explains the division of fractions and the extraction of square and cubic roots (square root of 57,342; cubic root of 3, 652, 296) in an almost modern manner. - 1070 — Omar KhayyámOmar KhayyámOmar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....
begins to write Treatise on Demonstration of Problems of Algebra and classifies cubic equations. - c. 1100 — Omar Khayyám “gave a complete classification of cubic equations with geometric solutions found by means of intersecting conic sectionConic sectionIn mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s.” He became the first to find general geometricGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
solutions of cubic equations and laid the foundations for the development of analytic geometryAnalytic geometryAnalytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
and non-Euclidean geometryNon-Euclidean geometryNon-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
. He also extracted roots using the decimal system (Hindu-Arabic numeral system). - 12th century — Indian numeralsIndian numeralsMost of the positional base 10 numeral systems in the world have originated from India, where the concept of positional numeration was first developed...
have been modified by Arab mathematicians to form the modern Hindu-Arabic numeral system (used universally in the modern world) - 12th century — the Hindu-Arabic numeral system reaches Europe through the Arabs
- 12th century — Bhaskara Acharya writes the LilavatiLilavatiLilavati was Indian mathematician Bhāskara II's treatise on mathematics. It is the first volume of his main work Siddhānta Shiromani, Sanskrit for "Crown of treatises," alongside Bijaganita, Grahaganita and Golādhyāya.- Name :The name comes from his daughter Līlāvatī...
, which covers the topics of definitions, arithmetical terms, interest computation, arithmetical and geometrical progressions, plane geometry, solid geometrySolid geometryIn mathematics, solid geometry was the traditional name for the geometry of three-dimensional Euclidean space — for practical purposes the kind of space we live in. It was developed following the development of plane geometry...
, the shadow of the gnomonGnomonThe gnomon is the part of a sundial that casts the shadow. Gnomon is an ancient Greek word meaning "indicator", "one who discerns," or "that which reveals."It has come to be used for a variety of purposes in mathematics and other fields....
, methods to solve indeterminate equations, and combinations - 12th century — Bhāskara II (Bhaskara Acharya) writes the “BijaganitaBijaganitaBijaganita was Indian mathematician Bhāskara II's treatise on algebra. It is the second volume of his main work Siddhānta Shiromani, Sanskrit for "Crown of treatises," alongside Lilāvati, Grahaganita and Golādhyāya.- Contents :...
” (“AlgebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
”), which is the first text to recognize that a positive number has two square roots - 12th century — Bhaskara Acharya conceives differential calculusDifferential calculusIn mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
, and also develops Rolle's theoremRolle's theoremIn calculus, Rolle's theorem essentially states that a differentiable function which attains equal values at two distinct points must have a point somewhere between them where the first derivative is zero.-Standard version of the theorem:If a real-valued function ƒ is continuous on a closed...
, Pell's equationPell's equationPell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
, a proof for the Pythagorean TheoremPythagorean theoremIn mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, proves that division by zero is infinity, computes πPi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
to 5 decimal places, and calculates the time taken for the earth to orbit the sun to 9 decimal places - 1130 — Al-SamawalAl-Samawal' commonly known as Samau'al al-Maghribi was a Muslim mathematician, astronomer and physician of Jewish descent. Though born to a Jewish family, he converted to Islam in 1163 after he had a dream telling him to do so...
gave a definition of algebra: “[it is concerned] with operating on unknowns using all the arithmetical tools, in the same way as the arithmetician operates on the known.” - 1135 — Sharafeddin TusiSharafeddin Tusi' was a Persian mathematician and astronomer of the Islamic Golden Age .- Biography :...
followed al-Khayyam's application of algebra to geometry, and wrote a treatise on cubic equations which “represents an essential contribution to another algebra which aimed to study curveCurveIn mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s by means of equations, thus inaugurating the beginning of algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.” - 1202 — Leonardo Fibonacci demonstrates the utility of Hindu-Arabic numerals in his Book of the Abacus.
- 1260 — Al-FarisiAl-FarisiKamal al-Din Hasan ibn Ali ibn Hasan Farisi or Abu Hasan Muhammad ibn Hasan ) was a prominent Persian born in Tabriz, Iran. He made two major contributions to science, one on optics, the other on number theory...
gave a new proof of Thabit ibn Qurra's theorem, introducing important new ideas concerning factorizationFactorizationIn mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
and combinatorialCombinatoricsCombinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
methods. He also gave the pair of amicable numbers 17296 and 18416 which have also been joint attributed to Fermat as well as Thabit ibn Qurra. - c. 1250 — Nasir Al-Din Al-TusiNasir al-Din al-TusiKhawaja Muḥammad ibn Muḥammad ibn Ḥasan Ṭūsī , better known as Naṣīr al-Dīn al-Ṭūsī , was a Persian polymath and prolific writer: an astronomer, biologist, chemist, mathematician, philosopher, physician, physicist, scientist, theologian and Marja Taqleed...
attempts to develop a form of non-Euclidean geometry. - 1303 — Zhu ShijieZhu ShijieZhu Shijie , courtesy name Hanqing , pseudonym Songting , was one of the greatest Chinese mathematicians lived during the Yuan Dynasty....
publishes Precious Mirror of the Four Elements, which contains an ancient method of arranging binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s in a triangle. - 14th century — MadhavaMadhava of SangamagramaMādhava of Sañgamāgrama was a prominent Kerala mathematician-astronomer from the town of Irińńālakkuţa near Cochin, Kerala, India. He is considered the founder of the Kerala School of Astronomy and Mathematics...
is considered the father of mathematical analysisMathematical analysisMathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, who also worked on the power series for p and for sine and cosine functions, and along with other Kerala schoolKerala schoolKerala school may refer to*Kerala school of astronomy and mathematics, a school of mathematics and astronomy founded by Madhava of Sangamagrama in Kerala, South India which flourished between the 14th and 16th centuries CE....
mathematicians, founded the important concepts of CalculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem... - 14th century — ParameshvaraParameshvaraVatasseri Parameshvara Nambudiri was a major Indian mathematician and astronomer of the Kerala school of astronomy and mathematics founded by Madhava of Sangamagrama. He was also an astrologer...
, a Kerala school mathematician, presents a series form of the sine function that is equivalent to its Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion, states the mean value theoremMean value theoremIn calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
of differential calculus, and is also the first mathematician to give the radius of circle with inscribed cyclic quadrilateralCyclic quadrilateralIn Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed... - 1400 — Madhava of Sangamagrama|Madhava discovers the series expansion for the inverse-tangent function, the infinite series for arctan and sin, and many methods for calculating the circumference of the circle, and uses them to compute π correct to 11 decimal places
- c. 1400 — Ghiyath al-Kashi “contributed to the development of decimal fractions not only for approximating algebraic numberAlgebraic numberIn mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s, but also for real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s such as π. His contribution to decimal fractions is so major that for many years he was considered as their inventor. Although not the first to do so, al-Kashi gave an algorithm for calculating nth rootNth rootIn mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
s which is a special case of the methods given many centuries later by RuffiniPaolo RuffiniPaolo Ruffini was an Italian mathematician and philosopher.By 1788 he had earned university degrees in philosophy, medicine/surgery, and mathematics...
and HornerWilliam George HornerWilliam George Horner was a British mathematician and schoolmaster. The invention of the zoetrope, in 1834 and under a different name , has been attributed to him.-Life:...
.” He is also the first to use the decimal point notation in arithmeticArithmeticArithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
and Arabic numeralsArabic numeralsArabic numerals or Hindu numerals or Hindu-Arabic numerals or Indo-Arabic numerals are the ten digits . They are descended from the Hindu-Arabic numeral system developed by Indian mathematicians, in which a sequence of digits such as "975" is read as a numeral...
. His works include The Key of arithmetics, Discoveries in mathematics, The Decimal point, and The benefits of the zero. The contents of the Benefits of the Zero are an introduction followed by five essays: “On whole number arithmetic”, “On fractional arithmetic”, “On astrology”, “On areas”, and “On finding the unknowns [unknown variables]”. He also wrote the Thesis on the sine and the chord and Thesis on finding the first degree sine. - 15th century — Ibn al-BannaIbn al-BannaIbn al‐Bannāʾ al‐Marrākushī al-Azdi also known as Abu'l-Abbas Ahmad ibn Muhammad ibn Uthman al-Azdi. [29) December 1256 – c. 1321) was a Moroccan mathematician, astronomer, Islamic scholar, Sufi, and a one time astrologer....
and al-Qalasadi introduced symbolic notationMathematical notationMathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
for algebra and for mathematics in general. - 15th century — Nilakantha SomayajiNilakantha SomayajiKelallur Nilakantha Somayaji was a major mathematician and astronomer of the Kerala school of astronomy and mathematics. One of his most influential works was the comprehensive astronomical treatise Tantrasamgraha completed in 1501...
, a Kerala school mathematician, writes the “Aryabhatiya Bhasya”, which contains work on infinite-series expansions, problems of algebra, and spherical geometry - 1424 — Ghiyath al-Kashi computes π to sixteen decimal places using inscribed and circumscribed polygons.
- 1427 — Al-Kashi completes The Key to Arithmetic containing work of great depth on decimal fractions. It applies arithmetical and algebraic methods to the solution of various problems, including several geometric ones.
- 1478 — An anonymous author writes the Treviso ArithmeticTreviso ArithmeticThe Treviso Arithmetic, or Arte dell'Abbaco, is an anonymous textbook in commercial arithmetic written in vernacular Venetian and published in Treviso, Italy in 1478.The author tells us the reason for writing this textbook:...
. - 1494 — Luca PacioliLuca PacioliFra Luca Bartolomeo de Pacioli was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and seminal contributor to the field now known as accounting...
writes "Summa de arithmetica, geometria, proportioni et proportionalità"; introduces primitive symbolic algebra using "co" (cosa) for the unknown.
16th century
- 1501 — Nilakantha SomayajiNilakantha SomayajiKelallur Nilakantha Somayaji was a major mathematician and astronomer of the Kerala school of astronomy and mathematics. One of his most influential works was the comprehensive astronomical treatise Tantrasamgraha completed in 1501...
writes the “Tantra Samgraha”, which lays the foundation for a complete system of fluxions (derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s), and expands on concepts from his previous text, the “Aryabhatiya Bhasya”. - 1520 — Scipione dal Ferro develops a method for solving “depressed” cubic equations (cubic equations without an x2 term), but does not publish.
- 1522 — Adam RiesAdam RiesAdam Ries was a German mathematician. He is also known by the name Adam Riese.- Life :Almost nothing is known about Ries' childhood, youth and education. It is not even possible to determine the year of his birth with certainty. The caption on the only known contemporary portrait of the...
explained the use of Arabic digits and their advantages over Roman numerals. - 1535 — Niccolo Tartaglia independently develops a method for solving depressed cubic equations but also does not publish.
- 1539 — Gerolamo CardanoGerolamo CardanoGerolamo Cardano was an Italian Renaissance mathematician, physician, astrologer and gambler...
learns Tartaglia's method for solving depressed cubics and discovers a method for depressing cubics, thereby creating a method for solving all cubics. - 1540 — Lodovico FerrariLodovico FerrariLodovico Ferrari was an Italian mathematician.Born in Milan, Italy, grandfather, Bartholomew Ferrari was forced out of Milan to Bologna. He settled in Bologna, Italy and he began his career as the servant of Gerolamo Cardano. He was extremely bright, so Cardano started teaching him mathematics...
solves the quartic equation. - 1544 — Michael StifelMichael StifelMichael Stifel or Styfel was a German monk and mathematician. He was an Augustinian who became an early supporter of Martin Luther. Stifel was later appointed professor of mathematics at Jena University...
publishes “Arithmetica integra”. - 1550 — JyeshtadevaJyeshtadevaJyeṣṭhadeva was an astronomer-mathematician of the Kerala school of astronomy and mathematics founded by Sangamagrama Madhava . He is best known as the author of Yuktibhāṣā,...
, a Kerala schoolKerala schoolKerala school may refer to*Kerala school of astronomy and mathematics, a school of mathematics and astronomy founded by Madhava of Sangamagrama in Kerala, South India which flourished between the 14th and 16th centuries CE....
mathematician, writes the “Yuktibhasa”, the world's first calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
text, which gives detailed derivations of many calculus theorems and formulae. - 1572 — Rafael BombelliRafael BombelliRafael Bombelli was an Italian mathematician.Born in Bologna, he is the author of a treatise on algebra and is a central figure in the understanding of imaginary numbers....
writes "Algebra" teatrise and uses imaginary numbers to solve cubic equations. - 1596 — Ludolf van Ceulen computes π to twenty decimal places using inscribed and circumscribed polygons.
17th century
- 17th century – Puthumana SomayajiPuthumana SomayajiPuthumana Somayaji was a 15th century mathematician from Kerala, India. He was born into the Puthumana Illam, and is believed to have been a contemporary of Vatasseri Namboodiri....
writes the "Paddhati", which presents a detailed discussion of various trigonometric series - 1614 – John NapierJohn NapierJohn Napier of Merchiston – also signed as Neper, Nepair – named Marvellous Merchiston, was a Scottish mathematician, physicist, astronomer & astrologer, and also the 8th Laird of Merchistoun. He was the son of Sir Archibald Napier of Merchiston. John Napier is most renowned as the discoverer...
discusses Napierian logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s in Mirifici Logarithmorum Canonis Descriptio, - 1617 – Henry BriggsHenry Briggs (mathematician)Henry Briggs was an English mathematician notable for changing the original logarithms invented by John Napier into common logarithms, which are sometimes known as Briggsian logarithms in his honour....
discusses decimal logarithms in Logarithmorum Chilias Prima, - 1618 – John Napier publishes the first references to eE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
in a work on logarithms. - 1619 – René DescartesRené DescartesRené Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
discovers analytic geometryAnalytic geometryAnalytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
(Pierre de FermatPierre de FermatPierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
claimed that he also discovered it independently), - 1619 – Johannes KeplerJohannes KeplerJohannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
discovers two of the Kepler-Poinsot polyhedra. - 1629 – Pierre de Fermat develops a rudimentary differential calculusDifferential calculusIn mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
, - 1634 – Gilles de RobervalGilles de RobervalGilles Personne de Roberval , French mathematician, was born at Roberval, Oise, near Beauvais, France. His name was originally Gilles Personne or Gilles Personier, that of Roberval, by which he is known, being taken from the place of his birth.Like René Descartes, he was present at the siege of La...
shows that the area under a cycloidCycloidA cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
is three times the area of its generating circle, - 1636 – Muhammad Baqir YazdiMuhammad Baqir YazdiMuhammad Baqir Yazdi was an Iranian mathematician who lived in the 16th century. He gave the pair of amicable numbers 9,363,584 and 9,437,056 many years before Euler's contribution to amicable numbers....
jointly discovered the pair of amicable numberAmicable numberAmicable numbers are two different numbers so related that the sum of the proper divisors of each is equal to the other number. A pair of amicable numbers constitutes an aliquot sequence of period 2...
s 9,363,584 and 9,437,056 along with Descartes (1636). - 1637 – Pierre de Fermat claims to have proven Fermat's Last TheoremFermat's Last TheoremIn number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
in his copy of DiophantusDiophantusDiophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
' Arithmetica, - 1637 – First use of the term imaginary numberImaginary numberAn imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
by René Descartes; it was meant to be derogatory. - 1654 – Blaise PascalBlaise PascalBlaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
and Pierre de Fermat create the theory of probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, - 1655 – John Wallis writes Arithmetica Infinitorum,
- 1658 – Christopher WrenChristopher WrenSir Christopher Wren FRS is one of the most highly acclaimed English architects in history.He used to be accorded responsibility for rebuilding 51 churches in the City of London after the Great Fire in 1666, including his masterpiece, St. Paul's Cathedral, on Ludgate Hill, completed in 1710...
shows that the length of a cycloid is four times the diameter of its generating circle, - 1665 – Isaac NewtonIsaac NewtonSir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
works on the fundamental theorem of calculusFundamental theorem of calculusThe first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
and develops his version of infinitesimal calculusInfinitesimal calculusInfinitesimal calculus is the part of mathematics concerned with finding slope of curves, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz and Isaac Newton starting in the 1660s...
, - 1668 – Nicholas MercatorNicholas MercatorNicholas Mercator , also known by his Germanic name Kauffmann, was a 17th-century mathematician....
and William Brouncker discover an infinite series for the logarithm while attempting to calculate the area under a hyperbolic segment, - 1671 – James GregoryJames Gregory (astronomer and mathematician)James Gregory FRS was a Scottish mathematician and astronomer. He described an early practical design for the reflecting telescope – the Gregorian telescope – and made advances in trigonometry, discovering infinite series representations for several trigonometric functions.- Biography :The...
develops a series expansion for the inverse-tangent function (originally discovered by MadhavaMadhava of SangamagramaMādhava of Sañgamāgrama was a prominent Kerala mathematician-astronomer from the town of Irińńālakkuţa near Cochin, Kerala, India. He is considered the founder of the Kerala School of Astronomy and Mathematics...
) - 1673 – Gottfried LeibnizGottfried LeibnizGottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
also develops his version of infinitesimal calculus, - 1675 – Isaac Newton invents an algorithm for the computation of functional rootsNewton's methodIn numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
, - 1680s – Gottfried Leibniz works on symbolic logic,
- 1691 – Gottfried Leibniz discovers the technique of separation of variables for ordinary differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, - 1693 – Edmund Halley prepares the first mortality tables statistically relating death rate to age,
- 1696 – Guillaume de L'Hôpital states his ruleL'Hôpital's ruleIn calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit...
for the computation of certain limitsLimit (mathematics)In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
, - 1696 – Jakob Bernoulli and Johann BernoulliJohann BernoulliJohann Bernoulli was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family...
solve brachistochrone problemBrachistochrone curveA Brachistochrone curve , or curve of fastest descent, is the curve between two points that is covered in the least time by a point-like body that starts at the first point with zero speed and is constrained to move along the curve to the second point, under the action of constant gravity and...
, the first result in the calculus of variationsCalculus of variationsCalculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
,
18th century
- 1706 – John MachinJohn MachinJohn Machin, , a professor of astronomy at Gresham College, London, is best known for developing a quickly converging series for Pi in 1706 and using it to compute Pi to 100 decimal places.Machin's formula is:...
develops a quickly converging inverse-tangent series for π and computes π to 100 decimal places, - 1712 – Brook TaylorBrook TaylorBrook Taylor FRS was an English mathematician who is best known for Taylor's theorem and the Taylor series.- Life and work :...
develops Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
, - 1722 – Abraham de MoivreAbraham de MoivreAbraham de Moivre was a French mathematician famous for de Moivre's formula, which links complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He was a friend of Isaac Newton, Edmund Halley, and James Stirling...
states de Moivre's formulaDe Moivre's formulaIn mathematics, de Moivre's formula , named after Abraham de Moivre, states that for any complex number x and integer n it holds that...
connecting trigonometric functionTrigonometric functionIn mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s and complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, - 1724 – Abraham De Moivre studies mortality statistics and the foundation of the theory of annuities in Annuities on Lives,
- 1730 – James StirlingJames Stirling (mathematician)James Stirling was a Scottish mathematician. The Stirling numbers and Stirling's approximation are named after him.-Biography:...
publishes The Differential Method, - 1733 – Giovanni Gerolamo Saccheri studies what geometry would be like if Euclid's fifth postulateParallel postulateIn geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
were false, - 1733 – Abraham de Moivre introduces the normal distribution to approximate the binomial distribution in probability,
- 1734 – Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
introduces the integrating factor technique for solving first-order ordinary differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, - 1735 – Leonhard Euler solves the Basel problemBasel problemThe Basel problem is a famous problem in mathematical analysis with relevance to number theory, first posed by Pietro Mengoli in 1644 and solved by Leonhard Euler in 1735. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate...
, relating an infinite series to π, - 1736 – Leonhard Euler solves the problem of the Seven bridges of KönigsbergSeven Bridges of KönigsbergThe Seven Bridges of Königsberg is a historically notable problem in mathematics. Its negative resolution by Leonhard Euler in 1735 laid the foundations of graph theory and prefigured the idea of topology....
, in effect creating graph theoryGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, - 1739 – Leonhard Euler solves the general homogeneous linear ordinary differential equation with constant coefficientsConstant coefficientsIn mathematics, constant coefficients is a term applied to differential operators, and also some difference operators, to signify that they contain no functions of the independent variables, other than constant functions. In other words, it singles out special operators, within the larger class of...
, - 1742 – Christian GoldbachChristian GoldbachChristian Goldbach was a German mathematician who also studied law. He is remembered today for Goldbach's conjecture.-Biography:...
conjectures that every even number greater than two can be expressed as the sum of two primes, now known as Goldbach's conjectureGoldbach's conjectureGoldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
, - 1748 – Maria Gaetana AgnesiMaria Gaetana AgnesiMaria Gaetana Agnesi was an Italian linguist, mathematician, and philosopher. Agnesi is credited with writing the first book discussing both differential and integral calculus. She was an honorary member of the faculty at the University of Bologna...
discusses analysis in Instituzioni Analitiche ad Uso della Gioventu Italiana, - 1761 – Thomas BayesThomas BayesThomas Bayes was an English mathematician and Presbyterian minister, known for having formulated a specific case of the theorem that bears his name: Bayes' theorem...
proves Bayes' theoremBayes' theoremIn probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
, - 1761 – Johann Heinrich LambertJohann Heinrich LambertJohann Heinrich Lambert was a Swiss mathematician, physicist, philosopher and astronomer.Asteroid 187 Lamberta was named in his honour.-Biography:...
proves that π is irrational, - 1762 – Joseph Louis LagrangeJoseph Louis LagrangeJoseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
discovers the divergence theoremDivergence theoremIn vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
, - 1789 – Jurij VegaJurij VegaBaron Jurij Bartolomej Vega was a Slovene mathematician, physicist and artillery officer.-Early life:...
improves Machin's formula and computes π to 140 decimal places, - 1794 – Jurij Vega publishes Thesaurus Logarithmorum Completus,
- 1796 – Carl Friedrich GaussCarl Friedrich GaussJohann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
proves that the regular 17-gonHeptadecagonIn geometry, a heptadecagon is a seventeen-sided polygon.-Heptadecagon construction:The regular heptadecagon is a constructible polygon, as was shown by Carl Friedrich Gauss in 1796 at the age of 19....
can be constructed using only a compass and straightedgeCompass and straightedgeCompass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass.... - 1796 – Adrien-Marie LegendreAdrien-Marie LegendreAdrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
conjectures the prime number theoremPrime number theoremIn number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
, - 1797 – Caspar WesselCaspar WesselCaspar Wessel was a Norwegian-Danish mathematician and cartographer. In 1799, Wessel was the first person to describe the complex numbers. He was the younger brother of poet and playwright Johan Herman Wessel....
associates vectors with complex numbers and studies complex number operations in geometrical terms, - 1799 – Carl Friedrich Gauss proves the fundamental theorem of algebraFundamental theorem of algebraThe fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
(every polynomial equation has a solution among the complex numbers), - 1799 – Paolo RuffiniPaolo RuffiniPaolo Ruffini was an Italian mathematician and philosopher.By 1788 he had earned university degrees in philosophy, medicine/surgery, and mathematics...
partially proves the Abel–Ruffini theoremAbel–Ruffini theoremIn algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...
that quinticQuintic equationIn mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
or higher equations cannot be solved by a general formula,
19th century
- 1801 – Disquisitiones ArithmeticaeDisquisitiones ArithmeticaeThe Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
, Carl Friedrich Gauss's number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
treatise, is published in Latin - 1805 – Adrien-Marie Legendre introduces the method of least squares for fitting a curve to a given set of observations,
- 1806 – Louis PoinsotLouis PoinsotLouis Poinsot was a French mathematician and physicist. Poinsot was the inventor of geometrical mechanics, showing how a system of forces acting on a rigid body could be resolved into a single force and a couple.-Life:...
discovers the two remaining Kepler-Poinsot polyhedra. - 1806 – Jean-Robert ArgandJean-Robert ArgandJean-Robert Argand was a gifted amateur mathematician. In 1806, while managing a bookstore in Paris, he published the idea of geometrical interpretation of complex numbers known as the Argand diagram.-Life:...
publishes proof of the Fundamental theorem of algebraFundamental theorem of algebraThe fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
and the Argand diagram, - 1807 – Joseph FourierJoseph FourierJean Baptiste Joseph Fourier was a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honour...
announces his discoveries about the trigonometric decomposition of functionsFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, - 1811 – Carl Friedrich Gauss discusses the meaning of integrals with complex limits and briefly examines the dependence of such integrals on the chosen path of integration,
- 1815 – Siméon-Denis Poisson carries out integrations along paths in the complex plane,
- 1817 – Bernard BolzanoBernard BolzanoBernhard Placidus Johann Nepomuk Bolzano , Bernard Bolzano in English, was a Bohemian mathematician, logician, philosopher, theologian, Catholic priest and antimilitarist of German mother tongue.-Family:Bolzano was the son of two pious Catholics...
presents the intermediate value theoremIntermediate value theoremIn mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
---a continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
which is negative at one point and positive at another point must be zero for at least one point in between, - 1822 – Augustin-Louis Cauchy presents the Cauchy integral theorem for integration around the boundary of a rectangle in the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, - 1824 – Niels Henrik AbelNiels Henrik AbelNiels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
partially proves the Abel–Ruffini theoremAbel–Ruffini theoremIn algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...
that the general quinticQuintic equationIn mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
or higher equations cannot be solved by a general formula involving only arithmetical operations and roots, - 1825 – Augustin-Louis Cauchy presents the Cauchy integral theorem for general integration paths—he assumes the function being integrated has a continuous derivative, and he introduces the theory of residueResidue (complex analysis)In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
s in complex analysisComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, - 1825 – Johann Peter Gustav Lejeune DirichletJohann Peter Gustav Lejeune DirichletJohann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
and Adrien-Marie Legendre prove Fermat's Last Theorem for n = 5, - 1825 – André-Marie AmpèreAndré-Marie AmpèreAndré-Marie Ampère was a French physicist and mathematician who is generally regarded as one of the main discoverers of electromagnetism. The SI unit of measurement of electric current, the ampere, is named after him....
discovers Stokes' theoremStokes' theoremIn differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
, - 1828 – George Green proves Green's theoremGreen's theoremIn mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
, - 1829 – Bolyai, GaussCarl Friedrich GaussJohann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
, and LobachevskyNikolai Ivanovich LobachevskyNikolai Ivanovich Lobachevsky was a Russian mathematician and geometer, renowned primarily for his pioneering works on hyperbolic geometry, otherwise known as Lobachevskian geometry...
invent hyperbolic non-Euclidean geometryNon-Euclidean geometryNon-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
, - 1831 – Mikhail Vasilievich OstrogradskyMikhail Vasilievich OstrogradskyMikhail Vasilyevich Ostrogradsky was an Russian / Ukrainian mathematician, mechanician and physicist...
rediscovers and gives the first proof of the divergence theorem earlier described by Lagrange, Gauss and Green, - 1832 – Évariste GaloisÉvariste GaloisÉvariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
presents a general condition for the solvability of algebraic equations, thereby essentially founding group theoryGroup theoryIn mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
and Galois theoryGalois theoryIn mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, - 1832 – Peter Dirichlet proves Fermat's Last Theorem for n = 14,
- 1835 – Peter Dirichlet proves Dirichlet's theoremDirichlet's theorem on arithmetic progressionsIn number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
about prime numbers in arithmetical progressions, - 1837 – Pierre Wantsel proves that doubling the cube and trisecting the angle are impossible with only a compass and straightedge, as well as the full completion of the problem of constructability of regular polygons
- 1841 – Karl WeierstrassKarl WeierstrassKarl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
discovers but does not publish the Laurent expansion theorem, - 1843 – Pierre-Alphonse Laurent discovers and presents the Laurent expansion theorem,
- 1843 – William HamiltonWilliam Rowan HamiltonSir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
discovers the calculus of quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s and deduces that they are non-commutative, - 1847 – George BooleGeorge BooleGeorge Boole was an English mathematician and philosopher.As the inventor of Boolean logic—the basis of modern digital computer logic—Boole is regarded in hindsight as a founder of the field of computer science. Boole said,...
formalizes symbolic logic in The Mathematical Analysis of Logic, defining what is now called Boolean algebra, - 1849 – George Gabriel StokesGeorge Gabriel StokesSir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...
shows that solitary waveSolitonIn mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s can arise from a combination of periodic waves, - 1850 – Victor Alexandre Puiseux distinguishes between poles and branch points and introduces the concept of essential singular pointsMathematical singularityIn mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
, - 1850 – George Gabriel Stokes rediscovers and proves Stokes' theorem,
- 1854 – Bernhard RiemannBernhard RiemannGeorg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
introduces Riemannian geometryRiemannian geometryRiemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, - 1854 – Arthur CayleyArthur CayleyArthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
shows that quaternions can be used to represent rotations in four-dimensional spaceSpaceSpace is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
, - 1858 – August Ferdinand MöbiusAugust Ferdinand MöbiusAugust Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
invents the Möbius stripMöbius stripThe Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
, - 1858 – Charles HermiteCharles HermiteCharles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....
solves the general quintic equation by means of elliptic and modular functions, - 1859 – Bernhard Riemann formulates the Riemann hypothesisRiemann hypothesisIn mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
which has strong implications about the distribution of prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s, - 1870 – Felix KleinFelix KleinChristian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
constructs an analytic geometry for Lobachevski's geometry thereby establishing its self-consistency and the logical independence of Euclid's fifth postulate, - 1872 – Richard DedekindRichard DedekindJulius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
invents what is now called the Dedekind Cut for defining irrational numbers, and now used for defining surreal numbers, - 1873 – Charles HermiteCharles HermiteCharles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....
proves that eE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
is transcendental, - 1873 – Georg Frobenius presents his method for finding series solutions to linear differential equations with regular singular points,
- 1874 – Georg CantorGeorg CantorGeorg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
proves that the set of all real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is uncountably infinite but the set of all real algebraic numberAlgebraic numberIn mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s is countably infinite. His proofCantor's first uncountability proofGeorg Cantor's first uncountability proof demonstrates that the set of all real numbers is uncountable. This proof differs from the more familiar proof that uses his diagonal argument...
does not use his famous diagonal argumentCantor's diagonal argumentCantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
, which he published in 1891. - 1882 – Ferdinand von LindemannFerdinand von LindemannCarl Louis Ferdinand von Lindemann was a German mathematician, noted for his proof, published in 1882, that π is a transcendental number, i.e., it is not a root of any polynomial with rational coefficients....
proves that π is transcendental and that therefore the circle cannot be squared with a compass and straightedge, - 1882 – Felix Klein invents the Klein bottleKlein bottleIn mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
, - 1895 – Diederik KortewegDiederik KortewegDiederik Johannes Korteweg was a Dutch mathematician. He is now remembered as the joint discoverer of the Korteweg–de Vries equation.-Early life and education:...
and Gustav de VriesGustav de VriesGustav de Vries was a Dutch mathematician, who is best remembered for his work on the Korteweg–de Vries equation with Diederik Korteweg. He was born on 22 January 1866 in Amsterdam, and studied at the University of Amsterdam with the distinguished physical chemist Johannes van der Waals and with...
derive the Korteweg–de Vries equationKorteweg–de Vries equationIn mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
to describe the development of long solitary water waves in a canal of rectangular cross section, - 1895 – Georg Cantor publishes a book about set theory containing the arithmetic of infinite cardinal numberCardinal numberIn mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s and the continuum hypothesisContinuum hypothesisIn mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
, - 1896 – Jacques HadamardJacques HadamardJacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
and Charles Jean de la Vallée-PoussinCharles Jean de la Vallée-PoussinCharles-Jean Étienne Gustave Nicolas de la Vallée Poussin was a Belgian mathematician. He is most well known for proving the Prime number theorem.The king of Belgium ennobled him with the title of baron.-Biography:...
independently prove the prime number theoremPrime number theoremIn number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
, - 1896 – Hermann MinkowskiHermann MinkowskiHermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
presents Geometry of numbers, - 1899 – Georg Cantor discovers a contradiction in his set theory,
- 1899 – David HilbertDavid HilbertDavid Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
presents a set of self-consistent geometric axioms in Foundations of Geometry, - 1900 – David Hilbert states his list of 23 problemsHilbert's problemsHilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
which show where some further mathematical work is needed.
20th century
- 1901 – Élie CartanÉlie CartanÉlie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
develops the exterior derivativeExterior derivativeIn differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
, - 1903 – Carle David Tolme RungeCarle David Tolmé RungeCarl David Tolmé Runge was a German mathematician, physicist, and spectroscopist.He was co-developer and co-eponym of the Runge–Kutta method , in the field of what is today known as numerical analysis.-Biography:...
presents a fast Fourier TransformFast Fourier transformA fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
algorithm, - 1903 – Edmund Georg Hermann Landau gives considerably simpler proof of the prime number theorem.
- 1908 – Ernst ZermeloErnst ZermeloErnst Friedrich Ferdinand Zermelo was a German mathematician, whose work has major implications for the foundations of mathematics and hence on philosophy. He is known for his role in developing Zermelo–Fraenkel axiomatic set theory and his proof of the well-ordering theorem.-Life:He graduated...
axiomizes set theorySet theorySet theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, thus avoiding Cantor's contradictions, - 1908 – Josip PlemeljJosip PlemeljJosip Plemelj was a Slovene mathematician, whose main contributions were to the theory of analytic functions and the application of integral equations to potential theory.- Life :...
solves the Riemann problem about the existence of a differential equation with a given monodromic group and uses Sokhotsky – Plemelj formulae, - 1912 – Luitzen Egbertus Jan BrouwerLuitzen Egbertus Jan BrouwerLuitzen Egbertus Jan Brouwer FRS , usually cited as L. E. J. Brouwer but known to his friends as Bertus, was a Dutch mathematician and philosopher, a graduate of the University of Amsterdam, who worked in topology, set theory, measure theory and complex analysis.-Biography:Early in his career,...
presents the Brouwer fixed-point theorem, - 1912 – Josip Plemelj publishes simplified proof for the Fermat's Last Theorem for exponent n = 5,
- 1919 – Viggo BrunViggo BrunViggo Brun was a Norwegian mathematician.He studied at the University of Oslo and began research at the University of Göttingen in 1910. In 1923, Brun became a professor at the Technical University in Trondheim and in 1946 a professor at the University of Oslo...
defines Brun's constant B2 for twin primeTwin primeA twin prime is a prime number that differs from another prime number by two. Except for the pair , this is the smallest possible difference between two primes. Some examples of twin prime pairs are , , , , and...
s, - 1928 – John von NeumannJohn von NeumannJohn von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
begins devising the principles of game theoryGame theoryGame theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
and proves the minimax theorem, - 1930 – Casimir Kuratowski shows that the three-cottage problem has no solution,
- 1931 – Kurt GödelKurt GödelKurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
proves his incompleteness theorem which shows that every axiomatic system for mathematics is either incomplete or inconsistent, - 1931 – Georges de RhamGeorges de RhamGeorges de Rham was a Swiss mathematician, known for his contributions to differential topology.He studied at the University of Lausanne and then in Paris for a doctorate, becoming a lecturer in Lausanne in 1931; where he held positions until retirement in 1971; he held positions in Geneva in...
develops theorems in cohomologyCohomologyIn mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
and characteristic classCharacteristic classIn mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es, - 1933 – Karol BorsukKarol BorsukKarol Borsuk was a Polish mathematician.His main interest was topology.Borsuk introduced the theory of absolute retracts and absolute neighborhood retracts , and the cohomotopy groups, later called Borsuk-Spanier cohomotopy groups. He also founded the so called Shape theory...
and Stanislaw Ulam present the Borsuk-Ulam antipodal-point theorem, - 1933 – Andrey Nikolaevich Kolmogorov publishes his book Basic notions of the calculus of probability (Grundbegriffe der Wahrscheinlichkeitsrechnung) which contains an axiomatization of probability based on measure theory,
- 1940 – Kurt Gödel shows that neither the continuum hypothesisContinuum hypothesisIn mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
nor the axiom of choice can be disproven from the standard axioms of set theory, - 1942 – G.C. Danielson and Cornelius LanczosCornelius LanczosCornelius Lanczos Löwy Kornél was a Hungarian-Jewish mathematician and physicist, who was born on February 2, 1893, and died on June 25, 1974....
develop a Fast Fourier TransformFast Fourier transformA fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
algorithm, - 1943 – Kenneth Levenberg proposes a method for nonlinear least squares fitting,
- 1945 – Stephen Cole KleeneStephen Cole KleeneStephen Cole Kleene was an American mathematician who helped lay the foundations for theoretical computer science...
introduces realizabilityRealizabilityRealizability is a part of proof theory which can be used to handle information about formulas instead of about the proofs of formulas. A natural number n is said to realize a statement in the language of arithmetic of natural numbers...
, - 1945 - Saunders Mac LaneSaunders Mac LaneSaunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
and Samuel EilenbergSamuel EilenbergSamuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
start category theoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions... - 1945 - Norman SteenrodNorman SteenrodNorman Earl Steenrod was a preeminent mathematician most widely known for his contributions to the field of algebraic topology.-Life:...
and Samuel EilenbergSamuel EilenbergSamuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
give the Eilenberg–Steenrod axioms for (co-)homology - 1948 – John von Neumann mathematically studies self-reproducing machinesSelf-replicating machineA self-replicating machine is an artificial construct that is theoretically capable of autonomously manufacturing a copy of itself using raw materials taken from its environment, thus exhibiting self-replication in a way analogous to that found in nature. The concept of self-replicating machines...
, - 1949 – John von Neumann computes π to 2,037 decimal places using ENIACENIACENIAC was the first general-purpose electronic computer. It was a Turing-complete digital computer capable of being reprogrammed to solve a full range of computing problems....
, - 1950 – Stanislaw Ulam and John von Neumann present cellular automata dynamical systems,
- 1953 – Nicholas MetropolisNicholas MetropolisNicholas Constantine Metropolis was a Greek American physicist.-Work:Metropolis received his B.Sc. and Ph.D. degrees in physics at the University of Chicago...
introduces the idea of thermodynamic simulated annealingSimulated annealingSimulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
algorithms, - 1955 – H. S. M. Coxeter et al. publish the complete list of uniform polyhedronUniform polyhedronA uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
, - 1955 – Enrico FermiEnrico FermiEnrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...
, John PastaJohn PastaJohn R. Pasta was a computer scientist who is remembered today for the Fermi–Pasta–Ulam experiment, a result much discussed among physicists and researchers in dynamical systems and chaos theory, and as the head of the department of Computer Science at the University of Illinois at...
, and Stanislaw Ulam numerically study a nonlinear spring model of heat conduction and discover solitary wave type behavior, - 1956 – Noam ChomskyNoam ChomskyAvram Noam Chomsky is an American linguist, philosopher, cognitive scientist, and activist. He is an Institute Professor and Professor in the Department of Linguistics & Philosophy at MIT, where he has worked for over 50 years. Chomsky has been described as the "father of modern linguistics" and...
describes an hierarchyChomsky hierarchyWithin the field of computer science, specifically in the area of formal languages, the Chomsky hierarchy is a containment hierarchy of classes of formal grammars....
of formal languagesFormal languageA formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
, - 1958 - Alexander GrothendieckAlexander GrothendieckAlexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
's proof of the Grothendieck-Riemann-Roch theorem is published - 1960 – C. A. R. HoareC. A. R. HoareSir Charles Antony Richard Hoare , commonly known as Tony Hoare or C. A. R. Hoare, is a British computer scientist best known for the development of Quicksort, one of the world's most widely used sorting algorithms...
invents the quicksort algorithm, - 1960 – Irving S. ReedIrving S. ReedIrving Stoy Reed is a mathematician and engineer. He is best known for co-inventing a class of algebraic error-correcting and error-detecting codes known as Reed-Solomon codes in collaboration with Gustave Solomon...
and Gustave SolomonGustave SolomonGustave Solomon was a mathematician and engineer who was one of the founders of the algebraic theory of error-correction. He received Ph.D. in Mathematics at MIT in 1956 under direction of Kenkichi Iwasawa....
present the Reed-Solomon error-correcting code, - 1961 – Daniel ShanksDaniel ShanksDaniel Shanks was an American mathematician who worked primarily in numerical analysis and number theory. He is best known as the first to compute π to 100,000 decimal places, and for his book Solved and Unsolved Problems in Number Theory.-Life and education:Dan Shanks was born on January 17,...
and John WrenchJohn WrenchJohn William Wrench, Jr. was an American mathematician who worked primarily in numerical analysis. He was a pioneer in using computers for mathematical calculations, and is noted for work done with Daniel Shanks to calculate the mathematical constant pi to 100,000 decimal places.-Life and...
compute π to 100,000 decimal places using an inverse-tangent identity and an IBM-7090 computer, - 1962 – Donald MarquardtDonald MarquardtDonald W. Marquardt was an American statistician, the rediscoverer of the Levenberg–Marquardt nonlinear least squares fitting algorithm....
proposes the Levenberg–Marquardt nonlinear least squares fitting algorithm, - 1963 – Paul CohenPaul Cohen (mathematician)Paul Joseph Cohen was an American mathematician best known for his proof of the independence of the continuum hypothesis and the axiom of choice from Zermelo–Fraenkel set theory, the most widely accepted axiomatization of set theory.-Early years:Cohen was born in Long Branch, New Jersey, into a...
uses his technique of forcingForcing (mathematics)In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
to show that neither the continuum hypothesis nor the axiom of choice can be proven from the standard axioms of set theory, - 1963 – Martin KruskalMartin KruskalMartin David Kruskal was an American mathematician and physicist. He made fundamental contributions in many areas of mathematics and science, ranging from plasma physics to general relativity and from nonlinear analysis to asymptotic analysis...
and Norman ZabuskyNorman ZabuskyNorman J. Zabusky is an American physicist, who is noted for the discovery of the soliton in the Korteweg–de Vries equation, in work completed with Martin Kruskal. This result early in his career was followed by an extensive body of work in computational fluid dynamics, which led him more...
analytically study the Fermi-Pasta-Ulam heat conduction problem in the continuum limit and find that the KdV equation governs this system, - 1963 – meteorologist and mathematician Edward Norton LorenzEdward Norton LorenzEdward Norton Lorenz was an American mathematician and meteorologist, and a pioneer of chaos theory. He discovered the strange attractor notion and coined the term butterfly effect.-Biography:...
published solutions for a simplified mathematical model of atmospheric turbulence – generally known as chaotic behaviour and strange attractors or Lorenz AttractorLorenz attractorThe Lorenz attractor, named for Edward N. Lorenz, is an example of a non-linear dynamic system corresponding to the long-term behavior of the Lorenz oscillator. The Lorenz oscillator is a 3-dimensional dynamical system that exhibits chaotic flow, noted for its lemniscate shape...
– also the Butterfly EffectButterfly effectIn chaos theory, the butterfly effect is the sensitive dependence on initial conditions; where a small change at one place in a nonlinear system can result in large differences to a later state...
, - 1965 – Iranian mathematician Lotfi Asker ZadehLotfi Asker ZadehLotfali Askar Zadeh , better known as Lotfi A. Zadeh, is a mathematician, electrical engineer, computer scientist, artifical intelligence researcher and professor emeritus of computer science at the University of California, Berkeley...
founded fuzzy setFuzzy setFuzzy sets are sets whose elements have degrees of membership. Fuzzy sets were introduced simultaneously by Lotfi A. Zadeh and Dieter Klaua in 1965 as an extension of the classical notion of set. In classical set theory, the membership of elements in a set is assessed in binary terms according to...
theory as an extension of the classical notion of set and he founded the field of Fuzzy MathematicsFuzzy mathematicsFuzzy mathematics forms a branch of mathematics related to fuzzy set theory and fuzzy logic. It started in 1965 after the publication of Lotfi Asker Zadeh's seminal work Fuzzy sets. A fuzzy subset A of a set X is a function A:X→L, where L is the interval [0,1]. This function is also called a...
, - 1965 – Martin Kruskal and Norman Zabusky numerically study colliding solitary wavesSolitonIn mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
in plasmasPlasma (physics)In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...
and find that they do not disperse after collisions, - 1965 – James CooleyJames CooleyDr. James W. Cooley is an American mathematician. James William Cooley received a B.A. degree in 1949 from Manhattan College, Bronx, NY, an M.A. degree in 1951 from Columbia University, New York, NY, and a Ph.D. degree in 1961 in applied mathematics from Columbia University...
and John TukeyJohn TukeyJohn Wilder Tukey ForMemRS was an American statistician.- Biography :Tukey was born in New Bedford, Massachusetts in 1915, and obtained a B.A. in 1936 and M.Sc. in 1937, in chemistry, from Brown University, before moving to Princeton University where he received a Ph.D...
present an influential Fast Fourier Transform algorithm, - 1966 – E.J. Putzer presents two methods for computing the exponential of a matrixMatrix exponentialIn mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
in terms of a polynomial in that matrix, - 1966 – Abraham RobinsonAbraham RobinsonAbraham Robinson was a mathematician who is most widely known for development of non-standard analysis, a mathematically rigorous system whereby infinitesimal and infinite numbers were incorporated into mathematics....
presents Non-standard analysisNon-standard analysisNon-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
. - 1967 – Robert LanglandsRobert LanglandsRobert Phelan Langlands is a mathematician, best known as the founder of the Langlands program. He is an emeritus professor at the Institute for Advanced Study...
formulates the influential Langlands programLanglands programThe Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
of conjectures relating number theory and representation theory, - 1968 – Michael AtiyahMichael AtiyahSir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
and Isadore SingerIsadore SingerIsadore Manuel Singer is an Institute Professor in the Department of Mathematics at the Massachusetts Institute of Technology...
prove the Atiyah-Singer index theorem about the index of elliptic operatorElliptic operatorIn the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
s, - 1973 – Lotfi Zadeh founded the field of fuzzy logicFuzzy logicFuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
, - 1975 – Benoît MandelbrotBenoît MandelbrotBenoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child...
publishes Les objets fractals, forme, hasard et dimension, - 1976 – Kenneth AppelKenneth AppelKenneth Ira Appel is a mathematician who in 1976, with colleague Wolfgang Haken at the University of Illinois at Urbana-Champaign, solved one of the most famous problems in mathematics, the four-color theorem...
and Wolfgang HakenWolfgang HakenWolfgang Haken is a mathematician who specializes in topology, in particular 3-manifolds.In 1976 together with colleague Kenneth Appel at the University of Illinois at Urbana-Champaign, Haken solved one of the most famous problems in mathematics, the four-color theorem...
use a computer to prove the Four color theoremFour color theoremIn mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
, - 1981 – Richard FeynmanRichard FeynmanRichard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
gives an influential talk "Simulating Physics with Computers" (in 1980 Yuri Manin proposed the same idea about quantum computations in "Computable and Uncomputable" (in Russian)), - 1983 – Gerd FaltingsGerd FaltingsGerd Faltings is a German mathematician known for his work in arithmetic algebraic geometry.From 1972 to 1978, he studied mathematics and physics at the University of Münster. In 1978 he received his PhD in mathematics and in 1981 he got the venia legendi in mathematics, both from the University...
proves the Mordell conjecture and thereby shows that there are only finitely many whole number solutions for each exponent of Fermat's Last Theorem, - 1983 – the classification of finite simple groupsClassification of finite simple groupsIn mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
, a collaborative work involving some hundred mathematicians and spanning thirty years, is completed, - 1985 – Louis de Branges de BourciaLouis de Branges de BourciaLouis de Branges de Bourcia is a French-American mathematician. He is the Edward C. Elliott Distinguished Professor of Mathematics at Purdue University in West Lafayette, Indiana. He is best known for proving the long-standing Bieberbach conjecture in 1984, now called de Branges' theorem...
proves the Bieberbach conjecture, - 1987 – Yasumasa KanadaYasumasa Kanadais a Japanese mathematician most known for his numerous world records over the past three decades for calculating digits of π. He has set the record 11 of the past 21 times....
, David BaileyDavid H. BaileyDavid Harold Bailey is a mathematician and computer scientist. He received his B.S. in mathematics from Brigham Young University in 1972 and his Ph.D. in mathematics from Stanford University in 1976...
, Jonathan BorweinJonathan BorweinJonathan Michael Borwein is a Scottish mathematician who holds an appointment as Laureate Professor of mathematics at the University of Newcastle, Australia. Noted for his prolific and creative work throughout the international mathematical community, he is a close associate of David H...
, and Peter BorweinPeter BorweinPeter Benjamin Borwein is a Canadian mathematicianand a professor at Simon Fraser University. He is known as a co-discoverer of the Bailey-Borwein-Plouffe algorithm for computing π.-First interest in mathematics:...
use iterative modular equation approximations to elliptic integrals and a NEC SX-2 supercomputerSupercomputerA supercomputer is a computer at the frontline of current processing capacity, particularly speed of calculation.Supercomputers are used for highly calculation-intensive tasks such as problems including quantum physics, weather forecasting, climate research, molecular modeling A supercomputer is a...
to compute π to 134 million decimal places, - 1991 – Alain ConnesAlain ConnesAlain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
and John W. Lott develop non-commutative geometry, - 1992 – David DeutschDavid DeutschDavid Elieser Deutsch, FRS is an Israeli-British physicist at the University of Oxford. He is a non-stipendiary Visiting Professor in the Department of Atomic and Laser Physics at the Centre for Quantum Computation in the Clarendon Laboratory of the University of Oxford...
and Richard JozsaRichard JozsaRichard Jozsa is the holder of the Leigh Trapnell Chair in Quantum Physics at the University of Cambridge. His research area is quantum information science; a pioneer of this field, he is the co-author of the Deutsch-Jozsa quantum algorithm and one of the co-inventors of quantum teleportation...
developes Deutsch–Jozsa algorithm, one of the first examples of a quantum algorithmQuantum algorithmIn quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a...
that is exponentially faster than any possible deterministic classical algorithm. - 1994 – Andrew WilesAndrew WilesSir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
proves part of the Taniyama-Shimura conjecture and thereby proves Fermat's Last TheoremFermat's Last TheoremIn number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
, - 1994 – Peter ShorPeter ShorPeter Williston Shor is an American professor of applied mathematics at MIT, most famous for his work on quantum computation, in particular for devising Shor's algorithm, a quantum algorithm for factoring exponentially faster than the best currently-known algorithm running on a classical...
formulates Shor's algorithmShor's algorithmShor's algorithm, named after mathematician Peter Shor, is a quantum algorithm for integer factorization formulated in 1994...
, a quantum algorithmQuantum algorithmIn quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a...
for integer factorizationInteger factorizationIn number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
, - 1998 – Thomas Callister HalesThomas Callister HalesThomas Callister Hales is an American mathematician. He is known for his 1998 computer-aided proof of the Kepler conjecture, a centuries-old problem in discrete geometry which states that the most space-efficient way to pack spheres is in a pyramid shape...
(almost certainly) proves the Kepler conjectureKepler conjectureThe Kepler conjecture, named after the 17th-century German astronomer Johannes Kepler, is a mathematical conjecture about sphere packing in three-dimensional Euclidean space. It says that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic...
, - 1999 – the full Taniyama-Shimura conjecture is proved,
- 2000 – the Clay Mathematics InstituteClay Mathematics InstituteThe Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...
proposes the seven Millennium Prize ProblemsMillennium Prize ProblemsThe Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. As of September 2011, six of the problems remain unsolved. A correct solution to any of the problems results in a US$1,000,000 prize being awarded by the institute...
of unsolved important classic mathematical questions.
21st century
- 2002 – Manindra AgrawalManindra AgrawalManindra Agrawal is a professor at the department of computer science and engineering and the Dean of Resource, Planning and Generation at the Indian Institute of Technology, Kanpur. He is also the recipient of the first Infosys Prize for Mathematics.-Early life:Manindra Agrawal obtained a...
, Nitin SaxenaNitin SaxenaNitin Saxena is an Indian scientist, active in the fields of mathematics and theoretical computer science. His research focuses on topics in computational complexity, especially algebraic approaches....
, and Neeraj KayalNeeraj KayalNeeraj Kayal is an Indian computer scientist. Kayal was born and raised in Guwahati, India.Kayal graduated with a B.Tech from the Computer Science Department of the Indian Institute of Technology, Kanpur , India in 2002...
of IIT Kanpur present an unconditional deterministic polynomial time algorithm to determine whether a given number is primePrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
(the AKS primality testAKS primality testThe AKS primality test is a deterministic primality-proving algorithm created and published by three Indian Institute of Technology Kanpur computer scientists, Manindra Agrawal, Neeraj Kayal, and Nitin Saxena, on August 6, 2002, in a paper titled "PRIMES is in P"...
), - 2002 – Yasumasa KanadaYasumasa Kanadais a Japanese mathematician most known for his numerous world records over the past three decades for calculating digits of π. He has set the record 11 of the past 21 times....
, Y. Ushiro, Hisayasu Kuroda, Makoto Kudoh and a team of nine more compute π to 1241.1 billion digits using a HitachiHitachi, Ltd.is a Japanese multinational conglomerate headquartered in Marunouchi 1-chome, Chiyoda, Tokyo, Japan. The company is the parent of the Hitachi Group as part of the larger DKB Group companies...
64-node supercomputerSupercomputerA supercomputer is a computer at the frontline of current processing capacity, particularly speed of calculation.Supercomputers are used for highly calculation-intensive tasks such as problems including quantum physics, weather forecasting, climate research, molecular modeling A supercomputer is a...
, - 2002 – Preda MihăilescuPreda MihailescuPreda V. Mihăilescu is a Romanian mathematician, best known for his proof of Catalan's conjecture.Born in Bucharest, he is the brother of Vintilă Mihăilescu. After leaving Romania in 1973, he settled in Switzerland. He studied mathematics and computer science in Zürich, receiving his Ph.D. from...
proves Catalan's conjecture, - 2003 – Grigori PerelmanGrigori PerelmanGrigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
proves the Poincaré conjecturePoincaré conjectureIn mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
, - 2007 – a team of researchers throughout North America and Europe used networks of computers to map E8E8 (mathematics)In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
. - 2009 - Fundamental lemma (Langlands program) had been proofedMathematical proofIn mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
by Ngo Bao ChauNgo Bao ChauNgô Bảo Châu is a Vietnamese and French mathematician at the University of Chicago, best known for proving the fundamental lemma for automorphic forms proposed by Robert Langlands and Diana Shelstad. He is the first Vietnamese to receive the Fields Medal.- Biography :Chau was born in 1972, the...
.