
Simulated annealing
Encyclopedia
Simulated annealing is a generic probabilistic metaheuristic
for the global optimization
problem of locating a good approximation to the global optimum
of a given function
in a large search space
. It is often used when the search space is discrete (e.g., all tours that visit a given set of cities). For certain problems, simulated annealing may be more efficient than exhaustive enumeration — provided that the goal is merely to find an acceptably good solution in a fixed amount of time, rather than the best possible solution.
The name and inspiration come from annealing
in metallurgy
, a technique involving heating and controlled cooling of a material to increase the size of its crystal
s and reduce their defects
. The heat causes the atom
s to become unstuck from their initial positions (a local minimum of the internal energy
) and wander randomly through states of higher energy; the slow cooling gives them more chances of finding configurations with lower internal energy than the initial one.
By analogy with this physical process, each step of the SA algorithm attempts to replace the current solution by a random solution (chosen according to a candidate distribution, often constructed to sample from solutions near the current solution). The new solution may then be accepted with a probability that depends both on the difference between the corresponding function values and also on a global parameter T (called the temperature), that is gradually decreased during the process. The dependency is such that the choice between the previous and current solution is almost random when T is large, but increasingly selects the better or "downhill" solution (for a minimization problem) as T goes to zero. The allowance for "uphill" moves potentially saves the method from becoming stuck at local optima
—which are the bane of greedier
methods.
The method was independently described by Scott Kirkpatrick, C. Daniel Gelatt and Mario P. Vecchi in 1983, and by Vlado Černý in 1985. The method is an adaptation of the Metropolis-Hastings algorithm
, a Monte Carlo method
to generate sample states of a thermodynamic system, invented by M.N. Rosenbluth
in a paper by N. Metropolis
et al. in 1953.
of some physical system
, and the function E(s) to be minimized is analogous to the internal energy
of the system in that state. The goal is to bring the system, from an arbitrary initial state, to a state with the minimum possible energy.
of the cities to be visited. The neighbours of some particular permutation are the permutations that are produced for example by interchanging a pair of adjacent cities. The action taken to alter the solution in order to find neighbouring solutions is called "move" and different "moves" give different neighbours. These moves usually result in minimal alterations of the solution, as the previous example depicts, in order to help an algorithm to optimize the solution to the maximum extent and also to retain the already optimum parts of the solution and affect only the suboptimum parts. In the previous example, the parts of the solution are the parts of the tour.
Searching for neighbours to a state is fundamental to optimization because the final solution will come after a tour of successive neighbours. Simple heuristic
s move by finding best neighbour after best neighbour and stop when they have reached a solution which has no neighbours that are better solutions. The problem with this approach is that a solution that does not have any immediate neighbours that are better solutions is not necessarily the optimum. It would be the optimum if it was shown that any kind of alteration of the solution does not give a better solution and not just a particular kind of alteration. For this reason it is said that simple heuristic
s can only reach local optima
and not the global optimum
. Metaheuristics, although they also optimize through the neighbourhood approach, differ from heuristics in that they can move through neighbours that are worse solutions than the current solution. Simulated Annealing in particular doesn't even try to find the best neighbour. The reason for this is that the search can no longer stop in a local optimum and in theory, if the metaheuristic can run for an infinite amount of time, the global optimum will be found.
 to a candidate new state
to a candidate new state 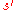 is specified by an acceptance probability function
is specified by an acceptance probability function  , that depends on the energies
, that depends on the energies 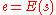 and
and  of the two states, and on a global time-varying parameter
of the two states, and on a global time-varying parameter  called the temperature.
called the temperature.
States with a smaller energy are better than those with a greater energy.
The probability function must be positive even when
must be positive even when 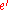 is greater than
is greater than  . This feature prevents the method from becoming stuck at a local minimum that is worse than the global one.
. This feature prevents the method from becoming stuck at a local minimum that is worse than the global one.
When tends to zero, the probability
tends to zero, the probability 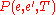 must tend to zero if
must tend to zero if  and to a positive value otherwise. For sufficiently small values of
and to a positive value otherwise. For sufficiently small values of  , the system will then increasingly favor moves that go "downhill" (i.e., to lower energy values), and avoid those that go "uphill." With
, the system will then increasingly favor moves that go "downhill" (i.e., to lower energy values), and avoid those that go "uphill." With  the procedure reduces to the greedy algorithm
the procedure reduces to the greedy algorithm
, which makes only the downhill transitions.
In the original description of SA, the probability was equal to 1 when
was equal to 1 when  — i.e., the procedure always moved downhill when it found a way to do so, irrespective of the temperature. Many descriptions and implementations of SA still take this condition as part of the method's definition. However, this condition is not essential for the method to work, and one may argue that it is both counterproductive and contrary to the method's principle.
— i.e., the procedure always moved downhill when it found a way to do so, irrespective of the temperature. Many descriptions and implementations of SA still take this condition as part of the method's definition. However, this condition is not essential for the method to work, and one may argue that it is both counterproductive and contrary to the method's principle.
The function is usually chosen so that the probability of accepting a move decreases when the difference
function is usually chosen so that the probability of accepting a move decreases when the difference
 increases—that is, small uphill moves are more likely than large ones. However, this requirement is not strictly necessary, provided that the above requirements are met.
increases—that is, small uphill moves are more likely than large ones. However, this requirement is not strictly necessary, provided that the above requirements are met.
Given these properties, the temperature plays a crucial role in controlling the evolution of the state
plays a crucial role in controlling the evolution of the state  of the system vis-a-vis its sensitivity to the variations of system energies. To be precise, for a large
of the system vis-a-vis its sensitivity to the variations of system energies. To be precise, for a large  , the evolution of
, the evolution of  is sensitive to coarser energy variations, while it is sensitive to finer energy variations when
is sensitive to coarser energy variations, while it is sensitive to finer energy variations when  is small.
is small.
 set to a high value (or infinity), and then it is decreased at each step following some annealing schedule—which may be specified by the user, but must end with
set to a high value (or infinity), and then it is decreased at each step following some annealing schedule—which may be specified by the user, but must end with  towards the end of the allotted time budget. In this way, the system is expected to wander initially towards a broad region of the search space containing good solutions, ignoring small features of the energy function; then drift towards low-energy regions that become narrower and narrower; and finally move downhill according to the steepest descent heuristic.
towards the end of the allotted time budget. In this way, the system is expected to wander initially towards a broad region of the search space containing good solutions, ignoring small features of the energy function; then drift towards low-energy regions that become narrower and narrower; and finally move downhill according to the steepest descent heuristic.
For any given finite problem, the probability that the simulated annealing algorithm terminates with the global optimal
solution approaches 1 as the annealing schedule is extended. This theoretical result, however, is not particularly helpful, since the time required to ensure a significant probability of success will usually exceed the time required for a complete search
of the solution space.
presents the simulated annealing heuristic as described above. It starts from a state s0 and continues to either a maximum of kmax steps or until a state with an energy of emax or less is found. In the process, the call neighbour(s) should generate a randomly chosen neighbour of a given state s; the call random should return a random value in the range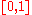 . The annealing schedule is defined by the call temp(r), which should yield the temperature to use, given the fraction r of the time budget that has been expended so far.
. The annealing schedule is defined by the call temp(r), which should yield the temperature to use, given the fraction r of the time budget that has been expended so far.
Pedantically speaking, the "pure" SA algorithm does not keep track of the best solution found so far: it does not use the variables sbest and ebest, it lacks the second if inside the loop, and, at the end, it returns the current state s instead of sbest. While remembering the best state is a standard technique in optimization that can be used in any metaheuristic
, it does not have an analogy with physical annealing — since a physical system can "store" a single state only.
Even more pedantically speaking, saving the best state is not necessarily an improvement, since one may have to specify a smaller kmax in order to compensate for the higher cost per iteration and since there is a good probability that sbest equals s in the final iteration anyway. However, the step sbest ← snew happens only on a small fraction of the moves. Therefore, the optimization is usually worthwhile, even when state-copying is an expensive operation.
. These choices can have a significant impact on the method's effectiveness. Unfortunately, there are no choices of these parameters that will be good for all problems, and there is no general way to find the best choices for a given problem. The following sections give some general guidelines.
, whose vertices are all possible states, and whose edges are the candidate moves. An essential requirement for the neighbour function is that it must provide a sufficiently short path on this graph from the initial state to any state which may be the global optimum. (In other words, the diameter of the search graph must be small.) In the traveling salesman example above, for instance, the search space for cities has
cities has 
= 2,432,902,008,176,640,000 (2.4 quintillion) states; yet the neighbour generator function that swaps two consecutive cities can get from any state (tour) to any other state in at most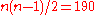 steps.
steps.
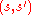 of the search graph, one defines a transition probability, which is the probability that the SA algorithm will move to state
of the search graph, one defines a transition probability, which is the probability that the SA algorithm will move to state 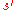 when its current state is
when its current state is  . This probability depends on the current temperature as specified by temp, by the order in which the candidate moves are generated by the neighbour function, and by the acceptance probability function P. (Note that the transition probability is not simply
. This probability depends on the current temperature as specified by temp, by the order in which the candidate moves are generated by the neighbour function, and by the acceptance probability function P. (Note that the transition probability is not simply 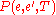 , because the candidates are tested serially.)
, because the candidates are tested serially.)
In the formulation of the method by Kirkpatrick et al., the acceptance probability function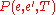 was defined as 1 if
was defined as 1 if  , and
, and  otherwise. This formula was superficially justified by analogy with the transitions of a physical system; it corresponds to the Metropolis-Hastings algorithm
otherwise. This formula was superficially justified by analogy with the transitions of a physical system; it corresponds to the Metropolis-Hastings algorithm
, in the case where the proposal distribution of Metropolis-Hastings is symmetric. However, this acceptance probability is often used for simulated annealing even when the neighbour function, which is analogous to the proposal distribution in Metropolis-Hastings, is not symmetric, or not probabilistic at all. As a result, the transition probabilities of the simulated annealing algorithm do not correspond to the transitions of the analogous physical system, and the long-term distribution of states at a constant temperature need not bear any resemblance to the thermodynamic equilibrium distribution over states of that physical system, at any temperature. Nevertheless, most descriptions of SA assume the original acceptance function, which is probably hard-coded in many implementations of SA.
need not bear any resemblance to the thermodynamic equilibrium distribution over states of that physical system, at any temperature. Nevertheless, most descriptions of SA assume the original acceptance function, which is probably hard-coded in many implementations of SA.
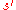 is likely to be similar to that of the current state. This heuristic
is likely to be similar to that of the current state. This heuristic
(which is the main principle of the Metropolis-Hastings algorithm
) tends to exclude "very good" candidate moves as well as "very bad" ones; however, the latter are usually much more common than the former, so the heuristic is generally quite effective.
In the traveling salesman problem above, for example, swapping two consecutive cities in a low-energy tour is expected to have a modest effect on its energy (length); whereas swapping two arbitrary cities is far more likely to increase its length than to decrease it. Thus, the consecutive-swap neighbour generator is expected to perform better than the arbitrary-swap one, even though the latter could provide a somewhat shorter path to the optimum (with swaps, instead of
swaps, instead of 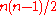 ).
).
A more precise statement of the heuristic is that one should try first candidate states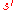 for which
for which 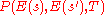 is large. For the "standard" acceptance function
is large. For the "standard" acceptance function  above, it means that
above, it means that  is on the order of
is on the order of  or less. Thus, in the traveling salesman example above, one could use a neighbour function that swaps two random cities, where the probability of choosing a city pair vanishes as their distance increases beyond
or less. Thus, in the traveling salesman example above, one could use a neighbour function that swaps two random cities, where the probability of choosing a city pair vanishes as their distance increases beyond  .
.
basins" of the energy function may trap the SA algorithm with high probability (roughly proportional to the number of states in the basin) and for a very long time (roughly exponential on the energy difference between the surrounding states and the bottom of the basin).
As a rule, it is impossible to design a candidate generator that will satisfy this goal and also prioritize candidates with similar energy. On the other hand, one can often vastly improve the efficiency of SA by relatively simple changes to the generator. In the traveling salesman problem, for instance, it is not hard to exhibit two tours ,
,  , with nearly equal lengths, such that (0)
, with nearly equal lengths, such that (0)  is optimal, (1) every sequence of city-pair swaps that converts
is optimal, (1) every sequence of city-pair swaps that converts  to
to  goes through tours that are much longer than both, and (2)
goes through tours that are much longer than both, and (2)  can be transformed into
can be transformed into  by flipping (reversing the order of) a set of consecutive cities. In this example,
by flipping (reversing the order of) a set of consecutive cities. In this example,  and
and  lie in different "deep basins" if the generator performs only random pair-swaps; but they will be in the same basin if the generator performs random segment-flips.
lie in different "deep basins" if the generator performs only random pair-swaps; but they will be in the same basin if the generator performs random segment-flips.
at all times. Unfortunately, the relaxation time—the time one must wait for the equilibrium to be restored after a change in temperature—strongly depends on the "topography" of the energy function and on the current temperature. In the SA algorithm, the relaxation time also depends on the candidate generator, in a very complicated way. Note that all these parameters are usually provided as black box functions
to the SA algorithm.
Therefore, in practice the ideal cooling rate cannot be determined beforehand, and should be empirically adjusted for each problem. The variant of SA known as thermodynamic simulated annealing tries to avoid this problem by dispensing with the cooling schedule, and instead automatically adjusting the temperature at each step based on the energy difference between the two states, according to the laws of thermodynamics.
Metaheuristic
In computer science, metaheuristic designates a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. Metaheuristics make few or no assumptions about the problem being optimized and can search very large spaces...
for the global optimization
Global optimization
Global optimization is a branch of applied mathematics and numerical analysis that deals with the optimization of a function or a set of functions to some criteria.- General :The most common form is the minimization of one real-valued function...
problem of locating a good approximation to the global optimum
Global optimum
In mathematics, a global optimum is a selection from a given domain which yields either the highest value or lowest value , when a specific function is applied. For example, for the function...
of a given function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
in a large search space
Search space
Search space may refer to one of the following.*In optimization, the domain of the function to be optimized*In search algorithms of computer science, the set of all possible solutions...
. It is often used when the search space is discrete (e.g., all tours that visit a given set of cities). For certain problems, simulated annealing may be more efficient than exhaustive enumeration — provided that the goal is merely to find an acceptably good solution in a fixed amount of time, rather than the best possible solution.
The name and inspiration come from annealing
Annealing (metallurgy)
Annealing, in metallurgy and materials science, is a heat treatment wherein a material is altered, causing changes in its properties such as strength and hardness. It is a process that produces conditions by heating to above the recrystallization temperature, maintaining a suitable temperature, and...
in metallurgy
Metallurgy
Metallurgy is a domain of materials science that studies the physical and chemical behavior of metallic elements, their intermetallic compounds, and their mixtures, which are called alloys. It is also the technology of metals: the way in which science is applied to their practical use...
, a technique involving heating and controlled cooling of a material to increase the size of its crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
s and reduce their defects
Crystallographic defect
Crystalline solids exhibit a periodic crystal structure. The positions of atoms or molecules occur on repeating fixed distances, determined by the unit cell parameters. However, the arrangement of atom or molecules in most crystalline materials is not perfect...
. The heat causes the atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s to become unstuck from their initial positions (a local minimum of the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
) and wander randomly through states of higher energy; the slow cooling gives them more chances of finding configurations with lower internal energy than the initial one.
By analogy with this physical process, each step of the SA algorithm attempts to replace the current solution by a random solution (chosen according to a candidate distribution, often constructed to sample from solutions near the current solution). The new solution may then be accepted with a probability that depends both on the difference between the corresponding function values and also on a global parameter T (called the temperature), that is gradually decreased during the process. The dependency is such that the choice between the previous and current solution is almost random when T is large, but increasingly selects the better or "downhill" solution (for a minimization problem) as T goes to zero. The allowance for "uphill" moves potentially saves the method from becoming stuck at local optima
Local optimum
Local optimum is a term in applied mathematics and computer science.A local optimum of a combinatorial optimization problem is a solution that is optimal within a neighboring set of solutions...
—which are the bane of greedier
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
methods.
The method was independently described by Scott Kirkpatrick, C. Daniel Gelatt and Mario P. Vecchi in 1983, and by Vlado Černý in 1985. The method is an adaptation of the Metropolis-Hastings algorithm
Metropolis-Hastings algorithm
In mathematics and physics, the Metropolis–Hastings algorithm is a Markov chain Monte Carlo method for obtaining a sequence of random samples from a probability distribution for which direct sampling is difficult...
, a Monte Carlo method
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
to generate sample states of a thermodynamic system, invented by M.N. Rosenbluth
Marshall Rosenbluth
Marshall Nicholas Rosenbluth was an American plasma physicist and member of the National Academy of Sciences. In 1997 he was awarded the National Medal of Science for discoveries in controlled thermonuclear fusion, contributions to plasma physics and work in computational statistical mechanics. ...
in a paper by N. Metropolis
Nicholas Metropolis
Nicholas Constantine Metropolis was a Greek American physicist.-Work:Metropolis received his B.Sc. and Ph.D. degrees in physics at the University of Chicago...
et al. in 1953.
Overview
In the simulated annealing (SA) method, each point s of the search space is analogous to a stateThermodynamic state
A thermodynamic state is a set of values of properties of a thermodynamic system that must be specified to reproduce the system. The individual parameters are known as state variables, state parameters or thermodynamic variables. Once a sufficient set of thermodynamic variables have been...
of some physical system
Physical system
In physics, the word system has a technical meaning, namely, it is the portion of the physical universe chosen for analysis. Everything outside the system is known as the environment, which in analysis is ignored except for its effects on the system. The cut between system and the world is a free...
, and the function E(s) to be minimized is analogous to the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of the system in that state. The goal is to bring the system, from an arbitrary initial state, to a state with the minimum possible energy.
The basic iteration
At each step, the SA heuristic considers some neighbouring state s' of the current state s, and probabilistically decides between moving the system to state s' or staying in state s. These probabilities ultimately lead the system to move to states of lower energy. Typically this step is repeated until the system reaches a state that is good enough for the application, or until a given computation budget has been exhausted.The neighbours of a state
The neighbours of a state are new states of the problem that are produced after altering the given state in some particular way. For example, in the traveling salesman problem, each state is typically defined as a particular permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of the cities to be visited. The neighbours of some particular permutation are the permutations that are produced for example by interchanging a pair of adjacent cities. The action taken to alter the solution in order to find neighbouring solutions is called "move" and different "moves" give different neighbours. These moves usually result in minimal alterations of the solution, as the previous example depicts, in order to help an algorithm to optimize the solution to the maximum extent and also to retain the already optimum parts of the solution and affect only the suboptimum parts. In the previous example, the parts of the solution are the parts of the tour.
Searching for neighbours to a state is fundamental to optimization because the final solution will come after a tour of successive neighbours. Simple heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
s move by finding best neighbour after best neighbour and stop when they have reached a solution which has no neighbours that are better solutions. The problem with this approach is that a solution that does not have any immediate neighbours that are better solutions is not necessarily the optimum. It would be the optimum if it was shown that any kind of alteration of the solution does not give a better solution and not just a particular kind of alteration. For this reason it is said that simple heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
s can only reach local optima
Local optimum
Local optimum is a term in applied mathematics and computer science.A local optimum of a combinatorial optimization problem is a solution that is optimal within a neighboring set of solutions...
and not the global optimum
Global optimum
In mathematics, a global optimum is a selection from a given domain which yields either the highest value or lowest value , when a specific function is applied. For example, for the function...
. Metaheuristics, although they also optimize through the neighbourhood approach, differ from heuristics in that they can move through neighbours that are worse solutions than the current solution. Simulated Annealing in particular doesn't even try to find the best neighbour. The reason for this is that the search can no longer stop in a local optimum and in theory, if the metaheuristic can run for an infinite amount of time, the global optimum will be found.
Acceptance probabilities
The probability of making the transition from the current state to a candidate new state
to a candidate new state 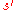 is specified by an acceptance probability function
is specified by an acceptance probability function  , that depends on the energies
, that depends on the energies 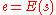 and
and  of the two states, and on a global time-varying parameter
of the two states, and on a global time-varying parameter  called the temperature.
called the temperature.States with a smaller energy are better than those with a greater energy.
The probability function
 must be positive even when
must be positive even when 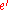 is greater than
is greater than  . This feature prevents the method from becoming stuck at a local minimum that is worse than the global one.
. This feature prevents the method from becoming stuck at a local minimum that is worse than the global one.When
 tends to zero, the probability
tends to zero, the probability 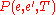 must tend to zero if
must tend to zero if  and to a positive value otherwise. For sufficiently small values of
and to a positive value otherwise. For sufficiently small values of  , the system will then increasingly favor moves that go "downhill" (i.e., to lower energy values), and avoid those that go "uphill." With
, the system will then increasingly favor moves that go "downhill" (i.e., to lower energy values), and avoid those that go "uphill." With  the procedure reduces to the greedy algorithm
the procedure reduces to the greedy algorithmGreedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
, which makes only the downhill transitions.
In the original description of SA, the probability
 was equal to 1 when
was equal to 1 when  — i.e., the procedure always moved downhill when it found a way to do so, irrespective of the temperature. Many descriptions and implementations of SA still take this condition as part of the method's definition. However, this condition is not essential for the method to work, and one may argue that it is both counterproductive and contrary to the method's principle.
— i.e., the procedure always moved downhill when it found a way to do so, irrespective of the temperature. Many descriptions and implementations of SA still take this condition as part of the method's definition. However, this condition is not essential for the method to work, and one may argue that it is both counterproductive and contrary to the method's principle.The
 function is usually chosen so that the probability of accepting a move decreases when the difference
function is usually chosen so that the probability of accepting a move decreases when the difference increases—that is, small uphill moves are more likely than large ones. However, this requirement is not strictly necessary, provided that the above requirements are met.
increases—that is, small uphill moves are more likely than large ones. However, this requirement is not strictly necessary, provided that the above requirements are met.Given these properties, the temperature
 plays a crucial role in controlling the evolution of the state
plays a crucial role in controlling the evolution of the state  of the system vis-a-vis its sensitivity to the variations of system energies. To be precise, for a large
of the system vis-a-vis its sensitivity to the variations of system energies. To be precise, for a large  , the evolution of
, the evolution of  is sensitive to coarser energy variations, while it is sensitive to finer energy variations when
is sensitive to coarser energy variations, while it is sensitive to finer energy variations when  is small.
is small.The annealing schedule
The name and inspiration of the algorithm demand an interesting feature related to the temperature variation to be embedded in the operational characteristics of the algorithm. This necessitates a gradual reduction of the temperature as the simulation proceeds. The algorithm starts initially with set to a high value (or infinity), and then it is decreased at each step following some annealing schedule—which may be specified by the user, but must end with
set to a high value (or infinity), and then it is decreased at each step following some annealing schedule—which may be specified by the user, but must end with  towards the end of the allotted time budget. In this way, the system is expected to wander initially towards a broad region of the search space containing good solutions, ignoring small features of the energy function; then drift towards low-energy regions that become narrower and narrower; and finally move downhill according to the steepest descent heuristic.
towards the end of the allotted time budget. In this way, the system is expected to wander initially towards a broad region of the search space containing good solutions, ignoring small features of the energy function; then drift towards low-energy regions that become narrower and narrower; and finally move downhill according to the steepest descent heuristic. |  |
Example illustrating the effect of cooling schedule on the performance of simulated annealing. The problem is to rearrange the pixel Pixel In digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled.... s of an image so as to minimize a certain potential energy Potential energy In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule... function, which causes similar colours to attract at short range and repel at a slightly larger distance. The elementary moves swap two adjacent pixels. These images were obtained with a fast cooling schedule (left) and a slow cooling schedule (right), producing results similar to amorphous Amorphous solid In condensed matter physics, an amorphous or non-crystalline solid is a solid that lacks the long-range order characteristic of a crystal.... and crystalline solids, respectively. | |
For any given finite problem, the probability that the simulated annealing algorithm terminates with the global optimal
Global optimum
In mathematics, a global optimum is a selection from a given domain which yields either the highest value or lowest value , when a specific function is applied. For example, for the function...
solution approaches 1 as the annealing schedule is extended. This theoretical result, however, is not particularly helpful, since the time required to ensure a significant probability of success will usually exceed the time required for a complete search
Brute-force search
In computer science, brute-force search or exhaustive search, also known as generate and test, is a trivial but very general problem-solving technique that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem's...
of the solution space.
Pseudocode
The following pseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
presents the simulated annealing heuristic as described above. It starts from a state s0 and continues to either a maximum of kmax steps or until a state with an energy of emax or less is found. In the process, the call neighbour(s) should generate a randomly chosen neighbour of a given state s; the call random should return a random value in the range
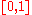 . The annealing schedule is defined by the call temp(r), which should yield the temperature to use, given the fraction r of the time budget that has been expended so far.
. The annealing schedule is defined by the call temp(r), which should yield the temperature to use, given the fraction r of the time budget that has been expended so far.
s ← s0; e ← E(s) // Initial state, energy.
sbest ← s; ebest ← e // Initial "best" solution
k ← 0 // Energy evaluation count.
while k < kmax and e > emax // While time left & not good enough:
snew ← neighbour(s) // Pick some neighbour.
enew ← E(snew) // Compute its energy.
if P(e, enew, temp(k/kmax)) > random then // Should we move to it?
s ← snew; e ← enew // Yes, change state.
if enew < ebest then // Is this a new best?
sbest ← snew; ebest ← enew // Save 'new neighbour' to 'best found'.
k ← k + 1 // One more evaluation done
return sbest // Return the best solution found.
Pedantically speaking, the "pure" SA algorithm does not keep track of the best solution found so far: it does not use the variables sbest and ebest, it lacks the second if inside the loop, and, at the end, it returns the current state s instead of sbest. While remembering the best state is a standard technique in optimization that can be used in any metaheuristic
Metaheuristic
In computer science, metaheuristic designates a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. Metaheuristics make few or no assumptions about the problem being optimized and can search very large spaces...
, it does not have an analogy with physical annealing — since a physical system can "store" a single state only.
Even more pedantically speaking, saving the best state is not necessarily an improvement, since one may have to specify a smaller kmax in order to compensate for the higher cost per iteration and since there is a good probability that sbest equals s in the final iteration anyway. However, the step sbest ← snew happens only on a small fraction of the moves. Therefore, the optimization is usually worthwhile, even when state-copying is an expensive operation.
Selecting the parameters
In order to apply the SA method to a specific problem, one must specify the following parameters: the state space, the energy (goal) function E, the candidate generator procedure neighbour, the acceptance probability function P, and the annealing schedule temp AND initial temperatureDiameter of the search graph
Simulated annealing may be modeled as a random walk on a search graphGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, whose vertices are all possible states, and whose edges are the candidate moves. An essential requirement for the neighbour function is that it must provide a sufficiently short path on this graph from the initial state to any state which may be the global optimum. (In other words, the diameter of the search graph must be small.) In the traveling salesman example above, for instance, the search space for
 cities has
cities has 
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
= 2,432,902,008,176,640,000 (2.4 quintillion) states; yet the neighbour generator function that swaps two consecutive cities can get from any state (tour) to any other state in at most
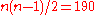 steps.
steps.Transition probabilities
For each edge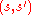 of the search graph, one defines a transition probability, which is the probability that the SA algorithm will move to state
of the search graph, one defines a transition probability, which is the probability that the SA algorithm will move to state 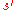 when its current state is
when its current state is  . This probability depends on the current temperature as specified by temp, by the order in which the candidate moves are generated by the neighbour function, and by the acceptance probability function P. (Note that the transition probability is not simply
. This probability depends on the current temperature as specified by temp, by the order in which the candidate moves are generated by the neighbour function, and by the acceptance probability function P. (Note that the transition probability is not simply 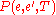 , because the candidates are tested serially.)
, because the candidates are tested serially.)Acceptance probabilities
The specification of neighbour, P, and temp is partially redundant. In practice, it's common to use the same acceptance function P for many problems, and adjust the other two functions according to the specific problem.In the formulation of the method by Kirkpatrick et al., the acceptance probability function
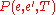 was defined as 1 if
was defined as 1 if  , and
, and  otherwise. This formula was superficially justified by analogy with the transitions of a physical system; it corresponds to the Metropolis-Hastings algorithm
otherwise. This formula was superficially justified by analogy with the transitions of a physical system; it corresponds to the Metropolis-Hastings algorithmMetropolis-Hastings algorithm
In mathematics and physics, the Metropolis–Hastings algorithm is a Markov chain Monte Carlo method for obtaining a sequence of random samples from a probability distribution for which direct sampling is difficult...
, in the case where the proposal distribution of Metropolis-Hastings is symmetric. However, this acceptance probability is often used for simulated annealing even when the neighbour function, which is analogous to the proposal distribution in Metropolis-Hastings, is not symmetric, or not probabilistic at all. As a result, the transition probabilities of the simulated annealing algorithm do not correspond to the transitions of the analogous physical system, and the long-term distribution of states at a constant temperature
 need not bear any resemblance to the thermodynamic equilibrium distribution over states of that physical system, at any temperature. Nevertheless, most descriptions of SA assume the original acceptance function, which is probably hard-coded in many implementations of SA.
need not bear any resemblance to the thermodynamic equilibrium distribution over states of that physical system, at any temperature. Nevertheless, most descriptions of SA assume the original acceptance function, which is probably hard-coded in many implementations of SA.Efficient candidate generation
When choosing the candidate generator neighbour, one must consider that after a few iterations of the SA algorithm, the current state is expected to have much lower energy than a random state. Therefore, as a general rule, one should skew the generator towards candidate moves where the energy of the destination state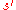 is likely to be similar to that of the current state. This heuristic
is likely to be similar to that of the current state. This heuristicHeuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
(which is the main principle of the Metropolis-Hastings algorithm
Metropolis-Hastings algorithm
In mathematics and physics, the Metropolis–Hastings algorithm is a Markov chain Monte Carlo method for obtaining a sequence of random samples from a probability distribution for which direct sampling is difficult...
) tends to exclude "very good" candidate moves as well as "very bad" ones; however, the latter are usually much more common than the former, so the heuristic is generally quite effective.
In the traveling salesman problem above, for example, swapping two consecutive cities in a low-energy tour is expected to have a modest effect on its energy (length); whereas swapping two arbitrary cities is far more likely to increase its length than to decrease it. Thus, the consecutive-swap neighbour generator is expected to perform better than the arbitrary-swap one, even though the latter could provide a somewhat shorter path to the optimum (with
 swaps, instead of
swaps, instead of 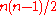 ).
).A more precise statement of the heuristic is that one should try first candidate states
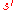 for which
for which 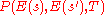 is large. For the "standard" acceptance function
is large. For the "standard" acceptance function  above, it means that
above, it means that  is on the order of
is on the order of  or less. Thus, in the traveling salesman example above, one could use a neighbour function that swaps two random cities, where the probability of choosing a city pair vanishes as their distance increases beyond
or less. Thus, in the traveling salesman example above, one could use a neighbour function that swaps two random cities, where the probability of choosing a city pair vanishes as their distance increases beyond  .
.Barrier avoidance
When choosing the candidate generator neighbour one must also try to reduce the number of "deep" local minima — states (or sets of connected states) that have much lower energy than all its neighbouring states. Such "closed catchmentDrainage basin
A drainage basin is an extent or an area of land where surface water from rain and melting snow or ice converges to a single point, usually the exit of the basin, where the waters join another waterbody, such as a river, lake, reservoir, estuary, wetland, sea, or ocean...
basins" of the energy function may trap the SA algorithm with high probability (roughly proportional to the number of states in the basin) and for a very long time (roughly exponential on the energy difference between the surrounding states and the bottom of the basin).
As a rule, it is impossible to design a candidate generator that will satisfy this goal and also prioritize candidates with similar energy. On the other hand, one can often vastly improve the efficiency of SA by relatively simple changes to the generator. In the traveling salesman problem, for instance, it is not hard to exhibit two tours
 ,
,  , with nearly equal lengths, such that (0)
, with nearly equal lengths, such that (0)  is optimal, (1) every sequence of city-pair swaps that converts
is optimal, (1) every sequence of city-pair swaps that converts  to
to  goes through tours that are much longer than both, and (2)
goes through tours that are much longer than both, and (2)  can be transformed into
can be transformed into  by flipping (reversing the order of) a set of consecutive cities. In this example,
by flipping (reversing the order of) a set of consecutive cities. In this example,  and
and  lie in different "deep basins" if the generator performs only random pair-swaps; but they will be in the same basin if the generator performs random segment-flips.
lie in different "deep basins" if the generator performs only random pair-swaps; but they will be in the same basin if the generator performs random segment-flips.Cooling schedule
The physical analogy that is used to justify SA assumes that the cooling rate is low enough for the probability distribution of the current state to be near thermodynamic equilibriumThermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
at all times. Unfortunately, the relaxation time—the time one must wait for the equilibrium to be restored after a change in temperature—strongly depends on the "topography" of the energy function and on the current temperature. In the SA algorithm, the relaxation time also depends on the candidate generator, in a very complicated way. Note that all these parameters are usually provided as black box functions
Procedural parameter
In computing, a procedural parameter is a parameter of a procedure that is itself a procedure.This concept is an extremely powerful and versatile programming tool, because it allows programmers to modify certain steps of a library procedure in arbitrarily complicated ways, without having to...
to the SA algorithm.
Therefore, in practice the ideal cooling rate cannot be determined beforehand, and should be empirically adjusted for each problem. The variant of SA known as thermodynamic simulated annealing tries to avoid this problem by dispensing with the cooling schedule, and instead automatically adjusting the temperature at each step based on the energy difference between the two states, according to the laws of thermodynamics.
Restarts
Sometimes it is better to move back to a solution that was significantly better rather than always moving from the current state. This process is called restarting of simulated annealing. To do this we sets and e to sbest and ebest and perhaps restart the annealing schedule. The decision to restart could be based on several criteria. notable among these include restarting based a fixed number of steps, based on whether the current energy being too high from the best energy obtained so far, restarting randomly etc.Related methods
- Quantum annealingQuantum annealingIn mathematics and applications, quantum annealing is a general method for finding the global minimum of a given objective function over a given set of candidate solutions , by a process analogous to quantum fluctuations...
uses "quantum fluctuations" instead of thermal fluctuations to get through high but thin barriers in the target function.
- Stochastic tunnelingStochastic tunnelingStochastic tunneling is an approach to global optimization based on the Monte Carlo method-sampling of the function to be minimized.- Idea :...
attempts to overcome the increasing difficulty simulated annealing runs have in escaping from local minima as the temperature decreases, by 'tunneling' through barriers.
- Tabu searchTabu searchTabu search is a mathematical optimization method, belonging to the class of trajectory based techniques. Tabu search enhances the performance of a local search method by using memory structures that describe the visited solutions: once a potential solution has been determined, it is marked as...
normally moves to neighbouring states of lower energy, but will take uphill moves when it finds itself stuck in a local minimum; and avoids cycles by keeping a "taboo list" of solutions already seen.
- Reactive search optimizationReactive search optimizationReactive search optimization defines local-search heuristics based on machine learning, a family of optimization algorithms based on the local search techniques...
focuses on combining machine learning with optimization, by adding an internal feedback loop to self-tune the free parameters of an algorithm to the characteristics of the problem, of the instance, and of the local situation around the current solution.
- Stochastic gradient descentStochastic gradient descentStochastic gradient descent is an optimization method for minimizing an objective function that is written as a sum of differentiable functions.- Background :...
runs many greedy searches from random initial locations.
- Genetic algorithms maintain a pool of solutions rather than just one. New candidate solutions are generated not only by "mutation" (as in SA), but also by "recombination" of two solutions from the pool. Probabilistic criteria, similar to those used in SA, are used to select the candidates for mutation or combination, and for discarding excess solutions from the pool.
- Graduated optimizationGraduated optimizationGraduated optimization is a global optimization technique that attempts to solve a difficult optimization problem by initially solving a greatly simplified problem, and progressively transforming that problem until it is equivalent to the difficult optimization problem.-Technique...
digressively "smooths" the target function while optimizing.
- Ant colony optimizationAnt colony optimizationIn computer science and operations research, the ant colony optimization algorithm ' is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs....
(ACO) uses many ants (or agents) to traverse the solution space and find locally productive areas.
- The cross-entropy methodCross-entropy methodThe cross-entropy method attributed to Reuven Rubinstein is a general Monte Carlo approach tocombinatorial and continuous multi-extremal optimization and importance sampling.The method originated from the field of rare event simulation, where...
(CE) generates candidates solutions via a parameterized probability distribution. The parameters are updated via cross-entropy minimization, so as to generate better samples in the next iteration.
- Harmony searchHarmony searchIn computer science and operations research, harmony search is a phenomenon-mimicking algorithm inspired by the improvisation process of musicians...
mimics musicians in improvisation process where each musician plays a note for finding a best harmony all together.
- Stochastic optimizationStochastic optimizationStochastic optimization methods are optimization methods that generate and use random variables. For stochastic problems, the random variables appear in the formulation of the optimization problem itself, which involve random objective functions or random constraints, for example. Stochastic...
is an umbrella set of methods that includes simulated annealing and numerous other approaches.
- Particle swarm optimizationParticle swarm optimizationIn computer science, particle swarm optimization is a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality...
is an algorithm modelled on swarm intelligence that finds a solution to an optimization problem in a search space, or model and predict social behavior in the presence of objectives.
- Intelligent Water Drops (IWD) which mimics the behavior of natural water drops to solve optimization problems
- Parallel temperingParallel temperingParallel tempering, also known as replica exchange MCMC sampling, is a simulation method aimed at improving the dynamic properties of Monte Carlo method simulations of physical systems, and of Markov chain Monte Carlo sampling methods more generally...
is a simulation of model copies at different temperatures (or HamiltonianHamiltonianHamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...
s) to overcome the potential barriers.
See also
Further reading
- A. Das and B. K. Chakrabarti (Eds.), Quantum Annealing and Related Optimization Methods, Lecture Note in Physics, Vol. 679, Springer, Heidelberg (2005)}}
External links
- Simulated Annealing visualization A visualization of a simulated annealing solution to the N-Queens puzzle by Yuval Baror.
- Global optimization algorithms for MATLAB
- Simulated Annealing A Java applet that allows you to experiment with simulated annealing. Source code included.
- "General Simulated Annealing Algorithm" An open-source MATLAB program for general simulated annealing exercises.
- Self-Guided Lesson on Simulated Annealing A Wikiversity project.
- Google in superposition of using, not using quantum computer Ars Technica discusses the possibility that the D-Wave computer being used by google may, in fact, be an efficient SA co-processor
- Minimizing Multimodal Functions of Continuous Variables with Simulated Annealing A Fortran 77 simulated annealing code.

