
Continuum hypothesis
Encyclopedia
In mathematics
, the continuum hypothesis (abbreviated CH) is a hypothesis
, advanced by Georg Cantor
in 1874, about the possible sizes of infinite sets. It states:
Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems
presented in the year 1900. The contributions of Kurt Gödel
in 1940 and Paul Cohen
in 1963 showed that the hypothesis can neither be disproved nor be proved
using the axioms of Zermelo-Fraenkel set theory, the standard foundation of modern mathematics, provided ZF set theory is consistent
.
The name of the hypothesis comes from the term the continuum for the real numbers.
if there exists a bijection
(a one-to-one correspondence) between them. Intuitively, for two sets S and T to have the same cardinality means that it is possible to "pair off" elements of S with elements of T in such a fashion that every element of S is paired off with exactly one element of T and vice versa. Hence, the set {banana, apple, pear} has the same cardinality as {yellow, red, green}.
With infinite sets such as the set of integer
s or rational number
s, this becomes more complicated to demonstrate. The rational numbers seemingly form a counterexample to the continuum hypothesis: the integers form a proper subset of the rationals, a proper subset of the reals, so intuitively, there are more rational numbers than integers, and fewer rational numbers than real numbers. However, this intuitive analysis does not take account of the fact that all three sets are infinite. It turns out the rational numbers can actually be placed in one-to-one correspondence with the integers, and therefore the set of rational numbers is the same size (cardinality) as the set of integers: they are both countable set
s.
Cantor gave two proofs that the cardinality of the set of integer
s is strictly smaller than that of the set of real number
s (see Cantor's first uncountability proof
and Cantor's diagonal argument
). His proofs, however, give no indication of the extent to which the cardinality of the integers is less than that of the real numbers. Cantor proposed the continuum hypothesis as a possible solution to this question.
The hypothesis states that the set of real numbers has minimal possible cardinality which is greater than the cardinality of the set of integers. Equivalently, as the cardinality
of the integers is ("aleph-naught") and the cardinality of the real numbers is
("aleph-naught") and the cardinality of the real numbers is 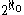 , the continuum hypothesis says that there is no set
, the continuum hypothesis says that there is no set  for which
for which
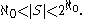
Assuming the axiom of choice, there is a smallest cardinal number greater than
greater than 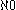 , and the continuum hypothesis is in turn equivalent to the equality
, and the continuum hypothesis is in turn equivalent to the equality
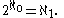
There is also a generalization of the continuum hypothesis called the generalized continuum hypothesis (GCH) which says that for all ordinals
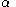
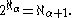
A consequence of the hypothesis is that every infinite subset
of the real numbers either has the same cardinality as the integers or the same cardinality as the entire set of the reals.
it, in vain. It became the first on David Hilbert's list of important open questions
that was presented at the International Congress of Mathematicians
in the year 1900 in Paris. Axiomatic set theory was at that point not yet formulated.
Kurt Gödel
showed in 1940 that the continuum hypothesis (CH for short) cannot be disproved from the standard Zermelo-Fraenkel set theory (ZF), even if the axiom of choice is adopted (ZFC). Paul Cohen
showed in 1963 that CH cannot be proven from those same axioms either. Hence, CH is independent
of ZFC. Both of these results assume that the Zermelo-Fraenkel axioms themselves do not contain a contradiction; this assumption is widely believed to be true.
The continuum hypothesis was not the first statement shown to be independent of ZFC. An immediate consequence of Gödel's incompleteness theorem, which was published in 1931, is that there is a formal statement expressing the consistency of ZFC that is independent of ZFC. This consistency statement is of a metamathematical, rather than purely mathematical, character. The continuum hypothesis and the axiom of choice were among the first mathematical statements shown to be independent of ZF set theory. These independence proofs were not completed until Paul Cohen developed forcing
in the 1960s.
The continuum hypothesis is closely related to many statements in analysis
, point set topology
and measure theory. As a result of its independence, many substantial conjecture
s in those fields have subsequently been shown to be independent as well.
So far, CH appears to be independent of all known large cardinal axioms in the context of ZFC.
Gödel and Cohen's negative results are not universally accepted as disposing of the hypothesis, and Hilbert's problem remains an active topic of contemporary research (see Woodin 2001a).
Historically, mathematicians who favored a "rich" and "large" universe
of sets were against CH, while those favoring a "neat" and "controllable" universe favored CH. Parallel arguments were made for and against the axiom of constructibility
, which implies CH. More recently, Matthew Foreman
has pointed out that ontological maximalism
can actually be used to argue in favor of CH, because among models that have the same reals, models with "more" sets of reals have a better chance of satisfying CH (Maddy 1988, p. 500).
Another viewpoint is that the conception of set is not specific enough to determine whether CH is true or false. This viewpoint was advanced as early as 1923 by Skolem, even before Gödel's first incompleteness theorem. Skolem argued on the basis of what is now known as Skolem's paradox
, and it was later supported by the independence of CH from the axioms of ZFC, since these axioms are enough to establish the elementary properties of sets and cardinalities. In order to argue against this viewpoint, it would be sufficient to demonstrate new axioms that are supported by intuition and resolve CH in one direction or another. Although the axiom of constructibility
does resolve CH, it is not generally considered to be intuitively true any more than CH is generally considered to be false (Kunen 1980, p. 171).
At least two other axioms have been proposed that have implications for the continuum hypothesis, although these axioms have not currently found wide acceptance in the mathematical community. In 1986, Chris Freiling presented an argument against CH by showing that the negation of CH is equivalent to Freiling's axiom of symmetry
, a statement about probabilities
. Freiling believes this axiom is "intuitively true" but others have disagreed. A difficult argument against CH developed by W. Hugh Woodin
has attracted considerable attention since the year 2000 (Woodin 2001a, 2001b). Foreman (2003) does not reject Woodin's argument outright but urges caution.
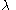 there is no cardinal
there is no cardinal 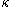 such that
such that 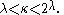 An equivalent condition is that
An equivalent condition is that 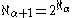 for every ordinal
for every ordinal
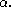 The beth number
The beth number
s provide an alternate notation for this condition: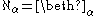 for every ordinal
for every ordinal 
This is a generalization of the continuum hypothesis since the continuum has the same cardinality as the power set of the integers. Like CH, GCH is also independent of ZFC, but Sierpiński proved that ZF + GCH implies the axiom of choice (AC), so choice and GCH are not independent in ZF; there are no models of ZF in which GCH holds and AC fails.
Kurt Gödel
showed that GCH is a consequence of ZF + V=L
(the axiom that every set is constructible relative to the ordinals), and is consistent with ZFC. As GCH implies CH, Cohen's model in which CH fails is a model in which GCH fails, and thus GCH is not provable from ZFC. W. B. Easton used the method of forcing developed by Cohen to prove Easton's theorem
, which shows it is consistent with ZFC for arbitrarily large cardinals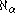 to fail to satisfy
to fail to satisfy 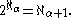 Much later, Foreman
Much later, Foreman
and Woodin
proved that (assuming the consistency of very large cardinals) it is consistent that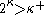 holds for every infinite cardinal
holds for every infinite cardinal 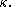 Later Woodin extended this by showing the consistency of
Later Woodin extended this by showing the consistency of  for every
for every  . A recent result of Carmi Merimovich shows that, for each n≥1, it is consistent with ZFC that for each κ, 2κ is the nth successor of κ. On the other hand, Laszlo Patai proved, that if γ is an ordinal and for each infinite cardinal κ, 2κ is the γth successor of κ, then γ is finite.
. A recent result of Carmi Merimovich shows that, for each n≥1, it is consistent with ZFC that for each κ, 2κ is the nth successor of κ. On the other hand, Laszlo Patai proved, that if γ is an ordinal and for each infinite cardinal κ, 2κ is the γth successor of κ, then γ is finite.
For any infinite sets A and B, if there is an injection from A to B then there is an injection from subsets of A to subsets of B. Thus for any infinite cardinals A and B,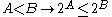 .
.
If A and B are finite, the stronger inequality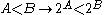
holds. GCH implies that this strict, stronger inequality holds for infinite cardinals as well as finite cardinals.
 is:
is: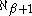 when α ≤ β+1;
when α ≤ β+1; when β+1 < α and
when β+1 < α and 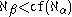 where cf is the cofinality
where cf is the cofinality
operation; and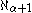 when β+1 < α and
when β+1 < α and 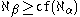 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the continuum hypothesis (abbreviated CH) is a hypothesis
Hypothesis
A hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...
, advanced by Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
in 1874, about the possible sizes of infinite sets. It states:
- There is no set whose cardinality is strictly between that of the integers and that of the real numbers.
Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems
Hilbert's problems
Hilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
presented in the year 1900. The contributions of Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
in 1940 and Paul Cohen
Paul Cohen (mathematician)
Paul Joseph Cohen was an American mathematician best known for his proof of the independence of the continuum hypothesis and the axiom of choice from Zermelo–Fraenkel set theory, the most widely accepted axiomatization of set theory.-Early years:Cohen was born in Long Branch, New Jersey, into a...
in 1963 showed that the hypothesis can neither be disproved nor be proved
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
using the axioms of Zermelo-Fraenkel set theory, the standard foundation of modern mathematics, provided ZF set theory is consistent
Consistency
Consistency can refer to:* Consistency , the psychological need to be consistent with prior acts and statements* "Consistency", an 1887 speech by Mark Twain...
.
The name of the hypothesis comes from the term the continuum for the real numbers.
Cardinality of infinite sets
Two sets are said to have the same cardinality or cardinal numberCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
if there exists a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
(a one-to-one correspondence) between them. Intuitively, for two sets S and T to have the same cardinality means that it is possible to "pair off" elements of S with elements of T in such a fashion that every element of S is paired off with exactly one element of T and vice versa. Hence, the set {banana, apple, pear} has the same cardinality as {yellow, red, green}.
With infinite sets such as the set of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s or rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, this becomes more complicated to demonstrate. The rational numbers seemingly form a counterexample to the continuum hypothesis: the integers form a proper subset of the rationals, a proper subset of the reals, so intuitively, there are more rational numbers than integers, and fewer rational numbers than real numbers. However, this intuitive analysis does not take account of the fact that all three sets are infinite. It turns out the rational numbers can actually be placed in one-to-one correspondence with the integers, and therefore the set of rational numbers is the same size (cardinality) as the set of integers: they are both countable set
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
s.
Cantor gave two proofs that the cardinality of the set of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s is strictly smaller than that of the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s (see Cantor's first uncountability proof
Cantor's first uncountability proof
Georg Cantor's first uncountability proof demonstrates that the set of all real numbers is uncountable. This proof differs from the more familiar proof that uses his diagonal argument...
and Cantor's diagonal argument
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
). His proofs, however, give no indication of the extent to which the cardinality of the integers is less than that of the real numbers. Cantor proposed the continuum hypothesis as a possible solution to this question.
The hypothesis states that the set of real numbers has minimal possible cardinality which is greater than the cardinality of the set of integers. Equivalently, as the cardinality
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
of the integers is
 ("aleph-naught") and the cardinality of the real numbers is
("aleph-naught") and the cardinality of the real numbers is 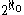 , the continuum hypothesis says that there is no set
, the continuum hypothesis says that there is no set  for which
for which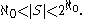
Assuming the axiom of choice, there is a smallest cardinal number
 greater than
greater than 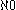 , and the continuum hypothesis is in turn equivalent to the equality
, and the continuum hypothesis is in turn equivalent to the equality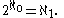
There is also a generalization of the continuum hypothesis called the generalized continuum hypothesis (GCH) which says that for all ordinals
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
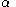
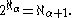
A consequence of the hypothesis is that every infinite subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the real numbers either has the same cardinality as the integers or the same cardinality as the entire set of the reals.
Impossibility of proof and disproof in ZFC
Cantor believed the continuum hypothesis to be true and tried for many years to proveMathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
it, in vain. It became the first on David Hilbert's list of important open questions
Hilbert's problems
Hilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
that was presented at the International Congress of Mathematicians
International Congress of Mathematicians
The International Congress of Mathematicians is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union ....
in the year 1900 in Paris. Axiomatic set theory was at that point not yet formulated.
Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
showed in 1940 that the continuum hypothesis (CH for short) cannot be disproved from the standard Zermelo-Fraenkel set theory (ZF), even if the axiom of choice is adopted (ZFC). Paul Cohen
Paul Cohen (mathematician)
Paul Joseph Cohen was an American mathematician best known for his proof of the independence of the continuum hypothesis and the axiom of choice from Zermelo–Fraenkel set theory, the most widely accepted axiomatization of set theory.-Early years:Cohen was born in Long Branch, New Jersey, into a...
showed in 1963 that CH cannot be proven from those same axioms either. Hence, CH is independent
Independence (mathematical logic)
In mathematical logic, independence refers to the unprovability of a sentence from other sentences.A sentence σ is independent of a given first-order theory T if T neither proves nor refutes σ; that is, it is impossible to prove σ from T, and it is also impossible to prove from T that...
of ZFC. Both of these results assume that the Zermelo-Fraenkel axioms themselves do not contain a contradiction; this assumption is widely believed to be true.
The continuum hypothesis was not the first statement shown to be independent of ZFC. An immediate consequence of Gödel's incompleteness theorem, which was published in 1931, is that there is a formal statement expressing the consistency of ZFC that is independent of ZFC. This consistency statement is of a metamathematical, rather than purely mathematical, character. The continuum hypothesis and the axiom of choice were among the first mathematical statements shown to be independent of ZF set theory. These independence proofs were not completed until Paul Cohen developed forcing
Forcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
in the 1960s.
The continuum hypothesis is closely related to many statements in analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, point set topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and measure theory. As a result of its independence, many substantial conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
s in those fields have subsequently been shown to be independent as well.
So far, CH appears to be independent of all known large cardinal axioms in the context of ZFC.
Gödel and Cohen's negative results are not universally accepted as disposing of the hypothesis, and Hilbert's problem remains an active topic of contemporary research (see Woodin 2001a).
Arguments for and against CH
Gödel believed that CH is false and that his proof that CH is consistent only shows that the Zermelo-Fraenkel axioms do not adequately describe the universe of sets. Gödel was a platonist and therefore had no problems with asserting the truth and falsehood of statements independent of their provability. Cohen, though a formalist, also tended towards rejecting CH.Historically, mathematicians who favored a "rich" and "large" universe
Universe (mathematics)
In mathematics, and particularly in set theory and the foundations of mathematics, a universe is a class that contains all the entities one wishes to consider in a given situation...
of sets were against CH, while those favoring a "neat" and "controllable" universe favored CH. Parallel arguments were made for and against the axiom of constructibility
Axiom of constructibility
The axiom of constructibility is a possible axiom for set theory in mathematics that asserts that every set is constructible. The axiom is usually written as V = L, where V and L denote the von Neumann universe and the constructible universe, respectively.- Implications :The axiom of...
, which implies CH. More recently, Matthew Foreman
Matthew Foreman
Matthew Dean Foreman is a set theorist at University of California, Irvine. He has made contributions in widely varying areas of set theory, including descriptive set theory, forcing, and infinitary combinatorics....
has pointed out that ontological maximalism
Ontological maximalism
In philosophy, ontological maximalism is a preference for largest possible universe, i.e. anything which could exist does exist.- See also :*Ontology*Maximalism*Large cardinal property*Continuum hypothesis...
can actually be used to argue in favor of CH, because among models that have the same reals, models with "more" sets of reals have a better chance of satisfying CH (Maddy 1988, p. 500).
Another viewpoint is that the conception of set is not specific enough to determine whether CH is true or false. This viewpoint was advanced as early as 1923 by Skolem, even before Gödel's first incompleteness theorem. Skolem argued on the basis of what is now known as Skolem's paradox
Skolem's paradox
In mathematical logic and philosophy, Skolem's paradox is a seeming contradiction that arises from the downward Löwenheim–Skolem theorem. Thoralf Skolem was the first to discuss the seemingly contradictory aspects of the theorem, and to discover the relativity of set-theoretic notions now known as...
, and it was later supported by the independence of CH from the axioms of ZFC, since these axioms are enough to establish the elementary properties of sets and cardinalities. In order to argue against this viewpoint, it would be sufficient to demonstrate new axioms that are supported by intuition and resolve CH in one direction or another. Although the axiom of constructibility
Axiom of constructibility
The axiom of constructibility is a possible axiom for set theory in mathematics that asserts that every set is constructible. The axiom is usually written as V = L, where V and L denote the von Neumann universe and the constructible universe, respectively.- Implications :The axiom of...
does resolve CH, it is not generally considered to be intuitively true any more than CH is generally considered to be false (Kunen 1980, p. 171).
At least two other axioms have been proposed that have implications for the continuum hypothesis, although these axioms have not currently found wide acceptance in the mathematical community. In 1986, Chris Freiling presented an argument against CH by showing that the negation of CH is equivalent to Freiling's axiom of symmetry
Freiling's axiom of symmetry
Freiling's axiom of symmetry is a set-theoretic axiom proposed by Chris Freiling. It is based on intuition of Stuart Davidsonbut the mathematics behind it goes back to Wacław Sierpiński....
, a statement about probabilities
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
. Freiling believes this axiom is "intuitively true" but others have disagreed. A difficult argument against CH developed by W. Hugh Woodin
W. Hugh Woodin
William Hugh Woodin is an American mathematician and set theorist at University of California, Berkeley. He has made many notable contributions to the theory of inner models and determinacy. A type of large cardinal, the Woodin cardinal, bears his name.-Biography:Born in Tucson, Arizona, Woodin...
has attracted considerable attention since the year 2000 (Woodin 2001a, 2001b). Foreman (2003) does not reject Woodin's argument outright but urges caution.
The generalized continuum hypothesis
The generalized continuum hypothesis (GCH) states that if an infinite set's cardinality lies between that of an infinite set S and that of the power set of S, then it either has the same cardinality as the set S or the same cardinality as the power set of S. That is, for any infinite cardinalCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
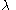 there is no cardinal
there is no cardinal 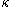 such that
such that 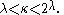 An equivalent condition is that
An equivalent condition is that 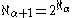 for every ordinal
for every ordinalOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
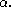 The beth number
The beth numberBeth number
In mathematics, the infinite cardinal numbers are represented by the Hebrew letter \aleph indexed with a subscript that runs over the ordinal numbers...
s provide an alternate notation for this condition:
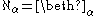 for every ordinal
for every ordinal 
This is a generalization of the continuum hypothesis since the continuum has the same cardinality as the power set of the integers. Like CH, GCH is also independent of ZFC, but Sierpiński proved that ZF + GCH implies the axiom of choice (AC), so choice and GCH are not independent in ZF; there are no models of ZF in which GCH holds and AC fails.
Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
showed that GCH is a consequence of ZF + V=L
Axiom of constructibility
The axiom of constructibility is a possible axiom for set theory in mathematics that asserts that every set is constructible. The axiom is usually written as V = L, where V and L denote the von Neumann universe and the constructible universe, respectively.- Implications :The axiom of...
(the axiom that every set is constructible relative to the ordinals), and is consistent with ZFC. As GCH implies CH, Cohen's model in which CH fails is a model in which GCH fails, and thus GCH is not provable from ZFC. W. B. Easton used the method of forcing developed by Cohen to prove Easton's theorem
Easton's theorem
In set theory, Easton's theorem is a result on the possible cardinal numbers of powersets. showed via forcing that...
, which shows it is consistent with ZFC for arbitrarily large cardinals
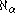 to fail to satisfy
to fail to satisfy 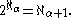 Much later, Foreman
Much later, ForemanMatthew Foreman
Matthew Dean Foreman is a set theorist at University of California, Irvine. He has made contributions in widely varying areas of set theory, including descriptive set theory, forcing, and infinitary combinatorics....
and Woodin
W. Hugh Woodin
William Hugh Woodin is an American mathematician and set theorist at University of California, Berkeley. He has made many notable contributions to the theory of inner models and determinacy. A type of large cardinal, the Woodin cardinal, bears his name.-Biography:Born in Tucson, Arizona, Woodin...
proved that (assuming the consistency of very large cardinals) it is consistent that
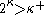 holds for every infinite cardinal
holds for every infinite cardinal 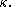 Later Woodin extended this by showing the consistency of
Later Woodin extended this by showing the consistency of  for every
for every  . A recent result of Carmi Merimovich shows that, for each n≥1, it is consistent with ZFC that for each κ, 2κ is the nth successor of κ. On the other hand, Laszlo Patai proved, that if γ is an ordinal and for each infinite cardinal κ, 2κ is the γth successor of κ, then γ is finite.
. A recent result of Carmi Merimovich shows that, for each n≥1, it is consistent with ZFC that for each κ, 2κ is the nth successor of κ. On the other hand, Laszlo Patai proved, that if γ is an ordinal and for each infinite cardinal κ, 2κ is the γth successor of κ, then γ is finite. For any infinite sets A and B, if there is an injection from A to B then there is an injection from subsets of A to subsets of B. Thus for any infinite cardinals A and B,
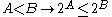 .
.If A and B are finite, the stronger inequality
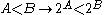
holds. GCH implies that this strict, stronger inequality holds for infinite cardinals as well as finite cardinals.
Implications of GCH for cardinal exponentiation
Although the Generalized Continuum Hypothesis refers directly only to cardinal exponentiation with 2 as the base, one can deduce from it the values of cardinal exponentiation in all cases. It implies that is:
is: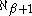 when α ≤ β+1;
when α ≤ β+1; when β+1 < α and
when β+1 < α and 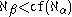 where cf is the cofinality
where cf is the cofinalityCofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
operation; and
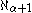 when β+1 < α and
when β+1 < α and 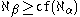 .
.

