
Aryabhata
Encyclopedia
Aryabhata (476–550 CE) was the first in the line of great mathematician
-astronomer
s from the classical age of Indian mathematics
and Indian astronomy. His most famous works are the Āryabhaṭīya
(499 CE, when he was 23 years old) and the Arya-siddhanta
.
's references to him "in more than a hundred places by name". Furthermore, in most instances "Aryabhatta" does not fit the metre either.
, when he was 23 years old. This corresponds to 499 CE, and implies that he was born in 476 CE.
Aryabhata provides no information about his place of birth. The only information comes from Bhāskara I
, who describes Aryabhata as āśmakīya, "one belonging to the aśmaka country." The Asmaka were one of the 16 of Ancient Indian Mahajanapadas
, and the only one situated south of the Vindhyas.
It is widely attested that during the mid-first millennium BCE, a branch of the Aśmaka people settled in the region between the Narmada
and Godavari rivers in central India, and it is possible Aryabhata was born there. However, early Buddhist texts describe Ashmaka as being further south, in dakshinapath or the Deccan, while other texts describe the Ashmakas as having fought Alexander.
Many are of the view that he was born in the south of India in Kerala
and lived in Magadha
at the time of the Gupta rulers.
(CE 629), identify Kusumapura as Pāṭaliputra, modern Patna
. A verse mentions that Aryabhata was the head of an institution () at Kusumapura, and, because the university of Nalanda
was in Pataliputra at the time and had an astronomical observatory, it is speculated that Aryabhata might have been the head of the Nalanda university as well. Aryabhata is also reputed to have set up an observatory at the Sun temple in Taregana
, Bihar.
in Kerala
region. For instance, one hypothesis was that aśmaka (Sanskrit for "stone") may be the region in Kerala that is now known as Koṭuṅṅallūr, based on the belief that it was earlier known as Koṭum-Kal-l-ūr ("city of hard stones"); however, old records show that the city was actually Koṭum-kol-ūr ("city of strict governance"). Similarly, the fact that several commentaries on the Aryabhatiya have come from Kerala were used to suggest that it was Aryabhata's main place of life and activity; however, many commentaries have come from outside Kerala, and the Aryasiddhanta was completely unknown in Kerala.
Aryabhata mentions "Lanka" on several occasions in the Aryabhatiya, but his "Lanka" is an abstraction, standing for a point on the equator at the same longitude as his Ujjayini.
and astronomy
, some of which are lost.
His major work, Aryabhatiya, a compendium of mathematics and astronomy, was extensively referred to in the Indian mathematical literature and has survived to modern times. The mathematical part of the Aryabhatiya covers arithmetic
, algebra
, plane trigonometry
, and spherical trigonometry
. It also contains continued fractions
, quadratic equation
s, sums-of-power series, and a table of sines
.
The Arya-siddhanta, a lost work on astronomical computations, is known through the writings of Aryabhata's contemporary, Varahamihira
, and later mathematicians and commentators, including Brahmagupta
and Bhaskara I
. This work appears to be based on the older Surya Siddhanta
and uses the midnight-day reckoning, as opposed to sunrise in Aryabhatiya. It also contained a description of several astronomical instruments: the gnomon
(shanku-yantra), a shadow instrument (chhAyA-yantra), possibly angle-measuring devices, semicircular and circular (dhanur-yantra / chakra-yantra), a cylindrical stick yasti-yantra, an umbrella-shaped device called the chhatra-yantra, and water clock
s of at least two types, bow-shaped and cylindrical.
A third text, which may have survived in the Arabic
translation, is Al ntf or Al-nanf. It claims that it is a translation by Aryabhata, but the Sanskrit name of this work is not known.
Probably dating from the 9th century, it is mentioned by the Persian
scholar and chronicler of India, Abū Rayhān al-Bīrūnī.
. The name "Aryabhatiya" is due to later commentators. Aryabhata himself may not have given it a name. His disciple Bhaskara I
calls it Ashmakatantra (or the treatise from the Ashmaka). It is also occasionally referred to as Arya-shatas-aShTa (literally, Aryabhata's 108), because there are 108 verses in the text. It is written in the very terse style typical of sutra
literature, in which each line is an aid to memory for a complex system. Thus, the explication of meaning is due to commentators. The text consists of the 108 verses and 13 introductory verses, and is divided into four pādas or chapters:
The Aryabhatiya presented a number of innovations in mathematics and astronomy in verse form, which were influential for many centuries. The extreme brevity of the text was elaborated in commentaries by his disciple Bhaskara I (Bhashya, c. 600 CE) and by Nilakantha Somayaji
in his Aryabhatiya Bhasya, (1465 CE).
, was clearly in place in his work. While he did not use a symbol for zero, the French mathematician Georges Ifrah
explains that knowledge of zero was implicit in Aryabhata's place-value system as a place holder for the powers of ten with null
coefficients
However, Aryabhata did not use the Brahmi numerals. Continuing the Sanskrit
ic tradition from Vedic times
, he used letters of the alphabet to denote numbers, expressing quantities, such as the table of sines in a mnemonic
form.
( ), and may have come to the conclusion that
), and may have come to the conclusion that  is irrational. In the second part of the Aryabhatiyam ( 10), he writes:
is irrational. In the second part of the Aryabhatiyam ( 10), he writes:
This implies that the ratio of the circumference to the diameter is ((4 + 100) × 8 + 62000)/20000 = 62832/20000 = 3.1416, which is accurate to five significant figures
.
It is speculated that Aryabhata used the word āsanna (approaching), to mean that not only is this an approximation but that the value is incommensurable (or irrational). If this is correct, it is quite a sophisticated insight, because the irrationality of pi was proved in Europe only in 1761 by Lambert
.
After Aryabhatiya was translated into Arabic
(c. 820 CE)
this approximation was mentioned in Al-Khwarizmi's book on algebra.
that translates to: "for a triangle, the result of a perpendicular with the half-side is the area."
Aryabhata discussed the concept of sine in his work by the name of ardha-jya. Literally, it means "half-chord". For simplicity, people started calling it jya. When Arabic writers translated his works from Sanskrit
into Arabic, they referred it as jiba. However, in Arabic writings, vowels are omitted, and it was abbreviated as jb. Later writers substituted it with jaib, meaning "pocket" or "fold (in a garment)". (In Arabic, jiba is a meaningless word.) Later in the 12th century, when Gherardo of Cremona translated these writings from Arabic into Latin, he replaced the Arabic jaib with its Latin counterpart, sinus, which means "cove" or "bay". And after that, the sinus became sine in English.
's commentary on Aryabhatiya:
That is, find N = 8x+5 = 9y+4 = 7z+1. It turns out that the smallest value for N is 85. In general, diophantine equations, such as this, can be notoriously difficult. They were discussed extensively in ancient Vedic text Sulba Sutras
, whose more ancient parts might date to 800 BCE. Aryabhata's method of solving such problems is called the (कुट्टक) method. Kuttaka means "pulverizing" or "breaking into small pieces", and the method involves a recursive algorithm for writing the original factors in smaller numbers. Today this algorithm, elaborated by Bhaskara in 621 CE, is the standard method for solving first-order diophantine equations and is often referred to as the Aryabhata algorithm. The diophantine equations are of interest in cryptology, and the RSA Conference
, 2006, focused on the kuttaka method and earlier work in the Sulbasutras.
of squares and cubes: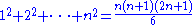
and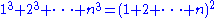
's khanDakhAdyaka. In some texts, he seems to ascribe the apparent motions of the heavens to the Earth's rotation. He may have believed that the planet's orbits as elliptical
rather than circular.
Aryabhata described a geocentric model of the solar system, in which the
Sun and Moon are each carried by epicycles. They in turn revolve around
the Earth. In this model, which is also found in the Paitāmahasiddhānta (c. CE 425), the motions of the planets are each governed by two epicycles, a smaller manda (slow) and a larger śīghra (fast).
The order of the planets in terms of distance from earth is taken as: the Moon
, Mercury
, Venus
, the Sun
, Mars
, Jupiter
, Saturn
, and the asterisms
."
The positions and periods of the planets was calculated relative to uniformly moving points. In the case of Mercury and Venus, they move around the Earth at the same mean speed as the Sun. In the case of Mars, Jupiter, and Saturn, they move around the Earth at specific speeds, representing each planet's motion through the zodiac. Most historians of astronomy consider that this two-epicycle model reflects elements of pre-Ptolemaic Greek astronomy. Another element in Aryabhata's model, the śīghrocca, the basic planetary period in relation to the Sun, is seen by some historians as a sign of an underlying heliocentric model.
and planets shine by reflected sunlight. Instead of the prevailing cosmogony in which eclipses were caused by pseudo-planetary nodes Rahu
and Ketu
, he explains eclipses in terms of shadows cast by and falling on Earth. Thus, the lunar eclipse occurs when the moon enters into the Earth's shadow (verse gola.37). He discusses at length the size and extent of the Earth's shadow (verses gola.38–48) and then provides the computation and the size of the eclipsed part during an eclipse. Later Indian astronomers improved on the calculations, but Aryabhata's methods provided the core. His computational paradigm was so accurate that 18th century scientist Guillaume Le Gentil
, during a visit to Pondicherry, India, found the Indian computations of the duration of the lunar eclipse
of 30 August 1765 to be short by 41 seconds, whereas his charts (by Tobias Mayer, 1752) were long by 68 seconds.
at 365 days, 6 hours, 12 minutes, and 30 seconds (365.25858 days) is an error of 3 minutes and 20 seconds over the length of a year (365.25636 days).
model, in which the planets orbit the Sun, though this has been rebutted. It has also been suggested that aspects of Aryabhata's system may have been derived from an earlier, likely pre-Ptolemaic Greek
, heliocentric model of which Indian astronomers were unaware, though the evidence is scant. The general consensus is that a synodic anomaly (depending on the position of the sun) does not imply a physically heliocentric orbit (such corrections being also present in late Babylonian astronomical texts), and that Aryabhata's system was not explicitly heliocentric.
translation during the Islamic Golden Age
(c. 820 CE), was particularly influential. Some of his results are cited by Al-Khwarizmi and in the 10th century Al-Biruni
stated that Aryabhata's followers believed that the Earth rotated on its axis.
His definitions of sine
(jya), cosine (kojya), versine (utkrama-jya),
and inverse sine (otkram jya) influenced the birth of trigonometry
. He was also the first to specify sine and versine
(1 − cos x) tables, in 3.75° intervals from 0° to 90°, to an accuracy of 4 decimal places.
In fact, modern names "sine" and "cosine" are mistranscriptions of the words jya and kojya as introduced by Aryabhata. As mentioned, they were translated as jiba and kojiba in Arabic and then misunderstood by Gerard of Cremona
while translating an Arabic geometry text to Latin
. He assumed that jiba was the Arabic word jaib, which means "fold in a garment", L. sinus (c. 1150).
Aryabhata's astronomical calculation methods were also very influential.
Along with the trigonometric tables, they came to be widely used in the Islamic world and used to compute many Arabic astronomical tables (zij
es). In particular, the astronomical tables in the work of the Arabic Spain
scientist Al-Zarqali (11th century) were translated into Latin as the Tables of Toledo
(12th c.) and remained the most accurate ephemeris
used in Europe for centuries.
Calendric calculations devised by Aryabhata and his followers have been in continuous use in India for the practical purposes of fixing the Panchangam
(the Hindu calendar
). In the Islamic world, they formed the basis of the Jalali calendar introduced in 1073 CE by a group of astronomers including Omar Khayyam
, versions of which (modified in 1925) are the national calendars in use in Iran
and Afghanistan
today. The dates of the Jalali calendar are based on actual solar transit, as in Aryabhata and earlier Siddhanta
calendars. This type of calendar requires an ephemeris for calculating dates. Although dates were difficult to compute, seasonal errors were less in the Jalali calendar than in the Gregorian calendar
.
India's first satellite Aryabhata
and the lunar crater Aryabhata
are named in his honour. An Institute for conducting research in astronomy, astrophysics and atmospheric sciences is the Aryabhatta Research Institute of Observational Sciences
(ARIES) near Nainital, India. The inter-school Aryabhata Maths Competition is also named after him, as is Bacillus aryabhata, a species of bacteria discovered by ISRO scientists in 2009.
| last=Clark | first=Walter Eugene
| year=1930
| publisher=University of Chicago Press; reprint: Kessinger Publishing (2006)
| isbn=978-1425485993
| url=http://www.archive.org/details/The_Aryabhatiya_of_Aryabhata_Clark_1930
| ref = harv
| postscript =
}}
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
-astronomer
Astronomer
An astronomer is a scientist who studies celestial bodies such as planets, stars and galaxies.Historically, astronomy was more concerned with the classification and description of phenomena in the sky, while astrophysics attempted to explain these phenomena and the differences between them using...
s from the classical age of Indian mathematics
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
and Indian astronomy. His most famous works are the Āryabhaṭīya
Aryabhatiya
Āryabhaṭīya or Āryabhaṭīyaṃ, a Sanskrit astronomical treatise, is the magnum opus and only extant work of the 5th century Indian mathematician, Āryabhaṭa.- Structure and style:...
(499 CE, when he was 23 years old) and the Arya-siddhanta
Siddhanta
Siddhanta, a Sanskrit term, roughly translates as the Doctrine or the Tradition. It denotes the established and accepted view of a particular school within Indian philosophy.-Hindu philosophy:...
.
Name
While there is a tendency to misspell his name as "Aryabhatta" by analogy with other names having the "bhatta" suffix, his name is properly spelled Aryabhata: every astronomical text spells his name thus, including BrahmaguptaBrahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
's references to him "in more than a hundred places by name". Furthermore, in most instances "Aryabhatta" does not fit the metre either.
Time and Place of birth
Aryabhata mentions in the Aryabhatiya that it was composed 3,630 years into the Kali YugaKali Yuga
Kali Yuga is the last of the four stages that the world goes through as part of the cycle of yugas described in the Indian scriptures. The other ages are Satya Yuga, Treta Yuga and Dvapara Yuga...
, when he was 23 years old. This corresponds to 499 CE, and implies that he was born in 476 CE.
Aryabhata provides no information about his place of birth. The only information comes from Bhāskara I
Bhaskara I
Bhāskara was a 7th century Indian mathematician, who was apparently the first to write numbers in the Hindu-Arabic decimal system with a circle for the zero, and who gave a unique and remarkable rational approximation of the sine function in his commentary on Aryabhata's work...
, who describes Aryabhata as āśmakīya, "one belonging to the aśmaka country." The Asmaka were one of the 16 of Ancient Indian Mahajanapadas
Mahajanapadas
Mahājanapadas , literally "great realms", were ancient Indian kingdoms or countries...
, and the only one situated south of the Vindhyas.
It is widely attested that during the mid-first millennium BCE, a branch of the Aśmaka people settled in the region between the Narmada
Narmada River
The Narmada , also called Rewa is a river in central India and the fifth largest river in the Indian subcontinent. It is the third largest river that completely flows within India after Ganges and Godavari...
and Godavari rivers in central India, and it is possible Aryabhata was born there. However, early Buddhist texts describe Ashmaka as being further south, in dakshinapath or the Deccan, while other texts describe the Ashmakas as having fought Alexander.
Many are of the view that he was born in the south of India in Kerala
Kerala
or Keralam is an Indian state located on the Malabar coast of south-west India. It was created on 1 November 1956 by the States Reorganisation Act by combining various Malayalam speaking regions....
and lived in Magadha
Magadha
Magadha formed one of the sixteen Mahājanapadas or kingdoms in ancient India. The core of the kingdom was the area of Bihar south of the Ganga; its first capital was Rajagriha then Pataliputra...
at the time of the Gupta rulers.
Education
It is fairly certain that, at some point, he went to Kusumapura for advanced studies and that he lived there for some time. Both Hindu and Buddhist tradition, as well as Bhāskara IBhaskara I
Bhāskara was a 7th century Indian mathematician, who was apparently the first to write numbers in the Hindu-Arabic decimal system with a circle for the zero, and who gave a unique and remarkable rational approximation of the sine function in his commentary on Aryabhata's work...
(CE 629), identify Kusumapura as Pāṭaliputra, modern Patna
Patna
Paṭnā , is the capital of the Indian state of Bihar and the second largest city in Eastern India . Patna is one of the oldest continuously inhabited places in the world...
. A verse mentions that Aryabhata was the head of an institution () at Kusumapura, and, because the university of Nalanda
Nalanda
Nālandā is the name of an ancient center of higher learning in Bihar, India.The site of Nalanda is located in the Indian state of Bihar, about 55 miles south east of Patna, and was a Buddhist center of learning from the fifth or sixth century CE to 1197 CE. It has been called "one of the...
was in Pataliputra at the time and had an astronomical observatory, it is speculated that Aryabhata might have been the head of the Nalanda university as well. Aryabhata is also reputed to have set up an observatory at the Sun temple in Taregana
Taregana
Taregana or Taregna , is a small town in Bihar, India, about from Patna.-History:In Taregna Aryabhata set up an Astronomical Observatory in the Sun Temple 6th century. It is believed that here he proposed the Heliocentric Model, and suggested for the first time in history that Earth revolves...
, Bihar.
Other hypotheses
Some archeological evidences suggests that Aryabhata could have originated from the present day KodungallurKodungallur
Kodungallur is a municipality in Thrissur District, in the state of Kerala, India on the Malabar Coast. Kodungallur is located about 29 km northwest of Kochi city and 38 km Southwest of Thrissur, on National Highway 17 . Muziris the ancient seaport at the mouth of the Periyar River was...
in Kerala
Kerala
or Keralam is an Indian state located on the Malabar coast of south-west India. It was created on 1 November 1956 by the States Reorganisation Act by combining various Malayalam speaking regions....
region. For instance, one hypothesis was that aśmaka (Sanskrit for "stone") may be the region in Kerala that is now known as Koṭuṅṅallūr, based on the belief that it was earlier known as Koṭum-Kal-l-ūr ("city of hard stones"); however, old records show that the city was actually Koṭum-kol-ūr ("city of strict governance"). Similarly, the fact that several commentaries on the Aryabhatiya have come from Kerala were used to suggest that it was Aryabhata's main place of life and activity; however, many commentaries have come from outside Kerala, and the Aryasiddhanta was completely unknown in Kerala.
Aryabhata mentions "Lanka" on several occasions in the Aryabhatiya, but his "Lanka" is an abstraction, standing for a point on the equator at the same longitude as his Ujjayini.
Works
Aryabhata is the author of several treatises on mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, some of which are lost.
His major work, Aryabhatiya, a compendium of mathematics and astronomy, was extensively referred to in the Indian mathematical literature and has survived to modern times. The mathematical part of the Aryabhatiya covers arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
, algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, plane trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, and spherical trigonometry
Spherical trigonometry
Spherical trigonometry is a branch of spherical geometry which deals with polygons on the sphere and the relationships between the sides and the angles...
. It also contains continued fractions
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
, quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
s, sums-of-power series, and a table of sines
Āryabhaṭa's sine table
Āryabhaṭa's sine table is a set of twenty-four of numbers given in the astronomical treatise Āryabhaṭiya composed by the fifth century Indian mathematician and astronomer Āryabhaṭa , for the computation of the half-chords of certain set of arcs of a circle...
.
The Arya-siddhanta, a lost work on astronomical computations, is known through the writings of Aryabhata's contemporary, Varahamihira
Varahamihira
Varāhamihira , also called Varaha or Mihira, was an Indian astronomer, mathematician, and astrologer who lived in Ujjain...
, and later mathematicians and commentators, including Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
and Bhaskara I
Bhaskara I
Bhāskara was a 7th century Indian mathematician, who was apparently the first to write numbers in the Hindu-Arabic decimal system with a circle for the zero, and who gave a unique and remarkable rational approximation of the sine function in his commentary on Aryabhata's work...
. This work appears to be based on the older Surya Siddhanta
Surya Siddhanta
The Surya Siddhanta is one of the earliest siddhanta in archeo-astronomy of the Hindus by an unknown author. It describes the archeo-astronomy theories, principles and methods of the ancient Hindus. This siddhanta is supposed to be the knowledge that the Sun god gave to an Asura called Maya. Asuras...
and uses the midnight-day reckoning, as opposed to sunrise in Aryabhatiya. It also contained a description of several astronomical instruments: the gnomon
Gnomon
The gnomon is the part of a sundial that casts the shadow. Gnomon is an ancient Greek word meaning "indicator", "one who discerns," or "that which reveals."It has come to be used for a variety of purposes in mathematics and other fields....
(shanku-yantra), a shadow instrument (chhAyA-yantra), possibly angle-measuring devices, semicircular and circular (dhanur-yantra / chakra-yantra), a cylindrical stick yasti-yantra, an umbrella-shaped device called the chhatra-yantra, and water clock
Water clock
A water clock or clepsydra is any timepiece in which time is measured by the regulated flow of liquid into or out from a vessel where the amount is then measured.Water clocks, along with sundials, are likely to be the oldest time-measuring instruments, with the only exceptions...
s of at least two types, bow-shaped and cylindrical.
A third text, which may have survived in the Arabic
Arabic language
Arabic is a name applied to the descendants of the Classical Arabic language of the 6th century AD, used most prominently in the Quran, the Islamic Holy Book...
translation, is Al ntf or Al-nanf. It claims that it is a translation by Aryabhata, but the Sanskrit name of this work is not known.
Probably dating from the 9th century, it is mentioned by the Persian
Persian people
The Persian people are part of the Iranian peoples who speak the modern Persian language and closely akin Iranian dialects and languages. The origin of the ethnic Iranian/Persian peoples are traced to the Ancient Iranian peoples, who were part of the ancient Indo-Iranians and themselves part of...
scholar and chronicler of India, Abū Rayhān al-Bīrūnī.
Aryabhatiya
Direct details of Aryabhata's work are known only from the AryabhatiyaAryabhatiya
Āryabhaṭīya or Āryabhaṭīyaṃ, a Sanskrit astronomical treatise, is the magnum opus and only extant work of the 5th century Indian mathematician, Āryabhaṭa.- Structure and style:...
. The name "Aryabhatiya" is due to later commentators. Aryabhata himself may not have given it a name. His disciple Bhaskara I
Bhaskara I
Bhāskara was a 7th century Indian mathematician, who was apparently the first to write numbers in the Hindu-Arabic decimal system with a circle for the zero, and who gave a unique and remarkable rational approximation of the sine function in his commentary on Aryabhata's work...
calls it Ashmakatantra (or the treatise from the Ashmaka). It is also occasionally referred to as Arya-shatas-aShTa (literally, Aryabhata's 108), because there are 108 verses in the text. It is written in the very terse style typical of sutra
Sutra
Sūtra is an aphorism or a collection of such aphorisms in the form of a manual. Literally it means a thread or line that holds things together and is derived from the verbal root siv-, meaning to sew , as does the medical term...
literature, in which each line is an aid to memory for a complex system. Thus, the explication of meaning is due to commentators. The text consists of the 108 verses and 13 introductory verses, and is divided into four pādas or chapters:
- Gitikapada: (13 verses): large units of time—kalpa, manvantra, and yuga—which present a cosmology different from earlier texts such as Lagadha's Vedanga JyotishaVedanga JyotishaThe ' is an Indian text on Jyotisha, redacted by Lagadha .The text is foundational to the Vedanga discipline of Jyotisha. It is dated to the final centuries BCE...
(c. 1st century BCE). There is also a table of sines (jya), given in a single verse. The duration of the planetary revolutions during a mahayuga is given as 4.32 million years. - Ganitapada (33 verses): covering mensuration (kṣetra vyāvahāra), arithmetic and geometric progressions, gnomonGnomonThe gnomon is the part of a sundial that casts the shadow. Gnomon is an ancient Greek word meaning "indicator", "one who discerns," or "that which reveals."It has come to be used for a variety of purposes in mathematics and other fields....
/ shadows (shanku-chhAyA), simple, quadratic, simultaneousSimultaneous equationsIn mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations...
, and indeterminate equations (kuTTaka) - Kalakriyapada (25 verses): different units of time and a method for determining the positions of planets for a given day, calculations concerning the intercalary month (adhikamAsa), kShaya-tithis, and a seven-day week with names for the days of week.
- Golapada (50 verses): Geometric/trigonometric aspects of the celestial sphereCelestial sphereIn astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
, features of the eclipticEclipticThe ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
, celestial equatorCelestial equatorThe celestial equator is a great circle on the imaginary celestial sphere, in the same plane as the Earth's equator. In other words, it is a projection of the terrestrial equator out into space...
, node, shape of the earth, cause of day and night, rising of zodiacal signs on horizon, etc. In addition, some versions cite a few colophonColophon (publishing)In publishing, a colophon is either:* A brief description of publication or production notes relevant to the edition, in modern books usually located at the reverse of the title page, but can also sometimes be located at the end of the book, or...
s added at the end, extolling the virtues of the work, etc.
The Aryabhatiya presented a number of innovations in mathematics and astronomy in verse form, which were influential for many centuries. The extreme brevity of the text was elaborated in commentaries by his disciple Bhaskara I (Bhashya, c. 600 CE) and by Nilakantha Somayaji
Nilakantha Somayaji
Kelallur Nilakantha Somayaji was a major mathematician and astronomer of the Kerala school of astronomy and mathematics. One of his most influential works was the comprehensive astronomical treatise Tantrasamgraha completed in 1501...
in his Aryabhatiya Bhasya, (1465 CE).
Place value system and zero
The place-value system, first seen in the 3rd century Bakhshali ManuscriptBakhshali Manuscript
The Bakhshali Manuscript is an Ancient Indian mathematical manuscript written on birch bark which was found near the village of Bakhshali in 1881 in what was then the North-West Frontier Province of British India...
, was clearly in place in his work. While he did not use a symbol for zero, the French mathematician Georges Ifrah
Georges Ifrah
Georges Ifrah is a French author and historian of mathematics, especially numerals. He was formerly a teacher of mathematics....
explains that knowledge of zero was implicit in Aryabhata's place-value system as a place holder for the powers of ten with null
Null
-In computing:* Null , a special marker and keyword in SQL* Null character, the zero-valued ASCII character, also designated by NUL, often used as a terminator, separator or filler* Null device, a special computer file that discards all data written to it...
coefficients
However, Aryabhata did not use the Brahmi numerals. Continuing the Sanskrit
Sanskrit
Sanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
ic tradition from Vedic times
Vedic period
The Vedic period was a period in history during which the Vedas, the oldest scriptures of Hinduism, were composed. The time span of the period is uncertain. Philological and linguistic evidence indicates that the Rigveda, the oldest of the Vedas, was composed roughly between 1700–1100 BCE, also...
, he used letters of the alphabet to denote numbers, expressing quantities, such as the table of sines in a mnemonic
Mnemonic
A mnemonic , or mnemonic device, is any learning technique that aids memory. To improve long term memory, mnemonic systems are used to make memorization easier. Commonly encountered mnemonics are often verbal, such as a very short poem or a special word used to help a person remember something,...
form.
Approximation of π
Aryabhata worked on the approximation for piPi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
(
 ), and may have come to the conclusion that
), and may have come to the conclusion that  is irrational. In the second part of the Aryabhatiyam ( 10), he writes:
is irrational. In the second part of the Aryabhatiyam ( 10), he writes:
"Add four to 100, multiply by eight, and then add 62,000. By this rule the circumference of a circle with a diameter of 20,000 can be approached."
This implies that the ratio of the circumference to the diameter is ((4 + 100) × 8 + 62000)/20000 = 62832/20000 = 3.1416, which is accurate to five significant figures
Significant figures
The significant figures of a number are those digits that carry meaning contributing to its precision. This includes all digits except:...
.
It is speculated that Aryabhata used the word āsanna (approaching), to mean that not only is this an approximation but that the value is incommensurable (or irrational). If this is correct, it is quite a sophisticated insight, because the irrationality of pi was proved in Europe only in 1761 by Lambert
Johann Heinrich Lambert
Johann Heinrich Lambert was a Swiss mathematician, physicist, philosopher and astronomer.Asteroid 187 Lamberta was named in his honour.-Biography:...
.
After Aryabhatiya was translated into Arabic
Arabic language
Arabic is a name applied to the descendants of the Classical Arabic language of the 6th century AD, used most prominently in the Quran, the Islamic Holy Book...
(c. 820 CE)
this approximation was mentioned in Al-Khwarizmi's book on algebra.
Trigonometry
In Ganitapada 6, Aryabhata gives the area of a triangle as- tribhujasya phalashariram samadalakoti bhujardhasamvargah
that translates to: "for a triangle, the result of a perpendicular with the half-side is the area."
Aryabhata discussed the concept of sine in his work by the name of ardha-jya. Literally, it means "half-chord". For simplicity, people started calling it jya. When Arabic writers translated his works from Sanskrit
Sanskrit
Sanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
into Arabic, they referred it as jiba. However, in Arabic writings, vowels are omitted, and it was abbreviated as jb. Later writers substituted it with jaib, meaning "pocket" or "fold (in a garment)". (In Arabic, jiba is a meaningless word.) Later in the 12th century, when Gherardo of Cremona translated these writings from Arabic into Latin, he replaced the Arabic jaib with its Latin counterpart, sinus, which means "cove" or "bay". And after that, the sinus became sine in English.
Indeterminate equations
A problem of great interest to Indian mathematicians since ancient times has been to find integer solutions to equations that have the form ax + by = c, a topic that has come to be known as diophantine equations. This is an example from BhāskaraBhaskara I
Bhāskara was a 7th century Indian mathematician, who was apparently the first to write numbers in the Hindu-Arabic decimal system with a circle for the zero, and who gave a unique and remarkable rational approximation of the sine function in his commentary on Aryabhata's work...
's commentary on Aryabhatiya:
- Find the number which gives 5 as the remainder when divided by 8, 4 as the remainder when divided by 9, and 1 as the remainder when divided by 7
That is, find N = 8x+5 = 9y+4 = 7z+1. It turns out that the smallest value for N is 85. In general, diophantine equations, such as this, can be notoriously difficult. They were discussed extensively in ancient Vedic text Sulba Sutras
Sulba Sutras
The Shulba Sutras or Śulbasūtras are sutra texts belonging to the Śrauta ritual and containing geometry related to fire-altar construction.- Purpose and origins :...
, whose more ancient parts might date to 800 BCE. Aryabhata's method of solving such problems is called the (कुट्टक) method. Kuttaka means "pulverizing" or "breaking into small pieces", and the method involves a recursive algorithm for writing the original factors in smaller numbers. Today this algorithm, elaborated by Bhaskara in 621 CE, is the standard method for solving first-order diophantine equations and is often referred to as the Aryabhata algorithm. The diophantine equations are of interest in cryptology, and the RSA Conference
RSA Conference
The RSA Conference is a cryptography and information security-related conference held annually in the San Francisco Bay Area.The RSA Conference started in 1991 as a forum for cryptographers to gather and share the latest knowledge and advancements in the area of Internet security...
, 2006, focused on the kuttaka method and earlier work in the Sulbasutras.
Algebra
In Aryabhatiya Aryabhata provided elegant results for the summation of seriesSeries (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
of squares and cubes:
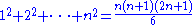
and
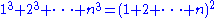
Astronomy
Aryabhata's system of astronomy was called the audAyaka system, in which days are reckoned from uday, dawn at lanka or "equator". Some of his later writings on astronomy, which apparently proposed a second model (or ardha-rAtrikA, midnight) are lost but can be partly reconstructed from the discussion in BrahmaguptaBrahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
's khanDakhAdyaka. In some texts, he seems to ascribe the apparent motions of the heavens to the Earth's rotation. He may have believed that the planet's orbits as elliptical
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
rather than circular.
Motions of the solar system
Aryabhata correctly insisted that the earth rotates about its axis daily, and that the apparent movement of the stars is a relative motion caused by the rotation of the earth, contrary to the then-prevailing view in other parts of the world, that the sky rotated. This is indicated in the first chapter of the Aryabhatiya, where he gives the number of rotations of the earth in a yuga, and made more explicit in his gola chapter:Aryabhata described a geocentric model of the solar system, in which the
Sun and Moon are each carried by epicycles. They in turn revolve around
the Earth. In this model, which is also found in the Paitāmahasiddhānta (c. CE 425), the motions of the planets are each governed by two epicycles, a smaller manda (slow) and a larger śīghra (fast).
The order of the planets in terms of distance from earth is taken as: the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
, Mercury
Mercury (planet)
Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits...
, Venus
Venus
Venus is the second planet from the Sun, orbiting it every 224.7 Earth days. The planet is named after Venus, the Roman goddess of love and beauty. After the Moon, it is the brightest natural object in the night sky, reaching an apparent magnitude of −4.6, bright enough to cast shadows...
, the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
, Mars
Mars
Mars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance...
, Jupiter
Jupiter
Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,...
, Saturn
Saturn
Saturn is the sixth planet from the Sun and the second largest planet in the Solar System, after Jupiter. Saturn is named after the Roman god Saturn, equated to the Greek Cronus , the Babylonian Ninurta and the Hindu Shani. Saturn's astronomical symbol represents the Roman god's sickle.Saturn,...
, and the asterisms
Asterism (astronomy)
In astronomy, an asterism is a pattern of stars recognized on Earth's night sky. It may form part of an official constellation, or be composed of stars from more than one. Like constellations, asterisms are in most cases composed of stars which, while they are visible in the same general direction,...
."
The positions and periods of the planets was calculated relative to uniformly moving points. In the case of Mercury and Venus, they move around the Earth at the same mean speed as the Sun. In the case of Mars, Jupiter, and Saturn, they move around the Earth at specific speeds, representing each planet's motion through the zodiac. Most historians of astronomy consider that this two-epicycle model reflects elements of pre-Ptolemaic Greek astronomy. Another element in Aryabhata's model, the śīghrocca, the basic planetary period in relation to the Sun, is seen by some historians as a sign of an underlying heliocentric model.
Eclipses
Solar and lunar eclipses were scientifically explained by Aryabhata. Aryabhata states that the MoonMoon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
and planets shine by reflected sunlight. Instead of the prevailing cosmogony in which eclipses were caused by pseudo-planetary nodes Rahu
Rahu
In Hindu mythology, Rahu is a cut-off head of an asura, that swallows the sun or the moon causing eclipses. He is depicted in art as a serpent with no body riding a chariot drawn by eight black horses. Rahu is one of the navagrahas in Vedic astrology...
and Ketu
Ketu (mythology)
Ketu is the descending lunar node. 'Ketu' is said to be the body of Rahu, after the head of the asura was cut off by God Vishnu. In Hindu mythology, Ketu is generally referred to as a "shadow" planet. It is believed to have a tremendous impact on human lives and also the whole creation...
, he explains eclipses in terms of shadows cast by and falling on Earth. Thus, the lunar eclipse occurs when the moon enters into the Earth's shadow (verse gola.37). He discusses at length the size and extent of the Earth's shadow (verses gola.38–48) and then provides the computation and the size of the eclipsed part during an eclipse. Later Indian astronomers improved on the calculations, but Aryabhata's methods provided the core. His computational paradigm was so accurate that 18th century scientist Guillaume Le Gentil
Guillaume Le Gentil
Guillaume Joseph Hyacinthe Jean-Baptiste Le Gentil de la Galaisière was a French astronomer.-Biography:...
, during a visit to Pondicherry, India, found the Indian computations of the duration of the lunar eclipse
Lunar eclipse
A lunar eclipse occurs when the Moon passes behind the Earth so that the Earth blocks the Sun's rays from striking the Moon. This can occur only when the Sun, Earth, and Moon are aligned exactly, or very closely so, with the Earth in the middle. Hence, a lunar eclipse can only occur the night of a...
of 30 August 1765 to be short by 41 seconds, whereas his charts (by Tobias Mayer, 1752) were long by 68 seconds.
Sidereal periods
Considered in modern English units of time, Aryabhata calculated the sidereal rotation (the rotation of the earth referencing the fixed stars) as 23 hours, 56 minutes, and 4.1 seconds; the modern value is 23:56:4.091. Similarly, his value for the length of the sidereal yearSidereal year
A sidereal year is the time taken by the Earth to orbit the Sun once with respect to the fixed stars. Hence it is also the time taken for the Sun to return to the same position with respect to the fixed stars after apparently travelling once around the ecliptic. It was equal to at noon 1 January...
at 365 days, 6 hours, 12 minutes, and 30 seconds (365.25858 days) is an error of 3 minutes and 20 seconds over the length of a year (365.25636 days).
Heliocentrism
As mentioned, Aryabhata advocated an astronomical model in which the Earth turns on its own axis. His model also gave corrections (the śīgra anomaly) for the speeds of the planets in the sky in terms of the mean speed of the sun. Thus, it has been suggested that Aryabhata's calculations were based on an underlying heliocentricHeliocentrism
Heliocentrism, or heliocentricism, is the astronomical model in which the Earth and planets revolve around a stationary Sun at the center of the universe. The word comes from the Greek . Historically, heliocentrism was opposed to geocentrism, which placed the Earth at the center...
model, in which the planets orbit the Sun, though this has been rebutted. It has also been suggested that aspects of Aryabhata's system may have been derived from an earlier, likely pre-Ptolemaic Greek
Greek astronomy
Greek astronomy is astronomy written in the Greek language in classical antiquity. Greek astronomy is understood to include the ancient Greek, Hellenistic, Greco-Roman, and Late Antiquity eras. It is not limited geographically to Greece or to ethnic Greeks, as the Greek language had become the...
, heliocentric model of which Indian astronomers were unaware, though the evidence is scant. The general consensus is that a synodic anomaly (depending on the position of the sun) does not imply a physically heliocentric orbit (such corrections being also present in late Babylonian astronomical texts), and that Aryabhata's system was not explicitly heliocentric.
Legacy
Aryabhata's work was of great influence in the Indian astronomical tradition and influenced several neighbouring cultures through translations. The ArabicArabic language
Arabic is a name applied to the descendants of the Classical Arabic language of the 6th century AD, used most prominently in the Quran, the Islamic Holy Book...
translation during the Islamic Golden Age
Islamic Golden Age
During the Islamic Golden Age philosophers, scientists and engineers of the Islamic world contributed enormously to technology and culture, both by preserving earlier traditions and by adding their own inventions and innovations...
(c. 820 CE), was particularly influential. Some of his results are cited by Al-Khwarizmi and in the 10th century Al-Biruni
Al-Biruni
Abū al-Rayḥān Muḥammad ibn Aḥmad al-BīrūnīArabic spelling. . The intermediate form Abū Rayḥān al-Bīrūnī is often used in academic literature...
stated that Aryabhata's followers believed that the Earth rotated on its axis.
His definitions of sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
(jya), cosine (kojya), versine (utkrama-jya),
and inverse sine (otkram jya) influenced the birth of trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
. He was also the first to specify sine and versine
Versine
The versine or versed sine, versin, is a trigonometric function equal to and 2sin2. It appeared in some of the earliest trigonometric tables and was once widespread, but it is now little-used...
(1 − cos x) tables, in 3.75° intervals from 0° to 90°, to an accuracy of 4 decimal places.
In fact, modern names "sine" and "cosine" are mistranscriptions of the words jya and kojya as introduced by Aryabhata. As mentioned, they were translated as jiba and kojiba in Arabic and then misunderstood by Gerard of Cremona
Gerard of Cremona
Gerard of Cremona was an Italian translator of Arabic scientific works found in the abandoned Arab libraries of Toledo, Spain....
while translating an Arabic geometry text to Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
. He assumed that jiba was the Arabic word jaib, which means "fold in a garment", L. sinus (c. 1150).
Aryabhata's astronomical calculation methods were also very influential.
Along with the trigonometric tables, they came to be widely used in the Islamic world and used to compute many Arabic astronomical tables (zij
Zij
Zīj is the generic name applied to Islamic astronomical books that tabulate parameters used for astronomical calculations of the positions of the Sun, Moon, stars, and planets. The name is derived from the Middle Persian term zih or zīg, meaning cord...
es). In particular, the astronomical tables in the work of the Arabic Spain
Al-Andalus
Al-Andalus was the Arabic name given to a nation and territorial region also commonly referred to as Moorish Iberia. The name describes parts of the Iberian Peninsula and Septimania governed by Muslims , at various times in the period between 711 and 1492, although the territorial boundaries...
scientist Al-Zarqali (11th century) were translated into Latin as the Tables of Toledo
Tables of Toledo
The Toledan Tables, or Tables of Toledo, were astronomical tables which were used to predict the movements of the Sun, Moon and planets relative to the fixed stars...
(12th c.) and remained the most accurate ephemeris
Ephemeris
An ephemeris is a table of values that gives the positions of astronomical objects in the sky at a given time or times. Different kinds of ephemerides are used for astronomy and astrology...
used in Europe for centuries.
Calendric calculations devised by Aryabhata and his followers have been in continuous use in India for the practical purposes of fixing the Panchangam
Panchangam
A panchāngam is a Hindu astrological almanac, which follows traditional Indian cosmology, and presents important astronomical data in tabulated form. It is sometimes spelled Pancanga, Panchanga, Panchaanga, or Panchānga, and is pronounced Panchānga...
(the Hindu calendar
Hindu calendar
The hindu calendar used in ancient times has undergone many changes in the process of regionalization, and today there are several regional Indian calendars, as well as an Indian national calendar. Nepali calendar, Bengali calendar, Malayalam calendar, Tamil calendar, Telugu calendar, Kannada...
). In the Islamic world, they formed the basis of the Jalali calendar introduced in 1073 CE by a group of astronomers including Omar Khayyam
Omar Khayyám
Omar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....
, versions of which (modified in 1925) are the national calendars in use in Iran
Iran
Iran , officially the Islamic Republic of Iran , is a country in Southern and Western Asia. The name "Iran" has been in use natively since the Sassanian era and came into use internationally in 1935, before which the country was known to the Western world as Persia...
and Afghanistan
Afghanistan
Afghanistan , officially the Islamic Republic of Afghanistan, is a landlocked country located in the centre of Asia, forming South Asia, Central Asia and the Middle East. With a population of about 29 million, it has an area of , making it the 42nd most populous and 41st largest nation in the world...
today. The dates of the Jalali calendar are based on actual solar transit, as in Aryabhata and earlier Siddhanta
Siddhanta
Siddhanta, a Sanskrit term, roughly translates as the Doctrine or the Tradition. It denotes the established and accepted view of a particular school within Indian philosophy.-Hindu philosophy:...
calendars. This type of calendar requires an ephemeris for calculating dates. Although dates were difficult to compute, seasonal errors were less in the Jalali calendar than in the Gregorian calendar
Gregorian calendar
The Gregorian calendar, also known as the Western calendar, or Christian calendar, is the internationally accepted civil calendar. It was introduced by Pope Gregory XIII, after whom the calendar was named, by a decree signed on 24 February 1582, a papal bull known by its opening words Inter...
.
India's first satellite Aryabhata
Aryabhata (satellite)
Aryabhatta was India's first satellite, named after the great Indian astronomer of the same name. It was launched by the Soviet Union on 19 April 1975 from Kapustin Yar using a Cosmos-3M launch vehicle. It was built by the Indian Space Research Organization to gain experience in building and...
and the lunar crater Aryabhata
Aryabhata (crater)
Aryabhata, named after Indian astronomer Aryabhata , is the remnant of a lunar impact crater located in the eastern Mare Tranquillitatis. The crater has been almost submerged by lava-flow, and now only an arc-shaped ridge formed from the eastern half of the rim remains above the lunar mare. This...
are named in his honour. An Institute for conducting research in astronomy, astrophysics and atmospheric sciences is the Aryabhatta Research Institute of Observational Sciences
Aryabhatta Research Institute of Observational Sciences
Aryabhatta Research Institute of Observational Sciences is one of the leading research Institutes which specializes in Astronomy, Astrophysics and Atmospheric Sciences...
(ARIES) near Nainital, India. The inter-school Aryabhata Maths Competition is also named after him, as is Bacillus aryabhata, a species of bacteria discovered by ISRO scientists in 2009.
See also
- AryabhatiyaAryabhatiyaĀryabhaṭīya or Āryabhaṭīyaṃ, a Sanskrit astronomical treatise, is the magnum opus and only extant work of the 5th century Indian mathematician, Āryabhaṭa.- Structure and style:...
- Aryabhata's sine tableĀryabhaṭa's sine tableĀryabhaṭa's sine table is a set of twenty-four of numbers given in the astronomical treatise Āryabhaṭiya composed by the fifth century Indian mathematician and astronomer Āryabhaṭa , for the computation of the half-chords of certain set of arcs of a circle...
- Indian mathematicsIndian mathematicsIndian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
- List of Indian mathematicians
Other references
of : An Ancient Indian Work on Mathematics and Astronomy| last=Clark | first=Walter Eugene
| year=1930
| publisher=University of Chicago Press; reprint: Kessinger Publishing (2006)
| isbn=978-1425485993
| url=http://www.archive.org/details/The_Aryabhatiya_of_Aryabhata_Clark_1930
| ref = harv
| postscript =
}}
- Kak, Subhash C.Subhash KakSubhash Kak is an Indian American computer scientist, most notable for his controversial Indological publications on history, the philosophy of science, ancient astronomy, and the history of mathematics...
(2000). 'Birth and Early Development of Indian Astronomy'. In- Shukla, Kripa Shankar. Aryabhata: Indian Mathematician and Astronomer. New Delhi: Indian National Science Academy, 1976.
External links
- Eugene C. Clark's 1930 English translation of The Aryabhatiya at scribd.com
- Eugene C. Clark's 1930 English translation of The Aryabhatiya in various formats at the Internet Archive. (PDF version)
- http://www.cse.iitk.ac.in/~amit/story/19_aryabhata.htmlAryabhata and Diophantus' son, Hindustan TimesHindustan TimesHindustan Times is an Indian English-language daily newspaper founded in 1924 with roots in the Indian independence movement of the period ....
Storytelling Science column, Nov 2004] - http://www.hindu.com/2007/06/25/stories/2007062558250400.htm
- http://www.wilbourhall.org/ (Surya Siddhanta translations)

