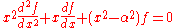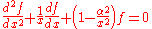Regular singular point
Encyclopedia
In mathematics
, in the theory of ordinary differential equations in the complex plane
 , the points of
, the points of  are classified into ordinary points, at which the equation's coefficients are analytic function
are classified into ordinary points, at which the equation's coefficients are analytic function
s, and singular points, at which some coefficient has a singularity
. Then amongst singular points, an important distinction is made between a regular singular point, where the growth of solutions is bounded (in any small sector) by an algebraic function, and an irregular singular point, where the full solution set requires functions with higher growth rates. This distinction occurs, for example, between the hypergeometric equation, with three regular singular points, and the Bessel equation which is in a sense a limiting case, but where the analytic properties are substantially different.
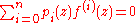
with pi (z) meromorphic functions. One can assume that
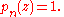
If this is not the case the equation above has to be divided by pn(x). This may introduce singular points to consider.
The equation should be studied on the Riemann sphere
to include the point at infinity as a possible singular point. A Möbius transformation may be applied to move ∞ into the finite part of the complex plane if required, see example on Bessel differential equation below.
Then the Frobenius method
based on the indicial equation may be applied to find possible solutions that are power series times complex powers (z − a)r
near any given a in the complex plane where r need not be an integer; this function may exist, therefore, only thanks to a branch cut extending out from a, or on a Riemann surface
of some punctured disc around a. This presents no difficulty for a an ordinary point (Lazarus Fuchs
1866). When a is a regular singular point, which by definition means that
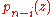
has a pole of order at most i at a, the Frobenius method also can be made to work and provide n independent solutions near a.
Otherwise the point a is an irregular singularity. In that case the monodromy group relating solutions by analytic continuation
has less to say in general, and the solutions are harder to study, except in terms of their asymptotic expansions.
The regularity condition is a kind of Newton polygon
condition, in the sense that the allowed poles are in a region, when plotted against i, bounded by a line at 45° to the axes.
An ordinary differential equation
whose only singular points, including the point at infinity, are regular singular points is called a Fuchsian ordinary differential equation.
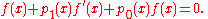
One distinguishes the following cases:
Listed below are several examples from ordinary differential equations from mathematical physics that have singular points and known solutions.
in cylindrical coordinates:
for an arbitrary real or complex number α (the order of the Bessel function
). The most common and important special case is where α is an integer
n.
Dividing this equation by x2 gives:
In this case p1(x) = 1/x has a pole of first order at x = 0.
When α ≠ 0 p0(x) = (1 − α2/x2) has a pole of second order at x = 0. Thus this equation has a regular singularity at 0.
To see what happens when x → ∞ one has to use a Möbius transformation, for example x = 1 / (w - b). After performing the algebra:
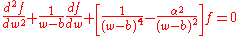
Now
has a pole of first order at w = b. And p0(w) has a pole of fourth order at w = b. Thus this equation has an irregular singularity w = b corresponding to x at ∞. There is a basis for solutions of this differential equation that are Bessel functions.
in spherical coordinates:
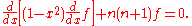
Opening the square bracket gives:
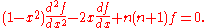
And dividing by (1 - x2):
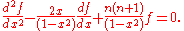
This differential equation has regular singular points at -1, +1, and ∞.
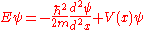
for a harmonic oscillator
. In this case the potential energy V(x) is:
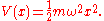
This leads to the following ordinary second order differential equation is:
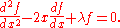
This differential equation has an irregular singularity at ∞. Its solutions are Hermite polynomials
.
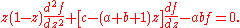
Dividing both sides by z (1 - z) gives:
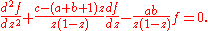
This differential equation has regular singular points at 0, 1 and ∞. A solution is the hypergeometric function.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the theory of ordinary differential equations in the complex plane
Complex differential equation
A complex differential equation is a differential equation whose solutions are functions of a complex variable.Constructing integrals involves choice of what path to take, which means singularities and branch points of the equation need to be studied...
 , the points of
, the points of  are classified into ordinary points, at which the equation's coefficients are analytic function
are classified into ordinary points, at which the equation's coefficients are analytic functionAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s, and singular points, at which some coefficient has a singularity
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
. Then amongst singular points, an important distinction is made between a regular singular point, where the growth of solutions is bounded (in any small sector) by an algebraic function, and an irregular singular point, where the full solution set requires functions with higher growth rates. This distinction occurs, for example, between the hypergeometric equation, with three regular singular points, and the Bessel equation which is in a sense a limiting case, but where the analytic properties are substantially different.
Formal definitions
More precisely, consider an ordinary linear differential equation of n-th order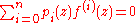
with pi (z) meromorphic functions. One can assume that
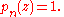
If this is not the case the equation above has to be divided by pn(x). This may introduce singular points to consider.
The equation should be studied on the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
to include the point at infinity as a possible singular point. A Möbius transformation may be applied to move ∞ into the finite part of the complex plane if required, see example on Bessel differential equation below.
Then the Frobenius method
Frobenius method
In mathematics, the Frobenius method, named after Ferdinand Georg Frobenius, is a way to find an infinite series solution for a second-order ordinary differential equation of the formin the vicinity of the regular singular point z=0....
based on the indicial equation may be applied to find possible solutions that are power series times complex powers (z − a)r
near any given a in the complex plane where r need not be an integer; this function may exist, therefore, only thanks to a branch cut extending out from a, or on a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
of some punctured disc around a. This presents no difficulty for a an ordinary point (Lazarus Fuchs
Lazarus Fuchs
Lazarus Immanuel Fuchs was a German mathematician who contributed important research in the field of linear differential equations...
1866). When a is a regular singular point, which by definition means that
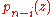
has a pole of order at most i at a, the Frobenius method also can be made to work and provide n independent solutions near a.
Otherwise the point a is an irregular singularity. In that case the monodromy group relating solutions by analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
has less to say in general, and the solutions are harder to study, except in terms of their asymptotic expansions.
The regularity condition is a kind of Newton polygon
Newton polygon
In mathematics, the Newton polygon is a tool for understanding the behaviour of polynomials over local fields.In the original case, the local field of interest was the field of formal Laurent series in the indeterminate X, i.e. the field of fractions of the formal power series ringover K, where K...
condition, in the sense that the allowed poles are in a region, when plotted against i, bounded by a line at 45° to the axes.
An ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
whose only singular points, including the point at infinity, are regular singular points is called a Fuchsian ordinary differential equation.
Examples for second order differential equations
In this case the equation above is reduced to: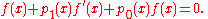
One distinguishes the following cases:
- Point a is an ordinary point when functions p1(x) and p0(x) are analytic at x = a.
- Point a is a regular singular point if p1(x) has a pole up to order 1 at x = a and p0 has a pole of order up to 2 at x = a.
- Otherwise point a is an irregular singular point.
Listed below are several examples from ordinary differential equations from mathematical physics that have singular points and known solutions.
Bessel differential equation
This is an ordinary differential equation of second order. It is found in the solution to Laplace's equationLaplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
in cylindrical coordinates:
for an arbitrary real or complex number α (the order of the Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
). The most common and important special case is where α is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n.
Dividing this equation by x2 gives:
In this case p1(x) = 1/x has a pole of first order at x = 0.
When α ≠ 0 p0(x) = (1 − α2/x2) has a pole of second order at x = 0. Thus this equation has a regular singularity at 0.
To see what happens when x → ∞ one has to use a Möbius transformation, for example x = 1 / (w - b). After performing the algebra:
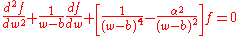
Now
- p1(w) = 1/(w − b)
has a pole of first order at w = b. And p0(w) has a pole of fourth order at w = b. Thus this equation has an irregular singularity w = b corresponding to x at ∞. There is a basis for solutions of this differential equation that are Bessel functions.
Legendre differential equation
This is an ordinary differential equation of second order. It is found in the solution of Laplace's equationLaplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
in spherical coordinates:
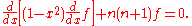
Opening the square bracket gives:
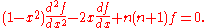
And dividing by (1 - x2):
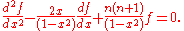
This differential equation has regular singular points at -1, +1, and ∞.
Hermite differential equation
One encounters this ordinary second order differential equation in solving the one dimensional time independent Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
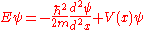
for a harmonic oscillator
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
. In this case the potential energy V(x) is:
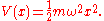
This leads to the following ordinary second order differential equation is:
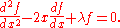
This differential equation has an irregular singularity at ∞. Its solutions are Hermite polynomials
Hermite polynomials
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, such as the Edgeworth series; in combinatorics, as an example of an Appell sequence, obeying the umbral calculus; in numerical analysis as Gaussian quadrature; and in physics, where...
.
Hypergeometric equation
The equation may be defined as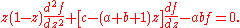
Dividing both sides by z (1 - z) gives:
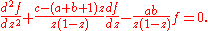
This differential equation has regular singular points at 0, 1 and ∞. A solution is the hypergeometric function.