Doubling the cube
Encyclopedia
Doubling the cube is one of the three most famous geometric problems unsolvable by compass and straightedge construction. It was known to the Egyptians
, Greeks
, and Indians
.
To "double the cube" means to be given a cube
of some side length s and volume V= s3, and to construct a new cube, larger than the first, with volume 2V and therefore side length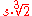
. The problem is known to be impossible to solve with only compass and straightedge
, because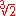
≈ 1.25992105 is not a constructible number
.
, who consulted the oracle at Delphi
in order to learn how to defeat a plague sent by Apollo
. According to Plutarch
it was the citizens of Delos who consulted the oracle at Delphi, seeking a solution for their internal political problems at the time, which had intensified relationships among the citizens. The oracle responded that they must double the size of the altar to Apollo, which was a regular cube. The answer seemed strange to the Delians and they consulted Plato
, who was able to interpret the oracle as the mathematical problem of doubling the volume of a given cube, thus explaining the oracle as the advice of Apollo for the citizens of Delos to occupy themselves with the study of geometry and mathematics in order to calm down their passions.
According to Plutarch, Plato gave the problem to Eudoxus
and Archytas
and Menaechmus
who solved the problem using mechanical means, earning a rebuke from Plato for not solving the problem using pure geometry (Plut., Quaestiones convivales VIII.ii, 718ef). This may be why the problem is referred to in the 350s BC by the author of the pseudo-Platonic Sisyphus
(388e) as still unsolved. However another version of the story says that all three found solutions but they were too abstract to be of practical value.
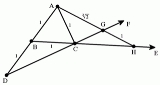
A significant development in finding a solution to the problem was the discovery by Hippocrates of Chios
that it is equivalent to finding two mean proportionals between a line segment and another with twice the length. In modern notation, this means that given segments of lengths a and 2a, the duplication of the cube is equivalent to finding segments of lengths r and s so that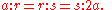
Pierre Wantzel
proved in 1837 that the cube root of 2 is not constructible
; that is, that it cannot be constructed with ruler and compass.
, the conchoid of Nicomedes
, or the Philo line
. Archytas
solved the problem in the fourth century B.C. using geometric construction in three dimensions, determining a certain point as the intersection of three surfaces of revolution.
False claims of doubling the cube with compass and straightedge abound in mathematical crank
literature (pseudomathematics
).
Origami may also be used to construct the cube root of two by folding paper.
homas Heath.
Egyptian mathematics
Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt from ca. 3000 BC to ca. 300 BC.-Overview:Written evidence of the use of mathematics dates back to at least 3000 BC with the ivory labels found at Tomb Uj at Abydos. These labels appear to have been used as tags for...
, Greeks
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
, and Indians
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
.
To "double the cube" means to be given a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
of some side length s and volume V= s3, and to construct a new cube, larger than the first, with volume 2V and therefore side length
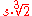. The problem is known to be impossible to solve with only compass and straightedgeCompass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
, because
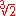≈ 1.25992105 is not a constructible numberConstructible number
A point in the Euclidean plane is a constructible point if, given a fixed coordinate system , the point can be constructed with unruled straightedge and compass...
.
History
The problem owes its name to a story concerning the citizens of DelosDelos
The island of Delos , isolated in the centre of the roughly circular ring of islands called the Cyclades, near Mykonos, is one of the most important mythological, historical and archaeological sites in Greece...
, who consulted the oracle at Delphi
Delphi
Delphi is both an archaeological site and a modern town in Greece on the south-western spur of Mount Parnassus in the valley of Phocis.In Greek mythology, Delphi was the site of the Delphic oracle, the most important oracle in the classical Greek world, and a major site for the worship of the god...
in order to learn how to defeat a plague sent by Apollo
Apollo
Apollo is one of the most important and complex of the Olympian deities in Greek and Roman mythology...
. According to Plutarch
Plutarch
Plutarch then named, on his becoming a Roman citizen, Lucius Mestrius Plutarchus , c. 46 – 120 AD, was a Greek historian, biographer, essayist, and Middle Platonist known primarily for his Parallel Lives and Moralia...
it was the citizens of Delos who consulted the oracle at Delphi, seeking a solution for their internal political problems at the time, which had intensified relationships among the citizens. The oracle responded that they must double the size of the altar to Apollo, which was a regular cube. The answer seemed strange to the Delians and they consulted Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
, who was able to interpret the oracle as the mathematical problem of doubling the volume of a given cube, thus explaining the oracle as the advice of Apollo for the citizens of Delos to occupy themselves with the study of geometry and mathematics in order to calm down their passions.
According to Plutarch, Plato gave the problem to Eudoxus
Eudoxus of Cnidus
Eudoxus of Cnidus was a Greek astronomer, mathematician, scholar and student of Plato. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus's poem on astronomy...
and Archytas
Archytas
Archytas was an Ancient Greek philosopher, mathematician, astronomer, statesman, and strategist. He was a scientist of the Pythagorean school and famous for being the reputed founder of mathematical mechanics, as well as a good friend of Plato....
and Menaechmus
Menaechmus
Menaechmus was an ancient Greek mathematician and geometer born in Alopeconnesus in the Thracian Chersonese, who was known for his friendship with the renowned philosopher Plato and for his apparent discovery of conic sections and his solution to the then-long-standing problem of doubling the cube...
who solved the problem using mechanical means, earning a rebuke from Plato for not solving the problem using pure geometry (Plut., Quaestiones convivales VIII.ii, 718ef). This may be why the problem is referred to in the 350s BC by the author of the pseudo-Platonic Sisyphus
Sisyphus (dialogue)
The Sisyphus is purported to be one of the dialogues of Plato. The dialogue is extant and was included in the Stephanus edition published in Geneva in 1578. It is now generally acknowledged to be spurious. The work dates from the fourth century BC, and the author was presumably a pupil of Plato.It...
(388e) as still unsolved. However another version of the story says that all three found solutions but they were too abstract to be of practical value.
A significant development in finding a solution to the problem was the discovery by Hippocrates of Chios
Hippocrates of Chios
Hippocrates of Chios was an ancient Greek mathematician, , and astronomer, who lived c. 470 – c. 410 BCE.He was born on the isle of Chios, where he originally was a merchant. After some misadventures he went to Athens, possibly for litigation...
that it is equivalent to finding two mean proportionals between a line segment and another with twice the length. In modern notation, this means that given segments of lengths a and 2a, the duplication of the cube is equivalent to finding segments of lengths r and s so that
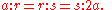
Pierre Wantzel
Pierre Wantzel
Pierre Laurent Wantzel was a French mathematician who proved that several ancient geometric problems were impossible to solve using only compass and straightedge....
proved in 1837 that the cube root of 2 is not constructible
Constructible number
A point in the Euclidean plane is a constructible point if, given a fixed coordinate system , the point can be constructed with unruled straightedge and compass...
; that is, that it cannot be constructed with ruler and compass.
Solutions
Menaechmus' original solution involves the intersection of two conic curves. Other more complicated methods of doubling the cube involve the cissoid of DioclesCissoid of Diocles
In geometry, the cissoid of Diocles is a cubic plane curve notable for the property that it can be used to construct two mean proportionals to a given ratio. In particular, it can be used to double a cube. It can be defined as the cissoid of a circle and a line tangent to it with respect to the...
, the conchoid of Nicomedes
Conchoid (mathematics)
A conchoid is a curve derived from a fixed point O, another curve, and a length d. For every line through O that intersects the given curve at A the two points on the line which are d from A are on the conchoid. The conchoid is, therefore, the cissoid of a circle with center O and the given curve...
, or the Philo line
Philo line
In geometry, the Philo line is a line segment defined from an angle and a point. The Philo line for a point P that lies inside an angle with edges d and e is the shortest line segment that passes through P and has its endpoints on d and e...
. Archytas
Archytas
Archytas was an Ancient Greek philosopher, mathematician, astronomer, statesman, and strategist. He was a scientist of the Pythagorean school and famous for being the reputed founder of mathematical mechanics, as well as a good friend of Plato....
solved the problem in the fourth century B.C. using geometric construction in three dimensions, determining a certain point as the intersection of three surfaces of revolution.
False claims of doubling the cube with compass and straightedge abound in mathematical crank
Crank (person)
"Crank" is a pejorative term used for a person who unshakably holds a belief that most of his or her contemporaries consider to be false. A "cranky" belief is so wildly at variance with commonly accepted belief as to be ludicrous...
literature (pseudomathematics
Pseudomathematics
Pseudomathematics is a form of mathematics-like activity that does not work within the framework, definitions, rules, or rigor of formal mathematical models...
).
Origami may also be used to construct the cube root of two by folding paper.
External links
- Doubling the cube. J. J. O'Connor and E. F. Robertson in the MacTutor History of Mathematics archive.
- To Double a Cube – The Solution of Archytas. Excerpted with permission from A History of Greek Mathematics by Sir T
homas Heath.
- Delian Problem Solved. Or Is It? at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
.