
Mathematical proof
Encyclopedia
In mathematics
, a proof is a convincing demonstration (within the accepted standards of the field) that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning
, rather than from inductive
or empirical
arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single exception. An unproven proposition that is believed to be true is known as a conjecture
.
The statement that is proved is often called a theorem
. Once a theorem is proved, it can be used as the basis to prove further statements. A theorem may also be referred to as a lemma
, especially if it is intended for use as a stepping stone in the proof of another theorem.
Proofs employ logic
but usually include some amount of natural language
which usually admits some ambiguity. In fact, the vast majority of proofs in written mathematics can be considered as applications of rigorous informal logic
. Purely formal proof
s, written in symbolic language instead of natural language, are considered in proof theory
. The distinction between formal and informal proofs has led to much examination of current and historical mathematical practice
, quasi-empiricism in mathematics
, and so-called folk mathematics (in both senses of that term). The philosophy of mathematics
is concerned with the role of language and logic in proofs, and mathematics as a language
.
Plausibility arguments using heuristic devices such as pictures and analogies preceded strict mathematical proof. It is probable that the idea of demonstrating a conclusion first arose in connection with geometry
, which originally meant the same as "land measurement". The development of mathematical proof is primarily the product of ancient Greek mathematics
, and one of its greatest achievements. Thales
(624–546 BCE) proved some theorems in geometry. Eudoxus
(408–355 BCE) and Theaetetus
(417–369 BCE) formulated theorems but did not prove them. Aristotle
(384–322 BCE) said definitions should describe the concept being defined in terms of other concepts already known. Mathematical proofs were revolutionized by Euclid
(300 BCE), who introduced the axiomatic method still in use today, starting with undefined terms and axioms (propositions regarding the undefined terms assumed to be self-evidently true from the Greek “axios” meaning “something worthy”), and used these to prove theorems using deductive logic. His book, the Elements
, was read by anyone who was considered educated in the West until the middle of the 20th century. In addition to the familiar theorems of geometry, such as the Pythagorean theorem
, the Elements includes a proof that the square root of two is irrational and that there are infinitely many prime numbers.
Further advances took place in medieval Islamic mathematics. While earlier Greek proofs were largely geometric demonstrations, the development of arithmetic
and algebra
by Islamic mathematicians allowed more general proofs that no longer depended on geometry. In the 10th century CE, the Iraqi
mathematician Al-Hashimi provided general proofs for numbers (rather than geometric demonstrations) as he considered multiplication, division, etc. for ”lines.” He used this method to provide a proof of the existence of irrational number
s. An inductive proof
for arithmetic sequences
was introduced in the Al-Fakhri (1000) by Al-Karaji
, who used it to prove the binomial theorem
and properties of Pascal's triangle
. Alhazen also developed the method of proof by contradiction, as the first attempt at proving the Euclidean
parallel postulate
.
Modern proof theory
treats proofs as inductively defined data structures. There is no longer an assumption that axioms are "true" in any sense; this allows for parallel mathematical theories built on alternate sets of axioms (see Axiomatic set theory and Non-Euclidean geometry
for examples).
In logic, a formal proof
is not written in a natural language, but instead uses a formal language
consisting of certain strings of symbols from a fixed alphabet. This allows the definition of a formal proof to be precisely specified without any ambiguity. The field of proof theory
studies formal proofs and their properties. Although each informal proof can, in theory, be converted into a formal proof, this is rarely done in practice. The study of formal proofs is used to determine properties of in general, and to show that certain undecidable statement
s are not provable.
A classic question in philosophy asks whether mathematical proofs are analytic or synthetic. Kant, who introduced the analytic-synthetic distinction, believed mathematical proofs are synthetic.
Proofs may be viewed as aesthetic objects, admired for their mathematical beauty
. The mathematician Paul Erdős
was known for describing proofs he found particularly elegant as coming from "The Book", a hypothetical tome containing the most beautiful method(s) of proving each theorem. The book Proofs from THE BOOK
, published in 2003, is devoted to presenting 32 proofs its editors find particularly pleasing.
integer
s is always even:
This proof uses definition of even integers, as well as distribution law
.
. Infinite descent can be used to prove the irrationality of the square root of two.
The principle of mathematical induction states that:
Let N = { 1, 2, 3, 4, ... } be the set of natural numbers and P(n) be a mathematical statement involving the natural number n belonging to N such that
Then P(n) is true for all natural numbers n.
Mathematicians often use the term "proof by induction" as shorthand for a proof by mathematical induction. However, the term "proof by induction" may also be used in logic to mean an argument that uses inductive reasoning
.
establishes the conclusion "if p then q" by proving the equivalent contrapositive statement "if not q then not p".
Example:
If x is odd (not even) then x = 2k + 1 for an integer k.
Thus x² = (2k + 1)² = 4k² + 4k + 1 = 2(2k² + 2k) + 1, where (2k² + 2k) is an integer.
Therefore x² is odd (not even).
To see the original proposition, suppose x² is even. If x were odd, then we just showed x² would be odd, even though it is supposed to be even; so this case is impossible. The only other possibility is that x is even.
, Latin for "by reduction toward the absurd"), it is shown that if some statement were so, a logical contradiction occurs, hence the statement must be not so. This method is perhaps the most prevalent of mathematical proofs. A famous example of proof by contradiction shows that is an irrational number
is an irrational number
:
Students can easily fall into erroneous proofs with this method. In searching for a direct proof, a mistake in reasoning will lead to false conclusions, which can often be detected as absurd, alerting the student to his or her error. But in constructing a proof by contradiction, a mistake in reasoning which implies absurd statements tends to be seen as the successful end of the proof.
, for instance, proved the existence of transcendental number
s by constructing an explicit example.
was a proof by exhaustion with 1,936 cases. This proof was controversial because the majority of the cases were checked by a computer program, not by hand. The shortest known proof of the four colour theorem today still has over 600 cases.
. This is not to be confused with an argument that a theorem is 'probably' true. The latter type of reasoning can be called a 'plausibility argument' and is not a proof; in the case of the Collatz conjecture
it is clear how far that is from a genuine proof. Probabilistic proof, like proof by construction, is one of many ways to show existence theorem
s.
between two sets is used to show that the expressions for their two sizes are equal. Alternatively, a double counting argument
provides two different expressions for the size of a single set, again showing that the two expressions are equal.
must exist (e.g. "Some X satisfies f(X)"), without explaining how such an object can be found. Often, this takes the form of a proof by contradiction in which the nonexistence of the object is proved to be impossible. In contrast, a constructive proof establishes that a particular object exists by providing a method of finding it. A famous example of a
nonconstructive proof shows that there exist two irrational number
s a and b such that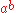 is a rational number
is a rational number
:
". The left-hand picture below is an example of a historic visual proof of the Pythagorean theorem
in the case of the (3,4,5) triangle.
to refer to proofs that make no use of complex analysis
. For some time it was thought that certain theorems, like the prime number theorem
, could only be proved using "higher" mathematics. However, over time, many of these results have been reproved using only elementary techniques.
 A particular form of proof using two parallel columns is often used in elementary geometry classes in the United States. The proof is written as a series of lines in two columns. In each line, the left-hand column contains a proposition, while the right-hand column contains a brief explanation of how the corresponding proposition in the left-hand column is either an axiom, a hypothesis, or can be logically derived from previous propositions. The left-hand column is typically headed "Statements" and the right-hand column is typically headed "Reasons".
A particular form of proof using two parallel columns is often used in elementary geometry classes in the United States. The proof is written as a series of lines in two columns. In each line, the left-hand column contains a proposition, while the right-hand column contains a brief explanation of how the corresponding proposition in the left-hand column is either an axiom, a hypothesis, or can be logically derived from previous propositions. The left-hand column is typically headed "Statements" and the right-hand column is typically headed "Reasons".
, such as involving cryptography
, chaotic series, and probabilistic or analytic number theory
. It is less commonly used to refer to a mathematical proof in the branch of mathematics known as mathematical statistics
. See also "Statistical proof using data" section below.
is an example of a computer-assisted proof. Some mathematicians are concerned that the possibility of an error in a computer program or a run-time error in its calculations calls the validity of such computer-assisted proofs into question. In practice, the chances of an error invalidating a computer-assisted proof can be reduced by incorporating redundancy and self-checks into calculations, and by developing multiple independent approaches and programs. Furthermore, although a computer might make a mistake when checking a proof, errors can never be completely ruled out in case of a human proof verifier as well, especially if the proof contains natural language and requires mathematical insight.
, which is neither provable nor refutable from the remaining axioms of Euclidean geometry.
Mathematicians have shown there are many statements that are neither provable nor disprovable in Zermelo-Fraenkel set theory with the axiom of choice (ZFC), the standard system of set theory in mathematics (assuming that ZFC is consistent); see list of statements undecidable in ZFC.
Gödel's (first) incompleteness theorem shows that many axiom systems of mathematical interest will have undecidable statements.
did not use proofs, from Euclid
to the foundational mathematics developments of the late 19th and 20th centuries, proofs were an essential part of mathematics. With the increase in computing power in the 1960s, significant work began to be done investigating mathematical objects outside of the proof-theorem framework, in experimental mathematics
. Early pioneers of these methods intended the work ultimately to be embedded in a classical proof-theorem framework, e.g. the early development of fractal geometry, which was ultimately so embedded.
.
, data analysis
, or Bayesian analysis to infer propositions regarding the probability
of data
. While using mathematical proof to establish theorems in statistics, it is usually not a mathematical proof in that the assumptions from which probability statements are derived require empirical evidence from outside mathematics to verify. In physics
, in addition to statistical methods, "statistical proof" can refer to the specialized mathematical methods of physics applied to analyze data in a particle physics
experiment
or observational study
in cosmology
. "Statistical proof" may also refer to raw data or a convincing diagram involving data, such as scatter plots, when the data or diagram is adequately convincing without further analysis.
, and may be less than one certainty
. Bayesian analysis establishes assertions as to the degree of a person's subjective belief
. Inductive logic should not be confused with mathematical induction
.
, whereby standards of mathematical proof might be applied to empirical science.
of propositions deduced in a mathematical proof, such as Descarte’s cogito
argument.
for "that which was to be demonstrated". A more common alternative is to use a square or a rectangle, such as or , known as a "tombstone
" or "halmos" after its eponym
Paul Halmos
. Often, "which was to be shown" is verbally stated when writing "QED", "", or "" in an oral presentation on a board.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a proof is a convincing demonstration (within the accepted standards of the field) that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning
Deductive reasoning
Deductive reasoning, also called deductive logic, is reasoning which constructs or evaluates deductive arguments. Deductive arguments are attempts to show that a conclusion necessarily follows from a set of premises or hypothesis...
, rather than from inductive
Inductive reasoning
Inductive reasoning, also known as induction or inductive logic, is a kind of reasoning that constructs or evaluates propositions that are abstractions of observations. It is commonly construed as a form of reasoning that makes generalizations based on individual instances...
or empirical
Empirical
The word empirical denotes information gained by means of observation or experimentation. Empirical data are data produced by an experiment or observation....
arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single exception. An unproven proposition that is believed to be true is known as a conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
.
The statement that is proved is often called a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
. Once a theorem is proved, it can be used as the basis to prove further statements. A theorem may also be referred to as a lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
, especially if it is intended for use as a stepping stone in the proof of another theorem.
Proofs employ logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
but usually include some amount of natural language
Natural language
In the philosophy of language, a natural language is any language which arises in an unpremeditated fashion as the result of the innate facility for language possessed by the human intellect. A natural language is typically used for communication, and may be spoken, signed, or written...
which usually admits some ambiguity. In fact, the vast majority of proofs in written mathematics can be considered as applications of rigorous informal logic
Informal logic
Informal logic, intuitively, refers to the principles of logic and logical thought outside of a formal setting. However, perhaps because of the informal in the title, the precise definition of informal logic is matters of some dispute. Ralph H. Johnson and J...
. Purely formal proof
Formal proof
A formal proof or derivation is a finite sequence of sentences each of which is an axiom or follows from the preceding sentences in the sequence by a rule of inference. The last sentence in the sequence is a theorem of a formal system...
s, written in symbolic language instead of natural language, are considered in proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
. The distinction between formal and informal proofs has led to much examination of current and historical mathematical practice
Mathematical practice
Mathematical practice is used to distinguish the working practices of professional mathematicians from the end result of proven and published theorems.-Quasi-empiricism:This distinction is...
, quasi-empiricism in mathematics
Quasi-empiricism in mathematics
Quasi-empiricism in mathematics is the attempt in the philosophy of mathematics to direct philosophers' attention to mathematical practice, in particular, relations with physics, social sciences, and computational mathematics, rather than solely to issues in the foundations of mathematics...
, and so-called folk mathematics (in both senses of that term). The philosophy of mathematics
Philosophy of mathematics
The philosophy of mathematics is the branch of philosophy that studies the philosophical assumptions, foundations, and implications of mathematics. The aim of the philosophy of mathematics is to provide an account of the nature and methodology of mathematics and to understand the place of...
is concerned with the role of language and logic in proofs, and mathematics as a language
Mathematics as a language
The language of mathematics is the system used by mathematicians to communicate mathematical ideas among themselves. This language consists of a substrate of some natural language using technical terms and grammatical conventions that are peculiar to mathematical discourse , supplemented by a...
.
History and etymology
The word Proof comes from the Latin probare meaning "to test". Related modern words are the English "probe", "proboscis”, "probation", and "probability", the Spanish "probar" (to smell or taste, or (lesser use) touch or test), Italian "provare" (to try), and the German "probieren" (to try). The early use of "probity" was in the presentation of legal evidence. A person of authority, such as a nobleman, was said to have probity, whereby the evidence was by his relative authority, which outweighed empirical testimony.Plausibility arguments using heuristic devices such as pictures and analogies preceded strict mathematical proof. It is probable that the idea of demonstrating a conclusion first arose in connection with geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, which originally meant the same as "land measurement". The development of mathematical proof is primarily the product of ancient Greek mathematics
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
, and one of its greatest achievements. Thales
Thales
Thales of Miletus was a pre-Socratic Greek philosopher from Miletus in Asia Minor, and one of the Seven Sages of Greece. Many, most notably Aristotle, regard him as the first philosopher in the Greek tradition...
(624–546 BCE) proved some theorems in geometry. Eudoxus
Eudoxus of Cnidus
Eudoxus of Cnidus was a Greek astronomer, mathematician, scholar and student of Plato. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus's poem on astronomy...
(408–355 BCE) and Theaetetus
Theaetetus (mathematician)
Theaetetus, Theaitētos, of Athens, possibly son of Euphronius, of the Athenian deme Sunium, was a classical Greek mathematician...
(417–369 BCE) formulated theorems but did not prove them. Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
(384–322 BCE) said definitions should describe the concept being defined in terms of other concepts already known. Mathematical proofs were revolutionized by Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
(300 BCE), who introduced the axiomatic method still in use today, starting with undefined terms and axioms (propositions regarding the undefined terms assumed to be self-evidently true from the Greek “axios” meaning “something worthy”), and used these to prove theorems using deductive logic. His book, the Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
, was read by anyone who was considered educated in the West until the middle of the 20th century. In addition to the familiar theorems of geometry, such as the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, the Elements includes a proof that the square root of two is irrational and that there are infinitely many prime numbers.
Further advances took place in medieval Islamic mathematics. While earlier Greek proofs were largely geometric demonstrations, the development of arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
and algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
by Islamic mathematicians allowed more general proofs that no longer depended on geometry. In the 10th century CE, the Iraqi
Iraqi people
The Iraqi people or Mesopotamian people are natives or inhabitants of the country of Iraq, known since antiquity as Mesopotamia , with a large diaspora throughout the Arab World, Europe, the Americas, and...
mathematician Al-Hashimi provided general proofs for numbers (rather than geometric demonstrations) as he considered multiplication, division, etc. for ”lines.” He used this method to provide a proof of the existence of irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s. An inductive proof
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
for arithmetic sequences
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
was introduced in the Al-Fakhri (1000) by Al-Karaji
Al-Karaji
' was a 10th century Persian Muslim mathematician and engineer. His three major works are Al-Badi' fi'l-hisab , Al-Fakhri fi'l-jabr wa'l-muqabala , and Al-Kafi fi'l-hisab .Because al-Karaji's original works in Arabic are lost, it is not...
, who used it to prove the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
and properties of Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
. Alhazen also developed the method of proof by contradiction, as the first attempt at proving the Euclidean
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
parallel postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
.
Modern proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
treats proofs as inductively defined data structures. There is no longer an assumption that axioms are "true" in any sense; this allows for parallel mathematical theories built on alternate sets of axioms (see Axiomatic set theory and Non-Euclidean geometry
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
for examples).
Nature and purpose
There are two different conceptions of mathematical proof. The first is an informal proof, a rigorous natural-language expression that is intended to convince the audience of the truth of a theorem. Because of their use of natural language, the standards of rigor for informal proofs will depend on the audience of the proof. In order to be considered a proof, however, the argument must be rigorous enough; a vague or incomplete argument is not a proof. Informal proofs are the type of proof typically encountered in published mathematics. They are sometimes called "formal proofs" because of their rigor, but logicians use the term "formal proof" to refer to a different type of proof entirely.In logic, a formal proof
Formal proof
A formal proof or derivation is a finite sequence of sentences each of which is an axiom or follows from the preceding sentences in the sequence by a rule of inference. The last sentence in the sequence is a theorem of a formal system...
is not written in a natural language, but instead uses a formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
consisting of certain strings of symbols from a fixed alphabet. This allows the definition of a formal proof to be precisely specified without any ambiguity. The field of proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
studies formal proofs and their properties. Although each informal proof can, in theory, be converted into a formal proof, this is rarely done in practice. The study of formal proofs is used to determine properties of in general, and to show that certain undecidable statement
Independence (mathematical logic)
In mathematical logic, independence refers to the unprovability of a sentence from other sentences.A sentence σ is independent of a given first-order theory T if T neither proves nor refutes σ; that is, it is impossible to prove σ from T, and it is also impossible to prove from T that...
s are not provable.
A classic question in philosophy asks whether mathematical proofs are analytic or synthetic. Kant, who introduced the analytic-synthetic distinction, believed mathematical proofs are synthetic.
Proofs may be viewed as aesthetic objects, admired for their mathematical beauty
Mathematical beauty
Many mathematicians derive aesthetic pleasure from their work, and from mathematics in general. They express this pleasure by describing mathematics as beautiful. Sometimes mathematicians describe mathematics as an art form or, at a minimum, as a creative activity...
. The mathematician Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
was known for describing proofs he found particularly elegant as coming from "The Book", a hypothetical tome containing the most beautiful method(s) of proving each theorem. The book Proofs from THE BOOK
Proofs from THE BOOK
Proofs from THE BOOK is a book of mathematical proofs by Martin Aigner and Günter M. Ziegler. The book is dedicated to the mathematician Paul Erdős, who often referred to "The Book" in which God keeps the most elegant proof of each mathematical theorem...
, published in 2003, is devoted to presenting 32 proofs its editors find particularly pleasing.
Direct proof
In direct proof, the conclusion is established by logically combining the axioms, definitions, and earlier theorems. For example, direct proof can be used to establish that the sum of two evenEven and odd numbers
In mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s is always even:
- Consider two even integers x and y. Since they are even, they can be written as x=2a and y=2b respectively for integers a and b. Then the sum
 . From this it is clear x+y has 2 as a factor and therefore is even, so the sum of any two even integers is even.
. From this it is clear x+y has 2 as a factor and therefore is even, so the sum of any two even integers is even.
This proof uses definition of even integers, as well as distribution law
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
.
Proof by mathematical induction
In proof by mathematical induction, first a "base case" is proved, and then an "induction rule" is used to prove a (often infinite) series of other cases. Since the base case is true, the infinity of other cases must also be true, even if all of them cannot be proved directly because of their infinite number. A subset of induction is infinite descentInfinite descent
In mathematics, a proof by infinite descent is a particular kind of proof by contradiction which relies on the fact that the natural numbers are well ordered. One typical application is to show that a given equation has no solutions. Assuming a solution exists, one shows that another exists, that...
. Infinite descent can be used to prove the irrationality of the square root of two.
The principle of mathematical induction states that:
Let N = { 1, 2, 3, 4, ... } be the set of natural numbers and P(n) be a mathematical statement involving the natural number n belonging to N such that
- (i) P(1) is true, i.e., P(n) is true for n = 1
- (ii) P(n + 1) is true whenever P(n) is true, i.e., P(n) is true implies that P(n + 1) is true.
Then P(n) is true for all natural numbers n.
Mathematicians often use the term "proof by induction" as shorthand for a proof by mathematical induction. However, the term "proof by induction" may also be used in logic to mean an argument that uses inductive reasoning
Inductive reasoning
Inductive reasoning, also known as induction or inductive logic, is a kind of reasoning that constructs or evaluates propositions that are abstractions of observations. It is commonly construed as a form of reasoning that makes generalizations based on individual instances...
.
Proof by transposition
Proof by transposition or proof by contrapositiveProof by contrapositive
In logic, the contrapositive of a conditional statement of the form "if A then B" is formed by negating both terms and reversing the direction of inference...
establishes the conclusion "if p then q" by proving the equivalent contrapositive statement "if not q then not p".
Example:
- Proposition: If x² is even then x is even.
- Contrapositive proof:
If x is odd (not even) then x = 2k + 1 for an integer k.
Thus x² = (2k + 1)² = 4k² + 4k + 1 = 2(2k² + 2k) + 1, where (2k² + 2k) is an integer.
Therefore x² is odd (not even).
To see the original proposition, suppose x² is even. If x were odd, then we just showed x² would be odd, even though it is supposed to be even; so this case is impossible. The only other possibility is that x is even.
Proof by contradiction
In proof by contradiction (also known as reductio ad absurdumReductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
, Latin for "by reduction toward the absurd"), it is shown that if some statement were so, a logical contradiction occurs, hence the statement must be not so. This method is perhaps the most prevalent of mathematical proofs. A famous example of proof by contradiction shows that
 is an irrational number
is an irrational numberIrrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
:
- Suppose that
 were a rational number, so by definition
were a rational number, so by definition 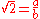 where a and b are non-zero integers with no common factorCoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
where a and b are non-zero integers with no common factorCoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
. Thus, . Squaring both sides yields 2b2 = a2. Since 2 divides the left hand side, 2 must also divide the right hand side (as they are equal and both integers). So a2 is even, which implies that a must also be even. So we can write a = 2c, where c is also an integer. Substitution into the original equation yields 2b2 = (2c)2 = 4c2. Dividing both sides by 2 yields b2 = 2c2. But then, by the same argument as before, 2 divides b2, so b must be even. However, if a and b are both even, they share a factor, namely 2. This contradicts our assumption, so we are forced to conclude that
. Squaring both sides yields 2b2 = a2. Since 2 divides the left hand side, 2 must also divide the right hand side (as they are equal and both integers). So a2 is even, which implies that a must also be even. So we can write a = 2c, where c is also an integer. Substitution into the original equation yields 2b2 = (2c)2 = 4c2. Dividing both sides by 2 yields b2 = 2c2. But then, by the same argument as before, 2 divides b2, so b must be even. However, if a and b are both even, they share a factor, namely 2. This contradicts our assumption, so we are forced to conclude that  is an irrational number.
is an irrational number.
Students can easily fall into erroneous proofs with this method. In searching for a direct proof, a mistake in reasoning will lead to false conclusions, which can often be detected as absurd, alerting the student to his or her error. But in constructing a proof by contradiction, a mistake in reasoning which implies absurd statements tends to be seen as the successful end of the proof.
Proof by construction
Proof by construction, or proof by example, is the construction of a concrete example with a property to show that something having that property exists. Joseph LiouvilleJoseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
, for instance, proved the existence of transcendental number
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
s by constructing an explicit example.
Proof by exhaustion
In proof by exhaustion, the conclusion is established by dividing it into a finite number of cases and proving each one separately. The number of cases sometimes can become very large. For example, the first proof of the four color theoremFour color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
was a proof by exhaustion with 1,936 cases. This proof was controversial because the majority of the cases were checked by a computer program, not by hand. The shortest known proof of the four colour theorem today still has over 600 cases.
Probabilistic proof
A probabilistic proof is one in which an example is shown to exist, with certainty, by using methods of probability theoryProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. This is not to be confused with an argument that a theorem is 'probably' true. The latter type of reasoning can be called a 'plausibility argument' and is not a proof; in the case of the Collatz conjecture
Collatz conjecture
The Collatz conjecture is a conjecture in mathematics named after Lothar Collatz, who first proposed it in 1937. The conjecture is also known as the 3n + 1 conjecture, the Ulam conjecture , Kakutani's problem , the Thwaites conjecture , Hasse's algorithm The Collatz conjecture is a...
it is clear how far that is from a genuine proof. Probabilistic proof, like proof by construction, is one of many ways to show existence theorem
Existence theorem
In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...
s.
Combinatorial proof
A combinatorial proof establishes the equivalence of different expressions by showing that they count the same object in different ways. Often a bijectionBijective proof
In combinatorics, bijective proof is a proof technique that finds a bijective function f : A → B between two sets A and B, thus proving that they have the same number of elements, |A| = |B|. One place the technique is useful is where we wish to know the size of A, but can find no direct way of...
between two sets is used to show that the expressions for their two sizes are equal. Alternatively, a double counting argument
Double counting (proof technique)
In combinatorics, double counting, also called counting in two ways, is a combinatorial proof technique for showing that two expressions are equal by demonstrating that they are two ways of counting the size of one set...
provides two different expressions for the size of a single set, again showing that the two expressions are equal.
Nonconstructive proof
A nonconstructive proof establishes that a certain mathematical objectMathematical object
In mathematics and the philosophy of mathematics, a mathematical object is an abstract object arising in mathematics.Commonly encountered mathematical objects include numbers, permutations, partitions, matrices, sets, functions, and relations...
must exist (e.g. "Some X satisfies f(X)"), without explaining how such an object can be found. Often, this takes the form of a proof by contradiction in which the nonexistence of the object is proved to be impossible. In contrast, a constructive proof establishes that a particular object exists by providing a method of finding it. A famous example of a
nonconstructive proof shows that there exist two irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s a and b such that
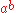 is a rational number
is a rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
:
- Either
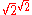 is a rational number and we are done (take
is a rational number and we are done (take 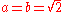 ), or
), or 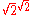 is irrational so we can write
is irrational so we can write 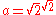 and
and 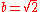 . This then gives
. This then gives  , which is thus a rational of the form
, which is thus a rational of the form 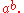
Visual proof
Although not a formal proof, a visual demonstration of a mathematical theorem is sometimes called a "proof without wordsProof without words
In mathematics, a proof without words is a proof of an identity or mathematical statement which can be demonstrated as self-evident by a diagram without any accompanying explanatory text. Such proofs can be considered more elegant than more formal and mathematically rigorous proofs due to their...
". The left-hand picture below is an example of a historic visual proof of the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
in the case of the (3,4,5) triangle.
Elementary proof
An elementary proof is a proof which only uses basic techniques. More specifically, the term is used in number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
to refer to proofs that make no use of complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
. For some time it was thought that certain theorems, like the prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
, could only be proved using "higher" mathematics. However, over time, many of these results have been reproved using only elementary techniques.
Two-column proof

Statistical proofs in pure mathematics
The expression "statistical proof" may be used technically or colloquially in areas of pure mathematicsPure mathematics
Broadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
, such as involving cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, chaotic series, and probabilistic or analytic number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. It is less commonly used to refer to a mathematical proof in the branch of mathematics known as mathematical statistics
Mathematical statistics
Mathematical statistics is the study of statistics from a mathematical standpoint, using probability theory as well as other branches of mathematics such as linear algebra and analysis...
. See also "Statistical proof using data" section below.
Computer-assisted proofs
Until the twentieth century it was assumed that any proof could, in principle, be checked by a competent mathematician to confirm its validity. However, computers are now used both to prove theorems and to carry out calculations that are too long for any human or team of humans to check; the first proof of the four color theoremFour color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
is an example of a computer-assisted proof. Some mathematicians are concerned that the possibility of an error in a computer program or a run-time error in its calculations calls the validity of such computer-assisted proofs into question. In practice, the chances of an error invalidating a computer-assisted proof can be reduced by incorporating redundancy and self-checks into calculations, and by developing multiple independent approaches and programs. Furthermore, although a computer might make a mistake when checking a proof, errors can never be completely ruled out in case of a human proof verifier as well, especially if the proof contains natural language and requires mathematical insight.
Undecidable statements
A statement that is neither provable nor disprovable from a set of axioms is called undecidable (from those axioms). One example is the parallel postulateParallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
, which is neither provable nor refutable from the remaining axioms of Euclidean geometry.
Mathematicians have shown there are many statements that are neither provable nor disprovable in Zermelo-Fraenkel set theory with the axiom of choice (ZFC), the standard system of set theory in mathematics (assuming that ZFC is consistent); see list of statements undecidable in ZFC.
Gödel's (first) incompleteness theorem shows that many axiom systems of mathematical interest will have undecidable statements.
Heuristic mathematics and experimental mathematics
While early mathematicians such as Eudoxus of CnidusEudoxus of Cnidus
Eudoxus of Cnidus was a Greek astronomer, mathematician, scholar and student of Plato. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus's poem on astronomy...
did not use proofs, from Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
to the foundational mathematics developments of the late 19th and 20th centuries, proofs were an essential part of mathematics. With the increase in computing power in the 1960s, significant work began to be done investigating mathematical objects outside of the proof-theorem framework, in experimental mathematics
Experimental mathematics
Experimental mathematics is an approach to mathematics in which numerical computation is used to investigate mathematical objects and identify properties and patterns...
. Early pioneers of these methods intended the work ultimately to be embedded in a classical proof-theorem framework, e.g. the early development of fractal geometry, which was ultimately so embedded.
Colloquial use of "mathematical proof"
The expression "mathematical proof" is used by lay people to refer to using mathematical methods or arguing with mathematical objects, such as numbers, to demonstrate something about everyday life, or when data used in an argument are numbers. It is sometime also used to mean a "statistical proof" (below), especially when used to argue from dataData
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
.
Statistical proof using data
"Statistical proof" from data refers to the application of statisticsStatistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, data analysis
Data analysis
Analysis of data is a process of inspecting, cleaning, transforming, and modeling data with the goal of highlighting useful information, suggesting conclusions, and supporting decision making...
, or Bayesian analysis to infer propositions regarding the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of data
Data
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
. While using mathematical proof to establish theorems in statistics, it is usually not a mathematical proof in that the assumptions from which probability statements are derived require empirical evidence from outside mathematics to verify. In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, in addition to statistical methods, "statistical proof" can refer to the specialized mathematical methods of physics applied to analyze data in a particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
experiment
Experiment
An experiment is a methodical procedure carried out with the goal of verifying, falsifying, or establishing the validity of a hypothesis. Experiments vary greatly in their goal and scale, but always rely on repeatable procedure and logical analysis of the results...
or observational study
Observational study
In epidemiology and statistics, an observational study draws inferences about the possible effect of a treatment on subjects, where the assignment of subjects into a treated group versus a control group is outside the control of the investigator...
in cosmology
Cosmology
Cosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...
. "Statistical proof" may also refer to raw data or a convincing diagram involving data, such as scatter plots, when the data or diagram is adequately convincing without further analysis.
Inductive logic proofs and Bayesian analysis
Proofs using inductive logic, while considered mathematical in nature, seek to establish propositions with a degree of certainty, which acts in a similar manner to probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, and may be less than one certainty
Certainty
Certainty can be defined as either:# perfect knowledge that has total security from error, or# the mental state of being without doubtObjectively defined, certainty is total continuity and validity of all foundational inquiry, to the highest degree of precision. Something is certain only if no...
. Bayesian analysis establishes assertions as to the degree of a person's subjective belief
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
. Inductive logic should not be confused with mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
.
Proofs as mental objects
Psychologism views mathematical proofs as psychological or mental objects. Mathematician philosophers, such as Leibniz, Frege, and Carnap, have attempted to develop a semantics for what they considered to be the language of thoughtLanguage of thought
In philosophy of mind, the language of thought hypothesis put forward by American philosopher Jerry Fodor describes thoughts as represented in a "language" that allows complex thoughts to be built up by combining simpler thoughts in various ways...
, whereby standards of mathematical proof might be applied to empirical science.
Influence of mathematical proof methods outside mathematics
Philosopher-mathematicians such as Schopenhauer have attempted to formulate philosophical arguments in an axiomatic manner, whereby mathematical proof standards could be applied to argumentation in general philosophy. Other mathematician-philosophers have tried to use standards of mathematical proof and reason, without empiricism, to arrive at statements outside of mathematics, but having the certaintyCertainty
Certainty can be defined as either:# perfect knowledge that has total security from error, or# the mental state of being without doubtObjectively defined, certainty is total continuity and validity of all foundational inquiry, to the highest degree of precision. Something is certain only if no...
of propositions deduced in a mathematical proof, such as Descarte’s cogito
Cogito ergo sum
is a philosophical Latin statement proposed by . The simple meaning of the phrase is that someone wondering whether or not they exist is, in and of itself, proof that something, an "I", exists to do the thinking — However this "I" is not the more or less permanent person we call "I"...
argument.
Ending a proof
Sometimes, the abbreviation "Q.E.D." is written to indicate the end of a proof. This abbreviation stands for "Quod Erat Demonstrandum", which is LatinLatin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
for "that which was to be demonstrated". A more common alternative is to use a square or a rectangle, such as or , known as a "tombstone
Tombstone (typography)
The tombstone, halmos, or end of proof mark "" is used in mathematics to denote the end of a proof, in place of the traditional abbreviation "QED" for the Latin phrase "quod erat demonstrandum" ....
" or "halmos" after its eponym
Eponym
An eponym is the name of a person or thing, whether real or fictitious, after which a particular place, tribe, era, discovery, or other item is named or thought to be named...
Paul Halmos
Paul Halmos
Paul Richard Halmos was a Hungarian-born American mathematician who made fundamental advances in the areas of probability theory, statistics, operator theory, ergodic theory, and functional analysis . He was also recognized as a great mathematical expositor.-Career:Halmos obtained his B.A...
. Often, "which was to be shown" is verbally stated when writing "QED", "", or "" in an oral presentation on a board.
See also
- Automated theorem provingAutomated theorem provingAutomated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
- Invalid proofInvalid proofIn mathematics, certain kinds of mistakes in proof, calculation, or derivation are often exhibited, and sometimes collected, as illustrations of the concept of mathematical fallacy...
- List of incomplete proofs
- List of long proofs
- List of mathematical proofs
- Nonconstructive proof
- Proof by intimidationProof by intimidationProof by intimidation is a jocular term used mainly in mathematics to refer to a style of presenting a purported mathematical proof by giving an argument loaded with jargon and appeal to obscure results, so that the audience is simply obliged to accept it, lest they have to admit their ignorance...
- What the Tortoise Said to AchillesWhat the Tortoise Said to Achilles"What the Tortoise Said to Achilles", written by Lewis Carroll in 1895 for the philosophical journal Mind, is a brief dialogue which problematises the foundations of logic. The title alludes to one of Zeno's paradoxes of motion, in which Achilles could never overtake the tortoise in a race...
(Lewis CarrollLewis CarrollCharles Lutwidge Dodgson , better known by the pseudonym Lewis Carroll , was an English author, mathematician, logician, Anglican deacon and photographer. His most famous writings are Alice's Adventures in Wonderland and its sequel Through the Looking-Glass, as well as the poems "The Hunting of the...
's reasoning for the paradoxical invalidity of deductive proofs)
External links
- What are mathematical proofs and why they are important?
- 2πix.com: Logic Part of a series of articles covering mathematics and logic.
- How To Write Proofs by Larry W. Cusick
- How to Write a Proof by Leslie LamportLeslie LamportLeslie Lamport is an American computer scientist. A graduate of the Bronx High School of Science, he received a B.S. in mathematics from the Massachusetts Institute of Technology in 1960, and M.A. and Ph.D. degrees in mathematics from Brandeis University, respectively in 1963 and 1972...
, and the motivation of proposing such a hierarchical proof style. - Proofs in Mathematics: Simple, Charming and Fallacious
- The Seventeen Provers of the World, ed. by Freek Wiedijk, foreword by Dana S. Scott, Lecture Notes in Computer Science 3600, Springer, 2006, ISBN 3-540-30704-4. Contains formalized versions of the proof that
 is irrational in several automated proof systems.
is irrational in several automated proof systems. - What is Proof? Thoughts on proofs and proving.
- ProofWiki.org An online compendium of mathematical proofs.
- planetmath.org A wiki style encyclopedia of proofs
- A lesson about proofs, in a course from Wikiversity
- The role and function of proof by Michael de Villiers
- Developing understanding of different roles of proof by Michael de Villiers

