
Kepler conjecture
Encyclopedia

Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
, is a mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
about sphere packing
Sphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
in three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. It says that no arrangement of equally sized sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s filling space has a greater average density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
than that of the cubic close packing (face-centered cubic) and hexagonal close packing arrangements. The density of these arrangements is slightly greater than 74%.
In 1998 Thomas Hales
Thomas Callister Hales
Thomas Callister Hales is an American mathematician. He is known for his 1998 computer-aided proof of the Kepler conjecture, a centuries-old problem in discrete geometry which states that the most space-efficient way to pack spheres is in a pyramid shape...
, following an approach suggested by , announced that he had a proof of the Kepler conjecture. Hales' proof is a proof by exhaustion
Proof by exhaustion
Proof by exhaustion, also known as proof by cases, perfect induction, or the brute force method, is a method of mathematical proof in which the statement to be proved is split into a finite number of cases and each case is checked to see if the proposition in question holds...
involving the checking of many individual cases using complex computer calculations. Referees have said that they are "99% certain" of the correctness of Hales' proof, so the Kepler conjecture is now very close to being accepted as a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
.
Background
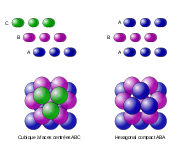
Experiment shows that dropping the spheres in randomly will achieve a density of around 65%. However, a higher density can be achieved by carefully arranging the spheres as follows. Start with a layer of spheres in a hexagonal lattice, then put the next layer of spheres in the lowest points you can find above the first layer, and so on – this is just the way you see oranges stacked in a shop. At each step there are two choices of where to put the next layer, so this natural method of stacking the spheres creates an uncountably infinite number of equally dense packings, the best known of which are called cubic close packing and hexagonal close packing. Each of these arrangements has an average density of
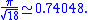
The Kepler conjecture says that this is the best that can be done—no other arrangement of spheres has a higher average density.
Origins
The conjecture was first stated by in his paper 'On the six-cornered snowflake'. He had started to study arrangements of spheres as a result of his correspondence with the English mathematician and astronomer Thomas HarriotThomas Harriot
Thomas Harriot was an English astronomer, mathematician, ethnographer, and translator. Some sources give his surname as Harriott or Hariot or Heriot. He is sometimes credited with the introduction of the potato to Great Britain and Ireland...
in 1606. Harriot was a friend and assistant of Sir Walter Raleigh, who had set Harriot the problem of determining how best to stack cannon balls on the decks of his ships. Harriot published a study of various stacking patterns in 1591, and went on to develop an early version of atomic theory
Atomic theory
In chemistry and physics, atomic theory is a theory of the nature of matter, which states that matter is composed of discrete units called atoms, as opposed to the obsolete notion that matter could be divided into any arbitrarily small quantity...
.
Nineteenth century
Kepler did not have a proof of the conjecture, and the next step was taken by , who proved that the Kepler conjecture is true if the spheres have to be arranged in a regular latticeLattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
.
This meant that any packing arrangement that disproved the Kepler conjecture would have to be an irregular one. But eliminating all possible irregular arrangements is very difficult, and this is what made the Kepler conjecture so hard to prove. In fact, there are irregular arrangements that are denser than the cubic close packing arrangement over a small enough volume, but any attempt to extend these arrangements to fill a larger volume always reduces their density.
After Gauss, no further progress was made towards proving the Kepler conjecture in the nineteenth century. In 1900 David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
included it in his list of twenty three unsolved problems of mathematics
Hilbert's problems
Hilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
—it forms part of Hilbert's eighteenth problem
Hilbert's eighteenth problem
Hilbert's eighteenth problem is one of the 23 Hilbert problems set out in a celebrated list compiled in 1900 by mathematician David Hilbert. It asks three separate questions about lattices and sphere packing in Euclidean space....
.
Twentieth century
The next step toward a solution was taken by Hungarian mathematician László Fejes TóthLászló Fejes Tóth
László Fejes Tóth was a Hungarian mathematician who specialised in geometry. He proved that a honeycomb pattern is the most efficient way to pack centrally symmetric convex sets on the Euclidean plane . He also investigated packings on the sphere...
. showed that the problem of determining the maximum density of all arrangements (regular and irregular) could be reduced to a finite (but very large) number of calculations. This meant that a proof by exhaustion was, in principle, possible. As Fejes Tóth realised, a fast enough computer could turn this theoretical result into a practical approach to the problem.
Meanwhile, attempts were made to find an upper bound for the maximum density of any possible arrangement of spheres. English mathematician Claude Ambrose established an upper bound value of about 78%, and subsequent efforts by other mathematicians reduced this value slightly, but this was still much larger than the cubic close packing density of about 74%.
claimed to prove the Kepler conjecture using geometric methods. However Gábor Fejes Tóth (the son of László Fejes Tóth) stated in his review of the paper "As far as details are concerned, my opinion is that many of the key statements have no acceptable proofs."
gave a detailed criticism of Hsiang's work, to which responded. The current consensus is that Hsiang's proof is incomplete.
Hales' proof
Following the approach suggested by , Thomas Hales, then at the University of MichiganUniversity of Michigan
The University of Michigan is a public research university located in Ann Arbor, Michigan in the United States. It is the state's oldest university and the flagship campus of the University of Michigan...
, determined that the maximum density of all arrangements could be found by minimizing a function with 150 variables. In 1992, assisted by his graduate student Samuel Ferguson, he embarked on a research program to systematically apply linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
methods to find a lower bound on the value of this function for each one of a set of over 5,000 different configurations of spheres. If a lower bound (for the function value) could be found for every one of these configurations that was greater than the value of the function for the cubic close packing arrangement, then the Kepler conjecture would be proved. To find lower bounds for all cases involved solving around 100,000 linear programming problems.
When presenting the progress of his project in 1996, Hales said that the end was in sight, but it might take "a year or two" to complete. In August 1998 Hales announced that the proof was complete. At that stage it consisted of 250 pages of notes and 3 gigabyte
Gigabyte
The gigabyte is a multiple of the unit byte for digital information storage. The prefix giga means 109 in the International System of Units , therefore 1 gigabyte is...
s of computer programs, data and results.
Despite the unusual nature of the proof, the editors of the Annals of Mathematics
Annals of Mathematics
The Annals of Mathematics is a bimonthly mathematical journal published by Princeton University and the Institute for Advanced Study. It ranks amongst the most prestigious mathematics journals in the world by criteria such as impact factor.-History:The journal began as The Analyst in 1874 and was...
agreed to publish it, provided it was accepted by a panel of twelve referees. In 2003, after four years of work, the head of the referee's panel Gábor Fejes Tóth (son of László Fejes Tóth
László Fejes Tóth
László Fejes Tóth was a Hungarian mathematician who specialised in geometry. He proved that a honeycomb pattern is the most efficient way to pack centrally symmetric convex sets on the Euclidean plane . He also investigated packings on the sphere...
) reported that the panel were "99% certain" of the correctness of the proof, but they could not certify the correctness of all of the computer calculations.
published a 100-page paper describing the non-computer part of his proof in detail.
and several subsequent papers described the computational portions. Hales and Ferguson received the Fulkerson Prize for outstanding papers in the area of discrete mathematics
Fulkerson Prize
The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Programming Society and the American Mathematical Society . Up to three awards of $1500 each are presented at each International Symposium of the MPS...
for 2009.
A formal proof
In January 2003, Hales announced the start of a collaborative project to produce a complete formal proof of the Kepler conjecture. The aim is to remove any remaining uncertainty about the validity of the proof by creating a formal proof that can be verified by automated proof checking software such as HOLHOL theorem prover
HOL denotes a family of interactive theorem proving systems sharingsimilar logics and implementation strategies....
. This project is called Project FlysPecK – the F, P and K standing for Formal Proof of Kepler. Hales estimates that producing a complete formal proof will take around 20 years of work.
Related problems
ThueAxel Thue
Axel Thue was a Norwegian mathematician, known for highly original work in diophantine approximation, and combinatorics....
's theorem: The regular hexagonal packing is the densest sphere packing in the plane. (1890)
- The 2-dimensional analog of the Kepler conjecture; the proof is elementary. Henk and Ziegler attribute this result to Lagrange, in 1773 (see references, pag. 770).
The hexagonal honeycomb conjecture: The most efficient partition of the plane into equal areas is the regular hexagonal tiling. Hales' proof (1999).
- Related to Thue's theorem.
The dodecahedron conjecture: The volume of the Voronoi polyhedron of a sphere in a packing of equal spheres is at least the volume of a regular dodecahedron with inradius 1. McLaughlin's proof, for which he received the 1999 Morgan Prize
Frank and Brennie Morgan Prize for Outstanding Research in Mathematics by an Undergraduate Student
The Morgan Prize is an annual award given to an undergraduate student in the US, Canada, or Mexico who demonstrates superior mathematics research. The $1,000 award, endowed by Mrs. Frank Morgan of Allentown, Pennsylvania, was founded in 1995...
.
- A related problem, whose proof uses similar techniques to Hales' proof of the Kepler conjecture. Conjecture by L. Fejes Tóth in the 1950s.
The Kelvin problem: What is the most efficient foam
Foam
-Definition:A foam is a substance that is formed by trapping gas in a liquid or solid in a divided form, i.e. by forming gas regions inside liquid regions, leading to different kinds of dispersed media...
in 3 dimensions? This was conjectured to be solved by the Kelvin structure, and this was widely believed for over 100 years, until disproved by the discovery of the Weaire–Phelan structure. The surprising discovery of the Weaire–Phelan structure and disproof of the Kelvin conjecture is one reason for the caution in accepting Hales' proof of the Kepler conjecture.
Sphere packing
Sphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
in higher dimensions: The optimal sphere packing question in dimensions bigger than 3 is still open.

