
Nth root
Encyclopedia
In mathematics
, the nth root of a number
x is a number r which, when raised to the power of n, equals x
where n is the degree of the root. A root of degree 2 is usually called a square root
and a root of degree 3, a cube root.
For example:
A number may have many roots of degree n and the roots are not necessarily real numbers.
Roots are usually written using the radical symbol , with
, with  denoting the square root,
denoting the square root, 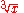 denoting the cube root,
denoting the cube root,  denoting the fourth root, and so on. In the expression
denoting the fourth root, and so on. In the expression  , n is called the index,
, n is called the index,  is the radical sign, and x is called the radicand. When a number is presented under the radical symbol, it must return only one result like a function
is the radical sign, and x is called the radicand. When a number is presented under the radical symbol, it must return only one result like a function
, so a non-negative real root, called the principal nth root, is preferred rather than others. An unresolved root, especially one using the radical symbol, is often referred to as a surd or a radical. Any expression containing a radical, whether it is a square root, a cube root, or a higher root, is called a radical expression.
In calculus
, roots are treated as special cases of exponentiation, where the exponent is a fraction
:
Roots are particularly important in the theory of infinite series
; the root test determines the radius of convergence
of a power series. Nth roots can also be defined for complex number
s, and the complex roots of 1 (the roots of unity
) play an important role in higher mathematics. Galois theory
can be used to determine which algebraic number
s can be expressed using roots, and to prove the Abel-Ruffini theorem, which states that a general polynomial
equation of degree five or higher cannot be solved using roots alone; this result is also known as "the insolubility of the quintic".
(1421–1486). Legend has it that it was taken from the Arabic letter ج, which is the first letter in the word Jadhir "root" in Arabic. (The dh in Jadhir is a voiced interdental fricative, like the th in English the.) Many scholars, however, including Leonhard Euler
believe it originates from the letter
r, the first letter of radix
"root" in Latin
word referring to the same mathematical operation
. The symbol was first seen in print without the vinculum (the horizontal "bar" over the numbers inside the radical symbol) in the year 1525 in Die Coss by Christoff Rudolff, a German mathematician.
The term surd traces back to al-Khwārizmī (c. 825), who referred to rational and irrational numbers as audible and inaudible, respectively. This later led to the Arabic asamm (deaf, dumb) for irrational number being translated as surdus (deaf or mute) into Latin. Gherardo of Cremona (c. 1150), Fibonacci (1202) and then Robert Recorde (1551) all used the term to refer to unresolved irrational roots.

Every positive real number
x has a single positive nth root, which is written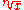 . For n equal to 2 this is called the square root and the n is omitted. The nth root can also be represented using exponentiation
. For n equal to 2 this is called the square root and the n is omitted. The nth root can also be represented using exponentiation
as x1/n.
For even values of n, positive numbers also have a negative nth root, while negative numbers do not have a real nth root. For odd values of n, every negative number x has a real negative nth root. For example, −2 has a real 5th root,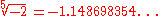 but −2 does not have any real 6th roots.
but −2 does not have any real 6th roots.
Every non-zero number x, real or complex
, has n different complex number nth roots including any positive or negative roots, see complex roots below. The nth root of 0 is 0.
For most numbers, an nth root is irrational
. For example,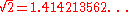
All nth roots of integers, or in fact of any algebraic number
, are algebraic.
For the extension of powers and roots to indices that are not positive integers, see exponentiation
.
The character codes for the radical symbols are

Every positive real number has two square roots, one positive and one negative. For example, the two square roots of 25 are 5 and −5. The positive square root is also known as the principal square root, and is denoted with a radical sign:
Since the square of every real number is a positive real number, negative numbers do not have real square roots. However, every negative number has two imaginary
square roots. For example, the square roots of −25 are 5i and −5i, where i
represents a square root of −1.

Every real number x has exactly one real cube root, written . For example,
. For example,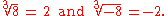
Every real number has two additional complex
cube roots (see complex roots below).
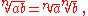

Using the exponent form as in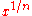 normally makes it easier to cancel out powers and roots.
normally makes it easier to cancel out powers and roots.
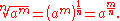
Problems can occur when taking the nth roots of negative or complex number
s. For instance:

whereas
when taking the principal value
of the roots. See failure of power and logarithm identities in the exponentiation article for more details.
For example, to write the radical expression in simplified form, we can proceed as follows. First, look for a perfect square under the square root sign and remove it:
in simplified form, we can proceed as follows. First, look for a perfect square under the square root sign and remove it: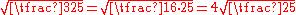
Next, there is a fraction under the radical sign, which we change as follows:
Finally, we remove the radical from the denominator as follows: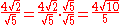
When there is a denominator involving surds it may be possible to find a factor to multiply both numerator and denominator by to simplify the expression. For instance using the factorization of the sum of two cubes:
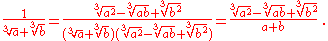
Simplifying radical expressions involving nested radicals can be quite difficult. It is not immediately obvious for instance that:
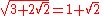

with . This expression can be derived from the binomial series
. This expression can be derived from the binomial series
.

The nth root of a number A can be computed by the nth root algorithm, a special case of Newton's method
. Start with an initial guess x0 and then iterate using the recurrence relation
until the desired precision is reached.
Depending on the application, it may be enough to use only the first Newton approximant: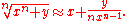
For example, to find the fifth root of 34, note that 25 = 32 and thus take x = 32 and y = 2 in the above formula. This yields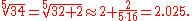
The error in the approximation is only about 0.03 %.
Newton's method can be extended to produce a generalized continued fraction for the nth root which can be modified in various ways as described in that article. For example:


In the case of the fifth root of 34 above (after dividing out common factors):
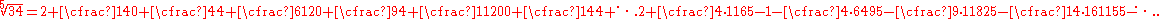
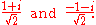
If we express a complex number in polar form, then the square root can be obtained by taking the square root of the radius and halving the angle:
A principal root of a complex number may be chosen in various ways, for example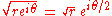
which introduces a branch cut in the complex plane
along the positive real axis with the condition 0 ≤ θ < 2π, and along the negative real axis with −π < θ ≤ π.
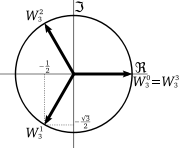 The number 1 has n different nth roots in the complex plane, namely
The number 1 has n different nth roots in the complex plane, namely
where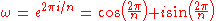
These roots are evenly spaced around the unit circle
in the complex plane, at angles which are multiples of . For example, the square roots of unity are 1 and −1, and the fourth roots of unity are 1,
. For example, the square roots of unity are 1 and −1, and the fourth roots of unity are 1, 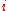 , −1, and
, −1, and 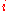 .
.

where η is a single nth root, and 1, ω, ω2, ... ωn−1 are the nth roots of unity. For example, the four different fourth roots of 2 are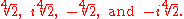
In polar form, a single nth root may be found by the formula
As with square roots, the formula above cannot be applied consistently to the entire complex plane, but instead leads to a branch cut at the points where θ / n suddenly “jumps”.
s could be expressed in terms of radicals and elementary operations
; however, the Abel-Ruffini theorem (1824) shows that this is not true in general. For example, the solutions of the equation
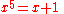
cannot be expressed in terms of radicals. (cf. quintic equation
)
For solving any equation of the nth degree numerically, see Root-finding algorithm
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the nth root of a number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
x is a number r which, when raised to the power of n, equals x

where n is the degree of the root. A root of degree 2 is usually called a square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
and a root of degree 3, a cube root.
For example:
- 2 is a square root of 4, since 22 = 4.
- −2 is also a square root of 4, since (−2)2 = 4.
A number may have many roots of degree n and the roots are not necessarily real numbers.
Roots are usually written using the radical symbol
 , with
, with  denoting the square root,
denoting the square root, 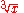 denoting the cube root,
denoting the cube root,  denoting the fourth root, and so on. In the expression
denoting the fourth root, and so on. In the expression  , n is called the index,
, n is called the index,  is the radical sign, and x is called the radicand. When a number is presented under the radical symbol, it must return only one result like a function
is the radical sign, and x is called the radicand. When a number is presented under the radical symbol, it must return only one result like a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, so a non-negative real root, called the principal nth root, is preferred rather than others. An unresolved root, especially one using the radical symbol, is often referred to as a surd or a radical. Any expression containing a radical, whether it is a square root, a cube root, or a higher root, is called a radical expression.
In calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, roots are treated as special cases of exponentiation, where the exponent is a fraction
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
:

Roots are particularly important in the theory of infinite series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
; the root test determines the radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
of a power series. Nth roots can also be defined for complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, and the complex roots of 1 (the roots of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
) play an important role in higher mathematics. Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
can be used to determine which algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s can be expressed using roots, and to prove the Abel-Ruffini theorem, which states that a general polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equation of degree five or higher cannot be solved using roots alone; this result is also known as "the insolubility of the quintic".
History
The origin of the root symbol √ is largely speculative. Some sources imply that the symbol was first used by Arabic mathematicians. One of those mathematicians was Abū al-Hasan ibn Alī al-QalasādīAbu al-Hasan ibn Ali al-Qalasadi
Abū al-Ḥasan ibn ʿAlī ibn Muḥammad ibn ʿAlī al-Qalaṣādī was a Muslim mathematician from Al-Andalus specializing in Islamic inheritance jurisprudence...
(1421–1486). Legend has it that it was taken from the Arabic letter ج, which is the first letter in the word Jadhir "root" in Arabic. (The dh in Jadhir is a voiced interdental fricative, like the th in English the.) Many scholars, however, including Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
believe it originates from the letter
Letter (alphabet)
A letter is a grapheme in an alphabetic system of writing, such as the Greek alphabet and its descendants. Letters compose phonemes and each phoneme represents a phone in the spoken form of the language....
r, the first letter of radix
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
"root" in Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
word referring to the same mathematical operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
. The symbol was first seen in print without the vinculum (the horizontal "bar" over the numbers inside the radical symbol) in the year 1525 in Die Coss by Christoff Rudolff, a German mathematician.
The term surd traces back to al-Khwārizmī (c. 825), who referred to rational and irrational numbers as audible and inaudible, respectively. This later led to the Arabic asamm (deaf, dumb) for irrational number being translated as surdus (deaf or mute) into Latin. Gherardo of Cremona (c. 1150), Fibonacci (1202) and then Robert Recorde (1551) all used the term to refer to unresolved irrational roots.
Definition and notation
The nth root of a number x, where n is a positive integer, is a number r whose nth power is x:
Every positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
x has a single positive nth root, which is written
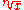 . For n equal to 2 this is called the square root and the n is omitted. The nth root can also be represented using exponentiation
. For n equal to 2 this is called the square root and the n is omitted. The nth root can also be represented using exponentiationExponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
as x1/n.
For even values of n, positive numbers also have a negative nth root, while negative numbers do not have a real nth root. For odd values of n, every negative number x has a real negative nth root. For example, −2 has a real 5th root,
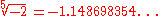 but −2 does not have any real 6th roots.
but −2 does not have any real 6th roots.Every non-zero number x, real or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, has n different complex number nth roots including any positive or negative roots, see complex roots below. The nth root of 0 is 0.
For most numbers, an nth root is irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
. For example,
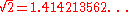
All nth roots of integers, or in fact of any algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
, are algebraic.
For the extension of powers and roots to indices that are not positive integers, see exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
.
The character codes for the radical symbols are
| Read | Character | Unicode Unicode Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems... | ASCII ASCII The American Standard Code for Information Interchange is a character-encoding scheme based on the ordering of the English alphabet. ASCII codes represent text in computers, communications equipment, and other devices that use text... | URL Uniform Resource Locator In computing, a uniform resource locator or universal resource locator is a specific character string that constitutes a reference to an Internet resource.... | HTML HTML HyperText Markup Language is the predominant markup language for web pages. HTML elements are the basic building-blocks of webpages.... (others) |
|---|---|---|---|---|---|
| Square root | U+221A | √ |
%E2%88%9A |
√ |
|
| Cube root | |
U+221B | ∛ |
%E2%88%9B |
|
| Fourth root | |
U+221C | ∜ |
%E2%88%9C |
Square roots
The square root of a number x is that number r which, when squared, becomes x:
Every positive real number has two square roots, one positive and one negative. For example, the two square roots of 25 are 5 and −5. The positive square root is also known as the principal square root, and is denoted with a radical sign:

Since the square of every real number is a positive real number, negative numbers do not have real square roots. However, every negative number has two imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
square roots. For example, the square roots of −25 are 5i and −5i, where i
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
represents a square root of −1.
Cube roots
A cube root of a number x is a number r whose cube is x:
Every real number x has exactly one real cube root, written
 . For example,
. For example,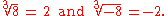
Every real number has two additional complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
cube roots (see complex roots below).
Identities and properties
Every positive real number has a positive nth root and the rules for operations with such surds are straightforward: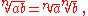

Using the exponent form as in
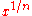 normally makes it easier to cancel out powers and roots.
normally makes it easier to cancel out powers and roots.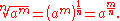
Problems can occur when taking the nth roots of negative or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. For instance:

whereas

when taking the principal value
Principal value
In considering complex multiple-valued functions in complex analysis, the principal values of a function are the values along one chosen branch of that function, so it is single-valued.-Motivation:...
of the roots. See failure of power and logarithm identities in the exponentiation article for more details.
Simplified form of a radical expression
A radical expression is said to be in simplified form if- There is no factor of the radicand that can be written as a power greater than or equal to the index.
- There are no fractions under the radical sign.
- There are no radicals in the denominator.
For example, to write the radical expression
 in simplified form, we can proceed as follows. First, look for a perfect square under the square root sign and remove it:
in simplified form, we can proceed as follows. First, look for a perfect square under the square root sign and remove it: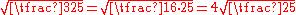
Next, there is a fraction under the radical sign, which we change as follows:

Finally, we remove the radical from the denominator as follows:
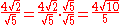
When there is a denominator involving surds it may be possible to find a factor to multiply both numerator and denominator by to simplify the expression. For instance using the factorization of the sum of two cubes:
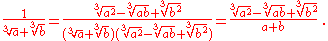
Simplifying radical expressions involving nested radicals can be quite difficult. It is not immediately obvious for instance that:
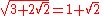
Infinite series
The radical or root may be represented by the infinite series:
with
 . This expression can be derived from the binomial series
. This expression can be derived from the binomial seriesBinomial series
In mathematics, the binomial series is the Taylor series at x = 0 of the function f given by f = α, where is an arbitrary complex number...
.
Computing principal roots
The nth root of an integer is not always an integer or rational number. For instance, the fifth root of 34 is
The nth root of a number A can be computed by the nth root algorithm, a special case of Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
. Start with an initial guess x0 and then iterate using the recurrence relation

until the desired precision is reached.
Depending on the application, it may be enough to use only the first Newton approximant:
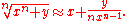
For example, to find the fifth root of 34, note that 25 = 32 and thus take x = 32 and y = 2 in the above formula. This yields
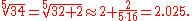
The error in the approximation is only about 0.03 %.
Newton's method can be extended to produce a generalized continued fraction for the nth root which can be modified in various ways as described in that article. For example:


In the case of the fifth root of 34 above (after dividing out common factors):
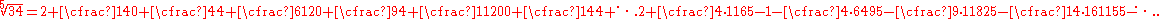
Square roots
The two square roots of a complex number are always negatives of each other. For example, the square roots of −4 are 2i and −2i, and the square roots of i are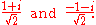
If we express a complex number in polar form, then the square root can be obtained by taking the square root of the radius and halving the angle:

A principal root of a complex number may be chosen in various ways, for example
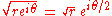
which introduces a branch cut in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
along the positive real axis with the condition 0 ≤ θ < 2π, and along the negative real axis with −π < θ ≤ π.
Roots of unity


where
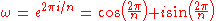
These roots are evenly spaced around the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
in the complex plane, at angles which are multiples of
 . For example, the square roots of unity are 1 and −1, and the fourth roots of unity are 1,
. For example, the square roots of unity are 1 and −1, and the fourth roots of unity are 1, 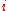 , −1, and
, −1, and 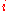 .
.nth roots
Every complex number has n different nth roots in the complex plane. These are
where η is a single nth root, and 1, ω, ω2, ... ωn−1 are the nth roots of unity. For example, the four different fourth roots of 2 are
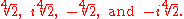
In polar form, a single nth root may be found by the formula

As with square roots, the formula above cannot be applied consistently to the entire complex plane, but instead leads to a branch cut at the points where θ / n suddenly “jumps”.
Solving polynomials
It was once believed that all roots of polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s could be expressed in terms of radicals and elementary operations
Elementary arithmetic
Elementary arithmetic is the simplified portion of arithmetic which is considered necessary and appropriate during primary education. It includes the operations of addition, subtraction, multiplication, and division. It is taught in elementary school....
; however, the Abel-Ruffini theorem (1824) shows that this is not true in general. For example, the solutions of the equation
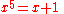
cannot be expressed in terms of radicals. (cf. quintic equation
Quintic equation
In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
)
For solving any equation of the nth degree numerically, see Root-finding algorithm
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
.
See also
- Nth root algorithm
- Shifting nth-root algorithmShifting nth-root algorithmThe shifting nth root algorithm is an algorithm for extracting the nth root of a positive real number which proceeds iteratively by shifting in n digits of the radicand, starting with the most significant, and produces one digit of the root on each iteration, in a manner similar to long...
- Irrational numberIrrational numberIn mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
- Algebraic numberAlgebraic numberIn mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
- Nested radical
- Twelfth root of two
- Super-root

