
Bhaskara I
Encyclopedia
Bhāskara ( commonly called Bhaskara I to avoid confusion with the 12th century mathematician Bhāskara II) was a 7th century India
n mathematician
, who was apparently the first to write numbers in the Hindu-Arabic
decimal system
with a circle for the zero
, and who gave a unique and remarkable rational approximation
of the sine
function in his commentary on Aryabhata
's work. This commentary, Āryabhaṭīyabhāṣya, written in 629 CE, is the oldest known prose work in Sanskrit on mathematics and astronomy. He also wrote two astronomical works in the line of Aryabhata's school, the Mahābhāskarīya and the Laghubhāskarīya.
He was born at Bori, in Parbhani district of Maharashtra state in India in 7th century.
His astronomical education was given by his father. Bhaskara is considered the most important scholar of Aryabhata
's astronomical school. He and Brahmagupta
are the most renowned Indian mathematicians who made considerable contributions to the study of fractions.
system, these words were aligned such that each number assigns the factor of the power of ten corresponding to its position, only in reverse order: the higher powers were right from the lower ones.
His system is truly positional, since the same words representing, can also be used to represent the values 40 or 400. Quite remarkably, he often explains a number given in this system, using the formula ankair api ("in figures this reads"), by repeating it written with the first nine Brahmi numeral
s, using a small circle for the zero
. Contrary to his word number system, however, the figures are written in descending valuedness from left to right, exactly as we do it today. Therefore, at least since 629 the decimal
Presumably, Bhaskara did not invent it, but he was the first having no compunctions to use the Brahmi numeral
s in a scientific contribution in Sanskrit
.
His work Mahabhaskariya divides into eight chapters about mathematical astronomy. In chapter 7, he gives a remarkable approximation formula for sin x, that is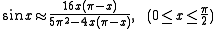
which he assigns to Aryabhata
. It reveals a relative error of less than 1.9% (the greatest deviation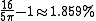 at
at 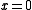 ). Moreover, relations between sine and cosine, as well as between the sine of an angle >90° >180° or >270° to the sine of an angle <90° are given.
). Moreover, relations between sine and cosine, as well as between the sine of an angle >90° >180° or >270° to the sine of an angle <90° are given.
Parts of Mahabhaskariya were later translated into Arabic.
Bhaskara already dealt with the assertion that if p is a prime number, then 1 + (p–1)! is divisible by p. It was proved later by Al-Haitham, also mentioned by Fibonacci
, and is now known as Wilson's theorem.
Moreover, Bhaskara stated theorems about the solutions of today so called Pell equations
. For instance, he posed the problem: "Tell me, O mathematician, what is that square which multiplied by 8 becomes - together with unity - a square?" In modern notation, he asked for the solutions of the Pell equation
 . It has the simple solution x = 1, y = 3, or shortly (x,y) = (1,3), from which further solutions can be constructed, e.g., (x,y) = (6,17).
. It has the simple solution x = 1, y = 3, or shortly (x,y) = (1,3), from which further solutions can be constructed, e.g., (x,y) = (6,17).
India
India , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
n mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, who was apparently the first to write numbers in the Hindu-Arabic
Hindu-Arabic numeral system
The Hindu–Arabic numeral system or Hindu numeral system is a positional decimal numeral system developed between the 1st and 5th centuries by Indian mathematicians, adopted by Persian and Arab mathematicians , and spread to the western world...
decimal system
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
with a circle for the zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, and who gave a unique and remarkable rational approximation
Approximation
An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...
of the sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
function in his commentary on Aryabhata
Aryabhata
Aryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
's work. This commentary, Āryabhaṭīyabhāṣya, written in 629 CE, is the oldest known prose work in Sanskrit on mathematics and astronomy. He also wrote two astronomical works in the line of Aryabhata's school, the Mahābhāskarīya and the Laghubhāskarīya.
Biography
Little is known about Bhāskara's life. He was "probably a Marathi astronomer".He was born at Bori, in Parbhani district of Maharashtra state in India in 7th century.
His astronomical education was given by his father. Bhaskara is considered the most important scholar of Aryabhata
Aryabhata
Aryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
's astronomical school. He and Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
are the most renowned Indian mathematicians who made considerable contributions to the study of fractions.
Representation of numbers
Chandua probably most important mathematical contribution concerns the representation of numbers in a positional system. The first positional representations were known to Indian astronomers about 500. However, the numbers were not written in figures, but in words or allegories, and were organized in verses. For instance, the number 1 was given as moon, since it exists only once; the number 2 was represented by wings, twins, or eyes, since they always occur in pairs; the number 5 was given by the (5) senses. Similar to our current decimalDecimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
system, these words were aligned such that each number assigns the factor of the power of ten corresponding to its position, only in reverse order: the higher powers were right from the lower ones.
His system is truly positional, since the same words representing, can also be used to represent the values 40 or 400. Quite remarkably, he often explains a number given in this system, using the formula ankair api ("in figures this reads"), by repeating it written with the first nine Brahmi numeral
Brahmi numeral
The Brahmi numerals are an indigenous Indian numeral system attested from the 3rd century BCE . They are the direct graphic ancestors of the modern Indic and Hindu-Arabic numerals. However, they were conceptually distinct from these later systems, as they were not used as a positional system with a...
s, using a small circle for the zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
. Contrary to his word number system, however, the figures are written in descending valuedness from left to right, exactly as we do it today. Therefore, at least since 629 the decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
Presumably, Bhaskara did not invent it, but he was the first having no compunctions to use the Brahmi numeral
Brahmi numeral
The Brahmi numerals are an indigenous Indian numeral system attested from the 3rd century BCE . They are the direct graphic ancestors of the modern Indic and Hindu-Arabic numerals. However, they were conceptually distinct from these later systems, as they were not used as a positional system with a...
s in a scientific contribution in Sanskrit
Sanskrit
Sanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
.
Further contributions
Bhaskara wrote three astronomical contributions. In 629 he commented the Aryabhatiya, written in verses, about mathematical astronomy. The comments referred exactly to the 33 verses dealing with mathematics. There he considered variable equations and trigonometric formulae.His work Mahabhaskariya divides into eight chapters about mathematical astronomy. In chapter 7, he gives a remarkable approximation formula for sin x, that is
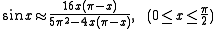
which he assigns to Aryabhata
Aryabhata
Aryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
. It reveals a relative error of less than 1.9% (the greatest deviation
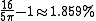 at
at 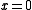 ). Moreover, relations between sine and cosine, as well as between the sine of an angle >90° >180° or >270° to the sine of an angle <90° are given.
). Moreover, relations between sine and cosine, as well as between the sine of an angle >90° >180° or >270° to the sine of an angle <90° are given.Parts of Mahabhaskariya were later translated into Arabic.
Bhaskara already dealt with the assertion that if p is a prime number, then 1 + (p–1)! is divisible by p. It was proved later by Al-Haitham, also mentioned by Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
, and is now known as Wilson's theorem.
Moreover, Bhaskara stated theorems about the solutions of today so called Pell equations
Pell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
. For instance, he posed the problem: "Tell me, O mathematician, what is that square which multiplied by 8 becomes - together with unity - a square?" In modern notation, he asked for the solutions of the Pell equation
Pell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
 . It has the simple solution x = 1, y = 3, or shortly (x,y) = (1,3), from which further solutions can be constructed, e.g., (x,y) = (6,17).
. It has the simple solution x = 1, y = 3, or shortly (x,y) = (1,3), from which further solutions can be constructed, e.g., (x,y) = (6,17).Further reading
- H.-W. Alten, A. Djafari Naini, M. Folkerts, H. Schlosser, K.-H. Schlote, H. Wußing: 4000 Jahre Algebra. Springer-Verlag Berlin Heidelberg 2003 [ISBN 3-540-43554-9], §3.2.1
- S. Gottwald, H.-J. Ilgauds, K.-H. Schlote (Hrsg.): Lexikon bedeutender Mathematiker. Verlag Harri Thun, Frankfurt a. M. 1990 [ISBN 3-8171-1164-9]
- G. Ifrah: The Universal History of Numbers. John Wiley & Sons, New York 2000 [ISBN 0-471-39340-1]..
Source texts
(From )- M. C. Apaṭe. The Laghubhāskarīya, with the commentary of Parameśvara. Anandāśrama, Sanskrit series no. 128, Poona, 1946.
- K. Sastri. Mahābhāskarīya of Bhāskarācārya with the Bhāṣya of Govindasvāmin and Supercommentary Siddhāntadīpikā of Parameśvara. Madras Govt. Oriental series, no. cxxx, 1957.
- K. S. Shukla. Mahābhāskarīya, Edited and Translated into English, with Explanatory and Critical Notes, and Comments, etc. Department of mathematics, Lucknow University, 1960.
- K. S. Shukla. Laghubhāskarīya, Edited and Translated into English, with Explanatory and Critical Notes, and Comments, etc., Department of mathematics and astronomy, Lucknow University, 1963.
- K. S. Shukla. Āryabhaṭīya of Āryabhaṭa, with the commentary of Bhāskara I and Someśvara. Indian National Science Academy (INSA), New- Delhi, 1976.

