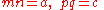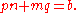Factorization
Encyclopedia
In mathematics
, factorization (also factorisation in British English) or factoring is the decomposition of an object (for example, a number
, a polynomial
, or a matrix
) into a product
of other objects, or factors, which when multiplied
together give the original. For example, the number 15 factors into primes
as 3 × 5, and the polynomial x2 − 4 factors as (x − 2)(x + 2). In all cases, a product of simpler objects is obtained.
The aim of factoring is usually to reduce something to "basic building blocks," such as numbers to prime numbers, or polynomials to irreducible polynomial
s. Factoring integers is covered by the fundamental theorem of arithmetic
and factoring polynomials
by the fundamental theorem of algebra
. Viète's formulas relate the coefficients of a polynomial to its roots.
The opposite of polynomial factorization is expansion
, the multiplying together of polynomial factors
to a "expanded" polynomial, written as just a sum of terms.
Integer factorization
for large integers appears to be a difficult problem. There is no known method to carry it out quickly. Its complexity is the basis of the assumed security of some public key cryptography algorithms, such as RSA.
A matrix can also be factorized into a product of matrices of special types, for an application in which that form is convenient. One major example of this uses an orthogonal
or unitary matrix, and a triangular matrix
. There are different types: QR decomposition
, LQ, QL, RQ, RZ.
Another example is the factorization of a function
as the composition
of other functions having certain properties; for example, every function can be viewed as the composition of a surjective function
with an injective function
. This situation is generalized by factorization system
s.
, every positive integer
greater than 1 has a unique prime factorization. Given an algorithm for integer factorization, one can factor any integer down to its constituent primes by repeated application of this algorithm. For very large numbers, no efficient algorithm
is known.
over the complex numbers (polynomials of the form where
where  ,
,  , and
, and  ∈
∈  ) can be factored into an expression
) can be factored into an expression
with the form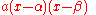 using the quadratic formula. The method is as follows:
using the quadratic formula. The method is as follows:

where and
and 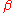 are the two roots of the polynomial, found with the quadratic formula.
are the two roots of the polynomial, found with the quadratic formula.
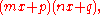
where
and
You can then set each binomial equal to zero, and solve for x to reveal the two roots. Factoring does not involve any other formulas, and is mostly just something you see when you come upon a quadratic equation.
Take for example 2x2 − 5x + 2 = 0. Because a = 2 and mn = a, mn = 2, which means that of m and n, one is 1 and the other is 2. Now we have (2x + p)(x + q) = 0. Because c = 2 and pq = c, pq = 2, which means that of p and q, one is 1 and the other is 2 or one is −1 and the other is −2. A guess and check of substituting the 1 and 2, and −1 and −2, into p and q (while applying pn + mq = b) tells us that 2x2 − 5x + 2 = 0 factors into (2x − 1)(x − 2) = 0, giving us the roots x = {0.5, 2}
Note: A quick way to check whether the second term in the binomial should be positive or negative (in the example, 1 and 2 and −1 and −2) is to check the second operation in the trinomial (+ or −). If it is +, then check the first operation: if it is +, the terms will be positive, while if it is −, the terms will be negative. If the second operation is −, there will be one positive and one negative term; guess and check is the only way to determine which one is positive and which is negative.
If a polynomial with integer coefficients has a discriminant
that is a perfect square, that polynomial is factorable over the integers.
For example, look at the polynomial 2x2 + 2x − 12. If you substitute the values of the expression into the quadratic formula, the discriminant b2 − 4ac becomes 22 − 4 × 2 × −12, which equals 100. 100 is a perfect square, so the polynomial 2x2 + 2x − 12 is factorable over the integers; its factors are 2, (x − 2), and (x + 3).
Now look at the polynomial x2 + 93x − 2. Its discriminant, 932 − 4 × 1 × (−2), is equal to 8657, which is not a perfect square. So x2 + 93x − 2 cannot be factored over the integers.
 Some quadratics can be factored into two identical binomials. These quadratics are called perfect square trinomials. Perfect square trinomials can be factored as follows:
Some quadratics can be factored into two identical binomials. These quadratics are called perfect square trinomials. Perfect square trinomials can be factored as follows:
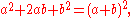
and
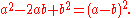
. It is the application of the formula

to any two terms, whether or not they are perfect squares. If the two terms are subtracted, simply apply the formula. If they are added, the two binomials obtained from the factoring will each have an imaginary term. This formula can be represented as

For example, can be factored into
can be factored into 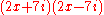 .
.
Factoring by grouping is done by placing the terms in the polynomial into two or more groups, where each group can be factored by a known method. The results of these factorizations can sometimes be combined to make an even more simplified expression. For example, to factor the polynomial

Group similar terms,
Factor out Greatest Common Factor,
Factor out binomial
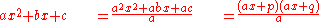
The terms on top will have common factors that can be factored out and used to cancel the denominator, if it is not 1. As an example consider the quadratic polynomial:
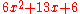
Inspection of the factors of ac = 36 leads to 4 + 9 = 13 = b.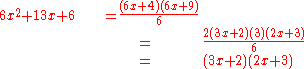
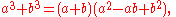
and the difference by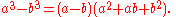

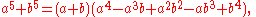
and the difference by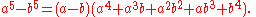
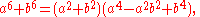
and the difference by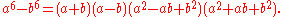
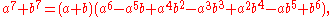
and the difference by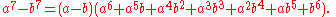

and multiplying by the (x -1) factor, the desired result is found. To give the general
form as above, we can replace x by a/b and multiply both sides by bn.
This gives the general form for the difference of two nth powers as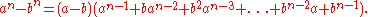
The corresponding sum of two nth powers depends on whether n is even or odd.
If n is odd, b can be replaced by -b in the above formula. If n is even, the form is somewhat more
tedious.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, factorization (also factorisation in British English) or factoring is the decomposition of an object (for example, a number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
, a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
, or a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
) into a product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of other objects, or factors, which when multiplied
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
together give the original. For example, the number 15 factors into primes
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
as 3 × 5, and the polynomial x2 − 4 factors as (x − 2)(x + 2). In all cases, a product of simpler objects is obtained.
The aim of factoring is usually to reduce something to "basic building blocks," such as numbers to prime numbers, or polynomials to irreducible polynomial
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
s. Factoring integers is covered by the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
and factoring polynomials
Polynomial factorization
In mathematics and computer algebra, polynomial factorization refers to factoring a polynomial into irreducible polynomials over a given field.-Formulation of the question:...
by the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
. Viète's formulas relate the coefficients of a polynomial to its roots.
The opposite of polynomial factorization is expansion
Polynomial expansion
In mathematics, an expansion of a product of sums expresses it as a sum of products by using the fact that multiplication distributes over addition...
, the multiplying together of polynomial factors
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
to a "expanded" polynomial, written as just a sum of terms.
Integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
for large integers appears to be a difficult problem. There is no known method to carry it out quickly. Its complexity is the basis of the assumed security of some public key cryptography algorithms, such as RSA.
A matrix can also be factorized into a product of matrices of special types, for an application in which that form is convenient. One major example of this uses an orthogonal
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
or unitary matrix, and a triangular matrix
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
. There are different types: QR decomposition
QR decomposition
In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
, LQ, QL, RQ, RZ.
Another example is the factorization of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
as the composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of other functions having certain properties; for example, every function can be viewed as the composition of a surjective function
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
with an injective function
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
. This situation is generalized by factorization system
Factorization system
In mathematics, it can be shown that every function can be written as the composite of a surjective function followed by an injective function. Factorization systems are a generalization of this situation in category theory.-Definition:...
s.
Integers
By the fundamental theorem of arithmeticFundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
, every positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
greater than 1 has a unique prime factorization. Given an algorithm for integer factorization, one can factor any integer down to its constituent primes by repeated application of this algorithm. For very large numbers, no efficient algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
is known.
Quadratic polynomials
Any quadratic polynomialQuadratic polynomial
In mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2...
over the complex numbers (polynomials of the form
 where
where  ,
,  , and
, and  ∈
∈  ) can be factored into an expression
) can be factored into an expressionExpression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
with the form
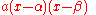 using the quadratic formula. The method is as follows:
using the quadratic formula. The method is as follows:
where
 and
and 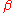 are the two roots of the polynomial, found with the quadratic formula.
are the two roots of the polynomial, found with the quadratic formula.Polynomials factorable over the integers
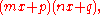
where
and
You can then set each binomial equal to zero, and solve for x to reveal the two roots. Factoring does not involve any other formulas, and is mostly just something you see when you come upon a quadratic equation.
Take for example 2x2 − 5x + 2 = 0. Because a = 2 and mn = a, mn = 2, which means that of m and n, one is 1 and the other is 2. Now we have (2x + p)(x + q) = 0. Because c = 2 and pq = c, pq = 2, which means that of p and q, one is 1 and the other is 2 or one is −1 and the other is −2. A guess and check of substituting the 1 and 2, and −1 and −2, into p and q (while applying pn + mq = b) tells us that 2x2 − 5x + 2 = 0 factors into (2x − 1)(x − 2) = 0, giving us the roots x = {0.5, 2}
Note: A quick way to check whether the second term in the binomial should be positive or negative (in the example, 1 and 2 and −1 and −2) is to check the second operation in the trinomial (+ or −). If it is +, then check the first operation: if it is +, the terms will be positive, while if it is −, the terms will be negative. If the second operation is −, there will be one positive and one negative term; guess and check is the only way to determine which one is positive and which is negative.
If a polynomial with integer coefficients has a discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
that is a perfect square, that polynomial is factorable over the integers.
For example, look at the polynomial 2x2 + 2x − 12. If you substitute the values of the expression into the quadratic formula, the discriminant b2 − 4ac becomes 22 − 4 × 2 × −12, which equals 100. 100 is a perfect square, so the polynomial 2x2 + 2x − 12 is factorable over the integers; its factors are 2, (x − 2), and (x + 3).
Now look at the polynomial x2 + 93x − 2. Its discriminant, 932 − 4 × 1 × (−2), is equal to 8657, which is not a perfect square. So x2 + 93x − 2 cannot be factored over the integers.
Perfect square trinomials

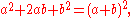
and
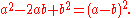
Sum/difference of two squares
Another common type of algebraic factoring is called the difference of two squaresDifference of two squares
In mathematics, the difference of two squares, or the difference of perfect squares, is when a number is squared, or multiplied by itself, and is then subtracted from another squared number...
. It is the application of the formula

to any two terms, whether or not they are perfect squares. If the two terms are subtracted, simply apply the formula. If they are added, the two binomials obtained from the factoring will each have an imaginary term. This formula can be represented as

For example,
 can be factored into
can be factored into 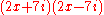 .
.Factoring by grouping
Another way to factor some polynomials is factoring by grouping. For those who like algorithms, "factoring by grouping" may be the best way to approach factoring a trinomial, as it takes the guess work out of the process.Factoring by grouping is done by placing the terms in the polynomial into two or more groups, where each group can be factored by a known method. The results of these factorizations can sometimes be combined to make an even more simplified expression. For example, to factor the polynomial

Group similar terms,

Factor out Greatest Common Factor,

Factor out binomial

AC Method
If a quadratic polynomial has rational solutions, we can find p and q so that pq = ac and p + q = b. (If the discriminant is a square number these exist, otherwise we have irrational or complex solutions, and the assumption of rational solutions is not valid.)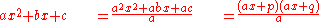
The terms on top will have common factors that can be factored out and used to cancel the denominator, if it is not 1. As an example consider the quadratic polynomial:
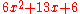
Inspection of the factors of ac = 36 leads to 4 + 9 = 13 = b.
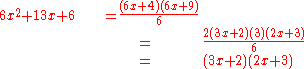
Sum/difference of two cubes
Another formula for factoring is the sum or difference of two cubes. The sum can be represented by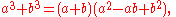
and the difference by
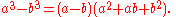
Difference of two fourth powers
Another formula is the difference of two fourth powers, which is
Sum/difference of two fifth powers
Another formula for factoring is the sum or difference of two fifth powers. The sum can be represented by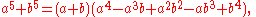
and the difference by
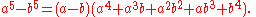
Sum/difference of two sixth powers
Then there's the formula for factoring the sum or difference of two sixth powers. The sum can be represented by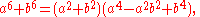
and the difference by
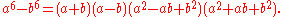
Sum/difference of two seventh powers
And last there's the formula for factoring the sum or difference of two seventh powers. The sum can be represented by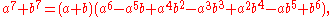
and the difference by
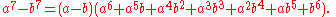
Difference of nth powers
This factorization can be extended to any positive integer power n by use of the geometric series. By noting that
and multiplying by the (x -1) factor, the desired result is found. To give the general
form as above, we can replace x by a/b and multiply both sides by bn.
This gives the general form for the difference of two nth powers as
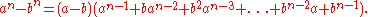
The corresponding sum of two nth powers depends on whether n is even or odd.
If n is odd, b can be replaced by -b in the above formula. If n is even, the form is somewhat more
tedious.
See also
- Completing the squareCompleting the squareIn elementary algebra, completing the square is a technique for converting a quadratic polynomial of the formax^2 + bx + c\,\!to the formIn this context, "constant" means not depending on x. The expression inside the parenthesis is of the form ...
- Factorization of polynomials
- Factor theoremFactor theoremIn algebra, the factor theorem is a theorem linking factors and zeros of a polynomial. It is a special case of the polynomial remainder theorem.The factor theorem states that a polynomial f has a factor if and only if f=0....
- FOIL ruleFOIL ruleIn elementary algebra, FOIL is a mnemonic for the standard method of multiplying two binomials—hence the method may be referred to as the FOIL method...
- Matrix decompositionMatrix decompositionIn the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
- Pascal's trianglePascal's triangleIn mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
- Prime factorPrime factorIn number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
- Program synthesisProgram synthesisProgram synthesis is a special form of automatic programming that is most often paired with a technique for formal verification. The goal is to automatically construct a program that provably satisfies a given high-level specification...
- Table of Gaussian integer factorizationsTable of Gaussian integer factorizationsGaussian integers may be categorized as zero, the four units, Gaussian primes and composites. This is a list of Gaussian Integers in the first quadrant followed either by an explicit factorization or followed by a label for primes. The factorizations take the form of an optional unit multiplied...
- Unique factorizationUnique factorization domainIn mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
External links
- One hundred million numbers factored on html pages.
- A page about factorization, Algebra, Factoring
- WIMS Factoris is an online factorization tool.
- Wolfram AlphaWolfram AlphaWolfram Alpha is an answer-engine developed by Wolfram Research. It is an online service that answers factual queries directly by computing the answer from structured data, rather than providing a list of documents or web pages that might contain the answer as a search engine might...
can factorize too.