
Complex plane
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis. It can be thought of as a modified Cartesian plane, with the real part of a complex number represented by a displacement along the x-axis, and the imaginary part by a displacement along the y-axis.
The complex plane is sometimes called the Argand plane because it is used in Argand diagrams. These are named after Jean-Robert Argand
Jean-Robert Argand
Jean-Robert Argand was a gifted amateur mathematician. In 1806, while managing a bookstore in Paris, he published the idea of geometrical interpretation of complex numbers known as the Argand diagram.-Life:...
(1768–1822), although they were first described by Norwegian-Danish land surveyor and mathematician Caspar Wessel
Caspar Wessel
Caspar Wessel was a Norwegian-Danish mathematician and cartographer. In 1799, Wessel was the first person to describe the complex numbers. He was the younger brother of poet and playwright Johan Herman Wessel....
(1745–1818). Argand diagrams are frequently used to plot the positions of the poles and zeroes
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
of a function in the complex plane.
The concept of the complex plane allows a geometric interpretation of complex numbers. Under addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, they add like vectors. The multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
of two complex numbers can be expressed most easily in polar coordinates – the magnitude or modulus of the product is the product of the two absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
s, or moduli, and the angle or argument of the product is the sum of the two angles, or arguments. In particular, multiplication by a complex number of modulus 1 acts as a rotation.
Notational conventions
In complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
the complex numbers are customarily represented by the symbol z, which can be separated into its real (x) and imaginary (y) parts, like this:

for example: z = 4 + i5,
where x and y are real numbers, and i is the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
. In this customary notation the complex number z corresponds to the point (x, y) in the Cartesian plane
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
.
In the Cartesian plane the point (x, y) can also be represented in polar coordinates as
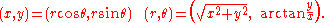
In the Cartesian plane it may be assumed that the arctangent
Inverse trigonometric function
In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions with suitably restricted domains .The notations sin−1, cos−1, etc...
takes values from −π/2 to π/2 (in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s), and some care must be taken to define the real arctangent function for points (x, y) when x ≤ 0. In the complex plane these polar coordinates take the form
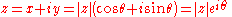
where

Here |z| is the absolute value or modulus of the complex number z; θ, the argument of z, is usually taken on the interval 0 ≤ θ < 2π; and the last equality (to |z|eiθ) is taken from Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
. Notice that the argument of z is multi-valued, because the complex exponential function is periodic, with period 2πi. Thus, if θ is one value of arg(z), the other values are given by arg(z) = θ + 2nπ, where n is any integer ≠ 0. While seldom used explicitly, the geometric view of the complex numbers is implicitly based on its structure of a Euclidean vector space of dimension 2, where the inner product of complex numbers and is given by
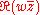 ; then for a complex number its absolute value || coincides with its Euclidean norm, and its argument with the angle turning from 1 to .
; then for a complex number its absolute value || coincides with its Euclidean norm, and its argument with the angle turning from 1 to .The theory of contour integration comprises a major part of complex analysis. In this context the direction of travel around a closed curve is important – reversing the direction in which the curve is traversed multiplies the value of the integral by −1. By convention the positive direction is counterclockwise. For example, the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
is traversed in the positive direction when we start at the point z = 1, then travel up and to the left through the point z = i, then down and to the left through −1, then down and to the right through −i, and finally up and to the right to z = 1, where we started.
Almost all of complex analysis is concerned with complex functions – that is, with functions that map some subset of the complex plane into some other (possibly overlapping, or even identical) subset of the complex plane. Here it is customary to speak of the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of f(z) as lying in the z-plane, while referring to the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
or image of f(z) as a set of points in the w-plane. In symbols we write
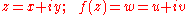
and often think of the function f as a transformation of the z-plane (with coordinates (x, y)) into the w-plane (with coordinates (u, v)).
Stereographic projections
It can be useful to think of the complex plane as if it occupied the surface of a sphere. Given a sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
of unit radius, place its center at the origin of the complex plane, oriented so that the equator on the sphere coincides with the unit circle in the plane, and the north pole is "above" the plane.
We can establish a one-to-one correspondence
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the points on the surface of the sphere minus the north pole and the points in the complex plane as follows. Given a point in the plane, draw a straight line connecting it with the north pole on the sphere. That line will intersect the surface of the sphere in exactly one other point. The point z = 0 will be projected onto the south pole of the sphere. Since the interior of the unit circle lies inside the sphere, that entire region (|z| < 1) will be mapped onto the southern hemisphere. The unit circle itself (|z| = 1) will be mapped onto the equator, and the exterior of the unit circle (|z| > 1) will be mapped onto the northern hemisphere, minus the north pole. Clearly this procedure is reversible – given any point on the surface of the sphere that is not the north pole, we can draw a straight line connecting that point to the north pole and intersecting the flat plane in exactly one point.
Under this stereographic projection the north pole itself is not associated with any point in the complex plane. We perfect the one-to-one correspondence by adding one more point to the complex plane – the so-called point at infinity—and identifying it with the north pole on the sphere. This topological space, the complex plane plus the point at infinity, is known as the extended complex plane
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. We speak of a single "point at infinity" when discussing complex analysis. There are two points at infinity (positive, and negative) on the real number line, but there is only one point at infinity (the north pole) in the extended complex plane.
Imagine for a moment what will happen to the lines of latitude and longitude when they are projected from the sphere onto the flat plane. The lines of latitude are all parallel to the equator, so they will become perfect circles centered on the origin z = 0. And the lines of longitude will become straight lines passing through the origin (and also through the "point at infinity", since they pass through both the north and south poles on the sphere).
This is not the only possible yet plausible stereographic situation of the projection of a sphere onto a plane consisting of two or more values. For instance, the north pole of the sphere might be placed on top of the origin z = -1 in a plane that's tangent to the circle. The details don't really matter. Any stereographic projection of a sphere onto a plane will produce one "point at infinity", and it will map the lines of latitude and longitude on the sphere into circles and straight lines, respectively, in the plane.
Cutting the plane
When discussing functions of a complex variable it is often convenient to think of a cut in the complex plane. This idea arises naturally in several different contexts.Multi-valued relationships and branch points
Consider the simple two-valued relationship
Before we can treat this relationship as a single-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, the range of the resulting value must be restricted somehow. When dealing with the square roots of non-negative real numbers this is easily done. For instance, we can just define
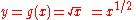
to be the non-negative real number y such that y2 = x. This idea doesn't work so well in the two-dimensional complex plane. To see why, let's think about the way the value of f(z) varies as the point z moves around the unit circle. We can write
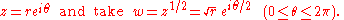
Evidently, as z moves all the way around the circle, w only traces out one-half of the circle. So one continuous motion in the complex plane has transformed the positive square root e0 = 1 into the negative square root eiπ = −1.
This problem arises because the point z = 0 has just one square root, while every other complex number z ≠ 0 has exactly two square roots. On the real number line we could circumvent this problem by erecting a "barrier" at the single point x = 0. A bigger barrier is needed in the complex plane, to prevent any closed contour from completely encircling the branch point
Branch point
In the mathematical field of complex analysis, a branch point of a multi-valued function is a point such that the function is discontinuous when going around an arbitrarily small circuit around this point...
z = 0. This is commonly done by introducing a branch cut; in this case the "cut" might extend from the point z = 0 along the positive real axis to the point at infinity, so that the argument of the variable z in the cut plane is restricted to the range 0 ≤ arg(z) < 2π.
We can now give a complete description of w = z½. To do so we need two copies of the z-plane, each of them cut along the real axis. On one copy we define the square root of 1 to be e0 = 1, and on the other we define the square root of 1 to be eiπ = −1. We call these two copies of the complete cut plane sheets. By making a continuity argument we see that the (now single-valued) function w = z½ maps the first sheet into the upper half of the w-plane, where 0 ≤ arg(w) < π, while mapping the second sheet into the lower half of the w-plane (where π ≤ arg(w) < 2π).
The branch cut in this example doesn't have to lie along the real axis. It doesn't even have to be a straight line. Any continuous curve connecting the origin z = 0 with the point at infinity would work. In some cases the branch cut doesn't even have to pass through the point at infinity. For example, consider the relationship
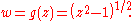
Here the polynomial z2 − 1 vanishes when z = ±1, so g evidently has two branch points. We can "cut" the plane along the real axis, from −1 to 1, and obtain a sheet on which g(z) is a single-valued function. Alternatively, the cut can run from z = 1 along the positive real axis through the point at infinity, then continue "up" the negative real axis to the other branch point, z = −1.
This situation is most easily visualized by using the stereographic projection described above. On the sphere one of these cuts runs longitudinally through the southern hemisphere, connecting a point on the equator (z = −1) with another point on the equator (z = 1), and passing through the south pole (the origin, z = 0) on the way. The second version of the cut runs longitudinally through the northern hemisphere and connects the same two equatorial points by passing through the north pole (that is, the point at infinity).
Restricting the domain of meromorphic functions
A meromorphic functionMeromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
is a complex function that is holomorphic
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
and therefore analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
everywhere in its domain except at a finite, or countably infinite
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
, number of points. The points at which such a function cannot be defined are called the poles of the meromorphic function. Sometimes all these poles lie in a straight line. In that case mathematicians may say that the function is "holomorphic on the cut plane". Here's a simple example.
The gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, defined by
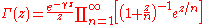
where γ is the Euler-Mascheroni constant
Euler-Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
, and has simple poles at 0, −1, −2, −3, ... because exactly one denominator in the infinite product vanishes when z is zero, or a negative integer. Since all its poles lie on the negative real axis, from z = 0 to the point at infinity, this function might be described as
"holomorphic on the cut plane, the cut extending along the negative real axis, from 0 (inclusive) to the point at infinity."
Alternatively, Γ(z) might be described as
"holomorphic in the cut plane with −π < arg(z) < π and excluding the point z = 0."
Notice that this cut is slightly different from the branch cut we've already encountered, because it actually excludes the negative real axis from the cut plane. The branch cut left the real axis connected with the cut plane on one side (0 ≤ θ), but severed it from the cut plane along the other side (θ < 2π).
Of course, it's not actually necessary to exclude the entire line segment from z = 0 to −∞ to construct a domain in which Γ(z) is holomorphic. All we really have to do is puncture the plane at a countably infinite set of points {0, −1, −2, −3, ...}. But a closed contour in the punctured plane might encircle one or more of the poles of Γ(z), giving a contour integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
that is not necessarily zero, by the residue theorem
Residue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
. By cutting the complex plane we ensure not only that Γ(z) is holomorphic in this restricted domain – we also ensure that the contour integral of Γ over any closed curve lying in the cut plane is identically equal to zero.
Specifying convergence regions
Many complex functions are defined by infinite seriesSeries (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
, or by continued fractions
Generalized continued fraction
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary real or complex values....
. A fundamental consideration in the analysis of these infinitely long expressions is identifying the portion of the complex plane in which they converge to a finite value. A cut in the plane may facilitate this process, as the following examples show.
Consider the function defined by the infinite series
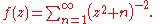
Since z2 = (−z)2 for every complex number z, it's clear that f(z) is an even function
Even and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
of z, so the analysis can be restricted to one half of the complex plane. And since the series is undefined when

it makes sense to cut the plane along the entire imaginary axis and establish the convergence of this series where the real part of z is not zero before undertaking the more arduous task of examining f(z) when z is a pure imaginary number.
In this example the cut is a mere convenience, because the points at which the infinite sum is undefined are isolated, and the cut plane can be replaced with a suitably punctured plane. In some contexts the cut is necessary, and not just convenient. Consider the infinite periodic continued fraction

It can be shown that f(z) converges to a finite value if and only if z is not a negative real number such that z < −¼. In other words, the convergence region for this continued fraction is the cut plane, where the cut runs along the negative real axis, from −¼ to the point at infinity.
Gluing the cut plane back together
We have already seen how the relationship
can be made into a single-valued function by splitting the domain of f into two disconnected sheets. It is also possible to "glue" those two sheets back together to form a single Riemann surface on which f(z) = z1/2 can be defined as a holomorphic function whose image is the entire w-plane (except for the point w = 0). Here's how that works.
Imagine two copies of the cut complex plane, the cuts extending along the positive real axis from z = 0 to the point at infinity. On one sheet define 0 ≤ arg(z) < 2π, so that 11/2 = e0 = 1, by definition. On the second sheet define 2π ≤ arg(z) < 4π, so that 11/2 = eiπ = −1, again by definition. Now flip the second sheet upside down, so the imaginary axis points in the opposite direction of the imaginary axis on the first sheet, with both real axes pointing in the same direction, and "glue" the two sheets together (so that the edge on the first sheet labeled "θ = 0" is connected to the edge labeled "θ < 4π" on the second sheet, and the edge on the second sheet labeled "θ = 2π" is connected to the edge labeled "θ < 2π" on the first sheet). The result is the Riemann surface domain on which f(z) = z1/2 is single-valued and holomorphic (except when z = 0).
To understand why f is single-valued in this domain, imagine a circuit around the unit circle, starting with z = 1 on the first sheet. When 0 ≤ θ < 2π we are still on the first sheet. When θ = 2π we have crossed over onto the second sheet, and are obliged to make a second complete circuit around the branch point z = 0 before returning to our starting point, where θ = 4π is equivalent to θ = 0, because of the way we glued the two sheets together. In other words, as the variable z makes two complete turns around the branch point, the image of z in the w-plane traces out just one complete circle.
Formal differentiation shows that
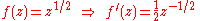
from which we can conclude that the derivative of f exists and is finite everywhere on the Riemann surface, except when z = 0 (that is, f is holomorphic, except when z = 0).
How can the Riemann surface for the function
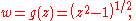
also discussed above, be constructed? Once again we begin with two copies of the z-plane, but this time each one is cut along the real line segment extending from z = −1 to z = 1 – these are the two branch points of g(z). We flip one of these upside down, so the two imaginary axes point in opposite directions, and glue the corresponding edges of the two cut sheets together. We can verify that g is a single-valued function on this surface by tracing a circuit around a circle of unit radius centered at z = 1. Commencing at the point z = 2 on the first sheet we turn halfway around the circle before encountering the cut at z = 0. The cut forces us onto the second sheet, so that when z has traced out one full turn around the branch point z = 1, w has taken just one-half of a full turn, the sign of w has been reversed (since eiπ = −1), and our path has taken us to the point z = 2 on the second sheet of the surface. Continuing on through another half turn we encounter the other side of the cut, where z = 0, and finally reach our starting point (z = 2 on the first sheet) after making two full turns around the branch point.
The natural way to label θ = arg(z) in this example is to set −π < θ ≤ π on the first sheet, with π < θ ≤ 3π on the second. The imaginary axes on the two sheets point in opposite directions so that the counterclockwise sense of positive rotation is preserved as a closed contour moves from one sheet to the other (remember, the second sheet is upside down). Imagine this surface embedded in a three-dimensional space, with both sheets parallel to the xy-plane. Then there appears to be a vertical hole in the surface, where the two cuts are joined together. What if the cut is made from z = −1 down the real axis to the point at infinity, and from z = 1, up the real axis until the cut meets itself? Again a Riemann surface can be constructed, but this time the "hole" is horizontal. Topologically speaking
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, both versions of this Riemann surface are equivalent – they are orientable two-dimensional surfaces of genus one.
Use of the complex plane in control theory
In control theoryControl theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, one use of the complex plane is known as the 's-plane'. It is used to visualise the roots of the equation describing a system's behaviour (the characteristic equation) graphically. The equation is normally expressed as a polynomial in the parameter 's' of the Laplace transform, hence the name 's' plane.
Another related use of the complex plane is with the Nyquist stability criterion
Nyquist stability criterion
When designing a feedback control system, it is generally necessary to determine whether the closed-loop system will be stable. An example of a destabilizing feedback control system would be a car steering system that overcompensates -- if the car drifts in one direction, the control system...
. This is a geometric principle which allows the stability of a closed-loop feedback system to be determined by inspecting a Nyquist plot
Nyquist plot
A Nyquist plot is a parametric plot of a transfer function used in automatic control and signal processing. The most common use of Nyquist plots is for assessing the stability of a system with feedback. In Cartesian coordinates, the real part of the transfer function is plotted on the X axis. The...
of its open-loop magnitude and phase response as a function of frequency (or loop transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
) in the complex plane.
The 'z-plane' is a discrete-time version of the s-plane, where z-transform
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
s are used instead of the Laplace transformation.
Other meanings of "complex plane"
The preceding sections of this article deal with the complex plane as the geometric analogue of the complex numbers. Although this usage of the term "complex plane" has a long and mathematically rich history, it is by no means the only mathematical concept that can be characterized as "the complex plane". There are at least three additional possibilities.- 1+1-dimensional Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, also known as the split-complex plane, is a "complex plane" in the sense that the algebraic split-complex numberSplit-complex numberIn abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s can be separated into two real components that are easily associated with the point (x, y) in the Cartesian plane. - The set of dual numberDual numberIn linear algebra, the dual numbers extend the real numbers by adjoining one new element ε with the property ε2 = 0 . The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra over the real numbers. Every dual number has the form z = a + bε with a and...
s over the reals can also be placed into one-to-one correspondence with the points (x, y) of the Cartesian plane, and represent another example of a "complex plane". - The vector space C×C, the Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of the complex numbers with themselves, is also a "complex plane" in the sense that it is a two-dimensional vector space whose coordinates are complex numbers.
Terminology
While the terminology "complex plane" is historically accepted, the object could be more appropriately named "complex line" as it is a 1-dimensional complex vector spaceComplex vector space
A complex vector space is a vector space over the complex numbers. It can also refer to:* a vector space over the real numbers with a linear complex structure...
.

