Riemann hypothesis - AbsoluteAstronomy.com

In mathematics, the Riemann hypothesis, proposed by , is a conjecture

Conjecture

A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...

about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros (as defined below) have real part 1/2. The name is also used for some closely related analogues, such as the Riemann hypothesis for curves over finite fields.

The Riemann hypothesis implies results about the distribution of prime numbers that are in some ways as good as possible. Along with suitable generalizations, it is considered by some mathematicians to be the most important unresolved problem in pure mathematics

Pure mathematics

Broadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...

. The Riemann hypothesis is part of Problem 8

Hilbert's eighth problem

Hilbert's eighth problem is one of David Hilbert's list of open mathematical problems posed in 1900. It concerns number theory, and in particular the Riemann hypothesis, although it is also concerned with the Goldbach Conjecture...

, along with the Goldbach conjecture, in Hilbert

David Hilbert

David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...

's list of 23 unsolved problems

Hilbert's problems

Hilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...

, and is also one of the Clay Mathematics Institute

Clay Mathematics Institute

The Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...

Millennium Prize Problems

The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. As of September 2011, six of the problems remain unsolved. A correct solution to any of the problems results in a US$1,000,000 prize being awarded by the institute...

. Since it was formulated, it has withstood concentrated efforts from many outstanding mathematicians. In 1973, Pierre Deligne

Pierre Deligne

- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...

proved an analogue of the Riemann Hypothesis for zeta functions of varieties defined over finite fields. The full version of the hypothesis remains unsolved, although modern computer calculations have shown that the first 10 trillion zeros lie on the critical line.

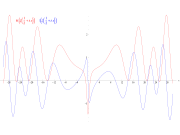
The Riemann zeta function ζ(s) is defined for all complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

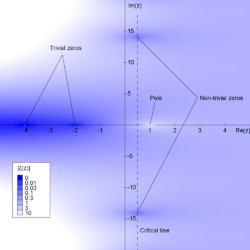
s s ≠ 1. It has zeros at the negative even integers (i.e. at s = −2, −4, −6, ...). These are called the trivial zeros. The Riemann hypothesis is concerned with the non-trivial zeros, and states that:

The real part of any non-trivial zero of the Riemann zeta function is 1/2.

Thus the non-trivial zeros should lie on the critical line, 1/2 + it, where t is a real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

and i is the imaginary unit

Imaginary unit

In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...

.

There are several nontechnical books on the Riemann hypothesis, such as , , ,
. The books , and give mathematical introductions, while
, and are advanced monographs.

The Riemann zeta function

The Riemann zeta function is defined for complex s with real part greater than 1 by the absolutely convergent

Absolute convergence

In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...

infinite series

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

showed that this series equals the Euler product

Euler product

In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...

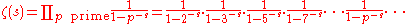
where the infinite product extends over all prime numbers p, and again converges for complex s with real part greater than 1. The convergence of the Euler product shows that ζ(s) has no zeros in this region, as none of the factors have zeros.

The Riemann hypothesis discusses zeros outside the region of convergence of this series, so it needs to be analytically continued

Analytic continuation

In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...

to all complex s. This can be done by expressing it in terms of the Dirichlet eta function as follows. If s is greater than one, then the zeta function satisfies

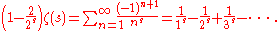
However, the series on the right converges not just when s is greater than one, but more generally whenever s has positive real part. Thus, this alternative series extends the zeta function from to the larger domain .

In the strip the zeta function also satisfies the functional equation

Functional equation

In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...

One may then define ζ(s) for all remaining nonzero complex numbers s by assuming that this equation holds outside the strip as well, and letting ζ(s) equal the right-hand side of the equation whenever s has non-positive real part. If s is a negative even integer then
ζ(s) = 0 because the factor sin(πs/2) vanishes; these are the trivial zeros of the zeta function.
(If s is a positive even integer this argument does not apply because the zeros of sin are cancelled by the poles of the gamma function

Gamma function

In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...

as it takes negative integer arguments.) The value ζ(0) = −1/2 is not determined by the functional equation, but is the limiting value of ζ(s) as s approaches zero. The functional equation also implies that the zeta function has no zeros with negative real part other than the trivial zeros, so all non-trivial zeros lie in the critical strip where s has real part between 0 and 1.

History

In his 1859 paper On the Number of Primes Less Than a Given Magnitude
On the Number of Primes Less Than a Given Magnitude
die Anzahl der Primzahlen unter einer gegebenen is a seminal 8-page paper by Bernhard Riemann published in the November 1859 edition of the Monatsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin.Although it is the only paper he ever published on number theory, it...

Riemann found an explicit formula for the number of primes π(x) less than a given number x. His formula was given in terms of the related function

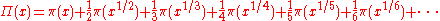
which counts primes where a prime power pⁿ counts as 1/n of a prime. The number of primes can be recovered from this function by

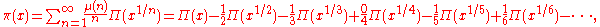
where μ is the Möbius function

Möbius function

The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...

. Riemann's formula is then

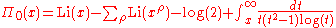
where the sum is over the nontrivial zeros of the zeta function and where Π₀ is a slightly modified version of Π that replaces its value at its points of discontinuity by the average of its upper and lower limits:

The summation in Riemann's formula is not absolutely convergent

Absolute convergence

In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...

, but may be evaluated by taking the zeros ρ in order of the absolute value of their imaginary part. The function Li occurring in the first term is the (unoffset) logarithmic integral function

Logarithmic integral function

In mathematics, the logarithmic integral function or integral logarithm li is a special function. It occurs in problems of physics and has number theoretic significance, occurring in the prime number theorem as an estimate of the number of prime numbers less than a given value.-Integral...

given by the Cauchy principal value

Cauchy principal value

In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...

of the divergent integral

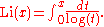
The terms Li(x^ρ) involving the zeros of the zeta function need some care in their definition as Li has branch points at 0 and 1, and are defined (for x > 1) by analytic continuation in the complex variable ρ in the region Re(ρ) > 0, i.e. they should be considered as Ei

Exponential integral

In mathematics, the exponential integral is a special function defined on the complex plane given the symbol Ei.-Definitions:For real, nonzero values of x, the exponential integral Ei can be defined as...

(ρ ln x). The other terms also correspond to zeros: the dominant term Li(x) comes from the pole at s = 1, considered as a zero of multiplicity −1, and the remaining small terms come from the trivial zeros. For some graphs of the sums of the first few terms of this series see or .

This formula says that the zeros of the Riemann zeta function control the oscillations of primes around their "expected" positions. Riemann knew that the non-trivial zeros of the zeta function were symmetrically distributed about the line and he knew that all of its non-trivial zeros must lie in the range He checked that a few of the zeros lay on the critical line with real part 1/2 and suggested that they all do; this is the Riemann hypothesis.

Consequences of the Riemann hypothesis

The practical uses of the Riemann hypothesis include many propositions which
are known to be true under the Riemann hypothesis, and some which can be
shown to be equivalent to the Riemann hypothesis.

Distribution of prime numbers

Riemann's explicit formula for the number of primes less than a given number in terms of a sum over the zeros of the Riemann zeta function says that the magnitude of the oscillations of primes around their expected position is controlled by the real parts of the zeros of the zeta function. In particular the error term in the prime number theorem

Prime number theorem

In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....

is closely related to the position of the zeros: for example, the supremum

Supremum

In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...

of real parts of the zeros is the infimum

Infimum

In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...

of numbers β such that the error is O(x^β) .

Von Koch (1901) proved that the Riemann hypothesis is equivalent to the "best possible" bound for the error of the prime number theorem.

A precise version of Koch's result, due to , says that the Riemann hypothesis is equivalent to

Growth of arithmetic functions

The Riemann hypothesis implies strong bounds on the growth of many other arithmetic functions, in addition to the primes counting function above.

One example involves the Möbius function

Möbius function

The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...

μ. The statement that the equation

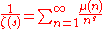
is valid for every s with real part greater than 1/2, with the sum on the right hand side converging, is equivalent to the Riemann hypothesis. From this we can also conclude that if the Mertens function is defined by

then the claim that

for every positive ε is equivalent to the Riemann hypothesis . (For the meaning of these symbols, see Big O notation

Big O notation

In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...

.) The determinant of the order n Redheffer matrix

Redheffer matrix

In mathematics, a Redheffer matrix, studied by , is a matrix whose entries aij are 1 if i divides j or if j = 1; otherwise, aij = 0....

is equal to M(n), so the Riemann hypothesis can also be stated as a condition on the growth of these determinants. The Riemann hypothesis puts a rather tight bound on the growth of M, since disproved the slightly stronger Mertens conjecture

Mertens conjecture

In mathematics, the Mertens conjecture is the incorrect statement that the Mertens function M is bounded by √n, which implies the Riemann hypothesis...

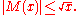
The Riemann hypothesis is equivalent to many other conjectures about the rate of growth of other arithmetic functions aside from μ(n). A typical example is Robin's theorem , which states that if σ(n) is the divisor function

Divisor function

In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...

, given by

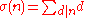
then

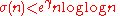
for all n > 5040 if and only if the Riemann hypothesis is true, where γ is the Euler–Mascheroni constant

Euler–Mascheroni constant

The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....

.

Another example was found by showing that the Riemann hypothesis is equivalent to a statement that the terms of the Farey sequence

Farey sequence

In mathematics, the Farey sequence of order n is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size....

are fairly regular. More precisely, if F_n is the Farey sequence of order n, beginning with 1/n and up to 1/1, then the claim that for all ε > 0

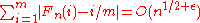
is equivalent to the Riemann hypothesis. Here

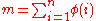is the number of terms in the Farey sequence of order n.

For an example from group theory, if g(n) is Landau's function

Landau's function

In mathematics, Landau's function g, named after Edmund Landau, is defined for every natural number n to be the largest order of an element of the symmetric group Sn...

given by the maximal order of elements of the symmetric group

Symmetric group

In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...

S_n of degree n, then showed that the Riemann hypothesis is equivalent to the bound

for all sufficiently large n.

Lindelöf hypothesis and growth of the zeta function

The Riemann hypothesis has various weaker consequences as well; one is the Lindelöf hypothesis on the rate of growth of the zeta function on the critical line, which says that, for any ε > 0,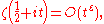

as t tends to infinity.

The Riemann hypothesis also implies quite sharp bounds for the growth rate of the zeta function in other regions of the critical strip. For example, it implies that

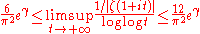
so the growth rate of ζ(1+it) and its inverse would be known up to a factor of 2 .

Large prime gap conjecture

The prime number theorem implies that on average, the gap between the prime p and its successor is log p. However, some gaps between primes may be much larger than the average. Cramér

Harald Cramér

Harald Cramér was a Swedish mathematician, actuary, and statistician, specializing in mathematical statistics and probabilistic number theory. He was once described by John Kingman as "one of the giants of statistical theory".-Early life:Harald Cramér was born in Stockholm, Sweden on September...

proved that, assuming the Riemann hypothesis, every gap is O(√p log p). This is a case when even the best bound that can currently be proved using the Riemann hypothesis is far weaker than what seems to be true: Cramér's conjecture implies that every gap is O((log p)²) which, while larger than the average gap, is far smaller than the bound implied by the Riemann hypothesis. Numerical evidence supports Cramér's conjecture .

Criteria equivalent to the Riemann hypothesis

Many statements equivalent to the Riemann hypothesis have been found, though so far none of them have led to
much progress in solving it. Some typical examples are as follows. (Others involve the divisor function σ(n).)

The Riesz criterion was given by , to the effect that the bound

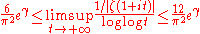
holds for all

if and only if the Riemann hypothesis holds.

proved that the Riemann Hypothesis is true if and only if
the space of functions of the form

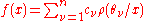
where ρ(z) is the fractional part of z, , and

,
is dense in the Hilbert space L²(0,1) of square-integrable functions on the unit interval.
extended this by showing that the zeta function has no zeros with real part greater than 1/p if and only if this function space is dense in L^p(0,1)

showed that the Riemann hypothesis is true if and only if the integral equation

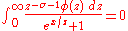
has no non-trivial bounded solutions φ for 1/2<σ<1.

Weil's criterion

Weil's criterion

In mathematics, Weil's criterion is a criterion of André Weil for the Generalized Riemann Hypothesis to be true. It takes the form of an equivalent statement, to the effect that a certain generalized function is positive definite....

is the statement that the positivity of a certain function is equivalent to the Riemann hypothesis. Related is Li's criterion

Li's criterion

In number theory, Li's criterion is a particular statement about the positivity of a certain sequence that is completely equivalent to the Riemann hypothesis. The criterion is named after Xian-Jin Li, who presented it in 1997. Recently, Enrico Bombieri and Jeffrey C...

, a statement that the positivity of a certain sequence of numbers is equivalent to the Riemann hypothesis.

proved that the Riemann hypothesis is equivalent to the statement that

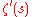, the derivative of

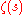, has no zeros in the strip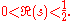

That ζ has only simple zeros on the critical line is equivalent (by definition) to its derivative having no zeros on the critical line.

Consequences of the generalized Riemann hypothesis

Several applications use the generalized Riemann hypothesis for Dirichlet L-series or zeta functions of number fields rather than just the Riemann hypothesis. Many basic properties of the Riemann zeta function can easily be generalized to all Dirichlet L-series, so it is plausible that a method that proves the Riemann hypothesis for the Riemann zeta function would also work for the generalized Riemann hypothesis for Dirichlet L-functions. Several results first proved using the generalized Riemann hypothesis were later given unconditional proofs without using it, though these were usually much harder. Many of the consequences on the following list are taken from .

In 1913, Gronwall showed that the generalized Riemann hypothesis implies that Gauss's list of imaginary quadratic fields with class number 1 is complete, though Baker, Stark and Heegner later gave unconditional proofs of this without using the generalized Riemann hypothesis.
In 1917, Hardy and Littlewood showed that the generalized Riemann hypothesis implies a conjecture of Chebyshev that

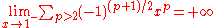
which says that in some sense primes 3 mod 4 are more common than primes 1 mod 4.

In 1923 Hardy and Littlewood showed that the generalized Riemann hypothesis implies a weak form of the Goldbach conjecture for odd numbers: that every sufficiently large odd number is the sum of 3 primes, though in 1937 Vinogradov gave an unconditional proof. In 1997 Deshouillers, Effinger, te Riele, and Zinoviev showed that the generalized Riemann hypothesis implies that every odd number greater than 5 is the sum of 3 primes.
In 1934, Chowla showed that the generalized Riemann hypothesis implies that the first prime in the arithmetic progression a mod m is at most Km²log(m)² for some fixed constant K.
In 1967, Hooley showed that the generalized Riemann hypothesis implies Artin's conjecture on primitive roots
Artin's conjecture on primitive roots
In number theory, Artin's conjecture on primitive roots states that a given integer a which is not a perfect square and not −1 is a primitive root modulo infinitely many primes p. The conjecture also ascribes an asymptotic density to these primes...

.
In 1973, Weinberger showed that the generalized Riemann hypothesis implies that Euler's list of idoneal number
Idoneal number
In mathematics, Euler's idoneal numbers, , are the positive integers D such that any integer expressible in only one way as x2 ± Dy2 is a prime, prime power, or twice one of these.A positive integer n is idoneal if and only if it cannot be written as...

s is complete. showed that the generalized Riemann hypothesis for the zeta functions of all algebraic number fields implies that any number field with class number 1 is either Euclidean
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...

or an imaginary quadratic number field of discriminant −19, −43, −67, or −163.
In 1976, G. Miller showed that the generalized Riemann hypothesis implies that one can test if a number is prime in polynomial times. In 2002, Manindra Agrawal, Neeraj Kayal and Nitin Saxena proved this result unconditionally using the AKS primality test
AKS primality test
The AKS primality test is a deterministic primality-proving algorithm created and published by three Indian Institute of Technology Kanpur computer scientists, Manindra Agrawal, Neeraj Kayal, and Nitin Saxena, on August 6, 2002, in a paper titled "PRIMES is in P"...

. discussed how the generalized Riemann hypothesis can be used to give sharper estimates for discriminants and class numbers of number fields. showed that the generalized Riemann hypothesis implies that Ramanujan's integral quadratic form x² +y² + 10z² represents all integers that it represents locally, with exactly 18 exceptions.

Dirichlet L-series and other number fields

The Riemann hypothesis can be generalized by replacing the Riemann zeta function by the formally similar, but much more general, global L-function

L-function

The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...

s. In this broader setting, one expects the non-trivial zeros of the global L-functions to have real part 1/2. It is these conjectures, rather than the classical Riemann hypothesis only for the single Riemann zeta function, which accounts for the true importance of the Riemann hypothesis in mathematics.

The generalized Riemann hypothesis

Generalized Riemann hypothesis

The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...

extends the Riemann hypothesis to all Dirichlet L-functions.
In particular it implies the conjecture that Siegel zero

Siegel zero

In mathematics, more specifically in the field of analytic number theory, a Siegel zero, named after Carl Ludwig Siegel, is a type of potential counterexample to the generalized Riemann hypothesis, on the zeroes of Dirichlet L-function....

s (zeros of L functions between 1/2 and 1) do not exist.

The extended Riemann hypothesis extends the Riemann hypothesis to all Dedekind zeta function

Dedekind zeta function

In mathematics, the Dedekind zeta function of an algebraic number field K, generally denoted ζK, is a generalization of the Riemann zeta function—which is obtained by specializing to the case where K is the rational numbers Q...

s of algebraic number field

Algebraic number field

In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...

s. The extended Riemann hypothesis for abelian extension of the rationals is equivalent to the generalized Riemann hypothesis. The Riemann hypothesis can also be extended to the L-functions of Hecke character

Hecke character

In number theory, a Hecke character is a generalisation of a Dirichlet character, introduced by Erich Hecke to construct a class ofL-functions larger than Dirichlet L-functions, and a natural setting for the Dedekind zeta-functions and certain others which have functional equations analogous to...

s of number fields.

The grand Riemann hypothesis

Grand Riemann hypothesis

In mathematics, the grand Riemann hypothesis is a generalisation of the Riemann hypothesis and Generalized Riemann hypothesis. It states that the nontrivial zeros of all automorphic L-functions lie on the critical line...

extends it to all automorphic zeta functions, such as Mellin transform

Mellin transform

In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...

s of Hecke eigenforms.

Function fields and zeta functions of varieties over finite fields

introduced global zeta functions of (quadratic) function fields

Function field of an algebraic variety

In algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...

and conjectured an analogue of the Riemann hypothesis for them, which has been proven by Hasse in the genus 1 case and by in general. For instance, the fact that the Gauss sum

Quadratic Gauss sum

In number theory, quadratic Gauss sums are certain finite sums of roots of unity. A quadratic Gauss sum can be interpreted as a linear combination of the values of the complex exponential function with coefficients given by a quadratic character; for a general character, one obtains a more general...

, of the quadratic character of a finite field

Finite field

In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...

of size q (with q odd), has absolute value

is actually an instance of the Riemann hypothesis in the function field setting. This led to conjecture a similar statement for all algebraic varieties

Algebraic variety

In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...

; the resulting Weil conjectures

Weil conjectures

In mathematics, the Weil conjectures were some highly-influential proposals by on the generating functions derived from counting the number of points on algebraic varieties over finite fields....

were proven by .

Selberg zeta functions

introduced the Selberg zeta function of a Riemann surface. These are similar to the Riemann zeta function: they have a functional equation, and an infinite product similar to the Euler product but taken over closed geodesics rather than primes. The Selberg trace formula

Selberg trace formula

In mathematics, the Selberg trace formula, introduced by , is an expression for the character of the unitary representation of G on the space L2 of square-integrable functions, where G is a Lie group and Γ a cofinite discrete group...

is the analogue for these functions of the explicit formulas in prime number theory. Selberg proved that the Selberg zeta functions satisfy the analogue of the Riemann hypothesis, with the imaginary parts of their zeros related to the eigenvalues of the Laplacian operator of the Riemann surface.

Ihara zeta functions

The Ihara zeta function

Ihara zeta function

The Ihara zeta-function is a zeta function associated with a finite graph. It closely resembles the Selberg zeta-function, and is used to relate closed paths to the spectrum of the adjacency matrix. The Ihara zeta-function was first defined by Yasutaka Ihara in the 1960s in the context of discrete...

of a finite graph is an analogue of the Selberg zeta function introduced by Yasutaka Ihara. A regular finite graph is a Ramanujan graph

Ramanujan graph

A Ramanujan graph, named after Srinivasa Ramanujan, is a regular graph whose spectral gap is almost as large as possible . Such graphs are excellent spectral expanders....

, a mathematical model of efficient communication networks, if and only if its Ihara zeta function satisfies the analogue of the Riemann hypothesis as was pointed out by T. Sunada

Toshikazu Sunada

is a Japanese mathematician and author of many books and essays on mathematics and mathematical sciences. He is professor of mathematics at Meiji University, Tokyo, and is also professor emeritus of Tohoku University, Tohoku, Japan...

Montgomery's pair correlation conjecture

suggested the pair correlation conjecture that the correlation functions of the (suitably normalized) zeros of the zeta function should be the same as those of the eigenvalues of a random hermitian matrix. showed that this is supported by large scale numerical calculations of these correlation functions.

Montgomery showed that (assuming the Riemann hypothesis) at least 2/3 of all zeros are simple, and a related conjecture is that all zeros of the zeta function are simple (or more generally have no non-trivial integer linear relations between their imaginary parts). Dedekind zeta function

Dedekind zeta function

s of algebraic number fields, which generalize the Riemann zeta function, often do have multiple complex zeros. This is because the Dedekind zeta functions factorize as a product of powers of Artin L-function

Artin L-function

In mathematics, an Artin L-function is a type of Dirichlet series associated to a linear representation ρ of a Galois group G. These functions were introduced in the 1923 by Emil Artin, in connection with his research into class field theory. Their fundamental properties, in particular the Artin...

s, so zeros of Artin L-functions sometimes give rise to multiple zeros of Dedekind zeta functions. Other examples of zeta functions with multiple zeros are the L-functions of some elliptic curve

Elliptic curve

In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...

s: these can have multiple zeros at the real point of their critical line; the Birch-Swinnerton-Dyer conjecture predicts that the multiplicity of this zero is the rank of the elliptic curve.

Other zeta functions

There are many other examples of zeta functions with analogues of the Riemann hypothesis,
some of which have been proved. Goss zeta function

Goss zeta function

In the field of mathematics, the Goss zeta function, named after David Goss, is an analogue of the Riemann zeta function for function fields. proved that it satisfies an analogue of the Riemann hypothesis....

s of function fields have a Riemann hypothesis, proved by .
The main conjecture of Iwasawa theory

Iwasawa theory

In number theory, Iwasawa theory is the study of objects of arithmetic interest over infinite towers of number fields. It began as a Galois module theory of ideal class groups, initiated by Kenkichi Iwasawa, in the 1950s, as part of the theory of cyclotomic fields. In the early 1970s, Barry Mazur...

, proved by Barry Mazur

Barry Mazur

-Life:Born in New York City, Mazur attended the Bronx High School of Science and MIT, although he did not graduate from the latter on account of failing a then-present ROTC requirement. Regardless, he was accepted for graduate school and received his Ph.D. from Princeton University in 1959,...

and Andrew Wiles

Andrew Wiles

Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...

for cyclotomic field

Cyclotomic field

In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...

s, and Wiles for totally real fields

Totally real number field

In number theory, a number field K is called totally real if for each embedding of K into the complex numbers the image lies inside the real numbers...

, identifies the zeros of a p-adic L-function with the eigenvalues of an operator, so can be thought of as an analogue of the Hilbert–Pólya conjecture for p-adic L-functions

P-adic L-function

In mathematics, a p-adic zeta function, or more generally a p-adic L-function, is a function analogous to the Riemann zeta function, or more general L-functions, but whose domain and target are p-adic...

Attempts to prove the Riemann hypothesis

Several mathematicians have addressed the Riemann hypothesis, but none of their attempts have yet been accepted as correct solutions.
lists some incorrect solutions, and more are frequently announced.

Operator theory

Hilbert and Polya suggested that one way to derive the Riemann hypothesis would be to find a self-adjoint operator

Self-adjoint operator

In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...

, from the existence of which the statement on the real parts of the zeros of ζ(s) would follow when one applies the criterion on real eigenvalues. Some support for this idea comes from several analogues of the Riemann zeta functions whose zeros correspond to eigenvalues of some operator: the zeros of a zeta function of a variety over a finite field correspond to eigenvalues of a Frobenius element on an étale cohomology

Étale cohomology

In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...

group, the zeros of a Selberg zeta function are eigenvalues of a Laplacian operator of a Riemann surface, and the zeros of a p-adic zeta function correspond to eigenvectors of a Galois action on ideal class group

Ideal class group

In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...

s.

showed that the distribution of the zeros of the Riemann zeta function shares some statistical properties with the eigenvalues of random matrices drawn from the Gaussian unitary ensemble. This gives some support to the Hilbert–Pólya conjecture.

In 1999, Michael Berry and Jon Keating conjectured that there is some unknown quantization

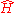of the classical Hamiltonian

so that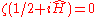

and even more strongly, that the Riemann zeros coincide with the spectrum of the operator

. This is to be contrasted to canonical quantization

Canonical quantization

In physics, canonical quantization is a procedure for quantizing a classical theory while attempting to preserve the formal structure of the classical theory, to the extent possible. Historically, this was Werner Heisenberg's route to obtaining quantum mechanics...

which leads to the Heisenberg uncertainty principle

and the natural numbers as spectrum of the quantum harmonic oscillator

Quantum harmonic oscillator

The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...

. The crucial point is that the Hamiltonian should be a self-adjoint operator so that the quantization would be a realization of the Hilbert–Pólya program. In a connection with this quantum mechanical problem Berry and Connes had proposed that the inverse of the potential of the Hamiltonian is connected to the half-derivative of the function

then, in Berry–Connes approach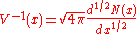

. This yields to a Hamiltonian whose eigenvalues are the square of the imaginary part of the Riemann zeros, also the functional determinant of this Hamiltonian operator is just the Riemann Xi function

Riemann Xi function

In mathematics, the Riemann Xi function is a variant of the Riemann zeta function, and is defined so as to have a particularly simple functional equation...

The analogy with the Riemann hypothesis over finite fields suggests that the Hilbert space
containing eigenvectors corresponding to the zeros might be some sort of first cohomology group of the spectrum

Spectrum of a ring

In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...

Spec(Z) of the integers. described some of the attempts to find such a cohomology theory.

constructed a natural space of invariant functions on the upper half plane which has eigenvalues under the Laplacian operator corresponding to zeros of the Riemann zeta function, and remarked that in the unlikely event that one could show the existence of a suitable positive definite inner product on this space the Riemann hypothesis would follow. discussed a related example, where due to a bizarre bug a computer program listed zeros of the Riemann zeta function as eigenvalues of the same Laplacian operator.

surveyed some of the attempts to construct a suitable physical model related to the Riemann zeta function.

Lee–Yang theorem

The Lee–Yang theorem

Lee–Yang theorem

In statistical mechanics, the Lee–Yang theorem states that if partition functions of certain models in statistical field theory with ferromagnetic interactions are considered as functions of an external field, then all zeros...

states that the zeros of certain partition functions in statistical mechanics all lie on
a "critical line" with real part 0, and this has led to some speculation about a relationship with the Riemann hypothesis .

Turán's result

showed that if the functions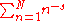

have no zeros when the real part of s is greater than one then

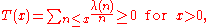
where λ(n) is the Liouville function given by (−1)^r if n has r prime factors.
He showed that this in turn would imply that the Riemann hypothesis is true. However proved that T(x) is negative for infinitely many x (and also disproved the closely related Pólya conjecture

Pólya conjecture

In number theory, the Pólya conjecture stated that 'most' of the natural numbers less than any given number have an odd number of prime factors. The conjecture was posited by the Hungarian mathematician George Pólya in 1919, and proved false in 1958...

), and showed that the smallest such x is . showed by numerical calculation that the finite Dirichlet series above for N=19 has a zero with real part greater than 1. Turán also showed that a somewhat weaker assumption, the nonexistence of zeros with real part greater than 1+N^−1/2+ε for large N in the finite Dirichlet series above, would also imply the Riemann hypothesis, but showed that for all sufficiently large N these series have zeros with real part greater than . Therefore, Turán's result is vacuously true

Vacuous truth

A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...

and cannot be used to help prove the Riemann hypothesis.

Noncommutative geometry

has described a relationship between the Riemann hypothesis and noncommutative geometry

Noncommutative geometry

Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...

, and shows that a suitable analogue of the Selberg trace formula

Selberg trace formula

for the action of the idèle class group on the adèle class space would imply the Riemann hypothesis. Some of these ideas are elaborated in .

Hilbert spaces of entire functions

showed that the Riemann hypothesis would follow from a positivity condition on a certain Hilbert space of entire functions.
However showed that the necessary positivity conditions are not satisfied.

Quasicrystals

The Riemann hypothesis implies that the zeros of the zeta function form a quasicrystal

Quasicrystal

A quasiperiodic crystal, or, in short, quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry...

, meaning a distribution with discrete support whose Fourier transform also has discrete support.
suggested trying to prove the Riemann hypothesis by classifying, or at least studying, 1-dimensional quasicrystals.

Multiple zeta functions

Deligne's proof of the Riemann hypothesis over finite fields used the zeta functions of product varieties, whose zeros and poles correspond to sums of zeros and poles of the original zeta function, in order to bound the real parts of the zeros of the original zeta function. By analogy,
introduced multiple zeta functions whose zeros and poles correspond to sums of zeros and poles of the Riemann zeta function. To make the series converge he restricted to sums of zeros or poles all with non-negative imaginary part. So far, the known bounds on the zeros and poles of the multiple zeta functions are not strong enough to give useful estimates for the zeros of the Riemann zeta function.

Number of zeros

The functional equation combined with the argument principle

Argument principle

In complex analysis, the argument principle determines the difference between the number of zeros and poles of a meromorphic function by computing a contour integral of the function's logarithmic derivative....

implies that the number of zeros of the zeta function with imaginary part between 0 and T is given by

for s=1/2+iT, where the argument is defined by varying it continuously along the line with Im(s)=T,
starting with argument 0 at ∞+iT.
This is the sum of a large but well understood term

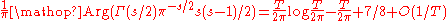
and a small but rather mysterious term

So the density of zeros with imaginary part near T is about log(T)/2π, and the function S describes the small deviations from this. The function S(t) jumps by 1 at each zero of the zeta function, and for it decreases monotonically between zeros with derivative close to −log t.

Karatsuba

Anatolii Alexeevitch Karatsuba

Anatolii Alexeevitch Karatsuba was a Russian mathematician, who authored the first fast multiplication method: the Karatsuba algorithm, a fast procedure for multiplying large numbers.- Studies and work :...

(1996) proved that every interval

for

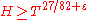contains at least

points where the function

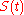changes sign.

showed that the average moments of even powers of S are given by

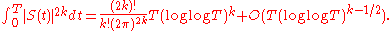
This suggests that S(T)/(log log T)^1/2 resembles
a Gaussian random variable with mean 0 and variance 2π² ( proved this fact).
In particular |S(T)| is usually somewhere around (log log T)^1/2, but occasionally much larger. The exact order of growth of S(T) is not known. There has been no unconditional improvement to Riemann's original bound S(T)=O(log T), though the Riemann hypothesis implies the slightly smaller bound S(T)=O(log T/log log T) . The true order of magnitude may be somewhat less than this, as
random functions with the same distribution as S(T) tend to have
growth of order about log(T)^1/2. In the other direction it cannot be too small: showed that , and assuming the Riemann hypothesis Montgomery showed that
.

Numerical calculations confirm that S grows very slowly: |S(T)| < 1 for , |S(T)| < 2 for T < , and the largest value of |S(T)| found so far is not much larger than 3 .

Riemann's estimate S(T) = O(log T) implies that the gaps between zeros are bounded, and Littlewood improved this slightly, showing that the gaps between their imaginary parts tends to 0.

The theorem of Hadamard and de la Vallée-Poussin

and independently proved that no zeros could lie on the line Re(s) = 1. Together with the functional equation and the fact that there are no zeros with real part greater than 1, this showed that all non-trivial zeros must lie in the interior of the critical strip . This was a key step in their first proofs of the prime number theorem

Prime number theorem

.

Both the original proofs that the zeta function has no zeros with real part 1 are similar, and depend on showing that
if ζ(1+it) vanishes, then ζ(1+2it) is singular, which is not possible. One way of doing this is by using the
inequality

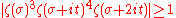for σ>1, t real,
and looking at the limit as σ tends to 1.
This inequality follows by taking the real part of the log of the Euler product to see that

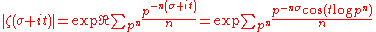
(where the sum is over all prime powers pⁿ)
so that

which is at least 1 because all the terms in the sum are positive, due to the inequality

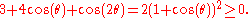
Zero-free regions

De la Vallée-Poussin (1899-1900) proved that if σ+it is a zero of the Riemann zeta function, then 1-σ ≥ C/log(t) for some positive constant C. In other words zeros cannot be too close to the line σ=1: there is a zero-free region close to this line. This zero-free region has been enlarged by several authors.
gave a version with explicit numerical constants: whenever |t| ≥ 3 and

Zeros on the critical line

and showed there are infinitely many zeros on the critical line, by considering moments of certain functions related to the zeta function. proved that at least a (small) positive proportion of zeros lie on the line. improved this to one-third of the zeros by relating the zeros of the zeta function to those of its derivative, and improved this further to two-fifths.

Most zeros lie close to the critical line. More precisely, showed that for any positive ε, all but an infinitely small proportion of zeros lie within a distance ε of the critical line. gives several more precise versions of this result, called zero density estimates, which bound the number of zeros in regions with imaginary part at most T and real part at least 1/2+ε.

The Hardy–Littlewood conjectures

In 1914 Godfrey Harold Hardy

G. H. Hardy

Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....

proved that

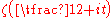has infinitely many real zeros.

Let

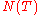be the total number of real zeros,

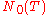be the total number of zeros of odd order of the function

, lying on the interval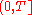

.

The next two conjectures of Hardy

G. H. Hardy

Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....

and John Edensor Littlewood

John Edensor Littlewood

John Edensor Littlewood was a British mathematician, best known for the results achieved in collaboration with G. H. Hardy.-Life:...

on the distance between real zeros of

and on the density of zeros of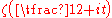

on intervals

for sufficiently great

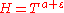and with as less as possible value of

, where

is an arbitrarily small number, open two new directions in the investigation of the Riemann zeta function:

1. for any

there exists

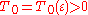such that for

and

the interval

contains a zero of odd order of the function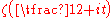

.

2. for any

there exist

and

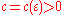, such that for

and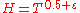

the inequality

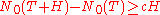is true.

The Selberg conjecture

investigated the problem of Hardy–Littlewood 2 and proved that for any

there exists such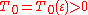

and

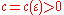, such that for

and

the inequality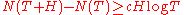

is true. Selberg conjectured that this could be tightened to

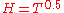. proved that for a fixed

satisfying the condition

, a sufficiently large

and

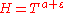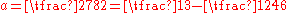, the interval

contains at least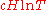

real zeros of the Riemann zeta function

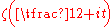and therefore confirmed the Selberg conjecture. The estimates of Selberg and Karatsuba can not be improved in respect of the order of growth as

.

proved that an analog of the Selberg conjecture holds for almost all intervals

, where

is an arbitrarily small fixed positive number. The Karatsuba method permits to investigate zeros of the Riemann zeta-function on "supershort" intervals of the critical line, that is, on the intervals

, the length

of which grows slower than any, even arbitrarily small degree

. In particular, he proved that for any given numbers

satisfying the conditions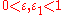

almost all intervals

for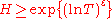

contain at least

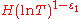zeros of the function

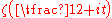. This estimate is quite close to the one that follows from the Riemann hypothesis.

Numerical calculations

The function

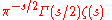
has the same zeros as the zeta function in the critical strip, and is real on the critical line because of the functional equation, so one can prove the existence of zeros exactly on the real line between two points by checking numerically that the function has opposite signs at these points. Usually one writes

where Hardy's function Z

Z function

In mathematics, the Z-function is a function used for studying theRiemann zeta-function along the critical line where the real part of theargument is one-half.It is also called the Riemann-Siegel Z-function,the Riemann-Siegel zeta-function,...

and the Rieman–Siegel theta function θ are uniquely defined by this and the condition that they are smooth real functions with θ(0)=0.
By finding many intervals where the function Z changes sign one can show that there are many zeros on the critical line.
To verify the Riemann hypothesis up to a given imaginary part T of the zeros, one also has to check that there are no further zeros off the line in this region. This can be done by calculating the total number of zeros in the region and checking that it is the same as the number of zeros found on the line. This allows one to verify the Riemann hypothesis computationally up to any desired value of T (provided all the zeros of the zeta function in this region are simple and on the critical line).

Some calculations of zeros of the zeta function are listed below. So far all zeros that have been checked are on the critical line and are simple. (A multiple zero would cause problems for the zero finding algorithms, which depend on finding sign changes between zeros.) For tables of the zeros, see or .

Year	Number of zeros	Author
1859?	3	B. Riemann used the Riemann–Siegel formula Riemann–Siegel formula In mathematics, the Riemann–Siegel formula is an asymptotic formula for the error of the approximate functional equation of the Riemann zeta function, an approximation of the zeta function by a sum of two finite Dirichlet series. It was found by in unpublished manuscripts of Bernhard Riemann... (unpublished, but reported in ).
1903	15	J. P. used Euler–Maclaurin summation and discovered Gram's law. He showed that all 10 zeros with imaginary part at most 50 range lie on the critical line with real part 1/2 by computing the sum of the inverse 10th powers of the roots he found.
1914	79 (γ_n ≤ 200)	R. J. introduced a better method of checking all the zeros up to that point are on the line, by studying the argument S(T) of the zeta function.
1925	138 (γ_n ≤ 300)	J. I. found the first failure of Gram's law, at the Gram point g₁₂₆.
1935	195	E. C. used the recently rediscovered Riemann–Siegel formula Riemann–Siegel formula In mathematics, the Riemann–Siegel formula is an asymptotic formula for the error of the approximate functional equation of the Riemann zeta function, an approximation of the zeta function by a sum of two finite Dirichlet series. It was found by in unpublished manuscripts of Bernhard Riemann... , which is much faster than Euler–Maclaurin summation.It takes about O(T^3/2+ε) steps to check zeros with imaginary part less than T, while the Euler–Maclaurin method takes about O(T^2+ε) steps.
1936	1041	E. C. and L. J. Comrie were the last to find zeros by hand.
1953	1104	A. M. found a more efficient way to check that all zeros up to some point are accounted for by the zeros on the line, by checking that Z has the correct sign at several consecutive Gram points and using the fact that S(T) has average value 0. This requires almost no extra work because the sign of Z at Gram points is already known from finding the zeros, and is still the usual method used. This was the first use of a digital computer to calculate the zeros.
1956		D. H. discovered a few cases where the zeta function has zeros that are "only just" on the line: two zeros of the zeta function are so close together that it is unusually difficult to find a sign change between them. This is called "Lehmer's phenomenon", and first occurs at the zeros with imaginary parts 7005.063 and 7005.101, which differ by only .04 while the average gap between other zeros near this point is about 1.
1956		D. H. Lehmer
1958		N. A. Meller
1966		R. S. Lehman
1968		stated Rosser's rule (described below).
1977		R. P. Brent Richard Brent (scientist) Richard Peirce Brent is an Australian mathematician and computer scientist, born in 1946. He holds the position of Distinguished Professor of Mathematics and Computer Science with a joint appointment in the Mathematical Sciences Institute and the College of Engineering and Computer Science at...
1979		R. P. Brent
1982		R. P. Brent, J. van de Lune, H. J. J. te Riele, D. T. Winter
1983		J. van de Lune, H. J. J. te Riele
1986		gave some statistical data about the zeros and give several graphs of Z at places where it has unusual behavior.
1987	A few of large (~10¹²) height	computed smaller numbers of zeros of much larger height, around 10¹², to high precision to check Montgomery's pair correlation conjecture.
1992	A few of large (~10²⁰) height	computed a 175 million zeroes of heights around 10²⁰ and a few more of heights around 2, and gave an extensive discussion of the results.
1998	10000 of large (~10²¹) height	computed some zeros of height about 10²¹
2001		J. van de Lune (unpublished)
2004		S. Wedeniwski (ZetaGrid ZetaGrid ZetaGrid was at one time the largest distributed computing project designed to explore roots of the Riemann zeta function, checking over one billion roots a day.... distributed computing)
2004	and a few of large (up to ~10²⁴) heights	X. and Patrick Demichel used the Odlyzko–Schönhage algorithm. They also checked two billion zeros around heights 10¹³, 10¹⁴, ... , 10²⁴.

Gram points

A Gram point is a value of t such that ζ(1/2 + it) = Z(t)e^− iθ(t) is a non-zero real; these are easy to find because they are the points where the Euler factor at infinity π^−s/2Γ(s/2) is real at s = 1/2 + it, or equivalently θ(t) is a multiple nπ of π.
They are usually numbered as g_n for n = −1, 0, 1, ..., where g_n is the unique solution of θ(t) = nπ with t ≥ 8 (θ is increasing beyond this point; there is a second point with θ(t) = −π near 3.4, and θ(0) = 0).
Gram observed that there was often exactly one zero of the zeta function between any two Gram points; Hutchinson called this observation Gram's law. There are several other closely related statements that are also sometimes called Gram's law: for example, (−1)ⁿZ(g_n) is usually positive, or Z(t) usually has opposite sign at consecutive Gram points. The imaginary parts γ_n of the first few zeros (in blue) and the first few Gram points g_n are given in the following table

		g₋₁	γ₁	g₀	γ₂	g₁	γ₃	g₂	γ₄	g₃	γ₅	g₄	γ₆	g₅
0	3.4	9.667	14.135	17.846	21.022	23.170	25.011	27.670	30.425	31.718	32.935	35.467	37.586	38.999

The first failure of Gram's law occurs at the 127'th zero and the Gram point g₁₂₆, which are in the "wrong" order.

g₁₂₄	γ₁₂₆	g₁₂₅	g₁₂₆	γ₁₂₇	γ₁₂₈	g₁₂₇	γ₁₂₉	g₁₂₈
279.148	279.229	280.802	282.455	282.465	283.211	284.104	284.836	285.752

A Gram point t is called good if the zeta function is positive at 1/2 + it. The indices of the "bad" Gram points where Z has the "wrong" sign are 126, 134, 195, 211,... . A Gram block is an interval bounded by two good Gram points such that all the Gram points between them are bad. A refinement of Gram's law called Rosser's rule due to says that Gram blocks often have the expected number of zeros in them (the same as the number of Gram intervals), even though some of the individual Gram intervals in the block may not have exactly one zero in them. For example, the interval bounded by g₁₂₅ and g₁₂₇ is a Gram block containing a unique bad Gram point g₁₂₆, and contains the expected number 2 of zeros although neither of its two Gram intervals contains a unique zero. Rosser et al. checked that there were no exceptions to Rosser's rule in the first 3 million zeros, although there are infinitely many exceptions to Rosser's rule over the entire zeta function.

Gram's rule and Rosser's rule both say that in some sense zeros do not stray too far from their expected positions. The distance of a zero from its expected position is controlled by the function S defined above, which grows extremely slowly: its average value is of the order of (log log T)^1/2, which only reaches 2 for T around 10²⁴. This means that both rules hold most of the time for small T but eventually break down often.

Arguments for and against the Riemann hypothesis

Mathematical papers about the Riemann hypothesis tend to be cautiously noncommittal about its truth. Of authors who express an opinion, most of them, such as or , imply that they expect (or at least hope) that it is true. The few authors who express serious doubt about it include who lists some reasons for being skeptical, and who flatly states that he believes it to be false, and that there is no evidence whatever for it and no imaginable reason for it to be true. The consensus of the survey articles is that the evidence for it is strong but not overwhelming, so that while it is probably true there is some reasonable doubt about it.

Some of the arguments for (or against) the Riemann hypothesis are listed by , , and , and include the following reasons.

Several analogues of the Riemann hypothesis have already been proved. The proof of the Riemann hypothesis for varieties over finite fields by is possibly the single strongest theoretical reason in favor of the Riemann hypothesis. This provides some evidence for the more general conjecture that all zeta functions associated with automorphic forms satisfy a Riemann hypothesis, which includes the classical Riemann hypothesis as a special case. Similarly Selberg zeta functions satisfy the analogue of the Riemann hypothesis, and are in some ways similar to the Riemann zeta function, having a functional equation and an infinite product expansion analogous to the Euler product expansion. However there are also some major differences; for example they are not given by Dirichlet series. The Riemann hypothesis for the Goss zeta function
Goss zeta function
In the field of mathematics, the Goss zeta function, named after David Goss, is an analogue of the Riemann zeta function for function fields. proved that it satisfies an analogue of the Riemann hypothesis....

was proved by . In contrast to these positive examples, however, some Epstein zeta functions do not satisfy the Riemann hypothesis, even though they have an infinite number of zeros on the critical line . These functions are quite similar to the Riemann zeta function, and have a Dirichlet series expansion and a functional equation, but the ones known to fail the Riemann hypothesis do not have an Euler product and are not directly related to automorphic representations.
The numerical verification that many zeros lie on the line seems at first sight to be strong evidence for it. However analytic number theory has had many conjectures supported by large amounts of numerical evidence that turn out to be false. See Skewes number for a notorious example, where the first exception to a plausible conjecture related to the Riemann hypothesis probably occurs around 10³¹⁶; a counterexample to the Riemann hypothesis with imaginary part this size would be far beyond anything that can currently be computed. The problem is that the behavior is often influenced by very slowly increasing functions such as log log T, that tend to infinity, but do so so slowly that this cannot be detected by computation. Such functions occur in the theory of the zeta function controlling the behavior of its zeros; for example the function S(T) above has average size around (log log T)^1/2 . As S(T) jumps by at least 2 at any counterexample to the Riemann hypothesis, one might expect any counterexamples to the Riemann hypothesis to start appearing only when S(T) becomes large. It is never much more than 3 as far as it has been calculated, but is known to be unbounded, suggesting that calculations may not have yet reached the region of typical behavior of the zeta function.
Denjoy
Arnaud Denjoy
Arnaud Denjoy was a French mathematician.Denjoy was born in Auch, Gers. His contributions include work in harmonic analysis and differential equations. His integral was the first to be able to integrate all derivatives...

's probabilistic argument for the Riemann hypothesis is based on the observation that if μ(x) is a random sequence of "1"s and "−1"s then, for every , the partial sums

satisfy the bound

with probability 1

Almost surely

In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...

. The Riemann hypothesis is equivalent to this bound for the Möbius function

Möbius function

The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...

μ and the Mertens function M derived in the same way from it. In other words, the Riemann hypothesis is in some sense equivalent to saying that μ(x) behaves like a random sequence of coin tosses. When μ(x) is non-zero its sign gives the parity of the number of prime factors of x, so informally the Riemann hypothesis says that the parity of the number of prime factors of an integer behaves randomly. Such probabilistic arguments in number theory often give the right answer, but tend to be very hard to make rigorous, and occasionally give the wrong answer for some results, such as Maier's theorem

Maier's theorem

In number theory, Maier's theorem is a theorem about the numbers of primes in short intervals for which the Cramér's probabilistic model of primes gives the wrong answer.It states that if π is the prime counting function and λ is greater than 1 then...

The calculations in show that the zeros of the zeta function behave very much like the eigenvalues of a random Hermitian matrix, suggesting that they are the eigenvalues of some self-adjoint operator, which would imply the Riemann hypothesis. However all attempts to find such an operator have failed.
There are several theorems, such as Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...

for sufficiently large odd numbers, that were first proved using the generalized Riemann hypothesis, and later shown to be true unconditionally. This could be considered as weak evidence for the generalized Riemann hypothesis, as several of its "predictions" turned out to be true.
Lehmer's phenomenon where two zeros are sometimes very close is sometimes given as a reason to disbelieve in the Riemann hypothesis. However one would expect this to happen occasionally just by chance even if the Riemann hypothesis were true, and Odlyzko's calculations suggest that nearby pairs of zeros occur just as often as predicted by Montgomery's conjecture. suggests that the most compelling reason for the Riemann hypothesis for most mathematicians is the hope that primes are distributed as regularly as possible.

External links

American institute of mathematics
American Institute of Mathematics
The American Institute of Mathematics was founded in 1994 by John Fry and is located in Palo Alto, California. Privately funded by Fry at inception, in 2002, AIM became one of eight NSF-funded mathematical institutes....

, Riemann hypothesis Poem about the Riemann hypothesis, sung by John Derbyshire
John Derbyshire
John Derbyshire is a British-American writer. His columns in National Review and cover a broad range of political-cultural topics, including immigration, China, history, mathematics, and race. Derbyshire's 1996 novel, Seeing Calvin Coolidge in a Dream, was a New York Times "Notable Book of the...

. (Slides for a lecture) (Reviews the GUE hypothesis, provides an extensive bibliography as well). including papers on the zeros of the zeta function and tables of the zeros of the zeta function Slides of a talk. A discussion of Xavier Gourdon's calculation of the first ten trillion non-trivial zeros., a simple animated Java applet.
Zetagrid (2002) A distributed computing project that attempted to disprove Riemann's hypothesis; closed in November 2005

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.