
Compass and straightedge
Encyclopedia


Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s, and other geometric figures using only an idealized
Idealization
Idealization is the process by which scientific models assume facts about the phenomenon being modeled that are strictly false. Often these assumptions are used to make models easier to understand or solve. Many times idealizations do not harm the predictive accuracy of the model for one reason or...
ruler
Ruler
A ruler, sometimes called a rule or line gauge, is an instrument used in geometry, technical drawing, printing and engineering/building to measure distances and/or to rule straight lines...
and compass
Compass (drafting)
A compass or pair of compasses is a technical drawing instrument that can be used for inscribing circles or arcs. As dividers, they can also be used as a tool to measure distances, in particular on maps...
.
The ruler to be used is assumed to be infinite in length, has no markings on it and only one edge, and is known as a straightedge
Straightedge
A straightedge is a tool with an edge free from curves, or straight, used for transcribing straight lines, or checking the straightness of lines...
. The compass is assumed to collapse when lifted from the page, so may not be directly used to transfer distances. (This is an unimportant restriction, as this may be achieved via the compass equivalence theorem
Compass equivalence theorem
The compass equivalence theorem is an important statement in compass and straightedge constructions. In these constructions it is assumed that whenever a compass is lifted from a page, it collapses, so that it may not be directly used to transfer distances...
.)
Every point constructible using straightedge and compass may be constructed using compass alone. A number of ancient problems in plane geometry impose this restriction.
The most famous ruler-and-compass problems have been proven impossible in several cases by Pierre Wantzel
Pierre Wantzel
Pierre Laurent Wantzel was a French mathematician who proved that several ancient geometric problems were impossible to solve using only compass and straightedge....
, using the mathematical theory of fields
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
. In spite of existing proofs of impossibility, some persist in trying to solve these problems. Many of these problems are easily solvable provided that other geometric transformations are allowed: for example, doubling the cube
Doubling the cube
Doubling the cube is one of the three most famous geometric problems unsolvable by compass and straightedge construction...
is possible using geometric constructions, but not possible using ruler and compass alone.
Mathematician Underwood Dudley
Underwood Dudley
Underwood Dudley is a mathematician, formerly of DePauw University, who has written a number of research works and textbooks but is best known for his popular writing. Most notable are several books describing crank mathematics by people who think they have squared the circle or done other...
has made a sideline of collecting false ruler-and-compass proofs, as well as other work by mathematical cranks
Crank (person)
"Crank" is a pejorative term used for a person who unshakably holds a belief that most of his or her contemporaries consider to be false. A "cranky" belief is so wildly at variance with commonly accepted belief as to be ludicrous...
, and has collected them into several books.
Compass and straightedge tools
The "compass" and "straightedge" of compass and straightedge constructions is an idealization of rulers and compasses in the real world:- The compass can be opened arbitrarily wide, but (unlike some real compassesCompass (drafting)A compass or pair of compasses is a technical drawing instrument that can be used for inscribing circles or arcs. As dividers, they can also be used as a tool to measure distances, in particular on maps...
) it has no markings on it. It can only be opened to widths that have already been constructed, and it collapses when not used for drawing. - The straightedge is infinitely long, but it has no markings on it and has only one edge, unlike ordinary rulers. It can only be used to draw a line segment between two points or to extend an existing line.
Each construction must be exact. "Eyeballing" it (essentially looking at the construction and guessing at its accuracy, or using some form of measurement, such as the units of measure on a ruler) and getting close does not count as a solution.
Stated this way, compass and straightedge constructions appear to be a parlour game
Parlour game
A parlour game is a group game played indoors. During the Victorian era in Great Britain and in the United States, these games were extremely popular among the upper and middle classes. They were often played in a parlour, hence the name....
, rather than a serious practical problem; but the purpose of the restriction is to ensure that constructions can be proven to be exactly correct, and is thus important to both drafting (design by both CAD software and traditional drafting with pencil, paper, straight-edge and compass) and the science of weights and measures, in which exact synthesis from reference bodies or materials is extremely important. One of the chief purposes of Greek mathematics was to find exact constructions for various lengths; for example, the side of a pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
inscribed in a given circle. The Greeks did not find constructions for three problems:
- Squaring the circleSquaring the circleSquaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
: Drawing a square the same area as a given circle. - Doubling the cubeDoubling the cubeDoubling the cube is one of the three most famous geometric problems unsolvable by compass and straightedge construction...
: Drawing a cube with twice the volume of a given cube. - Trisecting the angleAngle trisectionAngle trisection is a classic problem of compass and straightedge constructions of ancient Greek mathematics. It concerns construction of an angle equal to one-third of a given arbitrary angle, using only two tools: an un-marked straightedge, and a compass....
: Dividing a given angle into three smaller angles all of the same size.
For 2000 years people tried to find constructions within the limits set above, and failed. All three have now been proven under mathematical rules to be impossible generally (angles with certain values can be trisected, but not all possible angles.)
The basic constructions
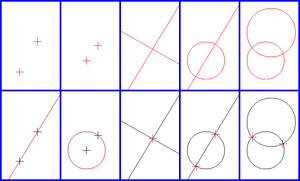
- Creating the line through two existing points
- Creating the circle through one point with centre another point
- Creating the point which is the intersection of two existing, non-parallel lines
- Creating the one or two points in the intersection of a line and a circle (if they intersect)
- Creating the one or two points in the intersection of two circles (if they intersect).
For example, starting with the minimal state of a drawing, with just two distinct points, we can create a line or either of two circles. From the two circles, two new points are created at their intersections. Drawing lines between the two original points and one of these new points completes the construction of an equilateral triangle.
Therefore, in any geometric problem we have an initial set of symbols (points and lines), an algorithm, and some results. From this perspective, geometry is equivalent to an axiomatic algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, replacing its elements by symbols. Probably Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
first realized this, and used it to prove the impossibility of some constructions; only much later did Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
find a complete set of axioms for geometry
Hilbert's axioms
Hilbert's axioms are a set of 20 assumptions proposed by David Hilbert in 1899 in his book Grundlagen der Geometrie , as the foundation for a modern treatment of Euclidean geometry...
.
Constructible points and lengths

Formal proof
There are many different ways to prove something is impossible. A more rigorous proof would be to demarcate the limit of the possible, and show that to solve these problems one must transgress that limit. Much of what can be constructed is covered in intercept theoryIntercept theorem
The intercept theorem, also known as Thales' theorem , is an important theorem in elementary geometry about the ratios of various line segments that are created if two intersecting lines are intercepted by a pair of parallels. It is equivalent to the theorem about ratios in similar triangles...
.
We could associate an algebra to our geometry using a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
made of two lines, and represent points of our plane by vector
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s. Finally we can write these vectors as complex numbers.
Using the equations for lines and circles, one can show that the points at which they intersect lie in a quadratic extension
Kummer theory
In abstract algebra and number theory, Kummer theory provides a description of certain types of field extensions involving the adjunction of nth roots of elements of the base field. The theory was originally developed by Ernst Eduard Kummer around the 1840s in his pioneering work on Fermat's last...
of the smallest field F containing two points on the line, the center of the circle, and the radius of the circle. That is, they are of the form
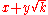 , where x, y, and k are in F.
, where x, y, and k are in F.Since the field of constructible points is closed under square roots, it contains all points that can be obtained by a finite sequence of quadratic extensions of the field of complex numbers with rational coefficients. By the above paragraph, one can show that any constructible point can be obtained by such a sequence of extensions. As a corollary of this, one finds that the degree of the minimal polynomial for a constructible point (and therefore of any constructible length) is a power of 2. In particular, any constructible point (or length) is an algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
, though not every algebraic number (for example 3√2) is constructible (i.e. the relationship between constructible lengths and algebraic numbers is not bijective).
Constructible angles
There is a bijectionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the angles that are constructible and the points that are constructible on any constructible circle. The angles that are constructible form an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under addition modulo 2π (which corresponds to multiplication of the points on the unit circle viewed as complex numbers). The angles that are constructible are exactly those whose tangent (or equivalently, sine or cosine) is constructible as a number. For example the regular heptadecagon
Heptadecagon
In geometry, a heptadecagon is a seventeen-sided polygon.-Heptadecagon construction:The regular heptadecagon is a constructible polygon, as was shown by Carl Friedrich Gauss in 1796 at the age of 19....
is constructible because

as discovered by Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
.
The group of constructible angles is closed under the operation that halves angles (which corresponds to taking square roots). The only angles of finite order that may be constructed starting with two points are those whose order is either a power of two, or a product of a power of two and a set of distinct Fermat primes. In addition there is a dense set of constructible angles of infinite order.
Compass and straightedge constructions as complex arithmetic
Given a set of points in the Euclidean plane, selecting any one of them to be called 0 and another to be called 1, together with an arbitrary choice of orientationOrientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
allows us to consider the points as a set of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
Given any such interpretation of a set of points as complex numbers, the points constructible using valid compass and straightedge constructions alone are precisely the elements of the smallest field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
containing the original set of points and closed under the complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
and square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
operations (to avoid ambiguity, we can specify the square root with complex argument less than π). The elements of this field are precisely those that may be expressed as a formula in the original points using only the operations of addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
, complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
, and square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
, which is easily seen to be a countable dense subset of the plane. Each of these six operations corresponding to a simple compass and straightedge construction. From such a formula it is straightforward to produce a construction of the corresponding point by combining the constructions for each of the arithmetic operations. More efficient constructions of a particular set of points correspond to shortcuts in such calculations.
Equivalently (and with no need to arbitrarily choose two points) we can say that, given an arbitrary choice of orientation, a set of points determines a set of complex ratios given by the ratios of the differences between any two pairs of points. The set of ratios constructible using compass and straightedge from such a set of ratios is precisely the smallest field containing the original ratios and closed under taking complex conjugates and square roots.
For example the real part, imaginary part and modulus of a point or ratio z (taking one of the two viewpoints above) are constructible as these may be expressed as
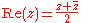
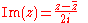
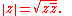
Doubling the cube and trisection of an angle (except for special angles such as any φ such that φ/6π is a rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
with denominator the product of a power of two and a set of distinct Fermat primes) require ratios which are the solution to cubic equations, while squaring the circle requires a transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
ratio. None of these are in the fields described, hence no compass and straightedge construction for these exists.
Squaring the circle
The most famous of these problems, squaring the circleSquaring the circle
Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
, otherwise known as the quadrature of the circle, involves constructing a square with the same area as a given circle using only straightedge and compass.
Squaring the circle has been proven impossible, as it involves generating a transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
ratio, that is,
 . Only certain algebraic
. Only certain algebraicAlgebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
ratios can be constructed with ruler and compass alone, namely those constructed from the integers with a finite sequence of operations of addition, subtraction, multiplication, division, and square roots. The phrase "squaring the circle" is often used to mean "doing the impossible" for this reason.
Without the constraint of requiring solution by ruler and compass alone, the problem is easily solvable by a wide variety of geometric and algebraic means, and has been solved many times in antiquity.
Doubling the cube
Doubling the cube: using only a straight-edge and compass, construct the side of a cube that has twice the volume of a cube with a given side. This is impossible because the cube root of 2, though algebraic, cannot be computed from integers by addition, subtraction, multiplication, division, and taking square roots. This follows because its minimal polynomial over the rationals has degree 3. This construction is possible using a ruler with two marks on it and a compass.Angle trisection
Angle trisection: using only a ruler and a compass, construct an angle that is one-third of a given arbitrary angle. This is impossible in the general case. For example: though the angle of π/3 radianRadian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s (60°
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
) cannot be trisected, the angle 2π/5 radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s (72° = 360º/5) can be trisected.
Constructing regular polygons
Some regular polygonRegular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s (e.g. a pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
) are easy to construct with ruler and compass; others are not. This led to the question: Is it possible to construct all regular polygons with ruler and compass?
Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in 1796 showed that a regular n-sided polygon can be constructed with ruler and compass if the odd prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s of n are distinct Fermat primes. Gauss conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
d that this condition was also necessary, but he offered no proof of this fact, which was provided by Pierre Wantzel
Pierre Wantzel
Pierre Laurent Wantzel was a French mathematician who proved that several ancient geometric problems were impossible to solve using only compass and straightedge....
in 1837.
Constructing with only ruler or only compass
It is possible (according to the Mohr–Mascheroni theoremMohr–Mascheroni theorem
In mathematics, the Mohr–Mascheroni theorem states that any geometric construction that can be performed by a compass and straightedge can be performed by a compass alone. The result was originally published by Georg Mohr in 1672, but his proof languished in obscurity until 1928. The theorem was...
) to construct anything with just a compass if it can be constructed with a ruler and compass, provided that the given data and the data to be found consist of discrete points (not lines or circles). It is impossible to take a square root with just a ruler, so some things that cannot be constructed with a ruler can be constructed with a compass; but (by the Poncelet–Steiner theorem) given a single circle and its center, they can be constructed.
Markable rulers
ArchimedesArchimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
and Apollonius
Apollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
gave constructions involving the use of a markable ruler. This would permit them, for example, to take a line segment, two lines (or circles), and a point; and then draw a line which passes through the given point and intersects both lines, and such that the distance between the points of intersection equals the given segment. This the Greeks called neusis
Neusiß
Neusiß is a municipality in the district Ilm-Kreis, in Thuringia, Germany....
("inclination", "tendency" or "verging"), because the new line tends to the point.
In this expanded scheme, any distance whose ratio to an existing distance is the solution of a cubic or a quartic equation is constructible. It follows that, if markable rulers and neusis are permitted, the trisection of the angle (see Archimedes' trisection) and the duplication of the cube can be achieved; the quadrature of the circle is still impossible. Some regular polygons, like the heptagon, become constructible; and John H. Conway gives constructions for several of them; but the 11-sided polygon, the hendecagon
Hendecagon
In geometry, a hendecagon is an 11-sided polygon....
, is still impossible, and infinitely many others.
When only an angle trisector is permitted, there is a complete description of all regular polygons which can be constructed, including above mentioned regular heptagon, triskaidecagon (13-gon) and enneadecagon
Enneadecagon
In geometry, an enneadecagon is a polygon with 19 sides and angles. It is also known as an enneakaidecagon or a nonadecagon.The radius of the circumcircle of the regular enneadecagon with side length t is...
(19-gon). It is open whether there are infinitely many primes p for which a regular p-gon is constructible with ruler, compass and an angle trisector.
Origami
The mathematical theory of origamiMathematics of paper folding
The art of origami or paper folding has received a considerable amount of mathematical study. Fields of interest include a given paper model's flat-foldability and the use of paper folds to solve mathematical equations.-Flat folding:The construction of origami models is sometimes shown as crease...
is more powerful than compass and staightedge construction. Folds satisfying the Huzita-Hatori axioms can construct exactly the same set of points as the extended constructions using a compass and a marked ruler. Therefore origami
Origami
is the traditional Japanese art of paper folding, which started in the 17th century AD at the latest and was popularized outside Japan in the mid-1900s. It has since then evolved into a modern art form...
can also be used to solve cubic equations (and hence quartic equations), and thus solve two of the classical problems .
The extension field
In abstract terms, using these more powerful tools of either neusis using a markable ruler or the constructions of origami extendsAlgebraic extension
In abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
the field of constructible number
Constructible number
A point in the Euclidean plane is a constructible point if, given a fixed coordinate system , the point can be constructed with unruled straightedge and compass...
s to a larger subfield of the complex numbers, which contains not only the square root, but also the cube roots, of every element. The arithmetic formulae for constructible points described above have analogies in this larger field, allowing formulae that include cube roots as well. The field extension generated by any additional point constructible in this larger field has degree a multiple of a power of two and a power of three, and may be broken into a tower of extensions of degree 2 and 3.
Recent research
Simon PlouffeSimon Plouffe
Simon Plouffe is a Quebec mathematician born on June 11, 1956 in Saint-Jovite, Quebec. He discovered the formula for the BBP algorithm which permits the computation of the nth binary digit of π, in 1995...
has written a paper showing how ruler and compass can be used as a simple computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
with unexpected power to compute binary digits of certain numbers.
See also
- Constructible numberConstructible numberA point in the Euclidean plane is a constructible point if, given a fixed coordinate system , the point can be constructed with unruled straightedge and compass...
- Constructible polygonConstructible polygonIn mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not....
- GeometrographyGeometrographyIn mathematics, in geometry, geometrography is the study of geometrical constructions. The concepts and methods of geometrography were first expounded by Émile Lemoine , a French civil engineer and a mathematician, in a meeting of the French Association for the Advancement of the Sciences held at...
- Interactive geometry softwareInteractive geometry softwareInteractive geometry software are computer programs which allow one to create and then manipulate geometric constructions, primarily in plane geometry. In most IGS, one starts construction by putting a few points and using them to define new objects such as lines, circles or other points...
may allow the user to create and manipulate ruler-and-compass constructions. - List of interactive geometry software, most of them show compass and straightedge constructions
- Mohr–Mascheroni theoremMohr–Mascheroni theoremIn mathematics, the Mohr–Mascheroni theorem states that any geometric construction that can be performed by a compass and straightedge can be performed by a compass alone. The result was originally published by Georg Mohr in 1672, but his proof languished in obscurity until 1928. The theorem was...
- Poncelet–Steiner theorem
External links
- Van Schooten's Ruler Constructions at Convergence
- Online ruler-and-compass construction tool
- Squaring the circle
- Impossibility of squaring the circle
- Doubling the cube
- Angle trisection
- An Investigation of Historical Geometric Constructions at Convergence
- Trisection of an Angle
- Regular polygon constructions
- Simon Plouffe's use of ruler and compass as a computer
- Why Gauss could not have proved necessity of constructible regular polygons
- Construction with the Compass Only at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Renaissance artists' constructions of regular polygons at Convergence
- Angle Trisection by Hippocrates
- Various constructions using compass and straightedge With interactive animated step-by-step instructions
- Math Tricks Help You Design Shop Projects: master a simple compass and you're a designer; convert your router into one with a trammel and away you go, Popular Science, May 1971, p104,106,108, Scanned article via Google Books: http://books.google.com/books?id=ngAAAAAAMBAJ&pg=PA104

