
Brachistochrone curve
Encyclopedia

A Brachistochrone curve (Gr. βραχίστος, brachistos - the shortest, χρόνος, chronos - time), or curve of fastest descent, is the curve between two points that is covered in the least time by a point-like body that starts at the first point with zero speed and is constrained to move along the curve to the second point, under the action of constant gravity and assuming no friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
.
The brachistochrone is the cycloid
Given two points A and B, with A not lower than B, there is just one upside down cycloidCycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
that passes through A with infinite slope, passes also through B and does not have maximum points between A and B. This particular inverted cycloid is a brachistochrone curve. The curve does not depend on the body's mass or on the strength of the gravitational constant.
The problem can be solved with the tools from the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
.
If the body is given an initial velocity at A, or if friction is taken into account, the curve that minimizes time will differ from the one described above.
Johann Bernoulli's solution
According to Fermat’s principle: The actual path between two points taken by a beam of light is the one which is traversed in the least time. Johann BernoulliJohann Bernoulli
Johann Bernoulli was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family...
used this principle to derive the brachistochrone curve by considering the trajectory of a beam of light in a medium where the speed of light increases following a constant vertical acceleration (that of gravity g).
The conservation law
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
can be used to express the speed of a body in a constant gravitational field as:
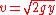 ,
,where y represents the vertical distance the body has fallen. By conservation of energy the speed of motion of the body along an arbitrary curve does not depend on the horizontal displacement.
Johann Bernoulli
Johann Bernoulli
Johann Bernoulli was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family...
noted that the law of refraction
Snell's law
In optics and physics, Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass...
gives a constant of the motion for a beam of light in a medium of variable density:
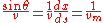 ,
,where vm is the constant and
 represents the angle of the trajectory with respect to the vertical.
represents the angle of the trajectory with respect to the vertical.The equations above allow us to draw two conclusions:
- At the onset, when the particle speed is nil, the angle must be nil. Hence, the brachistochrone curve is tangentTangentIn geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the vertical at the origin. - The speed reaches a maximum value when the trajectory becomes horizontal and the angle θ = 90°.
To keep things simple we can assume that the particle (or the beam) with coordinates (x,y) departs from the point (0,0) and reaches maximum speed after a falling a vertical distance D. So,
 .
.Rearranging terms in the law of refraction and squaring gives:

which can be solved for dx in terms of dy:
 .
.Substituting from the expressions for v and vm above gives:
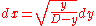
which is the differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
of an inverted cycloid
Cycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
generated by a circle of diameter D.
Johann's brother Jakob showed how 2nd differentials can be used to obtain the condition for least time. A modernized version of the proof is as follows. If we make a negligible deviation from the path of least time then, for the differential triangle formed by the displacement along the path and the horizontal and vertical displacements,
 .
.On differentiation with dy fixed we get,
 .
.And finally rearranging terms gives,

where the last part is just the change in distance for given change in time for 2nd differentials. Now consider the changes along the two neighboring paths in the figure below for which the horizontal separation between paths along the central line is d2x (the same for both the upper and lower differential triangles). Along the old and new paths, the parts that differ are,


For the path of least times these times are equal so for their difference we get,
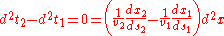
And the condition for least time is,

History
Johann Bernoulli posed the problem of the brachistochrone to the readers of Acta EruditorumActa Eruditorum
Acta Eruditorum was the first scientific journal of the German lands, published from 1682 to 1782....
in June, 1696. He published his solution in the journal in May of the following year, and noted that the solution is the same curve as Huygens's tautochrone curve
Tautochrone curve
A tautochrone or isochrone curve is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point...
. After deriving the differential equation for the curve by the method given above, he went on to show that it does yield a cycloid. But his proof is marred by the fact that he uses a single constant instead of the three constants, vm, 2g and D, above. Five mathematicians responded with solutions: Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
, Jakob Bernoulli (Johann's brother), Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
, Ehrenfried Walther von Tschirnhaus
Ehrenfried Walther von Tschirnhaus
Ehrenfried Walther von Tschirnhaus was a German mathematician, physicist, physician, and philosopher...
and Guillaume de l'Hôpital
Guillaume de l'Hôpital
Guillaume François Antoine, Marquis de l'Hôpital was a French mathematician. His name is firmly associated with l'Hôpital's rule for calculating limits involving indeterminate forms 0/0 and ∞/∞...
. Four of the solutions (excluding l'Hôpital's) were published in the same edition of the journal as Johann Bernoulli's. In his paper Jakob Bernoulli gave a proof of the condition for least time similar to that above before showing that its solution is a cycloid.
In an attempt to outdo his brother, Jakob Bernoulli created a harder version of the brachistochrone problem. In solving it, he developed new methods that were refined by Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
into what the latter called (in 1766) the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
. Joseph-Louis de Lagrange did further work that resulted in modern infinitesimal calculus
Infinitesimal calculus
Infinitesimal calculus is the part of mathematics concerned with finding slope of curves, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz and Isaac Newton starting in the 1660s...
.
Galileo tried to solve a similar problem for the path of the fastest descent from a point to a wall in his Two New Sciences
Two New Sciences
The Discourses and Mathematical Demonstrations Relating to Two New Sciences was Galileo's final book and a sort of scientific testament covering much of his work in physics over the preceding thirty years.After his Dialogue Concerning the Two Chief World Systems, the Roman Inquisition had banned...
in 1638. He draws the conclusion (Third Day, Theorem 22, Prop. 36) that the arc of a circle is faster than any number of its chords,
- "From the preceding it is possible to infer that the quickest path of all [lationem omnium velocissimam], from one point to another, is not the shortest path, namely, a straight line, but the arc of a circle.
- ...
- Consequently the nearer the inscribed polygon approaches a circle the shorter is the time required for descent from A to C. What has been proven for the quadrant holds true also for smaller arcs; the reasoning is the same."
We are warned earlier in the Discourses (just after Theorem 6) of possible fallacies and the need for a "higher science." In this dialogue Galileo reviews his own work. The actual solution to Galileo's problem is half a cycloid. Galileo studied the cycloid and gave it its name, but the connection between it and his problem had to wait for advances in mathematics.
See also
- Calculus of variationsCalculus of variationsCalculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
- Beltrami identityBeltrami identityThe Beltrami identity is an identity in the calculus of variations. It says that a function u which is an extremal of the integralI=\int_a^b L \, dxsatisfies the differential equation...
- CycloidCycloidA cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
- Tautochrone curveTautochrone curveA tautochrone or isochrone curve is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point...
- CatenaryCatenaryIn physics and geometry, the catenary is the curve that an idealised hanging chain or cable assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola...
- uniformly accelerated motion
External links
- http://www.mathcurve.com/courbes2d/brachistochrone/brachistochrone.shtml (in FrenchFrench languageFrench is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
but has an excellent animated illustration) - The Brachistochrone, Whistler Alley Mathematics.
- Table IV from Bernoulli's article in Acta Eruditorum 1697
- Brachistochrones by Michael Trott and Brachistochrone Problem by Okay Arik, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. - The Brachistochrone problem at MacTutor

