
Butterfly effect
Encyclopedia

Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
, the butterfly effect is the sensitive dependence on initial conditions; where a small change at one place in a nonlinear system can result in large differences to a later state. The name of the effect, coined by Edward Lorenz, is derived from the theoretical example of a hurricane's formation being contingent on whether or not a distant butterfly had flapped its wings several weeks before.
Although the butterfly effect may appear to be an esoteric and unusual behavior, it is exhibited by very simple systems: for example, a ball
Ball
A ball is a round, usually spherical but sometimes ovoid, object with various uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used for simpler activities, such as catch, marbles and juggling...
placed at the crest of a hill might roll into any of several valleys depending on slight differences in initial position.
The butterfly effect is a common trope
Trope (literature)
A literary trope is the usage of figurative language in literature, or a figure of speech in which words are used in a sense different from their literal meaning...
in fiction when presenting scenarios involving time travel
Time travel
Time travel is the concept of moving between different points in time in a manner analogous to moving between different points in space. Time travel could hypothetically involve moving backward in time to a moment earlier than the starting point, or forward to the future of that point without the...
and with "what if" cases where one storyline diverges at the moment of a seemingly minor event resulting in two significantly different outcomes.
Theory
RecurrencePoincaré recurrence theorem
In mathematics, the Poincaré recurrence theorem states that certain systems will, after a sufficiently long time, return to a state very close to the initial state. The Poincaré recurrence time is the length of time elapsed until the recurrence. The result applies to physical systems in which...
, the approximate return of a system towards its initial conditions, together with sensitive dependence on initial conditions, are the two main ingredients for chaotic motion. They have the practical consequence of making complex system
Complex system
A complex system is a system composed of interconnected parts that as a whole exhibit one or more properties not obvious from the properties of the individual parts....
s, such as the weather
Weather
Weather is the state of the atmosphere, to the degree that it is hot or cold, wet or dry, calm or stormy, clear or cloudy. Most weather phenomena occur in the troposphere, just below the stratosphere. Weather refers, generally, to day-to-day temperature and precipitation activity, whereas climate...
, difficult to predict past a certain time range (approximately a week in the case of weather), since it is impossible to measure the starting atmospheric conditions completely accurately.
Origin of the concept and the term
The term "butterfly effect" itself is related to the work of Edward Lorenz, and it is based in chaos theoryChaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
and sensitive dependence on initial conditions, already described in the literature in a particular case of the three-body problem
Three-body problem
Three-body problem has two distinguishable meanings in physics and classical mechanics:# In its traditional sense the three-body problem is the problem of taking an initial set of data that specifies the positions, masses and velocities of three bodies for some particular point in time and then...
by Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
in 1890. He later proposed that such phenomena could be common, say in meteorology.
In 1898, Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
noted general divergence of trajectories in spaces of negative curvature, and Pierre Duhem
Pierre Duhem
Pierre Maurice Marie Duhem was a French physicist, mathematician and philosopher of science, best known for his writings on the indeterminacy of experimental criteria and on scientific development in the Middle Ages...
discussed the possible general significance of this in 1908. The idea that one butterfly
Butterfly
A butterfly is a mainly day-flying insect of the order Lepidoptera, which includes the butterflies and moths. Like other holometabolous insects, the butterfly's life cycle consists of four parts: egg, larva, pupa and adult. Most species are diurnal. Butterflies have large, often brightly coloured...
could eventually have a far-reaching ripple effect
Ripple effect
The ripple effect is a term used to describe a situation where, like the ever expanding ripples across water when an object is dropped into it, an effect from an initial state can be followed outwards incrementally....
on subsequent historic events first appears in "A Sound of Thunder
A Sound of Thunder
“A Sound of Thunder” is a science fiction short story by Ray Bradbury, first published in Collier’s magazine in 1952. As of 1984 it was the most re-published science fiction story up to the present time...
", a 1952 short story by Ray Bradbury
Ray Bradbury
Ray Douglas Bradbury is an American fantasy, horror, science fiction, and mystery writer. Best known for his dystopian novel Fahrenheit 451 and for the science fiction stories gathered together as The Martian Chronicles and The Illustrated Man , Bradbury is one of the most celebrated among 20th...
about time travel (see Literature and print here) although Lorenz made the term popular.
In 1961, Lorenz was using a numerical computer model to rerun a weather prediction, when, as a shortcut on a number in the sequence, he entered the decimal .506 instead of entering the full .506127. The result was a completely different weather scenario. Lorenz published his findings in a 1963 paper for the New York Academy of Sciences
New York Academy of Sciences
The New York Academy of Sciences is the third oldest scientific society in the United States. An independent, non-profit organization with more than members in 140 countries, the Academy’s mission is to advance understanding of science and technology...
noting that "One meteorologist remarked that if the theory were correct, one flap of a seagull
Gull
Gulls are birds in the family Laridae. They are most closely related to the terns and only distantly related to auks, skimmers, and more distantly to the waders...
's wings could change the course of weather forever." Following suggestions from colleagues, in later speeches and papers Lorenz used the more poetic butterfly
Butterfly
A butterfly is a mainly day-flying insect of the order Lepidoptera, which includes the butterflies and moths. Like other holometabolous insects, the butterfly's life cycle consists of four parts: egg, larva, pupa and adult. Most species are diurnal. Butterflies have large, often brightly coloured...
. According to Lorenz, when Lorenz failed to provide a title for a talk he was to present at the 139th meeting of the American Association for the Advancement of Science
American Association for the Advancement of Science
The American Association for the Advancement of Science is an international non-profit organization with the stated goals of promoting cooperation among scientists, defending scientific freedom, encouraging scientific responsibility, and supporting scientific education and science outreach for the...
in 1972, Philip Merilees concocted Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas? as a title. Although a butterfly flapping its wings has remained constant in the expression of this concept, the location of the butterfly, the consequences, and the location of the consequences have varied widely.
The phrase refers to the idea that a butterfly's wings might create tiny changes in the atmosphere
Earth's atmosphere
The atmosphere of Earth is a layer of gases surrounding the planet Earth that is retained by Earth's gravity. The atmosphere protects life on Earth by absorbing ultraviolet solar radiation, warming the surface through heat retention , and reducing temperature extremes between day and night...
that may ultimately alter the path of a tornado
Tornado
A tornado is a violent, dangerous, rotating column of air that is in contact with both the surface of the earth and a cumulonimbus cloud or, in rare cases, the base of a cumulus cloud. They are often referred to as a twister or a cyclone, although the word cyclone is used in meteorology in a wider...
or delay, accelerate or even prevent the occurrence of a tornado in another location. The flapping wing represents a small change in the initial condition of the system, which causes a chain of events leading to large-scale alterations of events (compare: domino effect
Domino effect
The domino effect is a chain reaction that occurs when a small change causes a similar change nearby, which then will cause another similar change, and so on in linear sequence. The term is best known as a mechanical effect, and is used as an analogy to a falling row of dominoes...
). Had the butterfly not flapped its wings, the trajectory of the system might have been vastly different. While the butterfly does not "cause" the tornado in the sense of providing the energy for the tornado, it does "cause" it in the sense that the flap of its wings is an essential part of the initial conditions resulting in a tornado, and without that flap that particular tornado would not have existed.
Illustration
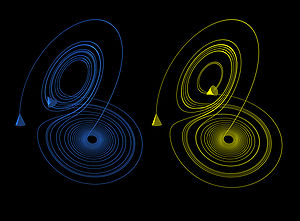
| The butterfly effect in the Lorenz attractor Lorenz attractor The Lorenz attractor, named for Edward N. Lorenz, is an example of a non-linear dynamic system corresponding to the long-term behavior of the Lorenz oscillator. The Lorenz oscillator is a 3-dimensional dynamical system that exhibits chaotic flow, noted for its lemniscate shape... |
||
|---|---|---|
| time 0 ≤ t ≤ 30 (larger) | z coordinate (larger) | |
 |
 |
|
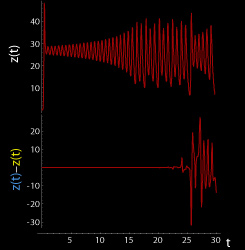
| These figures show two segments of the three-dimensional evolution of two trajectories (one in blue, the other in yellow) for the same period of time in the Lorenz attractor Lorenz attractor The Lorenz attractor, named for Edward N. Lorenz, is an example of a non-linear dynamic system corresponding to the long-term behavior of the Lorenz oscillator. The Lorenz oscillator is a 3-dimensional dynamical system that exhibits chaotic flow, noted for its lemniscate shape... starting at two initial points that differ only by 10−5 in the x-coordinate. Initially, the two trajectories seem coincident, as indicated by the small difference between the z coordinate of the blue and yellow trajectories, but for t > 23 the difference is as large as the value of the trajectory. The final position of the cones indicates that the two trajectories are no longer coincident at t = 30. |
||
| A Java animation of the Lorenz attractor shows the continuous evolution. | ||
Mathematical definition
A dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
displays sensitive dependence on initial conditions if points arbitrarily close together separate over time at an exponential rate. The definition is not topological, but essentially metrical.
If M is the state space for the map
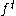 , then
, then  displays sensitive dependence to initial conditions if for any x in M and any δ > 0, there are y in M, with
displays sensitive dependence to initial conditions if for any x in M and any δ > 0, there are y in M, with 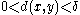 such that
such that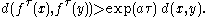
The definition does not require that all points from a neighborhood separate from the base point x, but it requires one positive Lyapunov exponent
Lyapunov exponent
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories...
.
Examples
The butterfly effect is most familiar in terms of weather; it can easily be demonstrated in standard weather prediction models, for example.The potential for sensitive dependence on initial conditions (the butterfly effect) has been studied in a number of cases in semiclassical and quantum physics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
including atoms in strong fields and the anisotropic Kepler problem
Kepler problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive...
. Some authors have argued that extreme (exponential) dependence on initial conditions is not expected in pure quantum treatments; however, the sensitive dependence on initial conditions demonstrated in classical motion is included in the semiclassical treatments developed by Martin Gutzwiller
Martin Gutzwiller
Martin C. Gutzwiller is a physicist. He is known for the invention of the variational wave-function describing electrons with strong localized interactions , for the first investigation of relations between classical and quantum mechanics in chaotic systems , as well as new solutions to...
and Delos and co-workers.
Other authors suggest that the butterfly effect can be observed in quantum systems. Karkuszewski et al. consider the time evolution of quantum systems which have slightly different Hamiltonians. They investigate the level of sensitivity of quantum systems to small changes in their given Hamiltonians. Poulin et al. present a quantum algorithm to measure fidelity decay, which “measures the rate at which identical initial states diverge when subjected to slightly different dynamics.” They consider fidelity decay to be “the closest quantum analog to the (purely classical) butterfly effect.” Whereas the classical butterfly effect considers the effect of a small change in the position and/or velocity of an object in a given Hamiltonian system
Hamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
, the quantum butterfly effect considers the effect of a small change in the Hamiltonian system
Hamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
with a given initial position and velocity. This quantum butterfly effect has been demonstrated experimentally. Quantum and semiclassical treatments of system sensitivity to initial conditions are known as quantum chaos
Quantum chaos
Quantum chaos is a branch of physics which studies how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is, "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle...
.
See also
- Avalanche effectAvalanche effectIn cryptography, the avalanche effect refers to a desirable property of cryptographic algorithms, typically block ciphers and cryptographic hash functions. The avalanche effect is evident if, when an input is changed slightly the output changes significantly...
- Behavioral cuspBehavioral cuspA behavioral cusp is any behavior change that brings an organism's behavior into contact with new contingencies that have far-reaching consequences...
- Cascading failureCascading failureA cascading failure is a failure in a system of interconnected parts in which the failure of a part can trigger the failure of successive parts.- Cascading failure in power transmission :...
- CausalityCausalityCausality is the relationship between an event and a second event , where the second event is understood as a consequence of the first....
- Chain reactionChain reactionA chain reaction is a sequence of reactions where a reactive product or by-product causes additional reactions to take place. In a chain reaction, positive feedback leads to a self-amplifying chain of events....
- DeterminismDeterminismDeterminism is the general philosophical thesis that states that for everything that happens there are conditions such that, given them, nothing else could happen. There are many versions of this thesis. Each of them rests upon various alleged connections, and interdependencies of things and...
- Domino effectDomino effectThe domino effect is a chain reaction that occurs when a small change causes a similar change nearby, which then will cause another similar change, and so on in linear sequence. The term is best known as a mechanical effect, and is used as an analogy to a falling row of dominoes...
- Dynamical systems
- FractalFractalA fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
- Innovation butterflyInnovation butterflyThe Innovation Butterfly is a metaphor that describes how seemingly minor perturbations to project plans in a system connecting markets, demand, product features, and a firm's capabilities can steer the project, or an entire portfolio of projects, down an irreversible path in terms of technology...
- Kessler syndromeKessler syndromeThe Kessler syndrome , proposed by NASA scientist Donald J...
- Law of unintended consequences
- Positive feedbackPositive feedbackPositive feedback is a process in which the effects of a small disturbance on a system include an increase in the magnitude of the perturbation. That is, A produces more of B which in turn produces more of A. In contrast, a system that responds to a perturbation in a way that reduces its effect is...
- Snowball effectSnowball effectSnowball effect is a figurative term for a process that starts from an initial state of small significance and builds upon itself, becoming larger , and perhaps potentially dangerous or disastrous , though it might be beneficial instead...
- Traffic congestionTraffic congestionTraffic congestion is a condition on road networks that occurs as use increases, and is characterized by slower speeds, longer trip times, and increased vehicular queueing. The most common example is the physical use of roads by vehicles. When traffic demand is great enough that the interaction...
- Tropical cyclogenesisTropical cyclogenesisTropical cyclogenesis is the term that describes the development and strengthening of a tropical cyclone in the atmosphere. The mechanisms through which tropical cyclogenesis occurs are distinctly different from those through which mid-latitude cyclogenesis occurs...
External links
- The meaning of the butterfly: Why pop culture loves the 'butterfly effect,' and gets it totally wrong, Peter Dizikes, Boston Globe, June 8, 2008
- From butterfly wings to single e-mail (Cornell UniversityCornell UniversityCornell University is an Ivy League university located in Ithaca, New York, United States. It is a private land-grant university, receiving annual funding from the State of New York for certain educational missions...
) - New England Complex Systems Institute - Concepts: Butterfly Effect
- The Chaos Hypertextbook. An introductory primer on chaos and fractals
- ChaosBook.org. Advanced graduate textbook on chaos (no fractals)

