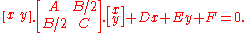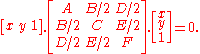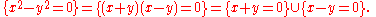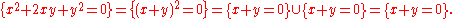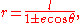
Conic section
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a conic section (or just conic) is a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
obtained by intersecting a cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
(more precisely, a right circular conical surface
Conical surface
In geometry, a conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the apex or vertex — and any point of some fixed space curve — the directrix — that does not contain the apex...
) with a plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
. In analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, a conic may be defined as a plane algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
of degree 2. It can be defined as the locus
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of points whose distances are in a fixed ratio to some point, called a focus
Focus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
, and some line, called a directrix.
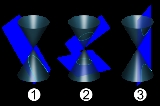
The three types of conic section are the hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
, the parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, and the ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
. The circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
is a special case of the ellipse, and is of sufficient interest in its own right that it is sometimes called the fourth type of conic section.
The conic sections were named and studied as long ago as 200 BC, when Apollonius of Perga
Apollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
undertook a systematic study of their properties.
Menaechmus
It is believed that the first definition of a conic section is due to MenaechmusMenaechmus
Menaechmus was an ancient Greek mathematician and geometer born in Alopeconnesus in the Thracian Chersonese, who was known for his friendship with the renowned philosopher Plato and for his apparent discovery of conic sections and his solution to the then-long-standing problem of doubling the cube...
. This work does not survive, however, and is only known through secondary accounts. The definition used at that time differs from the one commonly used today in that it requires the plane cutting the cone to be perpendicular to one of the lines that generate the cone as a surface of revolution (a generatrix). Thus the shape of the conic is determined by the angle formed at the vertex of the cone (between two opposite generatrices): If the angle is acute then the conic is an ellipse; if the angle is right then the conic is a parabola; and if the angle is obtuse then the conic is a hyperbola. Note that the circle cannot be defined this way and was not considered a conic at this time.
Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
is said to have written four books on conics but these were lost as well. Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
is known to have studied conics, having determined the area bounded by a parabola and an ellipse. The only part of this work to survive is a book on the solids of revolution of conics.
Apollonius of Perga
The greatest progress in the study of conics by the ancient Greeks is due to Apollonius of PergaApollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
, whose eight volume Conic Sections summarized the existing knowledge at the time and greatly extended it. Apollonius's major innovation was to characterize a conic using properties within the plane and intrinsic to the curve; this greatly simplified analysis. With this tool, it was now possible to show that any plane cutting the cone, regardless of its angle, will produce a conic according to the earlier definition, leading to the definition commonly used today.
Pappus
Pappus of Alexandria
Pappus of Alexandria was one of the last great Greek mathematicians of Antiquity, known for his Synagoge or Collection , and for Pappus's Theorem in projective geometry...
is credited with discovering importance of the concept of a focus of a conic, and the discovery of the related concept of a directrix.
Al-Kuhi
An instrument for drawing conic sections was first described in 1000 CE by the Islamic mathematician Al-Kuhi.Omar Khayyám
Apollonius's work was translated into Arabic (the technical language of the time) and much of his work only survives through the Arabic version. Persians found applications to the theory; the most notable of these was the Persian mathematician and poet Omar KhayyámOmar Khayyám
Omar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....
who used conic sections to solve algebraic equations.
Europe
Johannes KeplerJohannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
extended the theory of conics through the "principle of continuity", a precursor to the concept of limits. Girard Desargues and Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
developed a theory of conics using an early form of projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
and this helped to provide impetus for the study of this new field. In particular, Pascal discovered a theorem known as the hexagrammum mysticum from which many other properties of conics can be deduced. Meanwhile, René Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
applied his newly discovered Analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
to the study of conics. This had the effect of reducing the geometrical problems of conics to problems in algebra.
Features

Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, and hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
. The circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
can be considered as a fourth type (as it was by Apollonius) or as a kind of ellipse. The circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
and the ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
arise when the intersection of cone and plane is a closed curve. The circle is obtained when the cutting plane is parallel to the plane of the generating circle of the cone – for a right cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
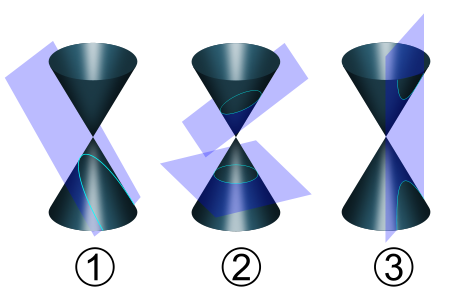
as in the picture at the top of the page this means that the cutting plane is perpendicular to the symmetry axis of the cone. If the cutting plane is parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
to exactly one generating line of the cone, then the conic is unbounded and is called a parabola. In the remaining case, the figure is a hyperbola. In this case, the plane will intersect both halves (nappes) of the cone, producing two separate unbounded curves.
Various parameters are associated with a conic section, as shown in the following table. (For the ellipse, the table gives the case of a>b, for which the major axis is horizontal; for the reverse case, interchange the symbols a and b. For the hyperbola the east-west opening case is given. In all cases, a and b are positive.)
| conic section | equation | eccentricity (e) | linear eccentricity (c) | semi-latus rectum (ℓ) | focal parameter (p) |
|---|---|---|---|---|---|
| circle Circle A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius.... |
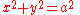 |
 |
 |
 |
 |
| ellipse Ellipse In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis... |
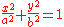 |
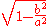 |
 |
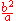 |
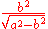 |
| parabola Parabola In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface... |
 |
 |
 |
 |
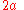 |
| hyperbola Hyperbola In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror... |
 |
 |
 |
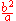 |
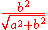 |
Conic sections are exactly those curves that, for a point F, a line L not containing F and a non-negative number e, are the locus
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of points whose distance to F equals e times their distance to L. F is called the focus
Focus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
, L the directrix, and e the eccentricity
Eccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
.
The linear eccentricity (c) is the distance between the center and the focus (or one of the two foci).
The latus rectum (2ℓ) is the chord
Chord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
parallel to the directrix and passing through the focus (or one of the two foci).
The semi-latus rectum (ℓ) is half the latus rectum.
The focal parameter (p) is the distance from the focus (or one of the two foci) to the directrix.
The following relations hold:
Properties
Just as two (distinct) points determine a line, five points determine a conicFive points determine a conic
In geometry, just as two points determine a line , five points determine a conic . There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines.Formally, given any five points in the plane in general...
. Formally, given any five points in the plane in general linear position, meaning no three collinear
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, there is a unique conic passing through them, which will be non-degenerate; this is true over both the affine plane and projective plane. Indeed, given any five points there is a conic passing through them, but if three of the points are collinear the conic will be degenerate (reducible, because it contains a line), and may not be unique; see further discussion.
Irreducible conic sections are always "smooth". More precisely, they never contain any inflection point
Inflection point
In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
s. This is important for many applications, such as aerodynamics, where a smooth surface is required to ensure laminar flow
Laminar flow
Laminar flow, sometimes known as streamline flow, occurs when a fluid flows in parallel layers, with no disruption between the layers. At low velocities the fluid tends to flow without lateral mixing, and adjacent layers slide past one another like playing cards. There are no cross currents...
and to prevent turbulence
Turbulence
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
.
Intersection at infinity
An algebro-geometricallyAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
intrinsic form of this classification is by the intersection of the conic with the line at infinity
Line at infinity
In geometry and topology, the line at infinity is a line that is added to the real plane in order to give closure to, and remove the exceptional cases from, the incidence properties of the resulting projective plane. The line at infinity is also called the ideal line.-Geometric formulation:In...
, which gives further insight into their geometry:
- ellipses intersect the line at infinity in 0 points – rather, in 0 real points, but in 2 complex points, which are conjugateComplex conjugateIn mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
; - parabolas intersect the line at infinity in 1 double point, corresponding to the axis – they are tangent to the line at infinity, and close at infinity, as distended ellipses;
- hyperbolas intersect the line at infinity in 2 points, corresponding to the asymptotes – hyperbolas pass through infinity, with a twist. Going to infinity along one branch passes through the point at infinity corresponding to the asymptote, then re-emerges on the other branch at the other side but with the inside of the hyperbola (the direction of curvature) on the other side – left vs. right (corresponding to the non-orientability of the real projective planeReal projective planeIn mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
) – and then passing through the other point at infinity returns to the first branch. Hyperbolas can thus be seen as ellipses that have been pulled through infinity and re-emerged on the other side, flipped.
Degenerate cases
There are five degenerate cases: three in which the plane passes through apex of the cone, and three that arise when the cone itself degenerates to a cylinder (a doubled line can occur in both cases).When the plane passes through the apex, the resulting conic is always degenerate, and is either: a point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
(when the angle between the plane and the axis of the cone is larger than tangential); a straight line (when the plane is tangential to the surface of the cone); or a pair of intersecting lines (when the angle is smaller than the tangential). These correspond respectively to degeneration of an ellipse, parabola, and a hyperbola, which are characterized in the same way by angle. The straight line is more precisely a double line (a line with multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
2) because the plane is tangent to the cone, and thus the intersection should be counted twice.
Where the cone is a cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
, i.e. with the vertex at infinity, cylindric sections are obtained; this corresponds to the apex being at infinity. Cylindrical sections are ellipses (or circles), unless the plane is vertical (which corresponds to passing through the apex at infinity), in which case three degenerate cases occur: two parallel lines, known as a ribbon (corresponding to an ellipse with one axis infinite and the other axis real and non-zero, the distance between the lines), a double line (an ellipse with one infinite axis and one axis zero), and no intersection (an ellipse with one infinite axis and the other axis imaginary).
Eccentricity, focus and directrix
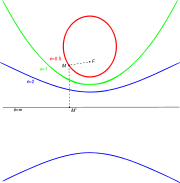
 (the focus), a line
(the focus), a line 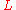 (the directrix) not containing
(the directrix) not containing  and a nonnegative real number
and a nonnegative real number  (the eccentricity
(the eccentricityEccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
). The corresponding conic section consists of the locus
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of all points whose distance to
 equals
equals  times their distance to
times their distance to 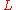 . For
. For 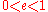 we obtain an ellipse, for
we obtain an ellipse, for  a parabola, and for
a parabola, and for  a hyperbola.
a hyperbola.For an ellipse and a hyperbola, two focus-directrix combinations can be taken, each giving the same full ellipse or hyperbola. The distance from the center to the directrix is
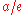 , where
, where  is the semi-major axis
is the semi-major axisSemi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
of the ellipse, or the distance from the center to the tops of the hyperbola. The distance from the center to a focus is
 .
.In the case of a circle, the eccentricity
 , and one can imagine the directrix to be infinitely far removed from the center. However, the statement that the circle consists of all points whose distance to F is e times the distance to L is not useful, because we get zero times infinity.
, and one can imagine the directrix to be infinitely far removed from the center. However, the statement that the circle consists of all points whose distance to F is e times the distance to L is not useful, because we get zero times infinity.The eccentricity of a conic section is thus a measure of how far it deviates from being circular.
For a given
 , the closer
, the closer  is to 1, the smaller is the semi-minor axis
is to 1, the smaller is the semi-minor axisSemi-minor axis
In geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...
.
Generalizations
Conics may be defined over other fields, and may also be classified in the projective plane rather than in the affine plane.Over the complex numbers ellipses and hyperbolas are not distinct, since there is no meaningful difference between 1 and −1; precisely, the ellipse
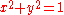 becomes a hyperbola under the substitution
becomes a hyperbola under the substitution  geometrically a complex rotation, yielding
geometrically a complex rotation, yielding 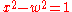 – a hyperbola is simply an ellipse with an imaginary axis length. Thus there is a 2-way classification: ellipse/hyperbola and parabola. Geometrically, this corresponds to intersecting the line at infinity in either 2 distinct points (corresponding to two asymptotes) or in 1 double point (corresponding to the axis of a parabola), and thus the real hyperbola is a more suggestive image for the complex ellipse/hyperbola, as it also has 2 (real) intersections with the line at infinity.
– a hyperbola is simply an ellipse with an imaginary axis length. Thus there is a 2-way classification: ellipse/hyperbola and parabola. Geometrically, this corresponds to intersecting the line at infinity in either 2 distinct points (corresponding to two asymptotes) or in 1 double point (corresponding to the axis of a parabola), and thus the real hyperbola is a more suggestive image for the complex ellipse/hyperbola, as it also has 2 (real) intersections with the line at infinity.In projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, over any division ring, but in particular over either the real or complex numbers, all non-degenerate conics are equivalent, and thus in projective geometry one simply speaks of "a conic" without specifying a type, as type is not meaningful. Geometrically, the line at infinity
Line at infinity
In geometry and topology, the line at infinity is a line that is added to the real plane in order to give closure to, and remove the exceptional cases from, the incidence properties of the resulting projective plane. The line at infinity is also called the ideal line.-Geometric formulation:In...
is no longer special (distinguished), so while some conics intersect the line at infinity differently, this can be changed by a projective transformation – pulling an ellipse out to infinity or pushing a parabola off infinity to an ellipse or a hyperbola.
In other areas of mathematics
The classification into elliptic, parabolic, and hyperbolic is pervasive in mathematics, and often divides a field into sharply distinct subfields. The classification mostly arises due to the presence of a quadratic form (in two variables this corresponds to the associated discriminantDiscriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
), but can also correspond to eccentricity.
Quadratic form classifications:
quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s: Quadratic forms over the reals are classified by Sylvester's law of inertia
Sylvester's law of inertia
Sylvester's law of inertia is a theorem in matrix algebra about certain properties of the coefficient matrix of a real quadratic form that remain invariant under a change of coordinates...
, namely by their positive index, zero index, and negative index: a quadratic form in n variables can be converted to a diagonal form, as
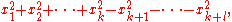 where the number of +1 coefficients, k, is the positive index, the number of −1 coefficients, l, is the negative index, and the remaining variables are the zero index m, so
where the number of +1 coefficients, k, is the positive index, the number of −1 coefficients, l, is the negative index, and the remaining variables are the zero index m, so 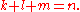 In two variables the non-zero quadratic forms are classified as:
In two variables the non-zero quadratic forms are classified as:
-
 – positive-definite (the negative is also included), corresponding to ellipses,
– positive-definite (the negative is also included), corresponding to ellipses, -
 – degenerate, corresponding to parabolas, and
– degenerate, corresponding to parabolas, and -
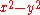 – indefinite, corresponding to hyperbolas.
– indefinite, corresponding to hyperbolas.
- In two variables quadratic forms are classified by discriminant, analogously to conics, but in higher dimensions the more useful classification is as definite, (all positive or all negative), degenerate, (some zeros), or indefinite (mix of positive and negative but no zeros). This classification underlies many that follow.
curvature: The Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
of a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
describes the infinitesimal geometry, and may at each point be either positive – elliptic geometry
Elliptic geometry
Elliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
, zero – Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
(flat, parabola), or negative – hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
; infinitesimally, to second order the surface looks like the graph of
 ,
, 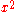 (or 0), or
(or 0), or 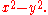 . Indeed, by the uniformization theorem
. Indeed, by the uniformization theoremUniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
every surface can be taken to be globally (at every point) positively curved, flat, or negatively curved. In higher dimensions the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
is a more complicated object, but manifolds with constant sectional curvature are interesting objects of study, and have strikingly different properties, as discussed at sectional curvature
Sectional curvature
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
.
Second order PDEs: Partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s (PDEs) of second order are classified at each point as elliptic, parabolic, or hyperbolic, accordingly as their second order terms correspond to an elliptic, parabolic, or hyperbolic quadratic form. The behavior and theory of these different types of PDEs are strikingly different – representative examples is that the Laplacian is elliptic, the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
is parabolic, and the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
is hyperbolic.
Eccentricity classifications include:
Möbius transformations: Real Möbius transformations (elements of PSL2(R) or its 2-fold cover, SL2(R)) are classified as elliptic, parabolic, or hyperbolic accordingly as their half-trace is
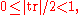
 or
or 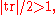 mirroring the classification by eccentricity.
mirroring the classification by eccentricity.Variance-to-mean ratio: The variance-to-mean ratio classifies several important families of discrete probability distributions: the constant distribution as circular (eccentricity 0), binomial distributions as elliptical, Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
s as parabolic, and negative binomial distribution
Negative binomial distribution
In probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
s as hyperbolic. This is elaborated at cumulants of some discrete probability distributions.
Cartesian coordinates
In the Cartesian coordinate systemCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, the graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of a quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
in two variables is always a conic section – though it may be degenerate, and all conic sections arise in this way. The equation will be of the form
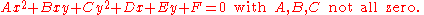
As scaling all six constants yields the same locus of zeros, one can consider conics as points in the five-dimensional projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....

Discriminant classification
The conic sections described by this equation can be classified with the discriminantDiscriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
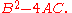
If the conic is non-degenerate, then:
- if
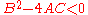 , the equation represents an ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, the equation represents an ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
;- if
 and
and  , the equation represents a circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, the equation represents a circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, which is a special case of an ellipse;
- if
- if
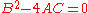 , the equation represents a parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, the equation represents a parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
; - if
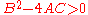 , the equation represents a hyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
, the equation represents a hyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
;- if we also have
 , the equation represents a rectangular hyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
, the equation represents a rectangular hyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
.
- if we also have
To distinguish the degenerate cases from the non-degenerate cases, let ∆ be the determinant of the 3×3 matrix [A, B/2, D/2 ; B/2, C, E/2 ; D/2, E/2, F ]: that is, ∆ = (AC - B2/4)F + BED/4 - CD2/4 - AE2/4. Then the conic section is non-degenerate if and only if ∆ ≠ 0. If ∆=0 we have a point ellipse, two parallel lines (possibly coinciding with each other) in the case of a parabola, or two intersecting lines in the case of a hyperbola.
Moreover, in the case of a non-degenerate ellipse (with
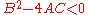 and ∆≠0), we have a real ellipse if C∆ < 0 but an imaginary ellipse if C∆ > 0. An example is
and ∆≠0), we have a real ellipse if C∆ < 0 but an imaginary ellipse if C∆ > 0. An example is  , which has no real-valued solutions.
, which has no real-valued solutions.Note that A and B are polynomial coefficients, not the lengths of semi-major/minor axis as defined in some sources.
Matrix notation
The above equation can be written in matrix notation asThe type of conic section is solely determined by the determinant of middle matrix: if it is positive, zero, or negative then the conic is an ellipse, parabola, or hyperbola respectively (see geometric meaning of a quadratic form). If both the eigenvalues of the middle matrix are non-zero (i.e. it is an ellipse or a hyperbola), we can do a transformation of variables to obtain
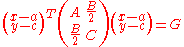
where a,c, and G satisfy
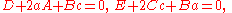 and
and  .
.The quadratic can also be written as
If the determinant of this 3×3 matrix is non-zero, the conic section is not degenerate. If the determinant equals zero, the conic is a degenerate parabola (two parallel or coinciding lines), a degenerate ellipse (a point ellipse), or a degenerate hyperbola (two intersecting lines).
Note that in the centered equation with constant term G, G equals minus one times the ratio of the 3×3 determinant to the 2×2 determinant.
As slice of quadratic form
The equation
can be rearranged by taking the affine linear part to the other side, yielding

In this form, a conic section is realized exactly as the intersection of the graph of the quadratic form
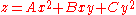 and the plane
and the plane  Parabolas and hyperbolas can be realized by a horizontal plane (
Parabolas and hyperbolas can be realized by a horizontal plane (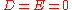 ), while ellipses require that the plane be slanted. Degenerate conics correspond to degenerate intersections, such as taking slices such as
), while ellipses require that the plane be slanted. Degenerate conics correspond to degenerate intersections, such as taking slices such as 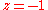 of a positive-definite form.
of a positive-definite form.Eccentricity in terms of parameters of the quadratic form
When the conic section is written algebraically as
the eccentricity can be written as a function of the parameters of the quadratic equation. If 4AC = B2 the conic is a parabola and its eccentricity equals 1 (if it is non-degenerate). Otherwise, assuming the equation represents either a non-degenerate hyperbola or a non-degenerate, non-imaginary ellipse, the eccentricity is given by

where
 = 1 if the determinant of the 3×3 matrix is negative or
= 1 if the determinant of the 3×3 matrix is negative or  = -1 if that determinant is positive.
= -1 if that determinant is positive.Standard form
Through change of coordinates these equations can be put in standard forms:- Circle:

- Ellipse:

- Parabola:
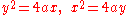
- Hyperbola:
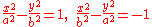
- Rectangular Hyperbola:

Such forms will be symmetrical about the x-axis and for the circle, ellipse and hyperbola symmetrical about the y-axis.
The rectangular hyperbola however is only symmetrical about the lines
 and
and 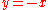 . Therefore its inverse function is exactly the same as its original function.
. Therefore its inverse function is exactly the same as its original function.These standard forms can be written as parametric equation
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
s,
- CircleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
: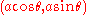 ,
, - EllipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
: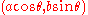 ,
, - ParabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
: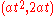 ,
, - HyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
: or
or 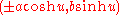 .
. - Rectangular hyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
: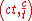
Invariants of conics
The traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
and determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of
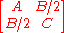 are both invariant with respect to both rotation of axes
are both invariant with respect to both rotation of axesRotation of Axes
A rotation of axes is a form of Euclidean transformation in which the entire xy-coordinate system is rotated in the counter-clockwise direction with respect to the origin through a scalar quantity denoted by θ....
and translation of the plane (movement of the origin).
The constant term F is invariant under rotation only.
Modified form
.For some practical applications, it is important to re-arrange the standard form so that the focal-point can be placed at the origin. The mathematical formulation for a general conic section is then given in the polar form by

and in the Cartesian form by
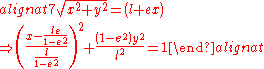
From the above equation, the linear eccentricity (c) is given by
 .
.From the general equations given above, different conic sections can be represented as shown below:
- Circle:
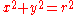
- Ellipse:
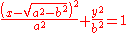
- Parabola:

- Hyperbola:
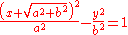
Homogeneous coordinates
In homogeneous coordinatesHomogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
a conic section can be represented as:
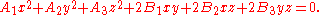
Or in matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
notation
The matrix
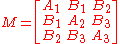 is called the matrix of the conic section.
is called the matrix of the conic section. is called the determinant
is called the determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the conic section. If Δ = 0 then the conic section is said to be degenerate; this means that the conic section is either a union of two straight lines, a repeated line, a point or the empty set.
For example, the conic section
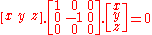 reduces to the union of two lines:
reduces to the union of two lines:Similarly, a conic section sometimes reduces to a (single) repeated line:
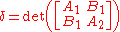 is called the discriminant
is called the discriminantDiscriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
of the conic section. If δ = 0 then the conic section is a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, if δ < 0, it is an hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
and if δ > 0, it is an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
. A conic section is a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
if δ > 0 and A1 = A2 and B1 = 0, it is an rectangular hyperbola if δ < 0 and A1 = −A2. It can be proven that in the complex projective plane CP2 two conic sections have four points in common (if one accounts for multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
), so there are never more than 4 intersection
Line-line intersection
In Euclidean geometry, the intersection of a line and a line can be the empty set,a point, ora line. Distinguishing these cases, and finding the intersection point have use, for example, in computer graphics, motion planning, and collision detection....
points and there is always one intersection point (possibilities: four distinct intersection points, two singular intersection points and one double intersection points, two double intersection points, one singular intersection point and 1 with multiplicity 3, 1 intersection point with multiplicity 4). If there exists at least one intersection point with multiplicity > 1, then the two conic sections are said to be tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
. If there is only one intersection point, which has multiplicity 4, the two conic sections are said to be osculating.
Furthermore each straight line intersects each conic section twice. If the intersection point is double, the line is said to be tangent and it is called the tangent line.
Because every straight line intersects a conic section twice, each conic section has two points at infinity
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
(the intersection points with the line at infinity
Line at infinity
In geometry and topology, the line at infinity is a line that is added to the real plane in order to give closure to, and remove the exceptional cases from, the incidence properties of the resulting projective plane. The line at infinity is also called the ideal line.-Geometric formulation:In...
). If these points are real, the conic section must be a hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
, if they are imaginary conjugated, the conic section must be an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, if the conic section has one double point at infinity it is a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. If the points at infinity are (1,i,0) and (1,-i,0), the conic section is a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
. If a conic section has one real and one imaginary point at infinity or it has two imaginary points that are not conjugated it is neither a parabola nor an ellipse nor a hyperbola.
Polar coordinates
In polar coordinatesPolar coordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
, a conic section with one focus at the origin and, if any, the other on the x-axis, is given by the equation
where e is the eccentricity and l is the semi-latus rectum (see below).
As above, for e = 0, we have a circle, for 0 < e < 1 we obtain an ellipse, for e = 1 a parabola, and for e > 1 a hyperbola.

Applications
Conic sections are important in astronomyAstronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
: the orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
s of two massive objects that interact according to Newton's law of universal gravitation are conic sections if their common center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
is considered to be at rest. If they are bound together, they will both trace out ellipses; if they are moving apart, they will both follow parabolas or hyperbolas. See two-body problem.
In projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, the conic sections in the projective plane are equivalent to each other up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
projective transformations.
For specific applications of each type of conic section, see the articles circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, and hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
.
For certain fossil
Fossil
Fossils are the preserved remains or traces of animals , plants, and other organisms from the remote past...
s in paleontology
Paleontology
Paleontology "old, ancient", ὄν, ὀντ- "being, creature", and λόγος "speech, thought") is the study of prehistoric life. It includes the study of fossils to determine organisms' evolution and interactions with each other and their environments...
, understanding conic sections can help understand the three-dimensional shape of certain organisms.
Intersecting two conics
The solutions to a two second degree equations system in two variables may be seen as the coordinates of the intersections of two generic conic sections.In particular two conics may possess none, two or four possibly coincident intersection points.
The best method of locating these solutions exploits the homogeneous matrix representation of conic sections, i.e. a 3x3 symmetric matrix which depends on six parameters.
The procedure to locate the intersection points follows these steps:
- given the two conics
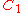 and
and 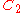 consider the pencil of conics given by their linear combination
consider the pencil of conics given by their linear combination 
- identify the homogeneous parameters
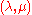 which corresponds to the degenerate conic of the pencil. This can be done by imposing that
which corresponds to the degenerate conic of the pencil. This can be done by imposing that  , which turns out to be the solution to a third degree equation.
, which turns out to be the solution to a third degree equation. - given the degenerate conic
 , identify the two, possibly coincident, lines constituting it
, identify the two, possibly coincident, lines constituting it - intersects each identified line with one of the two original conic; this step can be done efficiently using the dual conic representation of

- the points of intersection will represent the solution to the initial equation system
See also
- Focus (geometry)Focus (geometry)In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
, an overview of properties of conic sections related to the foci - Lambert conformal conic projectionLambert conformal conic projectionA Lambert conformal conic projection is a conic map projection, which is often used for aeronautical charts. In essence, the projection superimposes a cone over the sphere of the Earth, with two reference parallels secant to the globe and intersecting it. This minimizes distortion from projecting...
- Matrix representation of conic sections
- QuadricQuadricIn mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
s, the higher-dimensional analogs of conics - Quadratic functionQuadratic functionA quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
- Rotation of axesRotation of AxesA rotation of axes is a form of Euclidean transformation in which the entire xy-coordinate system is rotated in the counter-clockwise direction with respect to the origin through a scalar quantity denoted by θ....
- Dandelin spheresDandelin spheresIn geometry, the Dandelin spheres are one or two spheres that are tangent both to a plane and to a cone that intersects the plane. The intersection of the cone and the plane is a conic section, and the point at which either sphere touches the plane is a focus of the conic section, so the Dandelin...
- Projective conics
- Elliptic coordinatesElliptic coordinatesIn geometry, the elliptic coordinate system is a two-dimensional orthogonal coordinate system in whichthe coordinate lines are confocal ellipses and hyperbolae...
- Parabolic coordinatesParabolic coordinatesParabolic coordinates are a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal parabolas. A three-dimensional version of parabolic coordinates is obtained by rotating the two-dimensional system about the symmetry axis of the parabolas.Parabolic coordinates have...
- Director circleDirector circleIn geometry, the director circle of an ellipse or hyperbola is a circle formed by the points where two perpendicular tangent lines to the curve cross....
External links
- Derivations of Conic Sections at Convergence
- Conic sections at Special plane curves.
- Determinants and Conic Section Curves
- Occurrence of the conics. Conics in nature and elsewhere.
- Conics. An essay on conics and how they are generated.
- See Conic Sections at cut-the-knot for a sharp proof that any finite conic section is an ellipse and Xah Lee for a similar treatment of other conics.
- Cone-plane intersection MATLABMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
code - Eight Point Conic at Dynamic Geometry Sketches
- An interactive Java conics grapher; uses a general second-order implicit equation.