
Galois theory
Encyclopedia
In mathematics
, more specifically in abstract algebra
, Galois theory, named after Évariste Galois
, provides a connection between field theory
and group theory
. Using Galois theory, certain problems in field theory can be reduced to group theory, which is in some sense simpler and better understood.
Originally Galois used permutation group
s to describe how the various roots of a given polynomial
equation are related to each other. The modern approach to Galois theory, developed by Richard Dedekind
, Leopold Kronecker and Emil Artin
, among others, involves studying automorphism
s of field extension
s.
Further abstraction of Galois theory is achieved by the theory of Galois connection
s.
.
Galois theory not only provides a beautiful answer to this question, it also explains in detail why it is possible to solve equations of degree four or lower in the above manner, and why their solutions take the form that they do. Further, it gives a conceptually clear, and often practical, means of telling when some particular equation of higher degree can be solved in that manner.
Galois theory also gives a clear insight into questions concerning problems in compass and straightedge
construction.
It gives an elegant characterisation of the ratios of lengths that can be constructed with this method.
Using this, it becomes relatively easy to answer such classical problems of geometry as
s in the roots. For instance, , where 1, and ab are the elementary polynomials of degree 0, 1 and 2 in two variables.
This was first formalized by the 16th century French mathematician François Viète
, in Viète's formulas, for the case of positive real roots. In the opinion of the 18th century British mathematician Charles Hutton
, the expression of coefficients of a polynomial in terms of the roots (not only for positive roots) was first understood by the 17th century French mathematician Albert Girard
; Hutton writes:
In this vein, the discriminant
is a symmetric function in the roots which reflects properties of the roots – it is zero if and only if the polynomial has a multiple root, and for quadratic and cubic polynomials it is positive if and only if all roots are real and distinct, and negative if and only if there is a pair of distinct complex conjugate roots. See Discriminant: nature of the roots for details.
The cubic was first partly solved by the 15th/16th century Italian mathematician Scipione del Ferro
, who did not however publish his results; this method only solved one of three classes, as the others involved taking square roots of negative numbers, and complex numbers were not known at the time. This solution was then rediscovered independently in 1535 by Niccolò Fontana Tartaglia
, who shared it with Gerolamo Cardano
, asking him to not publish it. Cardano then extended this to the other two cases, using square roots of negatives as intermediate steps; see details at Cardano's method. After the discovery of Ferro's work, he felt that Tartaglia's method was no longer secret, and thus he published his complete solution in his 1545 Ars Magna
. His student Lodovico Ferrari
solved the quartic polynomial, which solution Cardano also included in Ars Magna.
A further step was the 1770 paper Réflexions sur la résolution algébrique des équations by the French-Italian mathematician Joseph Louis Lagrange
, in his method of Lagrange resolvents, where he analyzed Cardano and Ferrarri's solution of cubics and quartics by considering them in terms of permutations of the roots, which yielded an auxiliary polynomial of lower degree, providing a unified understanding of the solutions and laying the groundwork for group theory and Galois theory. Crucially, however, he did not consider composition of permutations. Lagrange's method did not extend to quintic equations or higher, because the resolvent had higher degree.
The quintic was almost proven to have no general solutions by radicals by Paolo Ruffini
in 1799, whose key insight was to use permutation groups
, not just a single permutation. His solution contained a gap, which Cauchy considered minor, though this was not patched until the work of Norwegian mathematician Niels Henrik Abel
, who published a proof in 1824, thus establishing the Abel–Ruffini theorem
.
While Ruffini and Abel established that the general quintic could not be solved, some particular quintics can be solved, such as (x − 1)5=0, and the precise criterion by which a given quintic or higher polynomial could be determined to be solvable or not was given by Évariste Galois
, who showed that whether a polynomial was solvable or not was equivalent to whether or not the permutation group of its roots – in modern terms, its Galois group
– had a certain structure – in modern terms, whether or not it was a solvable group
. This group was always solvable for polynomials of degree four or less, but not always so for polynomials of degree five and greater, which explains why there is no general solution in higher degree.
s (or rearrangements) of the roots having the property that any algebraic equation satisfied by the roots is still satisfied after the roots have been permuted. An important proviso is that we restrict ourselves to algebraic equations whose coefficients are rational number
s. (One might instead specify a certain field
in which the coefficients should lie but, for the simple examples below, we will restrict ourselves to the field of rational numbers.)
These permutations together form a permutation group
, also called the Galois group
of the polynomial (over the rational numbers). To illustrate this point, consider the following examples:

By using the quadratic formula, we find that the two roots are
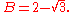
Examples of algebraic equations satisfied by A and B include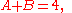
and

Obviously, in either of these equations, if we exchange A and B, we obtain another true statement. For example, the equation A + B = 4 becomes simply B + A = 4. Furthermore, it is true, but far less obvious, that this holds for every possible algebraic equation with rational coefficients satisfied by the roots A and B; to prove this requires the theory of symmetric polynomial
s.
We conclude that the Galois group of the polynomial x2 − 4x + 1 consists of two permutations: the identity permutation which leaves A and B untouched, and the transposition permutation which exchanges A and B. It is a cyclic group
of order two, and therefore isomorphic
to Z/2Z.
One might object that A and B are related by yet another algebraic equation,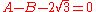
which does not remain true when A and B are exchanged. However, this equation does not concern us, because it does not have rational coefficients; in particular,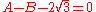 is not rational.
is not rational.
A similar discussion applies to any quadratic polynomial ax2 + bx + c, where a, b and c are rational numbers.
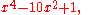
which can also be written as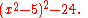
We wish to describe the Galois group of this polynomial, again over the field of rational number
s. The polynomial has four roots:



There are 24 possible ways to permute these four roots, but not all of these permutations are members of the Galois group. The members of the Galois group must preserve any algebraic equation with rational coefficients involving A, B, C and D. One such equation is
However, since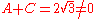 ,
,
the permutation → (A, B, D, C)
is not permitted (because it transforms the valid equation A + D = 0 into the invalid equation A + C = 0).
Another equation that the roots satisfy is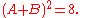
This will exclude further permutations, such as → (A, C, B, D).
Continuing in this way, we find that the only permutations (satisfying both equations simultaneously) remaining are → (A, B, C, D) → (C, D, A, B) → (B, A, D, C) → (D, C, B, A),
and the Galois group is isomorphic to the Klein four-group
.
L/K (read: L over K), and examines the group of field automorphisms of L/K (these are mappings α: L → L with α(x) = x for all x in K). See the article on Galois group
s for further explanation and examples.
The connection between the two approaches is as follows. The coefficients of the polynomial in question should be chosen from the base field K. The top field L should be the field obtained by adjoining the roots of the polynomial in question to the base field. Any permutation of the roots which respects algebraic equations as described above gives rise to an automorphism of L/K, and vice versa.
In the first example above, we were studying the extension Q(√3)/Q, where Q is the field of rational numbers, and Q(√3) is the field obtained from Q by adjoining √3. In the second example, we were studying the extension Q(A,B,C,D)/Q.
There are several advantages to the modern approach over the permutation group approach.
in group theory
allows one to determine whether a polynomial is solvable in radicals, depending on whether its Galois group has the property of solvability. In essence, each field extension L/K corresponds to a factor group in a composition series
of the Galois group. If a factor group in the composition series is cyclic
of order n, and if in the corresponding field extension L/K the field K already contains a primitive n-th root of unity
, then it is a radical extension and the elements of L can then be expressed using the nth root of some element of K.
If all the factor groups in its composition series are cyclic, the Galois group is called solvable, and all of the elements of the corresponding field can be found by repeatedly taking roots, products, and sums of elements from the base field (usually Q).
One of the great triumphs of Galois Theory was the proof that for every n > 4, there exist polynomials of degree n which are not solvable by radicals—the Abel–Ruffini theorem
. This is due to the fact that for n > 4 the symmetric group
Sn contains a simple
, non-cyclic, normal subgroup
, namely An.
cites the polynomial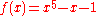 . By the rational root theorem this has no rational zeros. Neither does it have linear factors modulo 2 or 3.
. By the rational root theorem this has no rational zeros. Neither does it have linear factors modulo 2 or 3.
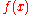 has the factorization
has the factorization 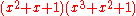 modulo 2. That means its Galois group modulo 2 is cyclic of order 6.
modulo 2. That means its Galois group modulo 2 is cyclic of order 6.
 has no linear or quadratic factor modulo 3, and hence is irreducible modulo 3. Thus its Galois group modulo 3 contains an element of order 5.
has no linear or quadratic factor modulo 3, and hence is irreducible modulo 3. Thus its Galois group modulo 3 contains an element of order 5.
It is known that a Galois group modulo a prime is isomorphic to a subgroup of the Galois group over the rationals. A permutation group on 5 objects with elements of orders 6 and 5 must be the symmetric group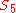 , which is therefore the Galois group of
, which is therefore the Galois group of  . This is one of the simplest examples of a non-solvable quintic polynomial. Serge Lang
. This is one of the simplest examples of a non-solvable quintic polynomial. Serge Lang
has said that Emil Artin
found this example.
.
For that, choose a field K and a finite group G. Cayley's theorem
says that G is (up to isomorphism) a subgroup of the symmetric group
S on the elements of G. Choose indeterminates {xα}, one for each element α of G, and adjoin them to K to get the field F = K({xα}). Contained within F is the field L of symmetric rational function
s in the {xα}. The Galois group of F/L is S, by a basic result of Emil Artin. G acts on F by restriction of action of S. If the fixed field of this action is M, then, by the fundamental theorem of Galois theory
, the Galois group of F/M is G.
It is an open problem to prove the existence of a field extension of the rational field Q with a given finite group as Galois group. Hilbert played a part in solving the problem for all symmetric and alternating groups. Igor Shafarevich
proved that every solvable finite group is the Galois group of some extension of Q. Various people have solved the inverse Galois problem for selected non-abelian simple group
s. Existence of solutions has been shown for all but possibly one (Mathieu group
M23) of the 26 sporadic simple groups. There is even a polynomial with integral coefficients whose Galois group is the Monster group
.
Online textbooks in French, German, Italian and English can be found at:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, Galois theory, named after Évariste Galois
Évariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
, provides a connection between field theory
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
and group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
. Using Galois theory, certain problems in field theory can be reduced to group theory, which is in some sense simpler and better understood.
Originally Galois used permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
s to describe how the various roots of a given polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equation are related to each other. The modern approach to Galois theory, developed by Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
, Leopold Kronecker and Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
, among others, involves studying automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s of field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
s.
Further abstraction of Galois theory is achieved by the theory of Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
s.
Application to classical problems
The birth of Galois theory was originally motivated by the following question, whose answer is known as the Abel–Ruffini theoremAbel–Ruffini theorem
In algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...
.
- Why is there no formula for the roots of a fifth (or higher) degree polynomial equation in terms of the coefficients of the polynomial, using only the usual algebraic operations (addition, subtraction, multiplication, division) and application of radicals (square roots, cube roots, etc)?
Galois theory not only provides a beautiful answer to this question, it also explains in detail why it is possible to solve equations of degree four or lower in the above manner, and why their solutions take the form that they do. Further, it gives a conceptually clear, and often practical, means of telling when some particular equation of higher degree can be solved in that manner.
Galois theory also gives a clear insight into questions concerning problems in compass and straightedge
Compass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
construction.
It gives an elegant characterisation of the ratios of lengths that can be constructed with this method.
Using this, it becomes relatively easy to answer such classical problems of geometry as
- Which regular polygonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s are constructible polygonConstructible polygonIn mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not....
s? - Why is it not possible to trisect every angle using a compass and straightedgeCompass and straightedgeCompass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
?
History
Galois theory originated in the study of symmetric functions – the coefficients of a monic polynomial are (up to sign) the elementary symmetric polynomialElementary symmetric polynomial
In mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
s in the roots. For instance, , where 1, and ab are the elementary polynomials of degree 0, 1 and 2 in two variables.
This was first formalized by the 16th century French mathematician François Viète
François Viète
François Viète , Seigneur de la Bigotière, was a French mathematician whose work on new algebra was an important step towards modern algebra, due to its innovative use of letters as parameters in equations...
, in Viète's formulas, for the case of positive real roots. In the opinion of the 18th century British mathematician Charles Hutton
Charles Hutton
Charles Hutton was an English mathematician.Hutton was born at Newcastle-on-Tyne. He was educated in a school at Jesmond, kept by Mr Ivison, a clergyman of the Church of England...
, the expression of coefficients of a polynomial in terms of the roots (not only for positive roots) was first understood by the 17th century French mathematician Albert Girard
Albert Girard
Albert Girard was a French-born mathematician. He studied at the University of Leiden. He "had early thoughts on the fundamental theorem of algebra" and gave the inductive definition for the Fibonacci numbers....
; Hutton writes:
...[Girard was] the first person who understood the general doctrine of the formation of the coefficients of the powers from the sum of the roots and their products. He was the first who discovered the rules for summing the powers of the roots of any equation.
In this vein, the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
is a symmetric function in the roots which reflects properties of the roots – it is zero if and only if the polynomial has a multiple root, and for quadratic and cubic polynomials it is positive if and only if all roots are real and distinct, and negative if and only if there is a pair of distinct complex conjugate roots. See Discriminant: nature of the roots for details.
The cubic was first partly solved by the 15th/16th century Italian mathematician Scipione del Ferro
Scipione del Ferro
Scipione del Ferro was an Italian mathematician who first discovered a method to solve the depressed cubic equation.-Life:Scipione del Ferro was born in Bologna, in northern Italy, to Floriano and Filippa Ferro...
, who did not however publish his results; this method only solved one of three classes, as the others involved taking square roots of negative numbers, and complex numbers were not known at the time. This solution was then rediscovered independently in 1535 by Niccolò Fontana Tartaglia
Niccolò Fontana Tartaglia
Niccolò Fontana Tartaglia was a mathematician, an engineer , a surveyor and a bookkeeper from the then-Republic of Venice...
, who shared it with Gerolamo Cardano
Gerolamo Cardano
Gerolamo Cardano was an Italian Renaissance mathematician, physician, astrologer and gambler...
, asking him to not publish it. Cardano then extended this to the other two cases, using square roots of negatives as intermediate steps; see details at Cardano's method. After the discovery of Ferro's work, he felt that Tartaglia's method was no longer secret, and thus he published his complete solution in his 1545 Ars Magna
Ars Magna (Gerolamo Cardano)
The Ars Magna is an important book on Algebra written by Gerolamo Cardano. It was first published in 1545 under the title Artis Magnæ, Sive de Regulis Algebraicis Liber Unus . There was a second edition in Cardano's lifetime, published in 1570...
. His student Lodovico Ferrari
Lodovico Ferrari
Lodovico Ferrari was an Italian mathematician.Born in Milan, Italy, grandfather, Bartholomew Ferrari was forced out of Milan to Bologna. He settled in Bologna, Italy and he began his career as the servant of Gerolamo Cardano. He was extremely bright, so Cardano started teaching him mathematics...
solved the quartic polynomial, which solution Cardano also included in Ars Magna.
A further step was the 1770 paper Réflexions sur la résolution algébrique des équations by the French-Italian mathematician Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
, in his method of Lagrange resolvents, where he analyzed Cardano and Ferrarri's solution of cubics and quartics by considering them in terms of permutations of the roots, which yielded an auxiliary polynomial of lower degree, providing a unified understanding of the solutions and laying the groundwork for group theory and Galois theory. Crucially, however, he did not consider composition of permutations. Lagrange's method did not extend to quintic equations or higher, because the resolvent had higher degree.
The quintic was almost proven to have no general solutions by radicals by Paolo Ruffini
Paolo Ruffini
Paolo Ruffini was an Italian mathematician and philosopher.By 1788 he had earned university degrees in philosophy, medicine/surgery, and mathematics...
in 1799, whose key insight was to use permutation groups
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
, not just a single permutation. His solution contained a gap, which Cauchy considered minor, though this was not patched until the work of Norwegian mathematician Niels Henrik Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
, who published a proof in 1824, thus establishing the Abel–Ruffini theorem
Abel–Ruffini theorem
In algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...
.
While Ruffini and Abel established that the general quintic could not be solved, some particular quintics can be solved, such as (x − 1)5=0, and the precise criterion by which a given quintic or higher polynomial could be determined to be solvable or not was given by Évariste Galois
Évariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
, who showed that whether a polynomial was solvable or not was equivalent to whether or not the permutation group of its roots – in modern terms, its Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
– had a certain structure – in modern terms, whether or not it was a solvable group
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
. This group was always solvable for polynomials of degree four or less, but not always so for polynomials of degree five and greater, which explains why there is no general solution in higher degree.
The permutation group approach to Galois theory
Given a polynomial, it may be that some of the roots are connected by various algebraic equations. For example, it may be that for two of the roots, say A and B, that . The central idea of Galois theory is to consider those permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s (or rearrangements) of the roots having the property that any algebraic equation satisfied by the roots is still satisfied after the roots have been permuted. An important proviso is that we restrict ourselves to algebraic equations whose coefficients are rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s. (One might instead specify a certain field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
in which the coefficients should lie but, for the simple examples below, we will restrict ourselves to the field of rational numbers.)
These permutations together form a permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
, also called the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of the polynomial (over the rational numbers). To illustrate this point, consider the following examples:
First example — a quadratic equation
Consider the quadratic equationQuadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...

By using the quadratic formula, we find that the two roots are

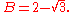
Examples of algebraic equations satisfied by A and B include
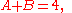
and

Obviously, in either of these equations, if we exchange A and B, we obtain another true statement. For example, the equation A + B = 4 becomes simply B + A = 4. Furthermore, it is true, but far less obvious, that this holds for every possible algebraic equation with rational coefficients satisfied by the roots A and B; to prove this requires the theory of symmetric polynomial
Symmetric polynomial
In mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
s.
We conclude that the Galois group of the polynomial x2 − 4x + 1 consists of two permutations: the identity permutation which leaves A and B untouched, and the transposition permutation which exchanges A and B. It is a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order two, and therefore isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to Z/2Z.
One might object that A and B are related by yet another algebraic equation,
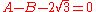
which does not remain true when A and B are exchanged. However, this equation does not concern us, because it does not have rational coefficients; in particular,
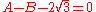 is not rational.
is not rational.A similar discussion applies to any quadratic polynomial ax2 + bx + c, where a, b and c are rational numbers.
- If the polynomial has only one root, for example x2 − 4x + 4 = (x−2)2, then the Galois group is trivial; that is, it contains only the identity permutation.
- If it has two distinct rational roots, for example x2 − 3x + 2 = (x−2)(x−1), the Galois group is again trivial.
- If it has two irrational roots (including the case where the roots are complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
), then the Galois group contains two permutations, just as in the above example.
Second example
Consider the polynomial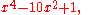
which can also be written as
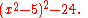
We wish to describe the Galois group of this polynomial, again over the field of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s. The polynomial has four roots:




There are 24 possible ways to permute these four roots, but not all of these permutations are members of the Galois group. The members of the Galois group must preserve any algebraic equation with rational coefficients involving A, B, C and D. One such equation is
- A + D = 0.
However, since
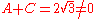 ,
,the permutation → (A, B, D, C)
is not permitted (because it transforms the valid equation A + D = 0 into the invalid equation A + C = 0).
Another equation that the roots satisfy is
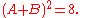
This will exclude further permutations, such as → (A, C, B, D).
Continuing in this way, we find that the only permutations (satisfying both equations simultaneously) remaining are → (A, B, C, D) → (C, D, A, B) → (B, A, D, C) → (D, C, B, A),
and the Galois group is isomorphic to the Klein four-group
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
.
The modern approach by field theory
In the modern approach, one starts with a field extensionField extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
L/K (read: L over K), and examines the group of field automorphisms of L/K (these are mappings α: L → L with α(x) = x for all x in K). See the article on Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
s for further explanation and examples.
The connection between the two approaches is as follows. The coefficients of the polynomial in question should be chosen from the base field K. The top field L should be the field obtained by adjoining the roots of the polynomial in question to the base field. Any permutation of the roots which respects algebraic equations as described above gives rise to an automorphism of L/K, and vice versa.
In the first example above, we were studying the extension Q(√3)/Q, where Q is the field of rational numbers, and Q(√3) is the field obtained from Q by adjoining √3. In the second example, we were studying the extension Q(A,B,C,D)/Q.
There are several advantages to the modern approach over the permutation group approach.
- It permits a far simpler statement of the fundamental theorem of Galois theoryFundamental theorem of Galois theoryIn mathematics, the fundamental theorem of Galois theory is a result that describes the structure of certain types of field extensions.In its most basic form, the theorem asserts that given a field extension E /F which is finite and Galois, there is a one-to-one correspondence between its...
. - The use of base fields other than Q is crucial in many areas of mathematics. For example, in algebraic number theoryAlgebraic number theoryAlgebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, one often does Galois theory using number fields, finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s or local fieldLocal fieldIn mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
s as the base field. - It allows one to more easily study infinite extensions. Again this is important in algebraic number theory, where for example one often discusses the absolute Galois groupAbsolute Galois groupIn mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
of Q, defined to be the Galois group of K/Q where K is an algebraic closureAlgebraic closureIn mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of Q. - It allows for consideration of inseparableSeparable extensionIn modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
extensions. This issue does not arise in the classical framework, since it was always implicitly assumed that arithmetic took place in characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero, but nonzero characteristic arises frequently in number theory and in algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. - It removes the rather artificial reliance on chasing roots of polynomials. That is, different polynomials may yield the same extension fields, and the modern approach recognizes the connection between these polynomials.
Solvable groups and solution by radicals
The notion of a solvable groupSolvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
allows one to determine whether a polynomial is solvable in radicals, depending on whether its Galois group has the property of solvability. In essence, each field extension L/K corresponds to a factor group in a composition series
Composition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
of the Galois group. If a factor group in the composition series is cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order n, and if in the corresponding field extension L/K the field K already contains a primitive n-th root of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
, then it is a radical extension and the elements of L can then be expressed using the nth root of some element of K.
If all the factor groups in its composition series are cyclic, the Galois group is called solvable, and all of the elements of the corresponding field can be found by repeatedly taking roots, products, and sums of elements from the base field (usually Q).
One of the great triumphs of Galois Theory was the proof that for every n > 4, there exist polynomials of degree n which are not solvable by radicals—the Abel–Ruffini theorem
Abel–Ruffini theorem
In algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...
. This is due to the fact that for n > 4 the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn contains a simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
, non-cyclic, normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
, namely An.
A non-solvable quintic example
Van der WaerdenBartel Leendert van der Waerden
Bartel Leendert van der Waerden was a Dutch mathematician and historian of mathematics....
cites the polynomial
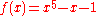 . By the rational root theorem this has no rational zeros. Neither does it have linear factors modulo 2 or 3.
. By the rational root theorem this has no rational zeros. Neither does it have linear factors modulo 2 or 3.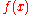 has the factorization
has the factorization 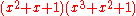 modulo 2. That means its Galois group modulo 2 is cyclic of order 6.
modulo 2. That means its Galois group modulo 2 is cyclic of order 6. has no linear or quadratic factor modulo 3, and hence is irreducible modulo 3. Thus its Galois group modulo 3 contains an element of order 5.
has no linear or quadratic factor modulo 3, and hence is irreducible modulo 3. Thus its Galois group modulo 3 contains an element of order 5.It is known that a Galois group modulo a prime is isomorphic to a subgroup of the Galois group over the rationals. A permutation group on 5 objects with elements of orders 6 and 5 must be the symmetric group
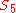 , which is therefore the Galois group of
, which is therefore the Galois group of  . This is one of the simplest examples of a non-solvable quintic polynomial. Serge Lang
. This is one of the simplest examples of a non-solvable quintic polynomial. Serge LangSerge Lang
Serge Lang was a French-born American mathematician. He was known for his work in number theory and for his mathematics textbooks, including the influential Algebra...
has said that Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
found this example.
The inverse Galois problem
All finite groups do occur as Galois groups. It is easy to construct field extensions with any given finite group as Galois group, as long as one does not also specify the ground fieldGround field
In mathematics, a ground field is a field K fixed at the beginning of the discussion. It is used in various areas of algebra: for example in linear algebra where the concept of a vector space may be developed over any field; and in algebraic geometry, where in the foundational developments of André...
.
For that, choose a field K and a finite group G. Cayley's theorem
Cayley's theorem
In group theory, Cayley's theorem, named in honor of Arthur Cayley, states that every group G is isomorphic to a subgroup of the symmetric group acting on G...
says that G is (up to isomorphism) a subgroup of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
S on the elements of G. Choose indeterminates {xα}, one for each element α of G, and adjoin them to K to get the field F = K({xα}). Contained within F is the field L of symmetric rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s in the {xα}. The Galois group of F/L is S, by a basic result of Emil Artin. G acts on F by restriction of action of S. If the fixed field of this action is M, then, by the fundamental theorem of Galois theory
Fundamental theorem of Galois theory
In mathematics, the fundamental theorem of Galois theory is a result that describes the structure of certain types of field extensions.In its most basic form, the theorem asserts that given a field extension E /F which is finite and Galois, there is a one-to-one correspondence between its...
, the Galois group of F/M is G.
It is an open problem to prove the existence of a field extension of the rational field Q with a given finite group as Galois group. Hilbert played a part in solving the problem for all symmetric and alternating groups. Igor Shafarevich
Igor Shafarevich
Igor Rostislavovich Shafarevich is a Soviet and Russian mathematician, founder of a school of algebraic number theory and algebraic geometry in the USSR, and a political writer. He was also an important dissident figure under the Soviet regime, a public supporter of Andrei Sakharov's Human Rights...
proved that every solvable finite group is the Galois group of some extension of Q. Various people have solved the inverse Galois problem for selected non-abelian simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
s. Existence of solutions has been shown for all but possibly one (Mathieu group
Mathieu group
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
M23) of the 26 sporadic simple groups. There is even a polynomial with integral coefficients whose Galois group is the Monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
.
See also
- Reed–Solomon error correctionReed–Solomon error correctionIn coding theory, Reed–Solomon codes are non-binary cyclic error-correcting codes invented by Irving S. Reed and Gustave Solomon. They described a systematic way of building codes that could detect and correct multiple random symbol errors...
- Differential Galois theoryDifferential Galois theoryIn mathematics, differential Galois theory studies the Galois groups of differential equations.Whereas algebraic Galois theory studies extensions of algebraic fields, differential Galois theory studies extensions of differential fields, i.e. fields that are equipped with a derivation, D. Much of...
- Grothendieck's Galois theoryGrothendieck's Galois theoryIn mathematics, Grothendieck's Galois theory is a highly abstract approach to the Galois theory of fields, developed around 1960 to provide a way to study the fundamental group of algebraic topology in the setting of algebraic geometry...
External links
Some on-line tutorials on Galois theory appear at:- http://www.math.niu.edu/~beachy/aaol/galois.html
- http://nrich.maths.org/public/viewer.php?obj_id=1422
- http://www.jmilne.org/math/CourseNotes/ft.html
Online textbooks in French, German, Italian and English can be found at:
- http://www.galois-group.net/

