Monomial
Encyclopedia
In mathematics
, in the context of polynomial
s, the word monomial can have one of two different meanings:
Both uses of this notion can be found, and in many cases the distinction is simply ignored, see for instance examples for the first and second meaning, and an unclear definition. In informal discussions the distinction is seldom important, and tendency is towards the broader second meaning. When studying the structure of polynomials however, one often definitely needs a notion with the first meaning. This is for instance the case when considering a monomial basis
of a polynomial ring
, or a monomial ordering of that basis. An argument in favor of the first meaning is also that no obvious other notion is available to designate these values (the term power product is in use, but it does not make the absence of constants clear either), while the notion term of a polynomial unambiguously coincides with the second meaning of monomial. For an isolated polynomial consisting of a single term, one could if necessary use the uncontracted form mononomial, analogous to binomial
and trinomial
.
The remainder of this article assumes the first meaning of "monomial".
of them, so they form a basis
of the vector space
of all polynomials - a fact of constant implicit use in mathematics.
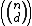. This expression can also be given in the form of a binomial coefficient
, as a polynomial expression
in d, or using a rising factorial power of :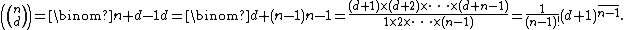
The latter forms are particularly useful when one fixes the number of variables and lets the degree vary. From these expressions one sees that for fixed n, the number of monomials of degree d is a polynomial expression in d of degree
with leading coefficient 
.
For example, the number of monomials in three variables (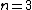
) of degree d is 
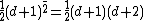; these numbers form the sequence 1, 3, 6, 10, 15, ... of triangular number
s.
s. If the variables being used form an indexed family like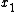
, 
, 
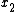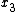, ..., then multi-index notation
is helpful: if we write
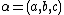
we can define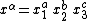
and save a great deal of space.
the varieties defined by monomial equations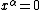
for some set of α have special properties of homogeneity. This can be phrased in the language of algebraic group
s, in terms of the existence of a group action
of an algebraic torus
(equivalently by a multiplicative group of diagonal matrices
). This area is studied under the name of torus embedding
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the context of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, the word monomial can have one of two different meanings:
- The first is a product of powers of variablesVariable (mathematics)In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
, or formally any value obtained by finitely many multiplications of a variable. If only a single variable
is considered, this means that any monomial is either 1 or a power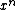 
of 
, with 
a positive integer. If several variables are considered, say, 
, 
, 
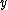, then each can be given an exponent, so that any monomial is of the form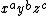 
with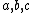 
non-negative integers (taking note that any exponent 0 makes the corresponding factor equal to 1). - The second meaning of monomial includes monomials in the first sense, but also allows multiplication by any constant, so that
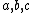and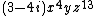 
are also considered to be monomials (the second example assuming polynomials in 
, 
, 
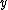over the complex numbers are considered).
Comparison of the two definitions
With either definition, the set of monomials is a subset of all polynomials that is closed under multiplication.Both uses of this notion can be found, and in many cases the distinction is simply ignored, see for instance examples for the first and second meaning, and an unclear definition. In informal discussions the distinction is seldom important, and tendency is towards the broader second meaning. When studying the structure of polynomials however, one often definitely needs a notion with the first meaning. This is for instance the case when considering a monomial basis
Monomial basis
In mathematics a monomial basis is a way to describe uniquely a polynomial using a linear combination of monomials. This description, the monomial form of a polynomial, is often used because of the simple structure of the monomial basis....
of a polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
, or a monomial ordering of that basis. An argument in favor of the first meaning is also that no obvious other notion is available to designate these values (the term power product is in use, but it does not make the absence of constants clear either), while the notion term of a polynomial unambiguously coincides with the second meaning of monomial. For an isolated polynomial consisting of a single term, one could if necessary use the uncontracted form mononomial, analogous to binomial
Binomial
In algebra, a binomial is a polynomial with two terms —the sum of two monomials—often bound by parenthesis or brackets when operated upon...
and trinomial
Trinomial
In elementary algebra, a trinomial is a polynomial consisting of three terms or monomials.-Trinomial expressions:# 3x + 5y + 8z with x, y, z variables# 3t + 9s^2 + 3y^3 with t, s, y variables# 3ts + 9t + 5s with t, s variables...
.
The remainder of this article assumes the first meaning of "monomial".
As bases
The most obvious fact about monomials (first meaning) is that any polynomial is a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of them, so they form a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of all polynomials - a fact of constant implicit use in mathematics.
Number
The number of monomials of degree d in n variables is the number of multicombinations of d elements chosen among the n variables (a variable can be chosen more than once, but order does not matter), which is given by the multiset coefficient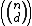. This expression can also be given in the form of a binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
, as a polynomial expression
Polynomial expression
In mathematics, and in particular in the field of algebra, a polynomial expression in one or more given entities E1, E2, ..., is any meaningful expression constructed from copies of those entities together with constants, using the operations of addition and multiplication...
in d, or using a rising factorial power of :
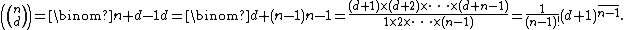
The latter forms are particularly useful when one fixes the number of variables and lets the degree vary. From these expressions one sees that for fixed n, the number of monomials of degree d is a polynomial expression in d of degree
with leading coefficient .For example, the number of monomials in three variables (
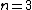) of degree d is 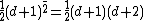; these numbers form the sequence 1, 3, 6, 10, 15, ... of triangular numberTriangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
s.
Notation
Notation for monomials is constantly required in fields like partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. If the variables being used form an indexed family like
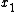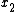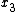, , , ..., then multi-index notationMulti-index notation
The mathematical notation of multi-indices simplifies formulae used in multivariable calculus, partial differential equations and the theory of distributions, by generalising the concept of an integer index to an ordered tuple of indices....
is helpful: if we write
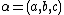
we can define
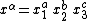
and save a great deal of space.
Geometry
In algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
the varieties defined by monomial equations
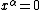for some set of α have special properties of homogeneity. This can be phrased in the language of algebraic groupAlgebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s, in terms of the existence of a group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of an algebraic torus
Algebraic torus
In mathematics, an algebraic torus is a type of commutative affine algebraic group. These groups were named by analogy with the theory of tori in Lie group theory...
(equivalently by a multiplicative group of diagonal matrices
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
). This area is studied under the name of torus embedding
Toric geometry
In algebraic geometry, a toric variety or torus embedding is a normal variety containing an algebraic torus as a dense subset, such that the action of the torus on itself extends to the whole variety.-The toric variety of a fan:...
s.
See also
- Monomial representationMonomial representationIn mathematics, a linear representation ρ of a group G is a monomial representation if there is a finite-index subgroup H and a one-dimensional linear representation σ of H, such that ρ is equivalent to the induced representation...
- Monomial matrixGeneralized permutation matrixIn mathematics, a generalized permutation matrix is a matrix with the same nonzero pattern as a permutation matrix, i.e. there is exactly one nonzero entry in each row and each column. Unlike a permutation matrix, where the nonzero entry must be 1, in a generalized permutation matrix the nonzero...
- Homogeneous polynomialHomogeneous polynomialIn mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
- Homogeneous functionHomogeneous functionIn mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
- Multilinear form