
Eudoxus of Cnidus
Encyclopedia
Eudoxus of Cnidus was a Greek
astronomer
, mathematician
, scholar and student of Plato
. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus
's poem on astronomy
. Theodosius of Bithynia's
Sphaerics may be based on a work of Eudoxus.
Εὔδοξος, from eu "good" and doxa "opinion, belief, fame"). It is analogous to the Latin name Benedictus
.
Eudoxus's father Aeschines of Cnidus loved to watch stars at night. Eudoxus first travelled to Tarentum
to study with Archytas
, from whom he learned mathematics
. While in Italy, Eudoxus visited Sicily, where he studied medicine with Philiston
.
Around 387 BC, at the age of 23, he traveled with the physician Theomedon, who according to Diogenes Laërtius
some believed was his lover, to Athens to study with the followers of Socrates
. He eventually became the pupil of Plato
, with whom he studied for several months, but due to a disagreement they had a falling out. Eudoxus was quite poor and could only afford an apartment at the Piraeus
. To attend Plato's lectures, he walked the seven miles (11 km) each direction, each day. Due to his poverty, his friends raised funds sufficient to send him to Heliopolis
, Egypt to pursue his study of astronomy and mathematics. He lived there for 16 months. From Egypt, he then traveled north to Cyzicus
, located on the south shore of the Sea of Marmara, and the Propontis. He traveled south to the court of Mausolus
. During his travels he gathered many students of his own.
Around 368 BC, Eudoxus returned to Athens with his students. According to some sources, around 367 he assumed headship of the Academy during Plato's period in Syracuse, and taught Aristotle. He eventually returned to his native Cnidus, where he served in the city assembly. While in Cnidus, he built an observatory and continued writing and lecturing on theology, astronomy and meteorology. He had one son, Aristagoras, and three daughters, Actis, Philtis and Delphis.
In mathematical astronomy, his fame is due to the introduction of the astronomical globe
, and his early contributions to understanding the movement of the planet
s.
His work on proportions
shows tremendous insight into number
s; it allows rigorous treatment of continuous quantities and not just whole numbers or even rational number
s. When it was revived by Tartaglia
and others in the 16th century, it became the basis for quantitative work in science for a century, until it was replaced by the algebraic methods of Descartes.
Eudoxus rigorously developed Antiphon
's method of exhaustion
, which was used in a masterly way by Archimedes
. This method is a precursor to the integral calculus.
An algebraic curve
(the Kampyle of Eudoxus) is named after him
Also, craters
on Mars and the Moon
are named in his honor.
had discovered that the diagonal of a square does not have a common unit of measurement with the sides of the square; this is the famous discovery that the square root of 2 cannot be expressed as the ratio of two integers. This discovery had heralded the existence of incommensurable quantities beyond the integers and rational fractions, but at the same time it threw into question the idea of measurement and calculations in geometry as a whole. For example, Euclid provides an elaborate proof of the Pythagorean theorem, by using addition of areas instead of the much simpler proof from similar triangles, which relies on ratios of line segments.
Ancient Greek mathematicians calculated not with quantities and equations as we do today, but instead they used proportionalities to express the relationship between quantities. Thus the ratio of two similar quantities was not just a numerical value, as we think of it today; the ratio of two similar quantities was a primitive relationship between them.
Eudoxus was able to restore confidence in the use of proportionalities by providing an astounding definition for the meaning of the equality between two ratios. This definition of proportion forms the subject of Euclid's Book V.
In Definition 5 of Euclid's Book V we read:
Let us clarify it by using modern-day notation. If we take four quantities: a, b, c, and d, then the first and second have a ratio ; similarly the third and fourth have a ratio
; similarly the third and fourth have a ratio 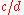 .
.
Now to say that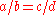 we do the following:
we do the following:
For any two arbitrary integers, m and n, form the equimultiples
m·a and m·c of the first and third; likewise form the equimultiples n·b and n·d of the second and fourth.
If it happens that m·a > n·b, then we must also have m·c > n·d.
If it happens that m·a = n·b, then we must also have m·c = n·d. Finally, if it happens that m·a < n·b, then we must also have m·c < n·d.
Notice that the definition depends on comparing the similar quantities m·a and n·b, and the similar quantities m·c and n·d, and does not depend on the existence of a common unit of measuring these quantities.
The complexity of the definition reflects the deep conceptual and methodological innovation involved. It brings to mind the famous fifth postulate of Euclid
concerning parallels, which is more extensive and complicated in its wording than the other postulates.
The Eudoxian definition of proportionality uses the quantifier, "for every ..." to harness the infinite and the infinitesimal, just as do the modern epsilon-delta definitions of limit and continuity.
Additionally, the Archimedean property
stated as definition 4 of Euclid's book V is originally due not to Archimedes but to Eudoxus.
, astronomy was a branch of mathematics; astronomers sought to create geometrical models that could imitate the appearances of celestial motions. Identifying the astronomical work of Eudoxus as a separate category is therefore a modern convenience. Some of Eudoxus' astronomical texts whose names have survived include:
We are fairly well informed about the contents of Phaenomena, for Eudoxus' prose text was the basis for a poem of the same name by Aratus
. Hipparchus
quoted from the text of Eudoxus in his commentary on Aratus.
Metaphysics XII, 8, and a commentary by Simplicius of Cilicia
(6th century CE) on De caelo, another work by Aristotle. According to a story reported by Simplicius, Plato posed a question for Greek astronomers: "By the assumption of what uniform and orderly motions can the apparent motions of the planets be accounted for?" (quoted in Lloyd 1970, p. 84). Plato proposed that the seemingly chaotic wandering motions of the planets could be explained by combinations of uniform circular motions centered on a spherical Earth, apparently a novel idea in the 4th century.
In most modern reconstructions of the Eudoxan model, the Moon is assigned three spheres:
The Sun is also assigned three spheres. The second completes its motion in a year instead of a month. The inclusion of a third sphere implies that Eudoxus mistakenly believed that the Sun had motion in latitude.
The five visible planets (Venus
, Mercury
, Mars
, Jupiter
, and Saturn
) are assigned four spheres each:
, a Greek astronomer of the 4th century, added seven spheres to Eudoxus' original 27 (in addition to the planetary spheres, Eudoxus included a sphere for the fixed stars). Aristotle described both systems, but insisted on adding "unrolling" spheres between each set of spheres to cancel the motions of the outer set. Aristotle was concerned about the physical nature of the system; without unrollers, the outer motions would be transferred to the inner planets.
A major flaw in the Eudoxan system is its inability to explain changes in the brightness of planets as seen from Earth. Because the spheres are concentric, planets will always remain at the same distance from Earth. This problem was pointed out in Antiquity by Autolycus of Pitane
. Astronomers responded by introducing the deferent and epicycle
, which caused a planet to vary its distance. However, Eudoxus' importance to Greek astronomy
is considerable, as he was the first to attempt a mathematical explanation of the planets.
, in The Nicomachean Ethics attributes to Eudoxus an argument in favor of hedonism
, that is, that pleasure is the ultimate good that activity strives for. According to Aristotle, Eudoxus put forward the following arguments for this position:
Ancient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
astronomer
Astronomer
An astronomer is a scientist who studies celestial bodies such as planets, stars and galaxies.Historically, astronomy was more concerned with the classification and description of phenomena in the sky, while astrophysics attempted to explain these phenomena and the differences between them using...
, mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, scholar and student of Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus
Aratus
Aratus was a Greek didactic poet. He is best known today for being quoted in the New Testament. His major extant work is his hexameter poem Phaenomena , the first half of which is a verse setting of a lost work of the same name by Eudoxus of Cnidus. It describes the constellations and other...
's poem on astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
. Theodosius of Bithynia's
Theodosius of Bithynia
Theodosius of Bithynia was a Greek astronomer and mathematician who wrote the Sphaerics, a book on the geometry of the sphere. Born in Tripolis, in Bithynia, Theodosius is cited by Vitruvius as having invented a sundial suitable for any place on Earth...
Sphaerics may be based on a work of Eudoxus.
Life
His name Eudoxus means "honored" or "of good repute" (in GreekGreek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
Εὔδοξος, from eu "good" and doxa "opinion, belief, fame"). It is analogous to the Latin name Benedictus
Benedictus
-Music:* Benedictus , the canticle sung at Lauds, also called the Canticle of Zachary.* The second part of the Sanctus, part of the eucharistic prayer* Benedictus , a song by Simon and Garfunkel...
.
Eudoxus's father Aeschines of Cnidus loved to watch stars at night. Eudoxus first travelled to Tarentum
Taranto
Taranto is a coastal city in Apulia, Southern Italy. It is the capital of the Province of Taranto and is an important commercial port as well as the main Italian naval base....
to study with Archytas
Archytas
Archytas was an Ancient Greek philosopher, mathematician, astronomer, statesman, and strategist. He was a scientist of the Pythagorean school and famous for being the reputed founder of mathematical mechanics, as well as a good friend of Plato....
, from whom he learned mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. While in Italy, Eudoxus visited Sicily, where he studied medicine with Philiston
Philistion of Locri
Philistion of Locri was a physician and writer on medicine who lived in the 4th century BC.He was a native of Locri in Italy, but was also referred to as "the Sicilian." He was tutor to the physician Chrysippus of Cnidos, and the astronomer and physician Eudoxus, and therefore must have lived in...
.
Around 387 BC, at the age of 23, he traveled with the physician Theomedon, who according to Diogenes Laërtius
Diogenes Laertius
Diogenes Laertius was a biographer of the Greek philosophers. Nothing is known about his life, but his surviving Lives and Opinions of Eminent Philosophers is one of the principal surviving sources for the history of Greek philosophy.-Life:Nothing is definitively known about his life...
some believed was his lover, to Athens to study with the followers of Socrates
Socrates
Socrates was a classical Greek Athenian philosopher. Credited as one of the founders of Western philosophy, he is an enigmatic figure known chiefly through the accounts of later classical writers, especially the writings of his students Plato and Xenophon, and the plays of his contemporary ...
. He eventually became the pupil of Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
, with whom he studied for several months, but due to a disagreement they had a falling out. Eudoxus was quite poor and could only afford an apartment at the Piraeus
Piraeus
Piraeus is a city in the region of Attica, Greece. Piraeus is located within the Athens Urban Area, 12 km southwest from its city center , and lies along the east coast of the Saronic Gulf....
. To attend Plato's lectures, he walked the seven miles (11 km) each direction, each day. Due to his poverty, his friends raised funds sufficient to send him to Heliopolis
Heliopolis (ancient)
Heliopolis was one of the oldest cities of ancient Egypt, the capital of the 13th Lower Egyptian nome that was located five miles east of the Nile to the north of the apex of the Nile Delta...
, Egypt to pursue his study of astronomy and mathematics. He lived there for 16 months. From Egypt, he then traveled north to Cyzicus
Cyzicus
Cyzicus was an ancient town of Mysia in Anatolia in the current Balıkesir Province of Turkey. It was located on the shoreward side of the present Kapıdağ Peninsula , a tombolo which is said to have originally been an island in the Sea of Marmara only to be connected to the mainland in historic...
, located on the south shore of the Sea of Marmara, and the Propontis. He traveled south to the court of Mausolus
Mausolus
Mausolus was ruler of Caria . He took part in the revolt against Artaxerxes Mnemon , conquered a great part of Lycia, Ionia and several Greek islands and cooperated with the Rhodians in the Social War against Athens...
. During his travels he gathered many students of his own.
Around 368 BC, Eudoxus returned to Athens with his students. According to some sources, around 367 he assumed headship of the Academy during Plato's period in Syracuse, and taught Aristotle. He eventually returned to his native Cnidus, where he served in the city assembly. While in Cnidus, he built an observatory and continued writing and lecturing on theology, astronomy and meteorology. He had one son, Aristagoras, and three daughters, Actis, Philtis and Delphis.
In mathematical astronomy, his fame is due to the introduction of the astronomical globe
Globe
A globe is a three-dimensional scale model of Earth or other spheroid celestial body such as a planet, star, or moon...
, and his early contributions to understanding the movement of the planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s.
His work on proportions
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
shows tremendous insight into number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s; it allows rigorous treatment of continuous quantities and not just whole numbers or even rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s. When it was revived by Tartaglia
Niccolò Fontana Tartaglia
Niccolò Fontana Tartaglia was a mathematician, an engineer , a surveyor and a bookkeeper from the then-Republic of Venice...
and others in the 16th century, it became the basis for quantitative work in science for a century, until it was replaced by the algebraic methods of Descartes.
Eudoxus rigorously developed Antiphon
Antiphon (person)
Antiphon the Sophist lived in Athens probably in the last two decades of the 5th century BC. There is an ongoing controversy over whether he is one and the same with Antiphon of the Athenian deme Rhamnus in Attica , the earliest of the ten Attic orators...
's method of exhaustion
Method of exhaustion
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
, which was used in a masterly way by Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
. This method is a precursor to the integral calculus.
An algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
(the Kampyle of Eudoxus) is named after him
- a2x4 = b4(x2 + y2).
Also, craters
Impact crater
In the broadest sense, the term impact crater can be applied to any depression, natural or manmade, resulting from the high velocity impact of a projectile with a larger body...
on Mars and the Moon
Eudoxus (lunar crater)
Eudoxus is a prominent lunar impact crater that lies to the east of the northern tip of the Montes Caucasus range. It is located to the south of the prominent crater Aristoteles in the northern regions of the visible Moon...
are named in his honor.
Mathematics
The PythagoreansPythagoreanism
Pythagoreanism was the system of esoteric and metaphysical beliefs held by Pythagoras and his followers, the Pythagoreans, who were considerably influenced by mathematics. Pythagoreanism originated in the 5th century BCE and greatly influenced Platonism...
had discovered that the diagonal of a square does not have a common unit of measurement with the sides of the square; this is the famous discovery that the square root of 2 cannot be expressed as the ratio of two integers. This discovery had heralded the existence of incommensurable quantities beyond the integers and rational fractions, but at the same time it threw into question the idea of measurement and calculations in geometry as a whole. For example, Euclid provides an elaborate proof of the Pythagorean theorem, by using addition of areas instead of the much simpler proof from similar triangles, which relies on ratios of line segments.
Ancient Greek mathematicians calculated not with quantities and equations as we do today, but instead they used proportionalities to express the relationship between quantities. Thus the ratio of two similar quantities was not just a numerical value, as we think of it today; the ratio of two similar quantities was a primitive relationship between them.
Eudoxus was able to restore confidence in the use of proportionalities by providing an astounding definition for the meaning of the equality between two ratios. This definition of proportion forms the subject of Euclid's Book V.
In Definition 5 of Euclid's Book V we read:
Let us clarify it by using modern-day notation. If we take four quantities: a, b, c, and d, then the first and second have a ratio
 ; similarly the third and fourth have a ratio
; similarly the third and fourth have a ratio 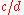 .
.Now to say that
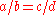 we do the following:
we do the following:For any two arbitrary integers, m and n, form the equimultiples
m·a and m·c of the first and third; likewise form the equimultiples n·b and n·d of the second and fourth.
If it happens that m·a > n·b, then we must also have m·c > n·d.
If it happens that m·a = n·b, then we must also have m·c = n·d. Finally, if it happens that m·a < n·b, then we must also have m·c < n·d.
Notice that the definition depends on comparing the similar quantities m·a and n·b, and the similar quantities m·c and n·d, and does not depend on the existence of a common unit of measuring these quantities.
The complexity of the definition reflects the deep conceptual and methodological innovation involved. It brings to mind the famous fifth postulate of Euclid
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
concerning parallels, which is more extensive and complicated in its wording than the other postulates.
The Eudoxian definition of proportionality uses the quantifier, "for every ..." to harness the infinite and the infinitesimal, just as do the modern epsilon-delta definitions of limit and continuity.
Additionally, the Archimedean property
Archimedean property
In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some ordered or normed groups, fields, and other algebraic structures. Roughly speaking, it is the property of having no infinitely large or...
stated as definition 4 of Euclid's book V is originally due not to Archimedes but to Eudoxus.
Astronomy
In ancient GreeceAncient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
, astronomy was a branch of mathematics; astronomers sought to create geometrical models that could imitate the appearances of celestial motions. Identifying the astronomical work of Eudoxus as a separate category is therefore a modern convenience. Some of Eudoxus' astronomical texts whose names have survived include:
- Disappearances of the Sun, possibly on eclipses
- Oktaeteris (Ὀκταετηρίς), on an eight-year lunisolar cycle of the calendar
- Phaenomena (Φαινόμενα) and Entropon (Ἔντροπον), on spherical astronomySpherical astronomySpherical astronomy or positional astronomy is the branch of astronomy that is used to determine the location of objects on the celestial sphere, as seen at a particular date, time, and location on the Earth. It relies on the mathematical methods of spherical geometry and the measurements of...
, probably based on observations made by Eudoxus in Egypt and Cnidus - On Speeds, on planetary motions
We are fairly well informed about the contents of Phaenomena, for Eudoxus' prose text was the basis for a poem of the same name by Aratus
Aratus
Aratus was a Greek didactic poet. He is best known today for being quoted in the New Testament. His major extant work is his hexameter poem Phaenomena , the first half of which is a verse setting of a lost work of the same name by Eudoxus of Cnidus. It describes the constellations and other...
. Hipparchus
Hipparchus
Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
quoted from the text of Eudoxus in his commentary on Aratus.
Eudoxan planetary models
A general idea of the content of On Speeds can be gleaned from Aristotle'sAristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
Metaphysics XII, 8, and a commentary by Simplicius of Cilicia
Simplicius of Cilicia
Simplicius of Cilicia, was a disciple of Ammonius Hermiae and Damascius, and was one of the last of the Neoplatonists. He was among the pagan philosophers persecuted by Justinian in the early 6th century, and was forced for a time to seek refuge in the Persian court, before being allowed back into...
(6th century CE) on De caelo, another work by Aristotle. According to a story reported by Simplicius, Plato posed a question for Greek astronomers: "By the assumption of what uniform and orderly motions can the apparent motions of the planets be accounted for?" (quoted in Lloyd 1970, p. 84). Plato proposed that the seemingly chaotic wandering motions of the planets could be explained by combinations of uniform circular motions centered on a spherical Earth, apparently a novel idea in the 4th century.
In most modern reconstructions of the Eudoxan model, the Moon is assigned three spheres:
- The outermost rotates westward once in 24 hours, explaining rising and setting.
- The second rotates eastward once in a month, explaining the monthly motion of the Moon through the zodiacZodiacIn astronomy, the zodiac is a circle of twelve 30° divisions of celestial longitude which are centred upon the ecliptic: the apparent path of the Sun across the celestial sphere over the course of the year...
. - The third also completes its revolution in a month, but its axis is tilted at a slightly different angle, explaining motion in latitude (deviation from the eclipticEclipticThe ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
), and the motion of the lunar nodeLunar nodeThe lunar nodes are the orbital nodes of the Moon, that is, the points where the orbit of the Moon crosses the ecliptic . The ascending node is where the moon crosses to the north of the ecliptic...
s.
The Sun is also assigned three spheres. The second completes its motion in a year instead of a month. The inclusion of a third sphere implies that Eudoxus mistakenly believed that the Sun had motion in latitude.
The five visible planets (Venus
Venus
Venus is the second planet from the Sun, orbiting it every 224.7 Earth days. The planet is named after Venus, the Roman goddess of love and beauty. After the Moon, it is the brightest natural object in the night sky, reaching an apparent magnitude of −4.6, bright enough to cast shadows...
, Mercury
Mercury (planet)
Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits...
, Mars
Mars
Mars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance...
, Jupiter
Jupiter
Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,...
, and Saturn
Saturn
Saturn is the sixth planet from the Sun and the second largest planet in the Solar System, after Jupiter. Saturn is named after the Roman god Saturn, equated to the Greek Cronus , the Babylonian Ninurta and the Hindu Shani. Saturn's astronomical symbol represents the Roman god's sickle.Saturn,...
) are assigned four spheres each:
- The outermost explains the daily motion.
- The second explains the planet's motion through the zodiac.
- The third and fourth together explain retrogradation, when a planet appears to slow down, then briefly reverse its motion through the zodiac. By inclining the axes of the two spheres with respect to each other, and rotating them in opposite directions but with equal periods, Eudoxus could make a point on the inner sphere trace out a figure-eight shape, or hippopedeHippopedeIn geometry, a hippopede is a plane curve determined by an equation of the form^2=cx^2+dy^2,...
.
Importance of Eudoxan system
CallippusCallippus
Callippus or Calippus was a Greek astronomer and mathematician.Callippus was born at Cyzicus, and studied under Eudoxus of Cnidus at the Academy of Plato. He also worked with Aristotle at the Lyceum, which means that he was active in Athens prior to Aristotle's death in 322...
, a Greek astronomer of the 4th century, added seven spheres to Eudoxus' original 27 (in addition to the planetary spheres, Eudoxus included a sphere for the fixed stars). Aristotle described both systems, but insisted on adding "unrolling" spheres between each set of spheres to cancel the motions of the outer set. Aristotle was concerned about the physical nature of the system; without unrollers, the outer motions would be transferred to the inner planets.
A major flaw in the Eudoxan system is its inability to explain changes in the brightness of planets as seen from Earth. Because the spheres are concentric, planets will always remain at the same distance from Earth. This problem was pointed out in Antiquity by Autolycus of Pitane
Autolycus of Pitane
Autolycus of Pitane was a Greek astronomer, mathematician, and geographer. The lunar crater Autolycus was named in his honour.- Life and work :Autolycus was born in Pitane, a town of Aeolis within Western Anatolia...
. Astronomers responded by introducing the deferent and epicycle
Deferent and epicycle
In the Ptolemaic system of astronomy, the epicycle was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon, Sun, and planets...
, which caused a planet to vary its distance. However, Eudoxus' importance to Greek astronomy
Greek astronomy
Greek astronomy is astronomy written in the Greek language in classical antiquity. Greek astronomy is understood to include the ancient Greek, Hellenistic, Greco-Roman, and Late Antiquity eras. It is not limited geographically to Greece or to ethnic Greeks, as the Greek language had become the...
is considerable, as he was the first to attempt a mathematical explanation of the planets.
Ethics
AristotleAristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
, in The Nicomachean Ethics attributes to Eudoxus an argument in favor of hedonism
Hedonism
Hedonism is a school of thought which argues that pleasure is the only intrinsic good. In very simple terms, a hedonist strives to maximize net pleasure .-Etymology:The name derives from the Greek word for "delight" ....
, that is, that pleasure is the ultimate good that activity strives for. According to Aristotle, Eudoxus put forward the following arguments for this position:
- All things, rational and irrational, aim at pleasure; things aim at what they believe to be good; a good indication of what the chief good is would be the thing that most things aim at.
- Similarly, pleasure's opposite − pain − is universally avoided, which provides additional support for the idea that pleasure is universally considered good.
- People don't seek pleasure as a means to something else, but as an end in its own right.
- Any other good that you can think of would be better if pleasure were added to it, and it is only by good that good can be increased.
- Of all of the things that are good, happiness is peculiar for not being praised, which may show that it is the crowning good.
External links
- Models of Planetary Motion—Eudoxus
- The Universe According to Eudoxus (JavaJava Virtual MachineA Java virtual machine is a virtual machine capable of executing Java bytecode. It is the code execution component of the Java software platform. Sun Microsystems stated that there are over 4.5 billion JVM-enabled devices.-Overview:...
applet) - Eudoxus of Cnidus
- Application of mathematical principles associated with Eudoxus
- Herodotus Project: Extensive B+W photo essay of Cnidus
- Dennis Duke, "Statistical dating of the Phaenomena of Eudoxus", DIO, volume 15, pages 7 to 23.

