Characteristic class
Encyclopedia
In mathematics
, a characteristic class is a way of associating to each principal bundle
on a topological space
X a cohomology
class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses section
s or not. In other words, characteristic classes are global invariants which measure the deviation of a local product structure from a global product structure. They are one of the unifying geometric concepts in algebraic topology
, differential geometry and algebraic geometry
.
, and for a topological space X, write bG(X) for the set of isomorphism class
es of principal G-bundles
. This bG is a contravariant functor
from Top (the category
of topological spaces and continuous function
s) to Set (the category of sets and function
s), sending a map f to the pullback
operation f*.
A characteristic class c of principal G-bundles is then a natural transformation
from bG to a cohomology functor H*, regarded also as a functor to Set.
In other words, a characteristic class associates to any principal G-bundle P → X an element c(P) in H*(X) such that, if f : Y → X is a continuous map, then c(f*P) = f*c(P). On the left is the class of the pullback of P to Y; on the right is the image of the class of P under the induced map in cohomology.
Stiefel-Whitney numbers,
Chern numbers, Pontryagin numbers, and the
Euler characteristic.
Given an oriented manifold M of dimension n with fundamental class
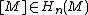, and a G-bundle with characteristic classes 
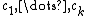, one can pair a product of characteristic classes of total degree n with the fundamental class. The number of distinct characteristic numbers is the number of monomial
s of degree n in the characteristic classes, or equivalently the partitions of n into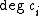
.
Formally, given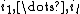
such that 
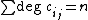, the corresponding characteristic number is: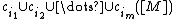
These are notated various as either the product of characteristic classes, such as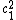
or by some alternative notation, such as 
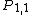for the Pontryagin number corresponding to 
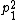, or 
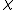for the Euler characteristic.
From the point of view of de Rham cohomology
, one can take differential form
s representing the characteristic classes, take a wedge product so that one obtains a top dimensional form, then integrates over the manifold; this is analogous to taking the product in cohomology and pairing with the fundamental class.
This also works for non-orientable manifolds, which have a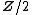
-orientation, in which case one obtains 
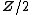-valued characteristic numbers, such as the Stiefel-Whitney numbers.
Characteristic numbers solve the oriented and unoriented bordism questions: two manifolds are (respectively oriented or unoriented) cobordant if and only if their characteristic numbers are equal.
is a kind of function on a space, and to lead to a contradiction from the existence of a section we do need that variance. In fact cohomology theory grew up after homology
and homotopy theory, which are both covariant theories based on mapping into a space; and characteristic class theory in its infancy in the 1930s (as part of obstruction theory
) was one major reason why a 'dual' theory to homology was sought. The characteristic class approach to curvature
invariants was a particular reason to make a theory, to prove a general Gauss-Bonnet theorem.
When the theory was put on an organised basis around 1950 (with the definitions reduced to homotopy theory) it became clear that the most fundamental characteristic classes known at that time (the Stiefel-Whitney class, the Chern class
, and the Pontryagin class
es) were reflections of the classical linear groups and their maximal torus
structure. What is more, the Chern class itself was not so new, having been reflected in the Schubert calculus
on Grassmannian
s, and the work of the Italian school of algebraic geometry
. On the other hand there was now a framework which produced families of classes, whenever there was a vector bundle
involved.
The prime mechanism then appeared to be this: Given a space X carrying a vector bundle, that implied in the homotopy category
a mapping from X to a classifying space
BG, for the relevant linear group G. For the homotopy theory the relevant information is carried by compact subgroups such as the orthogonal group
s and unitary group
s of G. Once the cohomology H*(BG) was calculated, once and for all, the contravariance property of cohomology meant that characteristic classes for the bundle would be defined in H*(X) in the same dimensions. For example the Chern class
is really one class with graded components in each even dimension.
This is still the classic explanation, though in a given geometric theory it is profitable to take extra structure into account. When cohomology became 'extraordinary' with the arrival of K-theory
and cobordism theory from 1955 onwards, it was really only necessary to change the letter H everywhere to say what the characteristic classes were.
Characteristic classes were later found for foliation
s of manifold
s; they have (in a modified sense, for foliations with some allowed singularities) a classifying space theory in homotopy
theory.
In later work after the reapprochement of mathematics and physics
, new characteristic classes were found by Simon Donaldson
and Dieter Kotschick in the instanton
theory. The work and point of view of Chern
have also proved important: see Chern-Simons theory.
, the Chern class
, Stiefel-Whitney class, and Pontryagin class
are stable, while the Euler class
is unstable.
Concretely, a stable class is one that does not change when one adds a trivial bundle: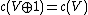
. More abstractly, it means that the cohomology class in the classifying space
for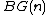
pulls back from the cohomology class in 
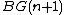under the inclusion 
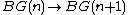(which corresponds to the inclusion 
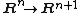and similar). Equivalently, all finite characteristic classes pull back from a stable class in 
.
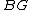This is not the case for the Euler class, as detailed there, not least because the Euler class of a k-dimensional bundle lives in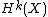
(hence pulls back from 
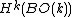, so it can’t pull back from a class in 
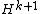, as the dimensions differ.
From the perspective of the splitting principle
, this corresponds to the stability of symmetric polynomials, and the instability of alternating polynomials, specifically the Vandermonde polynomial, which represents the Euler class.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a characteristic class is a way of associating to each principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
on a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X a cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses section
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
s or not. In other words, characteristic classes are global invariants which measure the deviation of a local product structure from a global product structure. They are one of the unifying geometric concepts in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, differential geometry and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.
Definition
Let G be a topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
, and for a topological space X, write bG(X) for the set of isomorphism class
Isomorphism class
An isomorphism class is a collection of mathematical objects isomorphic to each other.Isomorphism classes are often defined if the exact identity of the elements of the set is considered irrelevant, and the properties of the structure of the mathematical object are studied. Examples of this are...
es of principal G-bundles
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
. This bG is a contravariant functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from Top (the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of topological spaces and continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s) to Set (the category of sets and function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s), sending a map f to the pullback
Pullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
operation f*.
A characteristic class c of principal G-bundles is then a natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
from bG to a cohomology functor H*, regarded also as a functor to Set.
In other words, a characteristic class associates to any principal G-bundle P → X an element c(P) in H*(X) such that, if f : Y → X is a continuous map, then c(f*P) = f*c(P). On the left is the class of the pullback of P to Y; on the right is the image of the class of P under the induced map in cohomology.
Characteristic numbers
Characteristic classes are elements of cohomology groups; one can obtain integers from characteristic classes, called characteristic numbers. Respectively:Stiefel-Whitney numbers,
Chern numbers, Pontryagin numbers, and the
Euler characteristic.
Given an oriented manifold M of dimension n with fundamental class
Fundamental class
In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
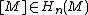, and a G-bundle with characteristic classes 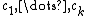, one can pair a product of characteristic classes of total degree n with the fundamental class. The number of distinct characteristic numbers is the number of monomialMonomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s of degree n in the characteristic classes, or equivalently the partitions of n into
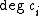.Formally, given
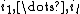such that 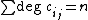, the corresponding characteristic number is: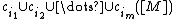These are notated various as either the product of characteristic classes, such as
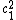or by some alternative notation, such as 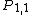for the Pontryagin number corresponding to 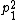, or 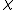for the Euler characteristic.From the point of view of de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
, one can take differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s representing the characteristic classes, take a wedge product so that one obtains a top dimensional form, then integrates over the manifold; this is analogous to taking the product in cohomology and pairing with the fundamental class.
This also works for non-orientable manifolds, which have a
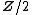-orientation, in which case one obtains 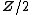-valued characteristic numbers, such as the Stiefel-Whitney numbers.Characteristic numbers solve the oriented and unoriented bordism questions: two manifolds are (respectively oriented or unoriented) cobordant if and only if their characteristic numbers are equal.
Motivation
Characteristic classes are in an essential way phenomena of cohomology theory — they are contravariant constructions, in the way that a sectionSection (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
is a kind of function on a space, and to lead to a contradiction from the existence of a section we do need that variance. In fact cohomology theory grew up after homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
and homotopy theory, which are both covariant theories based on mapping into a space; and characteristic class theory in its infancy in the 1930s (as part of obstruction theory
Obstruction theory
In mathematics, obstruction theory is a name given to two different mathematical theories, both of which yield cohomological invariants.-In homotopy theory:...
) was one major reason why a 'dual' theory to homology was sought. The characteristic class approach to curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
invariants was a particular reason to make a theory, to prove a general Gauss-Bonnet theorem.
When the theory was put on an organised basis around 1950 (with the definitions reduced to homotopy theory) it became clear that the most fundamental characteristic classes known at that time (the Stiefel-Whitney class, the Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
, and the Pontryagin class
Pontryagin class
In mathematics, the Pontryagin classes are certain characteristic classes. The Pontryagin class lies in cohomology groups with degree a multiple of four...
es) were reflections of the classical linear groups and their maximal torus
Maximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
structure. What is more, the Chern class itself was not so new, having been reflected in the Schubert calculus
Schubert calculus
In mathematics, Schubert calculus is a branch of algebraic geometry introduced in the nineteenth century by Hermann Schubert, in order to solve various counting problems of projective geometry...
on Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
s, and the work of the Italian school of algebraic geometry
Italian school of algebraic geometry
In relation with the history of mathematics, the Italian school of algebraic geometry refers to the work over half a century or more done internationally in birational geometry, particularly on algebraic surfaces. There were in the region of 30 to 40 leading mathematicians who made major...
. On the other hand there was now a framework which produced families of classes, whenever there was a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
involved.
The prime mechanism then appeared to be this: Given a space X carrying a vector bundle, that implied in the homotopy category
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
a mapping from X to a classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
BG, for the relevant linear group G. For the homotopy theory the relevant information is carried by compact subgroups such as the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
s and unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
s of G. Once the cohomology H*(BG) was calculated, once and for all, the contravariance property of cohomology meant that characteristic classes for the bundle would be defined in H*(X) in the same dimensions. For example the Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
is really one class with graded components in each even dimension.
This is still the classic explanation, though in a given geometric theory it is profitable to take extra structure into account. When cohomology became 'extraordinary' with the arrival of K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
and cobordism theory from 1955 onwards, it was really only necessary to change the letter H everywhere to say what the characteristic classes were.
Characteristic classes were later found for foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
s of manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s; they have (in a modified sense, for foliations with some allowed singularities) a classifying space theory in homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
theory.
In later work after the reapprochement of mathematics and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, new characteristic classes were found by Simon Donaldson
Simon Donaldson
Simon Kirwan Donaldson FRS , is an English mathematician known for his work on the topology of smooth four-dimensional manifolds. He is now Royal Society research professor in Pure Mathematics and President of the Institute for Mathematical Science at Imperial College London...
and Dieter Kotschick in the instanton
Instanton
An instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
theory. The work and point of view of Chern
Shiing-Shen Chern
Shiing-Shen Chern was a Chinese American mathematician, one of the leaders in differential geometry of the twentieth century.-Early years in China:...
have also proved important: see Chern-Simons theory.
Stability
In the language of stable homotopy theoryStable homotopy theory
In mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...
, the Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
, Stiefel-Whitney class, and Pontryagin class
Pontryagin class
In mathematics, the Pontryagin classes are certain characteristic classes. The Pontryagin class lies in cohomology groups with degree a multiple of four...
are stable, while the Euler class
Euler class
In mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
is unstable.
Concretely, a stable class is one that does not change when one adds a trivial bundle:
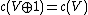. More abstractly, it means that the cohomology class in the classifying spaceClassifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
for
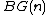pulls back from the cohomology class in 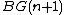under the inclusion 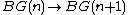(which corresponds to the inclusion 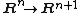and similar). Equivalently, all finite characteristic classes pull back from a stable class in 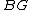.This is not the case for the Euler class, as detailed there, not least because the Euler class of a k-dimensional bundle lives in
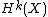(hence pulls back from 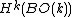, so it can’t pull back from a class in 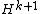, as the dimensions differ.From the perspective of the splitting principle
Splitting principle
In mathematics, the splitting principle is a technique used to reduce questions about vector bundles to the case of line bundles.In the theory of vector bundles, one often wishes to simplify computations, say of Chern classes. Often computations are well understood for line bundles and for direct...
, this corresponds to the stability of symmetric polynomials, and the instability of alternating polynomials, specifically the Vandermonde polynomial, which represents the Euler class.
See also
- Chern classChern classIn mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
- Segre classSegre classIn mathematics, the Segre class is a characteristic class used in the study of singular vector bundles. The total Segre class is inverse to the total Chern class, and thus provides equivalent information; the advantage of the Segre class is that it generalizes to singular vector bundles, while the...
- Stiefel-Whitney class
- Pontryagin classPontryagin classIn mathematics, the Pontryagin classes are certain characteristic classes. The Pontryagin class lies in cohomology groups with degree a multiple of four...
- Euler classEuler classIn mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...