
Squaring the circle
Encyclopedia
Squaring the circle is a problem proposed by ancient
geometers. It is the challenge of constructing a square
with the same area as a given circle
by using only a finite number of steps with compass and straightedge
. More abstractly and more precisely, it may be taken to ask whether specified axiom
s of Euclidean geometry
concerning the existence of lines and circles entail the existence of such a square.
In 1882, the task was proven to be impossible, as a consequence of the Lindemann–Weierstrass theorem
which proves that pi
is a transcendental
, rather than an algebraic irrational number; that is, it is not the root of any polynomial
with rational coefficients. It had been known for some decades before then that if pi were transcendental then the construction would be impossible, but that pi is transcendental was not proven until 1882. Approximate squaring to any given non-perfect accuracy, in contrast, is possible in a finite number of steps, since there are rational numbers arbitrarily close to pi.
The expression "squaring the circle" is sometimes used as a metaphor for doing something logically or intuitively impossible.
The term quadrature
of the circle is sometimes used synonymously, or may refer to approximate or numerical methods for finding the area of a circle.
. The Egyptian Rhind papyrus of 1800BC gives the area of a circle as (64/81) 2, where is the diameter of the circle, and pi approximated to 256/81, a number that appears in the older Moscow Mathematical Papyrus, and used for volume approximations (i.e. hekat (volume unit)). Indian mathematicians
also found an approximate method, though less accurate, documented in the Sulba Sutras
. Archimedes
showed that the value of pi lay between 3 + 1/7 (approximately 3.1429) and 3 + 10/71 (approximately 3.1408). See Numerical approximations of π
for more on the history.
The first Greek to be associated with the problem was Anaxagoras
, who worked on it while in prison. Hippocrates of Chios
squared certain lunes
, in the hope that it would lead to a solution — see Lune of Hippocrates
. Antiphon the Sophist believed that inscribing regular polygons within a circle and doubling the number of sides will eventually fill up the area of the circle, and since a polygon can be squared, it means the circle can be squared. Even then there were skeptics—Eudemus argued that magnitudes cannot be divided up without limit, so the area of the circle will never be used up. The problem was even mentioned in Aristophanes
's play The Birds
.
It is believed that Oenopides
was the first Greek who required a plane solution (that is, using only a compass and straightedge). James Gregory
attempted a proof of its impossibility in Vera Circuli et Hyperbolae Quadratura (The True Squaring of the Circle and of the Hyperbola) in 1667. Although his proof was incorrect, it was the first paper to attempt to solve the problem using algebraic properties of pi. It was not until 1882 that Ferdinand von Lindemann
rigorously proved its impossibility.
 The famous Victorian-age mathematician, logician and author, Charles Lutwidge Dodgson
The famous Victorian-age mathematician, logician and author, Charles Lutwidge Dodgson
(better known under the pseudonym, "Lewis Carroll") also expressed interest in debunking illogical circle-squaring theories. In one of his diary entries for 1855, Dodgson listed books he hoped to write including one called "Plain Facts for Circle-Squarers". In the introduction to "A New Theory of Parallels", Dodgson recounted an attempt to demonstrate logical errors to a couple of circle-squarers, stating:
 , and the impossibility of this undertaking follows from the fact that pi is a transcendental
, and the impossibility of this undertaking follows from the fact that pi is a transcendental
(non-algebraic
and therefore non-constructible
) number. If the problem of the quadrature of the circle is solved using only compass and straightedge, then an algebraic value of pi would be found, which is impossible. Johann Heinrich Lambert
conjectured that pi was transcendental in 1768 in the same paper he proved its irrationality, even before the existence of transcendental numbers was proven. It was not until 1882 that Ferdinand von Lindemann
proved its transcendence.
The transcendence of pi implies the impossibility of exactly "circling" the square, as well as of squaring the circle.
It is possible to construct a square with an area arbitrarily close to that of a given circle. If a rational number is used as an approximation of pi, then squaring the circle becomes possible, depending on the values chosen. However, this is only an approximation and does not meet the constraints of the ancient rules for solving the problem. Several mathematicians have demonstrated workable procedures based on a variety of approximations.
Bending the rules by allowing an infinite number of compass-and-straightedge operations or by performing the operations on certain non-Euclidean space
s also makes squaring the circle possible. For example, although the circle cannot be squared in Euclidean space, it can be in Gauss–Bolyai–Lobachevsky space
. Indeed, even the preceding phrase is overoptimistic. There are no squares as such in the hyperbolic plane, although there are regular quadrilaterals, meaning quadrilaterals with all sides congruent and all angles congruent (but these angles are strictly smaller than right angles).
There exist, in the hyperbolic plane, (countably) infinitely many pairs of constructible circles and constructible regular quadrilaterals of equal area.
However, there is no method for starting with a regular quadrilateral and constructing the circle of equal area, and there is no method for starting with a circle and constructing a regular quadrilateral of equal area (even when the circle has small enough radius such that a regular quadrilateral of equal area exists).
It takes only minimal knowledge of elementary geometry to convert any given rational approximation of pi into a corresponding compass-and-straightedge construction, but constructions made in this way tend to be very long-winded in comparison to the accuracy they achieve. After the exact problem was proven unsolvable, some mathematicians applied their ingenuity to finding elegant approximations to squaring the circle, defined roughly and informally as constructions that are particularly simple among other imaginable constructions that give similar precision.
Among the modern approximate constructions was one by E. W. Hobson
in 1913 (see his book). This was a fairly accurate construction which was based on constructing the approximate value of 3.14164079..., which is accurate to 4 decimals (i.e. it differs from pi by about ).
Indian mathematician Srinivasa Ramanujan
in 1913, C. D. Olds in 1963, Martin Gardner
in 1966, and Benjamin Bold in 1982 all gave geometric constructions for
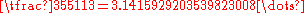
which is accurate to six decimal places of pi.
 Srinivasa Ramanujan in 1914 gave a ruler-and-compass construction which was equivalent to taking the approximate value for pi to be
Srinivasa Ramanujan in 1914 gave a ruler-and-compass construction which was equivalent to taking the approximate value for pi to be
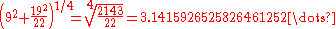
giving a remarkable eight decimal places of pi.
In 1991, Robert Dixon
gave constructions for
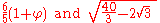
(Kochański's approximation), though these were only accurate to four decimal places of pi.
in calculus
, or quadrature in numerical analysis
, was known as squaring before the invention of calculus. Since the techniques of calculus were unknown, it was generally presumed that a squaring should be done via geometric constructions, that is, by compass and straightedge. For example Newton
wrote to Oldenberg in 1676 "I believe M. Leibnitz will not dislike the Theorem towards the beginning of my letter pag. 4 for squaring Curve lines Geometrically" (emphasis added). After Newton and Leibniz
invented calculus, they still referred to this integration problem as squaring a curve.
For example, in Spanish, the expression "descubriste la cuadratura del círculo" ("you discovered the quadrature of the circle") is often used derisively to dismiss claims that someone has found a simple solution to a particularly hard or intractable problem.
of the circle is impossible using only compass and straightedge has not proved to be a hindrance to the many people who have invested years in this problem anyway. Having squared the circle is a famous crank
assertion. (See also pseudomathematics
.) In his old age, the English philosopher Thomas Hobbes
convinced himself that he had succeeded in squaring the circle.
During the 18th and 19th century the notion that the problem of squaring the circle was somehow related to the longitude problem
seems to have become prevalent among would-be circle squarers. Using "cyclometer" for circle-squarer, Augustus de Morgan
wrote in 1872:
Although from 1714 to 1828 the British government did indeed sponsor a £20,000 prize
for finding a solution to the longitude problem, exactly why the connection was made to squaring the circle is not clear; especially since two non-geometric methods (the astronomical method of lunar distances
and the mechanical chronometer
) had been found by the late 1760s. De Morgan goes on to say that "[t]he longitude problem in no way depends upon perfect solution; existing approximations are sufficient to a point of accuracy far beyond what can be wanted." In his book, de Morgan also mentions receiving many threatening letters from would-be circle squarers, accusing him of trying to "cheat them out of their prize."
Classical antiquity
Classical antiquity is a broad term for a long period of cultural history centered on the Mediterranean Sea, comprising the interlocking civilizations of ancient Greece and ancient Rome, collectively known as the Greco-Roman world...
geometers. It is the challenge of constructing a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
with the same area as a given circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
by using only a finite number of steps with compass and straightedge
Compass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
. More abstractly and more precisely, it may be taken to ask whether specified axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s of Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
concerning the existence of lines and circles entail the existence of such a square.
In 1882, the task was proven to be impossible, as a consequence of the Lindemann–Weierstrass theorem
Lindemann–Weierstrass theorem
In mathematics, the Lindemann–Weierstrass theorem is a result that is very useful in establishing the transcendence of numbers. It states that if 1, ..., are algebraic numbers which are linearly independent over the rational numbers ', then 1, ..., are algebraically...
which proves that pi
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
is a transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
, rather than an algebraic irrational number; that is, it is not the root of any polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with rational coefficients. It had been known for some decades before then that if pi were transcendental then the construction would be impossible, but that pi is transcendental was not proven until 1882. Approximate squaring to any given non-perfect accuracy, in contrast, is possible in a finite number of steps, since there are rational numbers arbitrarily close to pi.
The expression "squaring the circle" is sometimes used as a metaphor for doing something logically or intuitively impossible.
The term quadrature
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
of the circle is sometimes used synonymously, or may refer to approximate or numerical methods for finding the area of a circle.
History
Methods to approximate the area of a given circle with a square were known already to Babylonian mathematiciansBabylonian mathematics
Babylonian mathematics refers to any mathematics of the people of Mesopotamia, from the days of the early Sumerians to the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited...
. The Egyptian Rhind papyrus of 1800BC gives the area of a circle as (64/81) 2, where is the diameter of the circle, and pi approximated to 256/81, a number that appears in the older Moscow Mathematical Papyrus, and used for volume approximations (i.e. hekat (volume unit)). Indian mathematicians
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
also found an approximate method, though less accurate, documented in the Sulba Sutras
Sulba Sutras
The Shulba Sutras or Śulbasūtras are sutra texts belonging to the Śrauta ritual and containing geometry related to fire-altar construction.- Purpose and origins :...
. Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
showed that the value of pi lay between 3 + 1/7 (approximately 3.1429) and 3 + 10/71 (approximately 3.1408). See Numerical approximations of π
Numerical approximations of π
This page is about the history of approximations for the mathematical constant pi . There is a table summarizing the chronology of computation of π. See also the history of pi for other aspects of the evolution of our knowledge about mathematical properties of pi...
for more on the history.
The first Greek to be associated with the problem was Anaxagoras
Anaxagoras
Anaxagoras was a Pre-Socratic Greek philosopher. Born in Clazomenae in Asia Minor, Anaxagoras was the first philosopher to bring philosophy from Ionia to Athens. He attempted to give a scientific account of eclipses, meteors, rainbows, and the sun, which he described as a fiery mass larger than...
, who worked on it while in prison. Hippocrates of Chios
Hippocrates of Chios
Hippocrates of Chios was an ancient Greek mathematician, , and astronomer, who lived c. 470 – c. 410 BCE.He was born on the isle of Chios, where he originally was a merchant. After some misadventures he went to Athens, possibly for litigation...
squared certain lunes
Lune (mathematics)
In geometry, a lune is either of two figures, both shaped roughly like a crescent Moon. The word "lune" derives from luna, the Latin word for Moon.-Plane geometry:...
, in the hope that it would lead to a solution — see Lune of Hippocrates
Lune of Hippocrates
In geometry, the lune of Hippocrates, named after Hippocrates of Chios, is a lune bounded by arcs of circles, one of which passes through the center of the other and has half the area of the other...
. Antiphon the Sophist believed that inscribing regular polygons within a circle and doubling the number of sides will eventually fill up the area of the circle, and since a polygon can be squared, it means the circle can be squared. Even then there were skeptics—Eudemus argued that magnitudes cannot be divided up without limit, so the area of the circle will never be used up. The problem was even mentioned in Aristophanes
Aristophanes
Aristophanes , son of Philippus, of the deme Cydathenaus, was a comic playwright of ancient Athens. Eleven of his forty plays survive virtually complete...
's play The Birds
The Birds (play)
The Birds is a comedy by the Ancient Greek playwright Aristophanes. It was performed in 414 BCE at the City Dionysia where it won second prize. It has been acclaimed by modern critics as a perfectly realized fantasy remarkable for its mimicry of birds and for the gaiety of its songs...
.
It is believed that Oenopides
Oenopides
Oenopides of Chios was an ancient Greek mathematician and astronomer, who lived around 450 BCE. He was born shortly after 500 BCE on the island of Chios, but mostly worked in Athens.- Astronomy :...
was the first Greek who required a plane solution (that is, using only a compass and straightedge). James Gregory
James Gregory (astronomer and mathematician)
James Gregory FRS was a Scottish mathematician and astronomer. He described an early practical design for the reflecting telescope – the Gregorian telescope – and made advances in trigonometry, discovering infinite series representations for several trigonometric functions.- Biography :The...
attempted a proof of its impossibility in Vera Circuli et Hyperbolae Quadratura (The True Squaring of the Circle and of the Hyperbola) in 1667. Although his proof was incorrect, it was the first paper to attempt to solve the problem using algebraic properties of pi. It was not until 1882 that Ferdinand von Lindemann
Ferdinand von Lindemann
Carl Louis Ferdinand von Lindemann was a German mathematician, noted for his proof, published in 1882, that π is a transcendental number, i.e., it is not a root of any polynomial with rational coefficients....
rigorously proved its impossibility.

Lewis Carroll
Charles Lutwidge Dodgson , better known by the pseudonym Lewis Carroll , was an English author, mathematician, logician, Anglican deacon and photographer. His most famous writings are Alice's Adventures in Wonderland and its sequel Through the Looking-Glass, as well as the poems "The Hunting of the...
(better known under the pseudonym, "Lewis Carroll") also expressed interest in debunking illogical circle-squaring theories. In one of his diary entries for 1855, Dodgson listed books he hoped to write including one called "Plain Facts for Circle-Squarers". In the introduction to "A New Theory of Parallels", Dodgson recounted an attempt to demonstrate logical errors to a couple of circle-squarers, stating:
"The first of these two misguided visionaries filled me with a great ambition to do a feat I have never heard of as accomplished by man, namely to convince a circle squarer of his error! The value my friend selected for Pi was 3.2: the enormous error tempted me with the idea that it could be easily demonstrated to BE an error. More than a score of letters were interchanged before I became sadly convinced that I had no chance."
Impossibility
The solution of the problem of squaring the circle by compass and straightedge demands construction of the number , and the impossibility of this undertaking follows from the fact that pi is a transcendental
, and the impossibility of this undertaking follows from the fact that pi is a transcendentalTranscendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
(non-algebraic
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
and therefore non-constructible
Constructible number
A point in the Euclidean plane is a constructible point if, given a fixed coordinate system , the point can be constructed with unruled straightedge and compass...
) number. If the problem of the quadrature of the circle is solved using only compass and straightedge, then an algebraic value of pi would be found, which is impossible. Johann Heinrich Lambert
Johann Heinrich Lambert
Johann Heinrich Lambert was a Swiss mathematician, physicist, philosopher and astronomer.Asteroid 187 Lamberta was named in his honour.-Biography:...
conjectured that pi was transcendental in 1768 in the same paper he proved its irrationality, even before the existence of transcendental numbers was proven. It was not until 1882 that Ferdinand von Lindemann
Ferdinand von Lindemann
Carl Louis Ferdinand von Lindemann was a German mathematician, noted for his proof, published in 1882, that π is a transcendental number, i.e., it is not a root of any polynomial with rational coefficients....
proved its transcendence.
The transcendence of pi implies the impossibility of exactly "circling" the square, as well as of squaring the circle.
It is possible to construct a square with an area arbitrarily close to that of a given circle. If a rational number is used as an approximation of pi, then squaring the circle becomes possible, depending on the values chosen. However, this is only an approximation and does not meet the constraints of the ancient rules for solving the problem. Several mathematicians have demonstrated workable procedures based on a variety of approximations.
Bending the rules by allowing an infinite number of compass-and-straightedge operations or by performing the operations on certain non-Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s also makes squaring the circle possible. For example, although the circle cannot be squared in Euclidean space, it can be in Gauss–Bolyai–Lobachevsky space
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. Indeed, even the preceding phrase is overoptimistic. There are no squares as such in the hyperbolic plane, although there are regular quadrilaterals, meaning quadrilaterals with all sides congruent and all angles congruent (but these angles are strictly smaller than right angles).
There exist, in the hyperbolic plane, (countably) infinitely many pairs of constructible circles and constructible regular quadrilaterals of equal area.
However, there is no method for starting with a regular quadrilateral and constructing the circle of equal area, and there is no method for starting with a circle and constructing a regular quadrilateral of equal area (even when the circle has small enough radius such that a regular quadrilateral of equal area exists).
Modern approximative constructions
Though squaring the circle is an impossible problem using only compass and straightedge, approximations to squaring the circle can be given by constructing lengths close to pi.It takes only minimal knowledge of elementary geometry to convert any given rational approximation of pi into a corresponding compass-and-straightedge construction, but constructions made in this way tend to be very long-winded in comparison to the accuracy they achieve. After the exact problem was proven unsolvable, some mathematicians applied their ingenuity to finding elegant approximations to squaring the circle, defined roughly and informally as constructions that are particularly simple among other imaginable constructions that give similar precision.
Among the modern approximate constructions was one by E. W. Hobson
E. W. Hobson
Ernest William Hobson FRS was an English mathematician, now remembered mostly for his books, some of which broke new ground in their coverage in English of topics from mathematical analysis...
in 1913 (see his book). This was a fairly accurate construction which was based on constructing the approximate value of 3.14164079..., which is accurate to 4 decimals (i.e. it differs from pi by about ).
Indian mathematician Srinivasa Ramanujan
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
in 1913, C. D. Olds in 1963, Martin Gardner
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
in 1966, and Benjamin Bold in 1982 all gave geometric constructions for
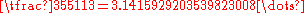
which is accurate to six decimal places of pi.

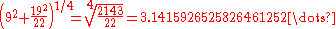
giving a remarkable eight decimal places of pi.
In 1991, Robert Dixon
Robert Dixon (mathematician)
Robert Dixon is a mathematician and graphic artist, known primarily for his book Mathographics and for his plagiarism dispute with Damien Hirst.Dixon was research associate at the Royal College of Art....
gave constructions for
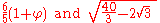
(Kochański's approximation), though these were only accurate to four decimal places of pi.
Squaring or quadrature as integration
The problem of finding the area under a curve, known as integrationIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
in calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, or quadrature in numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, was known as squaring before the invention of calculus. Since the techniques of calculus were unknown, it was generally presumed that a squaring should be done via geometric constructions, that is, by compass and straightedge. For example Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
wrote to Oldenberg in 1676 "I believe M. Leibnitz will not dislike the Theorem towards the beginning of my letter pag. 4 for squaring Curve lines Geometrically" (emphasis added). After Newton and Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
invented calculus, they still referred to this integration problem as squaring a curve.
"Squaring the circle" as a metaphor
The futility of exercises aimed at finding the quadrature of the circle has lent itself to metaphors describing a hopeless, meaningless, or vain undertaking.For example, in Spanish, the expression "descubriste la cuadratura del círculo" ("you discovered the quadrature of the circle") is often used derisively to dismiss claims that someone has found a simple solution to a particularly hard or intractable problem.
Claims of circle squaring, and the longitude problem
The mathematical proof that the quadratureNumerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
of the circle is impossible using only compass and straightedge has not proved to be a hindrance to the many people who have invested years in this problem anyway. Having squared the circle is a famous crank
Crank (person)
"Crank" is a pejorative term used for a person who unshakably holds a belief that most of his or her contemporaries consider to be false. A "cranky" belief is so wildly at variance with commonly accepted belief as to be ludicrous...
assertion. (See also pseudomathematics
Pseudomathematics
Pseudomathematics is a form of mathematics-like activity that does not work within the framework, definitions, rules, or rigor of formal mathematical models...
.) In his old age, the English philosopher Thomas Hobbes
Thomas Hobbes
Thomas Hobbes of Malmesbury , in some older texts Thomas Hobbs of Malmsbury, was an English philosopher, best known today for his work on political philosophy...
convinced himself that he had succeeded in squaring the circle.
During the 18th and 19th century the notion that the problem of squaring the circle was somehow related to the longitude problem
Longitude prize
The Longitude Prize was a reward offered by the British government for a simple and practical method for the precise determination of a ship's longitude...
seems to have become prevalent among would-be circle squarers. Using "cyclometer" for circle-squarer, Augustus de Morgan
Augustus De Morgan
Augustus De Morgan was a British mathematician and logician. He formulated De Morgan's laws and introduced the term mathematical induction, making its idea rigorous. The crater De Morgan on the Moon is named after him....
wrote in 1872:
Montucla says, speaking of France, that he finds three notions prevalent among cyclometers: 1. That there is a large reward offered for success; 2. That the longitude problem depends on that success; 3. That the solution is the great end and object of geometry. The same three notions are equally prevalent among the same class in England. No reward has ever been offered by the government of either country.
Although from 1714 to 1828 the British government did indeed sponsor a £20,000 prize
Longitude prize
The Longitude Prize was a reward offered by the British government for a simple and practical method for the precise determination of a ship's longitude...
for finding a solution to the longitude problem, exactly why the connection was made to squaring the circle is not clear; especially since two non-geometric methods (the astronomical method of lunar distances
Lunar distance (navigation)
In celestial navigation, lunar distance is the angle between the Moon and another celestial body. A navigator can use a lunar distance and a nautical almanac to calculate Greenwich time...
and the mechanical chronometer
Marine chronometer
A marine chronometer is a clock that is precise and accurate enough to be used as a portable time standard; it can therefore be used to determine longitude by means of celestial navigation...
) had been found by the late 1760s. De Morgan goes on to say that "[t]he longitude problem in no way depends upon perfect solution; existing approximations are sufficient to a point of accuracy far beyond what can be wanted." In his book, de Morgan also mentions receiving many threatening letters from would-be circle squarers, accusing him of trying to "cheat them out of their prize."
See also
- The two other classical problems of antiquity were doubling the cubeDoubling the cubeDoubling the cube is one of the three most famous geometric problems unsolvable by compass and straightedge construction...
and trisecting the angle, described in the compass and straightedgeCompass and straightedgeCompass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
article. Unlike squaring the circle, these two problems can be solved by the slightly more powerful construction method of origamiOrigamiis the traditional Japanese art of paper folding, which started in the 17th century AD at the latest and was popularized outside Japan in the mid-1900s. It has since then evolved into a modern art form...
, as described at mathematics of paper foldingMathematics of paper foldingThe art of origami or paper folding has received a considerable amount of mathematical study. Fields of interest include a given paper model's flat-foldability and the use of paper folds to solve mathematical equations.-Flat folding:The construction of origami models is sometimes shown as crease...
. - For a more modern related problem, see Tarski's circle-squaring problemTarski's circle-squaring problemTarski's circle-squaring problem is the challenge, posed by Alfred Tarski in 1925, to take a disc in the plane, cut it into finitely many pieces, and reassemble the pieces so as to get a square of equal area. This was proven to be possible by Miklós Laczkovich in 1990; the decomposition makes heavy...
. - The Indiana Pi BillIndiana Pi BillThe Indiana Pi Bill is the popular name for bill #246 of the 1897 sitting of the Indiana General Assembly, one of the most famous attempts to establish scientific truth by legislative fiat...
, an 1897 attempt by the Indiana state legislature to dictate a solution to the problem by legislative fiat. - SquircleSquircleA squircle is a mathematical shape with properties between those of a square and those of a circle. It is a special case of superellipse. The word "squircle" is a portmanteau of the words, "square" and "circle".-Equation:...
, a mathematical shape with properties between those of a square and those of a circle. - La Quadrature du NetLa Quadrature du NetLa Quadrature du Net is a French advocacy group that promotes the digital rights and freedoms of citizens. More specifically, it advocates for the adaptation of French and European legislations to respect the founding principles of the Internet, most notably the free circulation of knowledge...
, a digital-rights advocacy group.
External links
- Squaring the circle at the MacTutor History of Mathematics archiveMacTutor History of Mathematics archiveThe MacTutor History of Mathematics archive is a website maintained by John J. O'Connor and Edmund F. Robertson and hosted by the University of St Andrews in Scotland...
- Squaring the Circle at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Circle Squaring at MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
, includes information on procedures based on various approximations of pi - "Squaring the Circle" at "Convergence"
- The Quadrature of the Circle and Hippocrates' Lunes at Convergence
- How to Unroll a Circle Pi accurate to eight decimal places, using straightedge and compass.
- Squaring the Circle and Other Impossibilities, lecture by Robin WilsonRobin Wilson (mathematician)Robin James Wilson is a professor in the Department of Mathematics at the Open University, a Stipendiary Lecturer at Pembroke College, Oxford and, , Professor of Geometry at Gresham College, London, where he has also been a visiting professor...
, at Gresham CollegeGresham CollegeGresham College is an institution of higher learning located at Barnard's Inn Hall off Holborn in central London, England. It was founded in 1597 under the will of Sir Thomas Gresham and today it hosts over 140 free public lectures every year within the City of London.-History:Sir Thomas Gresham,...
, 16 January 2008 (available for download as text, audio or video file).

