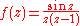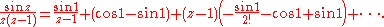Residue (complex analysis)
Encyclopedia
In mathematics
, more specifically complex analysis
, the residue is a complex number
proportional to the contour integral
of a meromorphic function
along a path enclosing one of its singularities
. (More generally, residues can be calculated for any function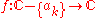 that is holomorphic except at the discrete points {ak}, even if some of them are essential singularities
that is holomorphic except at the discrete points {ak}, even if some of them are essential singularities
.) Residues can be computed quite easily and, once known, allow the determination of general contour integrals via the residue theorem
.
 at an isolated singularity
at an isolated singularity  , often denoted
, often denoted 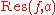 is the unique value
is the unique value  such that
such that 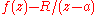 has an analytic
has an analytic
antiderivative
in a punctured disk . Alternatively, residues can be calculated by finding Laurent series
. Alternatively, residues can be calculated by finding Laurent series
expansions, and one can define the residue as the coefficient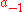 of a Laurent series
of a Laurent series
.
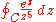
where C is some simple closed curve about 0.
Let us evaluate this integral without using standard integral theorems that may be available to us. Now, the Taylor series
for
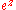
is well-known, and we substitute this series into the integrand. The integral then becomes

Let us bring the 1/z5 factor into the series, so we obtain
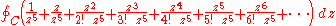

The integral now collapses to a much simpler form. Recall that

So now the integral around C of every other term not in the form cz−1 becomes zero, and the integral is reduced to
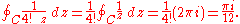
The value 1/4! is the residue of ez/z5 at z = 0, and is denoted
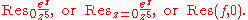
defined (at least) on D. The residue Res(f, c) of f at c is the coefficient a−1 of (z − c)−1 in the Laurent series
expansion of f around c. Various methods exist for calculating this value, and the choice of which method to use depends on the function in question, and on the nature of the singularity.
According to Cauchy's integral formula
, we have:
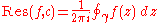
where γ traces out a circle around c in a counterclockwise manner. We may choose the path γ to be a circle of radius ε around c, where ε is as small as we desire. This may be used for calculation in cases where the integral can be calculated directly, but it is usually the case that residues are used to simplify calculation of integrals, and not the other way around.
to a holomorphic function on the whole disk { z : |z − c| < R }, then Res(f, c) = 0. The converse is not generally true.
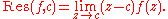
It may be that the function f can be expressed as a quotient of two functions, f(z)=g(z)/h(z), where g and h are holomorphic functions in a punctured neighbourhood of c, with h(c) = 0 and h(c) ≠ 0. In such a case, the above formula simplifies to: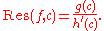
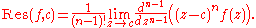
This formula can be very useful in determining the residues for low-order poles. For higher order poles, the calculations can become unmanageable, and series expansion is usually easier. Also for essential singularities
, residues often must be taken directly from series expansions.
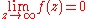
then the residue at infinity can be computed using the following formula: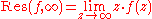
or Laurent series
, which may be possible if the parts or the whole of the function has a standard series expansion, then calculating the residue is significantly simpler than by other methods.
1. As a first example, consider calculating the residues at the singularities of the function
which may be used to calculate certain contour integrals. This function appears to have a singularity at z = 0, but if one factorizes the denominator and thus writes the function as
it is apparent that the singularity at z = 0 is a removable singularity and then the residue at z = 0 is therefore 0.
The only other singularity is at z = 1. Recall the expression for the Taylor series for a function g(z) about z = a:
So, for g(z) = sin z and a = 1 we have
and for g(z) = 1/z and a = 1 we have
Multiplying those two series and introducing 1/(z − 1) gives us
So the residue of f(z) at z = 1 is sin 1.
2. The next example shows that, computing a residue by series expansion, a major role is played by the Lagrange inversion theorem. Let
be an entire function
, and let
with positive radius of convergence, and with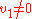 . So
. So 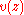 has a local inverse
has a local inverse 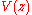 at 0, and
at 0, and 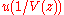 is meromorphic at 0. Then we have:
is meromorphic at 0. Then we have: .
.
Indeed,
because the first series converges uniformly on any small circle around 0. Using the Lagrange inversion theorem
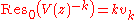 ,
,
and we get the above expression. Note that, with the corresponding stronger symmetric assumptions on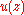 and
and 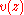 , it also follows
, it also follows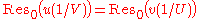 ,
,
where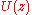 is a local inverse of
is a local inverse of  at 0.
at 0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, the residue is a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
proportional to the contour integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
of a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
along a path enclosing one of its singularities
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
. (More generally, residues can be calculated for any function
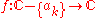 that is holomorphic except at the discrete points {ak}, even if some of them are essential singularities
that is holomorphic except at the discrete points {ak}, even if some of them are essential singularitiesEssential singularity
In complex analysis, an essential singularity of a function is a "severe" singularity near which the function exhibits extreme behavior.The category essential singularity is a "left-over" or default group of singularities that are especially unmanageable: by definition they fit into neither of the...
.) Residues can be computed quite easily and, once known, allow the determination of general contour integrals via the residue theorem
Residue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
.
Definition
The residue of a meromorphic functionMeromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
 at an isolated singularity
at an isolated singularity  , often denoted
, often denoted 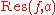 is the unique value
is the unique value  such that
such that 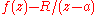 has an analytic
has an analyticAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
in a punctured disk
 . Alternatively, residues can be calculated by finding Laurent series
. Alternatively, residues can be calculated by finding Laurent seriesLaurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
expansions, and one can define the residue as the coefficient
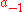 of a Laurent series
of a Laurent seriesLaurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
.
Example
As an example, consider the contour integral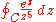
where C is some simple closed curve about 0.
Let us evaluate this integral without using standard integral theorems that may be available to us. Now, the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for
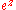
is well-known, and we substitute this series into the integrand. The integral then becomes

Let us bring the 1/z5 factor into the series, so we obtain
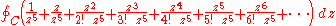

The integral now collapses to a much simpler form. Recall that

So now the integral around C of every other term not in the form cz−1 becomes zero, and the integral is reduced to
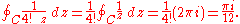
The value 1/4! is the residue of ez/z5 at z = 0, and is denoted
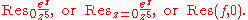
Calculating residues
Suppose a punctured disk D = {z : 0 < |z − c| < R} in the complex plane is given and f is a holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
defined (at least) on D. The residue Res(f, c) of f at c is the coefficient a−1 of (z − c)−1 in the Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
expansion of f around c. Various methods exist for calculating this value, and the choice of which method to use depends on the function in question, and on the nature of the singularity.
According to Cauchy's integral formula
Cauchy's integral formula
In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all...
, we have:
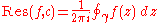
where γ traces out a circle around c in a counterclockwise manner. We may choose the path γ to be a circle of radius ε around c, where ε is as small as we desire. This may be used for calculation in cases where the integral can be calculated directly, but it is usually the case that residues are used to simplify calculation of integrals, and not the other way around.
Removable singularities
If the function f can be continuedAnalytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
to a holomorphic function on the whole disk { z : |z − c| < R }, then Res(f, c) = 0. The converse is not generally true.
Simple poles
At a simple pole c, the residue of f is given by: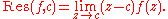
It may be that the function f can be expressed as a quotient of two functions, f(z)=g(z)/h(z), where g and h are holomorphic functions in a punctured neighbourhood of c, with h(c) = 0 and h(c) ≠ 0. In such a case, the above formula simplifies to:
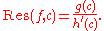
Limit formula for higher order poles
More generally, if c is a pole of order n, then the residue of f around z = c can be found by the formula: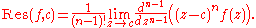
This formula can be very useful in determining the residues for low-order poles. For higher order poles, the calculations can become unmanageable, and series expansion is usually easier. Also for essential singularities
Essential singularity
In complex analysis, an essential singularity of a function is a "severe" singularity near which the function exhibits extreme behavior.The category essential singularity is a "left-over" or default group of singularities that are especially unmanageable: by definition they fit into neither of the...
, residues often must be taken directly from series expansions.
Residue at infinity
If the following condition is met: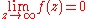
then the residue at infinity can be computed using the following formula:
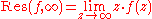
Series methods
If parts or all of a function can be expanded into a Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
or Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
, which may be possible if the parts or the whole of the function has a standard series expansion, then calculating the residue is significantly simpler than by other methods.
1. As a first example, consider calculating the residues at the singularities of the function
which may be used to calculate certain contour integrals. This function appears to have a singularity at z = 0, but if one factorizes the denominator and thus writes the function as
it is apparent that the singularity at z = 0 is a removable singularity and then the residue at z = 0 is therefore 0.
The only other singularity is at z = 1. Recall the expression for the Taylor series for a function g(z) about z = a:
So, for g(z) = sin z and a = 1 we have
and for g(z) = 1/z and a = 1 we have
Multiplying those two series and introducing 1/(z − 1) gives us
So the residue of f(z) at z = 1 is sin 1.
2. The next example shows that, computing a residue by series expansion, a major role is played by the Lagrange inversion theorem. Let

be an entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
, and let

with positive radius of convergence, and with
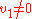 . So
. So 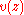 has a local inverse
has a local inverse 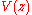 at 0, and
at 0, and 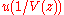 is meromorphic at 0. Then we have:
is meromorphic at 0. Then we have: .
.Indeed,

because the first series converges uniformly on any small circle around 0. Using the Lagrange inversion theorem
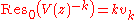 ,
,and we get the above expression. Note that, with the corresponding stronger symmetric assumptions on
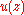 and
and 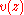 , it also follows
, it also follows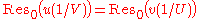 ,
,where
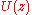 is a local inverse of
is a local inverse of  at 0.
at 0.See also
- Cauchy's integral formulaCauchy's integral formulaIn mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all...
- Cauchy integral theorem
- Methods of contour integrationMethods of contour integrationIn the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.Contour integration is closely related to the calculus of residues, a methodology of complex analysis....
- Morera's theoremMorera's theoremIn complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives an important criterion for proving that a function is holomorphic....
- Partial fractions in complex analysisPartial fractions in complex analysisIn complex analysis, a partial fraction expansion is a way of writing a meromorphic function f as an infinite sum of rational functions and polynomials...
External links
- John H. Mathews. Module for Residues.