Mikhail Vasilievich Ostrogradsky - AbsoluteAstronomy.com

Mikhail Vasilyevich Ostrogradsky (transcribed also Ostrohradskyy, Ostrogradskii, Ostrogradskiĭ) was an Russian

Russia

Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...

/ Ukrainian

Ukrainians

Ukrainians are an East Slavic ethnic group native to Ukraine, which is the sixth-largest nation in Europe. The Constitution of Ukraine applies the term 'Ukrainians' to all its citizens...

mathematician

Mathematician

A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....

, mechanician

Mechanics

Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....

and physicist

Physicist

A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...

. Ostrogradsky is considered to be a disciple of Leonhard Euler

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

and one of the leading mathematicians of Imperial Russia.

Ostrogradsky was born in Pashennaya (Пашенная), Poltava Governorate

Poltava Governorate

The Poltava Governorate or Government of Poltava was a guberniya in the historical Left-bank Ukraine region of the Russian Empire, which was officially created in 1802 from the disbanded Malorossiya Governorate which was split between the Chernigov Governorate and Poltava Governorate with an...

, Russian Empire

Russian Empire

The Russian Empire was a state that existed from 1721 until the Russian Revolution of 1917. It was the successor to the Tsardom of Russia and the predecessor of the Soviet Union...

(today Ukraine

Ukraine

Ukraine is a country in Eastern Europe. It has an area of 603,628 km², making it the second largest contiguous country on the European continent, after Russia...

). From 1816 to 1820 he studied under Timofei Fedorovich Osipovsky (1765–1832) and graduated from the University of Kharkiv

Kharkiv University

The University of Kharkiv or officially the Vasyl Karazin Kharkiv National University is one of the major universities in Ukraine, and earlier in the Russian Empire and Soviet Union...

. When 1820 Osipovsky was suspended on religious grounds, Ostrogradsky refused to be examined and he never received his Doctor's degree

Doctor of Philosophy

Doctor of Philosophy, abbreviated as Ph.D., PhD, D.Phil., or DPhil , in English-speaking countries, is a postgraduate academic degree awarded by universities...

. From 1822 to 1826 he studied at the Sorbonne

University of Paris

The University of Paris was a university located in Paris, France and one of the earliest to be established in Europe. It was founded in the mid 12th century, and officially recognized as a university probably between 1160 and 1250...

and at the Collège de France

Collège de France

The Collège de France is a higher education and research establishment located in Paris, France, in the 5th arrondissement, or Latin Quarter, across the street from the historical campus of La Sorbonne at the intersection of Rue Saint-Jacques and Rue des Écoles...

in Paris

Paris

Paris is the capital and largest city in France, situated on the river Seine, in northern France, at the heart of the Île-de-France region...

, France

France

The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...

. In 1828 he returned to the Russian Empire and settled in Saint Petersburg

Saint Petersburg

Saint Petersburg is a city and a federal subject of Russia located on the Neva River at the head of the Gulf of Finland on the Baltic Sea...

, where he was elected a member of the Academy of Sciences, Also he becomes the professor of the Main military engineering School

Military Engineering-Technical University

The Saint Petersburg Military Engineering-Technical University , previously known as the Saint Petersburg Nikolaevsky Engineering Academy, was established in 1810 under Alexander I...

of the Russian empire.

He worked mainly in the mathematical fields of calculus of variations

Calculus of variations

Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...

, integration

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

of algebraic function

Algebraic function

In mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...

s, number theory

Number theory

Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...

, algebra

Algebra

Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...

, geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

and in the fields of mathematical physics

Mathematical physics

Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...

and classical mechanics

Classical mechanics

In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...

. In the latter his most important work includes researches of the motion

Motion (physics)

In physics, motion is a change in position of an object with respect to time. Change in action is the result of an unbalanced force. Motion is typically described in terms of velocity, acceleration, displacement and time . An object's velocity cannot change unless it is acted upon by a force, as...

of an elastic body and the development of methods for integration of the equations of dynamics

Dynamics (mechanics)

In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...

. Here he continued works of Euler, Joseph Louis Lagrange

Joseph Louis Lagrange

Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...

, Siméon-Denis Poisson and Augustin Louis Cauchy

Augustin Louis Cauchy

Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...

. His work in these fields was in Russia continued by Nikolay Dmitrievich Brashman (1796–1866), August Yulevich Davidov (1823–1885) and specially by the brilliant work of Nikolai Yegorovich Zhukovsky (1847–1921).

Ostrogradsky did not appreciate the work on non-Euclidean geometry

Non-Euclidean geometry

Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...

of Nikolay Ivanovich Lobachevsky

Nikolai Ivanovich Lobachevsky

Nikolai Ivanovich Lobachevsky was a Russian mathematician and geometer, renowned primarily for his pioneering works on hyperbolic geometry, otherwise known as Lobachevskian geometry...

from 1823 and he rejected it, when it was submitted for publication in the Saint Petersburg Academy of Sciences.

His method for integrating the rational function

Rational function

In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...

s is well known. With his equation we separate integral of a fractional rational function, the sum of the rational part (algebraic fraction) and the transcendental part (with the logarithm

Logarithm

The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...

and the arctangent

Inverse trigonometric function

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions with suitably restricted domains .The notations sin−1, cos−1, etc...

). We determine the rational part without integrating it and we assign a given integral into Ostrogradsky's form:

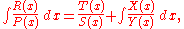
where P(x), S(x), Y(x) are known polynomials of degrees p, s and y, R(x) known polynomial of degree not greater than p − 1, T(x) and X(x) unknown polynomials of degrees not greater than s − 1 and y − 1 respectively.

Ostrogradsky died in Poltava

Poltava

Poltava is a city in located on the Vorskla River in central Ukraine. It is the administrative center of the Poltava Oblast , as well as the surrounding Poltava Raion of the oblast. Poltava's estimated population is 298,652 ....

, Poltava Governorate