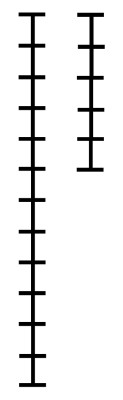
Euclidean algorithm
Encyclopedia
In mathematics
, the Euclidean algorithm (also called Euclid's algorithm) is an efficient method for computing the greatest common divisor
(GCD) of two integers, also known as the greatest common factor (GCF) or highest common factor (HCF). It is named after the Greek
mathematician
Euclid
, who described it in Books VII and X of his Elements
.
The GCD of two numbers is the largest number that divides both of them without leaving a remainder
. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the smaller number is subtracted from the larger number. For example, 21 is the GCD of 252 and 105 (252 = 21 × 12; 105 = 21 × 5); since 252 − 105 = 147, the GCD of 147 and 105 is also 21. Since the larger of the two numbers is reduced, repeating this process gives successively smaller numbers until one of them is zero. When that occurs, the GCD is the remaining nonzero number. By reversing the steps in the Euclidean algorithm
, the GCD can be expressed as a sum
of the two original numbers each multiplied by a positive or negative integer
, e.g., 21 = [5 × 105] + [(−2) × 252]. This important property is known as Bézout's identity
.
The earliest surviving description of the Euclidean algorithm is in Euclid's Elements (c. 300 BC), making it one of the oldest numerical algorithm
s still in common use. The original algorithm was described only for natural numbers and geometric lengths (real numbers), but the algorithm was generalized in the 19th century to other types of numbers, such as Gaussian integer
s and polynomial
s in one variable. This led to modern abstract algebra
ic notions such as Euclidean domain
s. The Euclidean algorithm has been generalized further to other mathematical structures, such as knots
and multivariate polynomials.
The Euclidean algorithm has many theoretical and practical applications. It may be used to generate almost all the most important traditional musical rhythms used in different cultures throughout the world. It is a key element of the RSA algorithm, a public-key encryption method widely used in electronic commerce
. It is used to solve Diophantine equations, such as finding numbers that satisfy multiple congruences (Chinese remainder theorem
) or multiplicative inverse
s of a finite field
. The Euclidean algorithm can also be used in constructing continued fraction
s, in the Sturm chain method for finding real roots of a polynomial, and in several modern integer factorization
algorithms. Finally, it is a basic tool for proving theorems in modern number theory
, such as Lagrange's four-square theorem
and the fundamental theorem of arithmetic
(unique factorization).
If implemented using remainders
of long division
rather than subtractions, Euclid's algorithm computes the GCD of large numbers efficiently: it never requires more division steps than five times the number of digits (base 10) of the smaller integer. This was proved by Gabriel Lamé
in 1844, and marks the beginning of computational complexity theory
. Methods for improving the algorithm's efficiency were developed in the 20th century.
If we reduce the larger number by subtracting the smaller one from it, the gcd does not change:

So subtract again:
Now 867 is no longer the smaller number. Continuing in the same way, we reduce the larger number, now 867, by subtracting the smaller one from it, leaving the gcd unchanged:
The first number, 255, is still the smaller one, so again we use it to reduce the larger one:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Euclidean algorithm (also called Euclid's algorithm) is an efficient method for computing the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(GCD) of two integers, also known as the greatest common factor (GCF) or highest common factor (HCF). It is named after the Greek
Greeks
The Greeks, also known as the Hellenes , are a nation and ethnic group native to Greece, Cyprus and neighboring regions. They also form a significant diaspora, with Greek communities established around the world....
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
, who described it in Books VII and X of his Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
.
The GCD of two numbers is the largest number that divides both of them without leaving a remainder
Remainder
In arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the smaller number is subtracted from the larger number. For example, 21 is the GCD of 252 and 105 (252 = 21 × 12; 105 = 21 × 5); since 252 − 105 = 147, the GCD of 147 and 105 is also 21. Since the larger of the two numbers is reduced, repeating this process gives successively smaller numbers until one of them is zero. When that occurs, the GCD is the remaining nonzero number. By reversing the steps in the Euclidean algorithm
Extended Euclidean algorithm
The extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the greatest common divisor of integers a and b, as the Euclidean algorithm does, it also finds integers x and y that satisfy Bézout's identityThe extended Euclidean algorithm is particularly useful when a...
, the GCD can be expressed as a sum
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the two original numbers each multiplied by a positive or negative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, e.g., 21 = [5 × 105] + [(−2) × 252]. This important property is known as Bézout's identity
Bézout's identity
In number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
.
The earliest surviving description of the Euclidean algorithm is in Euclid's Elements (c. 300 BC), making it one of the oldest numerical algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s still in common use. The original algorithm was described only for natural numbers and geometric lengths (real numbers), but the algorithm was generalized in the 19th century to other types of numbers, such as Gaussian integer
Gaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s and polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in one variable. This led to modern abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
ic notions such as Euclidean domain
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
s. The Euclidean algorithm has been generalized further to other mathematical structures, such as knots
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
and multivariate polynomials.
The Euclidean algorithm has many theoretical and practical applications. It may be used to generate almost all the most important traditional musical rhythms used in different cultures throughout the world. It is a key element of the RSA algorithm, a public-key encryption method widely used in electronic commerce
Electronic commerce
Electronic commerce, commonly known as e-commerce, eCommerce or e-comm, refers to the buying and selling of products or services over electronic systems such as the Internet and other computer networks. However, the term may refer to more than just buying and selling products online...
. It is used to solve Diophantine equations, such as finding numbers that satisfy multiple congruences (Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
) or multiplicative inverse
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
s of a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
. The Euclidean algorithm can also be used in constructing continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s, in the Sturm chain method for finding real roots of a polynomial, and in several modern integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
algorithms. Finally, it is a basic tool for proving theorems in modern number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, such as Lagrange's four-square theorem
Lagrange's four-square theorem
Lagrange's four-square theorem, also known as Bachet's conjecture, states that any natural number can be represented as the sum of four integer squaresp = a_0^2 + a_1^2 + a_2^2 + a_3^2\ where the four numbers are integers...
and the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
(unique factorization).
If implemented using remainders
Modulo operation
In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
of long division
Long division
In arithmetic, long division is a standard procedure suitable for dividing simple or complex multidigit numbers. It breaks down a division problem into a series of easier steps. As in all division problems, one number, called the dividend, is divided by another, called the divisor, producing a...
rather than subtractions, Euclid's algorithm computes the GCD of large numbers efficiently: it never requires more division steps than five times the number of digits (base 10) of the smaller integer. This was proved by Gabriel Lamé
Gabriel Lamé
Gabriel Léon Jean Baptiste Lamé was a French mathematician.-Biography:Lamé was born in Tours, in today's département of Indre-et-Loire....
in 1844, and marks the beginning of computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
. Methods for improving the algorithm's efficiency were developed in the 20th century.
Concrete example
Suppose it is desired to find gcd(1989, 867), i.e. the greatest common divisor of 1989 and 867.If we reduce the larger number by subtracting the smaller one from it, the gcd does not change:

So subtract again:
Now 867 is no longer the smaller number. Continuing in the same way, we reduce the larger number, now 867, by subtracting the smaller one from it, leaving the gcd unchanged:
The first number, 255, is still the smaller one, so again we use it to reduce the larger one:
-

Now 255 is the larger number and we reduce it by subtracting 102 from it:
-

Now 102 is the larger one and we reduce it by subtracting 51 from it:
Now we are done: we conclude that gcd(1989,867) = 51. Thus we must have
-

By division, we get-

When one repeatedly reduces the larger number by subtracting the smaller one from it, thus:
then the smallest number at the end, 255, is the remainderRemainderIn arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
that results from dividing 1989 by 867. Thus the algorithm is often described as follows:- Given the problem of finding gcd(1989,867), one replaces the larger number, 1989, by the remainder that results from dividing it by the smaller number, 867, getting
-
-

- Next one replaces the larger number, 867, by the remainder that results from dividing it by the now-smaller number, 255, getting
-

- Next one replaces the larger number, 255, by the remainder that results from dividing it by the now-smaller number, 102, getting
-

- Next one replaces the larger number, 102, by the remainder that results from dividing it by the now-smaller number, 51, getting
-

- When 0 appears, we are done; the gcd is 51.
-
Greatest common divisor
The Euclidean algorithm calculates the greatest common divisor (GCD) of two natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s a and b. The greatest common divisor g is the largest natural number that divides both a and b without leaving a remainder. Synonyms for the GCD include the greatest common factor (GCF), the highest common factor (HCF), and the greatest common measure (GCM). The greatest common divisor is often written as GCD(a, b) or, more simply, as (a, b), although the latter notation is also used for other mathematical concepts, such as two-dimensional vectorsCoordinate vectorIn linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
.
If GCD(a, b) = 1, then a and b are said to be coprimeCoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
(or relatively prime). This property does not imply that a or b are themselves prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. For example, neither 6 nor 35 is a prime number, since they both have two prime factors: 6 = 2 × 3 and 35 = 5 × 7. Nevertheless, 6 and 35 are coprime. No natural number other than 1 divides both 6 and 35, since they have no prime factors in common.
Let g = GCD(a, b). Since a and b are both multiples of g, they can be written a = mg and b = ng, and there is no larger number G > g for which this is true. The natural numbers m and n must be coprime, since any common factor can be factored out of m and n to make g greater. Thus, any other number c that divides both a and b must also divide g. The greatest common divisor g of a and b is the unique (positive) common divisor of a and b that is divisible by any other common divisor c.
The GCD can be visualized as follows. Consider a rectangular area a by b, and any common divisor c that divides both a and b exactly. The sides of the rectangle can be divided into segments of length c, which divides the rectangle into a grid of squares of side length c. The greatest common divisor g is the largest value of c for which this is possible. For illustration, a 24-by-60 rectangular area can be divided into a grid of: 1-by-1 squares, 2-by-2 squares, 3-by-3 squares, 4-by-4 squares, 6-by-6 squares or 12-by-12 squares. Therefore, 12 is the greatest common divisor of 24 and 60. A 24-by-60 rectangular area can be divided into a grid of 12-by-12 squares, with two squares along one edge (24/12 = 2) and five squares along the other (60/12 = 5).
The GCD of two numbers a and b is the product of the prime factors shared by the two numbers, where a same prime factor can be used multiple times, but only as long as the product of these factors divides both a and b. For example, since 1386 can be factored into 2 × 3 × 3 × 7 × 11, and 3213 can be factored into 3 × 3 × 3 × 7 × 17, the greatest common divisor of 1386 and 3213 equals 63 = 3 × 3 × 7, the product of their shared prime factors. If two numbers have no prime factors in common, their greatest common divisor is 1 (obtained here as an instance of the empty productEmpty productIn mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
), in other words they are coprime. A key advantage of the Euclidean algorithm is that it can find the GCD efficiently without having to compute the prime factors. FactorizationInteger factorizationIn number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
of large integers is believed to be a computationally very difficult problem, and the security of many modern cryptography systems is based upon its infeasibility.
Another definition of the GCD is helpful in advanced mathematics, particularly ring theoryRing theoryIn abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
. The greatest common divisor g of two nonzero numbers a and b is also their smallest positive integral linear combination, that is, the smallest positive number of the form ua + vb where u and v are integers. The set of all integral linear combinations of a and b is actually the same as the set of all multiples of g (mg, where m is an integer). In modern mathematical language, the idealIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by a and b is the ideal generated by g alone (an ideal generated by a single element is called a principal idealPrincipal idealIn ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
, and all ideals of the integers are principal ideals). Some properties of the GCD are in fact easier to see with this description, for instance the fact that any common divisor of a and b also divides the GCD (it divides both terms of ua + vb). The equivalence of this GCD definition with the other definitions is described below.
The GCD of three or more numbers equals the product of the prime factors common to all the numbers, but it can also be calculated by repeatedly taking the GCDs of pairs of numbers. For example,
- GCD(a, b, c) = GCD(a, GCD(b, c)) = GCD(GCD(a, b), c) = GCD(GCD(a, c), b).
Thus, Euclid's algorithm, which computes the GCD of two integers, suffices to calculate the GCD of arbitrarily many integers.
Induction, recursion and infinite descent
Three related mathematical methods are used in the arguments below: inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, recursionRecursionRecursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
and infinite descentInfinite descentIn mathematics, a proof by infinite descent is a particular kind of proof by contradiction which relies on the fact that the natural numbers are well ordered. One typical application is to show that a given equation has no solutions. Assuming a solution exists, one shows that another exists, that...
.
Induction is often used to prove a theorem for all natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s n. This approach begins by showing that, if the theorem holds for n, it also holds for n + 1. Therefore, if the theorem holds for one case (typically, n = 1), it holds for all higher cases (n = 2, 3, etc.).
A recursion is an equation relating numbers that form a seriesSeries (mathematics)A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
a1, a2, a3, etc. The n-th term in the series, an, is often expressed in terms of earlier terms of the series, such as an−1. For example, the Fibonacci numberFibonacci numberIn mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s are defined recursively; each term is the sum of the two preceding terms: Fn = Fn−1 + Fn−2. Several equations associated with the Euclidean algorithm are recursive.
Finally, in infinite descent, a given solution in natural numbers is used to construct a solution with smaller natural numbers. However, the solutions cannot shrink indefinitely, since there are only a finite number of natural numbers below the initial natural numbers. Therefore, either the original solution was impossible, or the construction of smaller solutions must end. The latter argument is used to show that the Euclidean algorithm for natural numbers must end in a finite number of steps.
Procedure
The Euclidean algorithm is iterative, meaning that the answer is found in a series of steps; the output of each step is used as an input for the next step. Let k be an integer that counts the steps of the algorithm, starting with zero. Thus, the initial step corresponds to k = 0, the next step corresponds to k = 1, and so on.
Each step begins with two nonnegative remainders rk−1 and rk−2. Since the algorithm ensures that the remainders decrease steadily with every step, rk−1 is less than its predecessor rk−2. The goal of the kth step is to find a quotientQuotientIn mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
qk and remainderRemainderIn arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
rk such that the equation is satisfied
- rk−2 = qk rk−1 + rk
where rk < rk−1. In other words, multiples of the smaller number rk−1 are subtracted from the larger number rk−2 until the remainder is smaller than the rk−1.
In the initial step (k = 0), the remainders r−2 and r−1 equal a and b, the numbers for which the GCD is sought. In the next step (k = 1), the remainders equal b and the remainder r0 of the initial step, and so on. Thus, the algorithm can be written as a sequence of equations
- a = q0 b + r0
- b = q1 r0 + r1
- r0 = q2 r1 + r2
- r1 = q3 r2 + r3
- …
If a is smaller than b, the first step of the algorithm swaps the numbers. For example, if a < b, the initial quotient q0 equals zero, and the remainder r0 is a. Thus, rk is smaller than its predecessor rk−1 for all k ≥ 0.
Since the remainders decrease with every step but can never be negative, a remainder rN must eventually equal zero, at which point the algorithm stops. The final nonzero remainder rN−1 is the greatest common divisor of a and b. The number N cannot be infinite because there are only a finite number of nonnegative integers between the initial remainder r0 and zero.
Proof of validity
The validity of the Euclidean algorithm can be proven by a two-step argument. In the first step, the final nonzero remainder rN−1 is shown to divide both a and b. Since it is a common divisor, it must be less than or equal to the greatest common divisor g. In the second step, it is shown that any common divisor of a and b, including g, must divide rN−1; therefore, g must be less than or equal to rN−1. These two conclusions are inconsistent unless rN−1 = g.
To demonstrate that rN−1 divides both a and b (the first step), rN−1 divides its predecessor rN−2
- rN−2 = qN rN−1
since the final remainder rN is zero. rN−1 also divides its next predecessor rN−3
- rN−3 = qN−1 rN−2 + rN−1
because it divides both terms on the right-hand side of the equation. Iterating the same argument, rN−1 divides all the preceding remainders, including a and b. None of the preceding remainders rN−2, rN−3, etc. divide a and b, since they leave a remainder. Since rN−1 is a common divisor of a and b, rN−1 ≤ g.
In the second step, any natural number c that divides both a and b (in other words, any common divisor of a and b) divides the remainders rk. By definition, a and b can be written as multiples of c: a = mc and b = nc, where m and n are natural numbers. Therefore, c divides the initial remainder r0, since r0 = a − q0b = mc − q0nc = (m − q0n)c. An analogous argument shows that c also divides the subsequent remainders r1, r2, etc. Therefore, the greatest common divisor g must divide rN−1, which implies that g ≤ rN−1. Since the first part of the argument showed the reverse (rN−1 ≤ g), it follows that g = rN−1. Thus, g is the greatest common divisor of all the succeeding pairs:
- g = GCD(a, b) = GCD(b, r0) = GCD(r0, r1) = … = GCD(rN−2, rN−1) = rN−1.
Worked example
For illustration, the Euclidean algorithm can be used to find the greatest common divisor of a = 1071 and b = 462. To begin, multiples of 462 are subtracted from 1071 until the remainder is less than 462. Two such multiples can be subtracted (q0 = 2), leaving a remainder of 147
- 1071 = 2 × 462 + 147.
Then multiples of 147 are subtracted from 462 until the remainder is less than 147. Three multiples can be subtracted (q1 = 3), leaving a remainder of 21
- 462 = 3 × 147 + 21.
Then multiples of 21 are subtracted from 147 until the remainder is less than 21. Seven multiples can be subtracted (q2 = 7), leaving no remainder
- 147 = 7 × 21 + 0.
Since the last remainder is zero, the algorithm ends with 21 as the greatest common divisor of 1071 and 462. This agrees with the GCD(1071, 462) found by prime factorization above. In tabular form, the steps are
Step k Equation Quotient and remainder 0 1071 = q0 462 + r0 q0 = 2 and r0 = 147 1 462 = q1 147 + r1 q1 = 3 and r1 = 21 2 147 = q2 21 + r2 q2 = 7 and r2 = 0; algorithm ends
Visualization
The Euclidean algorithm can be visualized in terms of the tiling analogy given above for the greatest common divisor. Assume that we wish to cover an a-by-b rectangle with square tiles exactly, where a is the larger of the two numbers. We first attempt to tile the rectangle using b-by-b square tiles; however, this leaves an r0-by-b residual rectangle untiled, where r0<b. We then attempt to tile the residual rectangle with r0-by-r0 square tiles. This leaves a second residual rectangle r1-by-r0, which we attempt to tile using r1-by-r1 square tiles, and so on. The sequence ends when there is no residual rectangle, i.e., when the square tiles cover the previous residual rectangle exactly. The length of the sides of the smallest square tile is the GCD of the dimensions of the original rectangle. For example, the smallest square tile in the adjacent figure is 21-by-21 (shown in red), and 21 is the GCD of 1071 and 462, the dimensions of the original rectangle (shown in green).
Calculating the quotients and remainders
At every step k, the Euclidean algorithm computes a quotient qk and remainder rk from two numbers rk−1 and rk−2
- rk−2 = qk rk−1 + rk
where the magnitudeAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of rk is strictly less than that of rk−1. The division algorithmDivision algorithmIn mathematics, and more particularly in arithmetic, the usual process of division of integers producing a quotient and a remainder can be specified precisely by a theorem stating that these exist uniquely with given properties. An integer division algorithm is any effective method for producing...
ensures that such a quotient and remainder always exist. The division algorithm for natural numbers also states that qk and rk are unique, but that is not needed for the Euclidean algorithm.
In Euclid's original version of the algorithm, the quotient and remainder are found by repeated subtraction; that is, rk−1 is subtracted from rk−2 repeatedly until the remainder rk is smaller than rk−1. A more efficient approach uses integer division and the modulo operationModulo operationIn computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
to calculate the quotient and remainder, respectively. The modulo operation gives the remainder after dividing two numbers; thus,
- rk ≡Modular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
rk−2 mod rk−1
The remainder is equivalent to the congruence class in modular arithmeticModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
.
Implementations
Implementations of the algorithm may be expressed in pseudocodePseudocodeIn computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
. For example, the division-based version may be programmedComputer programmingComputer programming is the process of designing, writing, testing, debugging, and maintaining the source code of computer programs. This source code is written in one or more programming languages. The purpose of programming is to create a program that performs specific operations or exhibits a...
as
function gcd(a, b)
while b ≠ 0
t := b
b := a mod b
a := t
return a
At the beginning of the kth iteration, the variable b holds the latest remainder rk−1, whereas the variable a holds its predecessor, rk−2. The step b := a mod b is equivalent to the above recursion formula rk ≡ rk−2 mod rk−1. The dummy variable t holds the value of rk−1 while the next remainder rk is being calculated. At the end of the loop iteration, the variable b holds the remainder rk, whereas the variable a holds its predecessor, rk−1.
In the subtraction-based version defined by Euclid, the remainder calculation (b = a mod b) is replaced by repeated subtraction.
function gcd(a, b)
if a = 0
return b
while b ≠ 0
if a > b
a := a − b
else
b := b − a
return a
The variables a and b alternate holding the previous remainders rk−1 and rk−2. Assume that a is larger than b at the beginning of an iteration; then a equals rk−2, since rk−2 > rk−1. During the loop iteration, a is reduced by multiples of the previous remainder b until a is smaller than b. Then a is the next remainder rk. Then b is reduced by multiples of a until it is again smaller than a, giving the next remainder rk+1, and so on.
The recursive version is based on the equality of the GCDs of successive remainders and the stopping condition GCD(rN−1, 0) = rN−1.
function gcd(a, b)
if b = 0
return a
else
return gcd(b, a mod b)
For illustration, the GCD(1071, 462) is calculated from the equivalent GCD(462, 1071 mod 462) = GCD(462, 147). The latter GCD is calculated from the GCD(147, 462 mod 147) = GCD(147, 21), which in turn is calculated from the GCD(21, 147 mod 21) = GCD(21, 0) = 21.
Method of least absolute remainders
In another version of Euclid's algorithm, the quotient at each step is increased by one if the resulting negative remainder is smaller in magnitude than the typical positive remainder. Previously, the equation
- rk−2 = qk rk−1 + rk
assumed that rk−1 > rk > 0. However, an alternative negative remainder ek can be computed
- rk−2 = (qk + 1) rk−1 + ek
where rk−1 is assumed to be positive. If |ek| < |rk|, then rk is replaced by ek. As shown by Leopold KroneckerLeopold KroneckerLeopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
, this version requires the fewest number of steps of any version of Euclid's algorithm.
Historical development
The Euclidean algorithm is one of the oldest algorithms still in common use. It appears in Euclid's Elements Euclid's ElementsEuclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
Euclid's ElementsEuclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
(c. 300 BC300 BCYear 300 BC was a year of the pre-Julian Roman calendar. At the time it was known as the Year of the Consulship of Corvus and Pansa...
), specifically in Book 7 (Propositions 1–2) and Book 10 (Propositions 2–3). In Book 7, the algorithm is formulated for integers, whereas in Book 10, it is formulated for lengths of line segments. (In modern usage, one would say it was formulated there for real numbers. But lengths, areas, and volumes, represented as real numbers in modern usage, are not measured in the same units and there is no natural unit of length, area, or volume, and the concept of real numbers was unknown at that time.) The latter algorithm is geometrical. The GCD of two lengths a and b corresponds to the greatest length g that measures a and b evenly; in other words, the lengths a and b are both integer multiples of the length g.
The algorithm was probably not discovered by EuclidEuclidEuclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
, who compiled results from earlier mathematicians in his Elements. The mathematician and historian B. L. van der WaerdenBartel Leendert van der WaerdenBartel Leendert van der Waerden was a Dutch mathematician and historian of mathematics....
suggests that Book VII derives from a textbook on number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
written by mathematicians in the school of PythagorasPythagorasPythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
. The algorithm was probably known by Eudoxus of CnidusEudoxus of CnidusEudoxus of Cnidus was a Greek astronomer, mathematician, scholar and student of Plato. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus's poem on astronomy...
(about 375 BC). The algorithm may even pre-date Eudoxus, judging from the use of the technical term ἀνθυφαίρεσις (anthyphairesis, reciprocal subtraction) in works by Euclid and Aristotle.
Centuries later, Euclid's algorithm was discovered independently both in India and in China, primarily to solve Diophantine equations that arise in astronomy and making accurate calendars. In the late fifth century, the Indian mathematician and astronomer AryabhataAryabhataAryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
described the algorithm as the "pulverizer", perhaps because of its effectiveness in solving Diophantine equations. Although a special case of the Chinese remainder theoremChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
had already been described by Chinese mathematician and astronomer Sun TzuSun Tzu (mathematician)Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
, the general solution was published by Qin Jiushao in his 1247 book Shushu Jiuzhang (數書九章 Mathematical Treatise in Nine SectionsMathematical Treatise in Nine SectionsThe Mathematical Treatise in Nine Sections is a mathematical text written by Chinese Southern Song dynasty mathematician Qin Jiushao in the year 1247.This book contains nine chapters:#Da Yan type ;#Heaven phenomena...
). The Euclidean algorithm was first described in Europe in the second edition of Bachet'sClaude Gaspard Bachet de MéziriacClaude Gaspard Bachet de Méziriac was a French mathematician, linguist, poet and classics scholar born in Bourg-en-Bresse.Bachet was a pupil of the Jesuit mathematician Jacques de Billy at the Jesuit College in Rheims...
Problèmes plaisants et délectables (Pleasant and enjoyable problems, 1624). In Europe, it was likewise used to solve Diophantine equations and in developing continued fractionContinued fractionIn mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s. The extended Euclidean algorithmExtended Euclidean algorithmThe extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the greatest common divisor of integers a and b, as the Euclidean algorithm does, it also finds integers x and y that satisfy Bézout's identityThe extended Euclidean algorithm is particularly useful when a...
was published by the English mathematician Nicholas SaundersonNicholas SaundersonNicholas Saunderson was an English scientist and mathematician. According to one leading historian of statistics, he may have been the earliest discoverer of Bayes theorem.-Biography:...
, who attributed it to Roger CotesRoger CotesRoger Cotes FRS was an English mathematician, known for working closely with Isaac Newton by proofreading the second edition of his famous book, the Principia, before publication. He also invented the quadrature formulas known as Newton–Cotes formulas and first introduced what is known today as...
as a method for computing continued fractions efficiently.
In the 19th century, the Euclidean algorithm led to the development of new number systems, such as Gaussian integerGaussian integerIn number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s and Eisenstein integerEisenstein integerIn mathematics, Eisenstein integers , also known as Eulerian integers , are complex numbers of the formz = a + b\omega \,\!where a and b are integers and...
s. In 1815, Carl GaussCarl Friedrich GaussJohann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
used the Euclidean algorithm to demonstrate unique factorization of Gaussian integerGaussian integerIn number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s, although his work was first published in 1832. Gauss mentioned the algorithm in his Disquisitiones ArithmeticaeDisquisitiones ArithmeticaeThe Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
(published 1801), but only as a method for continued fractionContinued fractionIn mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s. Peter DirichletJohann Peter Gustav Lejeune DirichletJohann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
seems to have been the first to describe the Euclidean algorithm as the basis for much of number theory. Dirichlet noted that many results of number theory, such as unique factorization, would hold true for any other system of numbers to which the Euclidean algorithm could be applied. Dirichlet's lectures on number theory were edited and extended by Richard DedekindRichard DedekindJulius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
, who used Euclid's algorithm to study algebraic integerAlgebraic integerIn number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
s, a new general type of number. For example, Dedekind was the first to prove Fermat's two-square theorem using the unique factorization of Gaussian integers. Dedekind also defined the concept of a Euclidean domainEuclidean domainIn mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
, a number system in which a generalized version of the Euclidean algorithm can be defined (as described below). In the closing decades of the 19th century, however, the Euclidean algorithm gradually became eclipsed by Dedekind's more general theory of idealsIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
.
"[The Euclidean algorithm] is the granddaddy of all algorithms, because it is the oldest nontrivial algorithm that has survived to the present day."Donald Knuth Donald KnuthDonald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
, The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 2nd edition (1981), p. 318.
Other applications of Euclid's algorithm were developed in the 19th century. In 1829, Charles Sturm showed that the algorithm was useful in the Sturm chainSturm's theoremIn mathematics, Sturm's theorem is a symbolic procedure to determine the number of distinct real roots of a polynomial. It was named for Jacques Charles François Sturm...
method for counting the real roots of polynomials in any given interval.
The Euclidean algorithm was the first integer relation algorithmInteger relation algorithmAn integer relation between a set of real numbers x1, x2, ..., xn is a set of integers a1, a2, ..., an, not all 0, such thata_1x_1 + a_2x_2 + \cdots + a_nx_n = 0.\,...
, which is a method for finding integer relations between commensurate real numbers. Several novel integer relation algorithms have been developed in recent years, such as the Ferguson–Forcade algorithm (1979) of Helaman FergusonHelaman FergusonHelaman Rolfe Pratt Ferguson is an American sculptor and a digital artist, specifically an algorist.Ferguson's mother died when he was about three and his father went off to serve in the Second World War. He was adopted and raised in New York. He was a graduate of Hamilton College and received a...
and R.W. Forcade, and its relatives, the LLL algorithmLenstra–Lenstra–Lovász lattice basis reduction algorithmThe LLL-reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik Lenstra and László Lovász in 1982, see...
, the HJLS algorithm, and the PSLQ algorithm.
In 1969, Cole and Davie developed a two-player game based on the Euclidean algorithm, called The Game of Euclid, which has an optimal strategy. The players begin with two piles of a and b stones. The players take turns removing m multiples of the smaller pile from the larger. Thus, if the two piles consist of x and y stones, where x is larger than y, the next player can reduce the larger pile from x stones to x − my stones, as long as the latter is a nonnegative integer. The winner is the first player to reduce one pile to zero stones.
Bézout's identity
Bézout's identityBézout's identityIn number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
states that the greatest common divisor g of two integers a and b can be represented as a linear sum of the original two numbers a and b. In other words, it is always possible to find integers s and t such that g = sa + tb.
The integers s and t can be calculated from the quotients q0, q1, etc. by reversing the order of equations in Euclid's algorithm. Beginning with the next-to-last equation, g can be expressed in terms of the quotient qN−1 and the two preceding remainders, rN−2 and rN−3.
- g = rN−1 = rN−3 − qN−1 rN−2
Those two remainders can be likewise expressed in terms of their quotients and preceding remainders,
- rN−2 = rN−4 − qN−2 rN−3
- rN−3 = rN−5 − qN−3 rN−4.
Substituting these formulae for rN−2 and rN−3 into the first equation yields g as a linear sum of the remainders rN−4 and rN−5. The process of substituting remainders by formulae involving their predecessors can be continued until the original numbers a and b are reached
- r2 = r0 − q2 r1
- r1 = b − q1 r0
- r0 = a − q0 b.
After all the remainders r0, r1, etc. have been substituted, the final equation expresses g as a linear sum of a and b: g = sa + tb. Bézout's identityBézout's identityIn number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
, and therefore the previous algorithm, can both be generalized to the context of Euclidean domainEuclidean domainIn mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
s.
Principal ideals and related problems
Bézout's identity provides yet another definition of the greatest common divisor g of two numbers a and b. Consider the set of all numbers ua + vb, where u and v are any two integers. Since a and b are both divisible by g, every number in the set is divisible by g. In other words, every number of the set is an integer multiple of g. This is true for every common divisor of a and b. However, unlike other common divisors, the greatest common divisor is a member of the set; by Bézout's identity, choosing u = s and v = t gives g. A smaller common divisor cannot be a member of the set, since every member of the set must be divisible by g. Conversely, any multiple m of g can be obtained by choosing u = ms and v = mt, where s and t are the integers of Bézout's identity. This may be seen by multiplying Bézout's identity by m,
- mg = msa + mtb.
Therefore, the set of all numbers ua + vb is equivalent to the set of multiples m of g. In other words, the set of all possible sums of integer multiples of two numbers (a and b) is equivalent to the set of multiples of GCD(a, b). The GCD is said to be the generator of the idealIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of a and b. This GCD definition led to the modern abstract algebraAbstract algebraAbstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
ic concepts of a principal idealPrincipal idealIn ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
(an ideal generated by a single element) and a principal ideal domainPrincipal ideal domainIn abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
(a domainDomain (ring theory)In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
in which every ideal is a principal ideal).
Certain problems can be solved using this result. For example, consider two measuring cups of volume a and b. By adding/subtracting u multiples of the first cup and v multiples of the second cup, any volume ua + vb can be measured out. These volumes are all multiples of g = GCD(a, b).
Extended Euclidean algorithm
The integers s and t of Bézout's identity can be computed efficiently using the extended Euclidean algorithmExtended Euclidean algorithmThe extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the greatest common divisor of integers a and b, as the Euclidean algorithm does, it also finds integers x and y that satisfy Bézout's identityThe extended Euclidean algorithm is particularly useful when a...
. This extension adds two recursive equations to Euclid's algorithm
- sk = sk−2 − qk−1sk−1
- tk = tk−2 − qk−1tk−1
with the starting values
- s−2 = 1, t−2 = 0
- s−1 = 0, t−1 = 1.
Using this recursion, Bézout's integers s and t are given by s = sN and t = tN, where N is the step on which the algorithm terminates with rN = 0.
The validity of this approach can be shown by induction. Assume that the recursion formula is correct up to step k−1 of the algorithm; in other words, assume that
- rj = sj a + tj b
for all j less than k. The kth step of the algorithm gives the equation
- rk = rk−2 − qk−1rk−1.
Since the recursion formula has been assumed to be correct for rk−2 and rk−1, they may be expressed in terms of the corresponding s and t variables
- rk = (sk−2 a + tk−2 b) − qk−1(sk−1 a + tk−1 b).
Rearranging this equation yields the recursion formula for step k, as required
- rk = sk a + tk b = (sk−2 − qk−1sk−1) a + (tk−2 − qk−1tk−1) b.
Matrix method
The integers s and t can also be found using an equivalent matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
method. The sequence of equations of Euclid's algorithm
- a = q0 b + r0
- b = q1 r0 + r1
- …
- rN−2 = qN rN−1 + 0
can be written as a product of 2-by-2 quotient matrices multiplying a two-dimensional remainder vector
\begin{pmatrix} a \\ b \end{pmatrix} =
\begin{pmatrix} q_0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} b \\ r_{0} \end{pmatrix} =
\begin{pmatrix} q_0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} q_1 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} r_0 \\ r_1 \end{pmatrix} =
\cdots =
\prod_{i=0}^N \begin{pmatrix} q_i & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} r_{N-1} \\ 0 \end{pmatrix}
Let M represent the product of all the quotient matrices
\mathbf{M} = \begin{pmatrix} m_{11} & m_{12} \\ m_{21} & m_{22} \end{pmatrix} =
\prod_{i=0}^N \begin{pmatrix} q_i & 1 \\ 1 & 0 \end{pmatrix} =
\begin{pmatrix} q_0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} q_1 & 1 \\ 1 & 0 \end{pmatrix} \cdots \begin{pmatrix} q_{N} & 1 \\ 1 & 0 \end{pmatrix}
This simplifies the Euclidean algorithm to the form
\begin{pmatrix} a \\ b \end{pmatrix} =
\mathbf{M} \begin{pmatrix} r_{N-1} \\ 0 \end{pmatrix} =
\mathbf{M} \begin{pmatrix} g \\ 0 \end{pmatrix}
To express g as a linear sum of a and b, both sides of this equation can be multiplied by the inverse of the matrix M. The determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of M equals (−1)N+1, since it equals the product of the determinants of the quotient matrices, each of which is negative one. Since the determinant of M is never zero, the vector of the final remainders can be solved using the inverse of M
\begin{pmatrix} g \\ 0 \end{pmatrix} =
\mathbf{M}^{-1} \begin{pmatrix} a \\ b \end{pmatrix} =
(-1)^{N+1} \begin{pmatrix} m_{22} & -m_{12} \\ -m_{21} & m_{11} \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix}
Since the top equation gives
- g = (−1)N+1 ( m22 a − m12 b)
the two integers of Bézout's identity are s = (−1)N+1m22 and t = (−1)Nm12. The matrix method is as efficient as the equivalent recursion, with two multiplications and two additions per step of the Euclidean algorithm.
Euclid's lemma and unique factorization
Bézout's identity is essential to many applications of Euclid's algorithm, such as demonstrating the unique factorization of numbers into prime factors. To illustrate this, suppose that a number L can be written as a product of two factors u and v, that is, L = uv. If another number w also divides L but is coprime with u, then w must divide v, by the following argument: If the greatest common divisor of u and w is 1, then integers s and t can be found such that
- 1 = su + tw
by Bézout's identity. Multiplying both sides by v gives the relation
- v = suv + twv = sL + twv
Since w divides both terms on the right-hand side, it must also divide the left-hand side, v. This result is known as Euclid's lemmaEuclid's lemmaIn mathematics, Euclid's lemma is an important lemma regarding divisibility and prime numbers. In its simplest form, the lemma states that a prime number that divides a product of two integers must divide one of the two integers...
. Specifically, if a prime number divides L, then it must divide at least one factor of L. Conversely, if a number w is coprime to each of a series of numbers a1, a2, …, an, then w is also coprime to their product, a1 × a2 × … × an.
Euclid's lemma suffices to prove that every number has a unique factorization into prime numbers. To see this, assume the contrary, that there are two independent factorizations of L into m and n prime factors, respectively
- L = p1p2…pm = q1q2…qn
Since each prime p divides L by assumption, it must also divide one of the q factors; since each q is prime as well, it must be that p = q. Iteratively dividing by the p factors shows that each p has an equal counterpart q; the two prime factorizations are identical except for their order. The unique factorization of numbers into primes has many applications in mathematical proofs, as shown below.
Linear Diophantine equations
Diophantine equation Diophantine equationIn mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
Diophantine equationIn mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
s are equations in which the solutions are restricted to integers; they are named after the third-century Alexandrian mathematician DiophantusDiophantusDiophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
. A typical linear Diophantine equation seeks integers x and y such that
- ax + by = c
where a, b and c are given integers. This can be written as an equation for x in modular arithmeticModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
- ax ≡ c mod b.
Let g be the greatest common divisor of a and b. Both terms in ax + by are divisible by g; therefore, c must also be divisible by g, or the equation has no solutions. By dividing both sides by c/g, the equation can be reduced to Bezout's identity
- sa + tb = g
where s and t can be found by the extended Euclidean algorithm. This provides one solution to the Diophantine equation, x1 = s (c/g) and y1 = t (c/g).
In general, a linear Diophantine equation has no solutions, or an infinite number of solutions. To find the latter, consider two solutions, (x1, y1) and (x2, y2)
- ax1 + by1 = c = ax2 + by2
or equivalently
- a(x1 − x2) = b(y2 − y1).
Therefore, the smallest difference between two x solutions is b/g, whereas the smallest difference between two y solutions is a/g. Thus, the solutions may be expressed as
- x = x1 − bt/g
- y = y1 + at/g.
By allowing t to vary over all possible integers, an infinite family of solutions can be generated from a single solution (x1, y1). If the solutions are required to be positive integers (x > 0, y > 0), only a finite number of solutions may be possible. This restriction on the acceptable solutions allows systems of Diophantine equations to be solved with more unknowns than equations; this is impossible for a system of linear equations when the solutions can be any real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
.
Multiplicative inverses and the RSA algorithm
A finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
is a set of numbers with four generalized operations. The operations are called addition, subtraction, multiplication and division and have their usual properties, such as commutativityCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
, associativityAssociativityIn mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
and distributivityDistributivityIn mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
. An example of a finite field is the set of 13 numbers {0, 1, 2, …, 12} using modular arithmeticModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
. In this field, the results of any mathematical operation (addition/subtraction/multiplication/division) is reduced moduloModulo operationIn computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
13; that is, multiples of 13 are added or subtracted until the result is brought within the range 0–12. For example, the result of 5 × 7 = 35 mod 13 = 9. Such finite fields can be defined for any prime p; using more sophisticated definitions, they can also be defined for any power m of a prime p m. Finite fields are often called GaloisÉvariste GaloisÉvariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
fields, and are abbreviated as GF(p) or GF(p m).
In such a field with m numbers, every nonzero element a has a unique modular multiplicative inverseMultiplicative inverseIn mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
, a−1 such that aa−1 = a−1a ≡ 1 mod m. This inverse can be found by solving the congruence equation ax ≡ 1 mod m, or the equivalent linear Diophantine equation
- ax + my = 1
This equation can be solved by the Euclidean algorithm, as described above. Finding multiplicative inverses is an essential step in the RSA algorithm, which is widely used in electronic commerceElectronic commerceElectronic commerce, commonly known as e-commerce, eCommerce or e-comm, refers to the buying and selling of products or services over electronic systems such as the Internet and other computer networks. However, the term may refer to more than just buying and selling products online...
; specifically, the equation determines the integer used to decrypt the message. Note that although the RSA algorithm uses ringsRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
rather than fields, the Euclidean algorithm can still be used to find a multiplicative inverse where one exists. The Euclidean algorithm also has other applications in error-correcting codes; for example, it can be used as an alternative to the Berlekamp–Massey algorithm for decoding BCHBCH codeIn coding theory the BCH codes form a class of parameterised error-correcting codes which have been the subject of much academic attention in the last fifty years. BCH codes were invented in 1959 by Hocquenghem, and independently in 1960 by Bose and Ray-Chaudhuri...
and Reed–Solomon codes, which are based on Galois fields.
Chinese remainder theorem
Euclid's algorithm can also be used to solve multiple linear Diophantine equations. Such equations arise in the Chinese remainder theoremChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
, which describes a novel method to represent an integer x. Instead of representing an integer by its digits, it may be represented by its remainders xi modulo a set of N coprime numbers mi.
- x1 ≡ x mod m1
- x2 ≡ x mod m2
- …
- xN ≡ x mod mN
The goal is to determine x from its N remainders xi. The solution is to combine the multiple equations into a single linear Diophantine equation with a much larger modulus M that is the product of all the individual moduli mi, and define the Mi
- Mi = M / mi
Thus, each Mi is the product of all the moduli except mi. The solution depends on finding N new numbers hi such that
- Mihi ≡ 1 mod mi
With these numbers hi, any integer x can be reconstructed from its remainders xi by the equation
- x ≡ (x1M1h1 + x2M2h2 + … + xNMNhN ) mod M
Since these numbers hi are the multiplicative inverses of the Mi, they may be found using Euclid's algorithm as described in the previous subsection.
Stern–Brocot Tree
The sequence of subtractions used by the Euclidean Algorithm gives a path from the root of the Stern–Brocot tree to any given rational number. This fact can be used to prove that there is a 1-1 correspondence between the vertices of tree and the positive rational numbers.
For example, 3/4 can be found by starting at the root, going to the left once, then to the right twice.
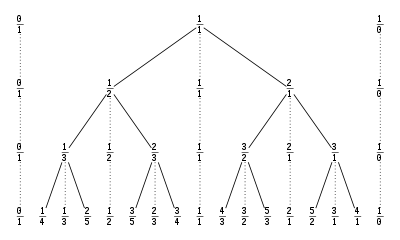

The Euclidean algorithm has almost the same relationship to the Calkin–Wilf treeCalkin–Wilf treeIn number theory, the Calkin–Wilf tree is a tree in which the vertices correspond 1-for-1 to the positive rational numbers. The tree is rooted at the number 1, and any rational number expressed in simplest terms as the fraction a/b has as its two children the numbers a/ and /b...
. The difference is that the path is reversed: instead of producing a path from the root of the tree to a target, it produces a path from the target to the root.
Continued fractions
The Euclidean algorithm has a close relationship with continued fractionContinued fractionIn mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s. The sequence of equations can be written in the form

The last term on the right-hand side always equals the inverse of the left-hand side of the next equation. Thus, the first two equations may be combined to form

The third equation may be used to substitute the denominator term r1/r0, yielding

The final ratio of remainders rk/rk−1 can always be replaced using the next equation in the series, up to the final equation. The result is a continued fraction

In the worked example above, the GCD(1071, 462) was calculated, and the quotients qk were 2, 3 and 7, respectively. Therefore, the fraction 1071/462 may be written

as can be confirmed by calculation.
Factorization algorithms
Calculating a greatest common divisor is an essential step in several integer factorizationInteger factorizationIn number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
algorithms, such as Pollard's rho algorithmPollard's rho algorithmPollard's rho algorithm is a special-purpose integer factorization algorithm. It was invented by John Pollard in 1975. It is particularly effective at splitting composite numbers with small factors.-Core ideas:...
, Shor's algorithmShor's algorithmShor's algorithm, named after mathematician Peter Shor, is a quantum algorithm for integer factorization formulated in 1994...
, Dixon's factorization methodDixon's factorization methodIn number theory, Dixon's factorization method is a general-purpose integer factorization algorithm; it is the prototypical factor base method, and the only factor base method for which a run-time bound not reliant on conjectures about the smoothness properties of values of a polynomial is...
and the Lenstra elliptic curve factorizationLenstra elliptic curve factorizationThe Lenstra elliptic curve factorization or the elliptic curve factorization method is a fast, sub-exponential running time algorithm for integer factorization which employs elliptic curves. For general purpose factoring, ECM is the third-fastest known factoring method...
. The Euclidean algorithm may be used to find this GCD efficiently. Continued fraction factorizationContinued fraction factorizationIn number theory, the continued fraction factorization method is an integer factorization algorithm. It is a general-purpose algorithm, meaning that it is suitable for factoring any integer n, not depending on special form or properties. It was described by D. H. Lehmer and R. E. Powers in 1931,...
uses continued fractions, which are determined using Euclid's algorithm.
Algorithmic efficiency
The computational efficiency of Euclid's algorithm has been studied thoroughly. This efficiency can be described by the number of steps the algorithm requires, multiplied by the computational expense of each step. As shown first by Gabriel Lamé Gabriel LaméGabriel Léon Jean Baptiste Lamé was a French mathematician.-Biography:Lamé was born in Tours, in today's département of Indre-et-Loire....
Gabriel LaméGabriel Léon Jean Baptiste Lamé was a French mathematician.-Biography:Lamé was born in Tours, in today's département of Indre-et-Loire....
in 1844, the number of steps required for completion is never more than five times the number h of digits (base 10) of the smaller number b. Since the computational expense of each step is also typically of order h, the overall expense grows like h2.
Number of steps
The number of steps to calculate the GCD of two natural numbers, a and b, may be denoted by T(a, b). If g is the GCD of a and b, then a = mg and b = ng for two coprime numbers m and n. Then
- T(a, b) = T(m, n)
as may be seen by dividing all the steps in the Euclidean algorithm by g. By the same argument, the number of steps remains the same if a and b are multiplied by a common factor w: T(a, b) = T(wa, wb). Therefore, the number of steps T may vary dramatically between neighboring pairs of numbers, such as T(a, b) and T(a, b + 1), depending on the size of the two GCDs.
The recursive nature of the Euclidean algorithm gives another equation
- T(a, b) = 1 + T(b, r0) = 2 + T(r0, r1) = … = N + T(rN−2, rN−1) = N + 1
where T(x, 0) = 0 by assumption.
Worst-case number of steps
If the Euclidean algorithm requires N steps for a pair of natural numbers a > b > 0, the smallest values of a and b for which this is true are the Fibonacci numbers FN+2 and FN+1, respectively. This can be shown by inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. If N = 1, b divides a with no remainder; the smallest natural numbers for which this is true is b = 1 and a = 2, which are F2 and F3, respectively. Now assume that the result holds for all values of N up to M − 1. The first step of the M-step algorithm is a = q0b + r0, and the second step is b = q1r0 + r1. Since the algorithm is recursive, it required M − 1 steps to find GCD(b, r0) and their smallest values are FM+1 and FM. The smallest value of a is therefore when q0 = 1, which gives a = b + r0 = FM+1 + FM = FM+2. This proof, published by Gabriel Lamé in 1844, represents the beginning of computational complexity theoryComputational complexity theoryComputational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, and also the first practical application of the Fibonacci numbers.
This result suffices to show that the number of steps in Euclid's algorithm can never be more than five times the number of its digits (base 10). For if the algorithm requires N steps, then b is greater than or equal to FN+1 which in turn is greater than or equal to φN−1, where φ is the golden ratioGolden ratioIn mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
. Since b ≥ φN−1, then N − 1 ≤ logφb. Since log10φ > 1/5, (N − 1)/5 < log10φ logφb = log10b. Thus, N ≤ 5 log10b. Thus, the Euclidean algorithm always needs less than O(h)Big O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
divisions, where h is the number of digits in the smaller number b.
Average number of steps
The average number of steps taken by the Euclidean algorithm has been defined in three different ways. The first definition is the average time T(a) required to calculate the GCD of a given number a and a smaller natural number b chosen with equal probability from the integers 0 to a − 1
T(a) = \frac{1}{a} \sum_{0 \leq b
However, since T(a, b) fluctuates dramatically with the GCD of the two numbers, the averaged function T(a) is likewise "noisy".
To reduce this noise, a second average τ(a) is taken over all numbers coprime with a
\tau(a) = \frac{1}{\varphi(a)} \sum_{0 \leq b
There are φ(a) coprime integers less than a, where φ is Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
. This tau average grows smoothly with a
- τ(a) = (12/π2) ln 2 ln a + C + O(a−(1/6) + ε)Big O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
with the residual error being of order a−(1/6) + ε, where ε is infinitesimalInfinitesimalInfinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
. The constant C in this formula equals
- C = −(1/2) + 6 (ln 2/π2)( 4γ − 24π2ζ '(2) + 3 ln 2 − 2) ≈ 1.467
where γ is the Euler–Mascheroni constantEuler–Mascheroni constantThe Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
and ζ' is the derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the Riemann zeta function. The leading coefficient (12/π2) ln 2 was determined by two independent methods.
Since the first average can be calculated from the tau average by summing over the divisors d of a
T(a) = \frac{1}{a} \sum_{d | a} \varphi(d) \tau(d)
it can be approximated by the formula
- T(a) ≈ C + (12/π2) ln 2 ( ln a − Σd|a Λ(d)/d )
where Λ(d) is the Mangoldt functionVon Mangoldt functionIn mathematics, the von Mangoldt function is an arithmetic function named after German mathematician Hans von Mangoldt.-Definition:The von Mangoldt function, conventionally written as Λ, is defined as...
.
A third average Y(n) is defined as the mean number of steps required when both a and b are chosen randomly (with uniform distribution) from 1 to n
Y(n) = \frac{1}{n^{2}} \sum_{a=1}^n \sum_{b=1}^n T(a, b) = \frac{1}{n} \sum_{a=1}^n T(a).
Substituting the approximate formula for T(a) into this equation yields an estimate for Y(n)
- Y(n) ≈ (12/π2) ln 2 ln n + 0.06.
Computational expense per step
In each step k of the Euclidean algorithm, the quotient qk and remainder rk are computed for a given pair of integers rk−2 and rk−1
- rk−2 = qk rk−1 + rk.
The computational expense per step is associated chiefly with finding qk, since the remainder rk can be calculated quickly from rk−2, rk−1, and qk
- rk = rk−2 − qk rk−1.
The computational expense of dividing h-bit numbers scales as O(h(ℓ+1)), where ℓ is the length of the quotient.
For comparison, Euclid's original subtraction-based algorithm can be much slower. A single integer division is equivalent to the quotient q number of subtractions. If the ratio of a and b is very large, the quotient is large and many subtractions will be required. On the other hand, it has been shown that the quotients are very likely to be small integers. The probability of a given quotient q is approximately ln|u/(u − 1)| where u = (q + 1)2. For illustration, the probability of a quotient of 1, 2, 3, or 4 is roughly 41.5%, 17.0%, 9.3%, and 5.9%, respectively. Since the operation of subtraction is faster than division, particularly for large numbers, the subtraction-based Euclid's algorithm is competitive with the division-based version. This is exploited in the binary versionBinary GCD algorithmThe binary GCD algorithm, also known as Stein's algorithm, is an algorithm that computes the greatest common divisor of two nonnegative integers. It gains a measure of efficiency over the ancient Euclidean algorithm by replacing divisions and multiplications with shifts, which are cheaper when...
of Euclid's algorithm.
Combining the estimated number of steps with the estimated computational expense per step shows that the Euclid's algorithm grows quadratically (h2) with the average number of digits h in the initial two numbers a and b. Let h0, h1, …, hN−1 represent the number of digits in the successive remainders r0, r1, …, rN−1. Since the number of steps N grows linearly with h, the running time is bounded by
O\Big(\sum_{i
Efficiency of alternative methods
Euclid's algorithm is widely used in practice, especially for small numbers, due to its simplicity. For comparison, the efficiency of alternatives to Euclid's algorithm may be determined.
One inefficient approach to finding the GCD of two natural numbers a and b is to calculate all their common divisors; the GCD is then the largest common divisor. The common divisors can be found by dividing both numbers by successive integers from 2 to the smaller number b. The number of steps of this approach grows linearly with b, or exponentially in the number of digits. Another inefficient approach is to find the prime factors of one or both numbers. As noted above, the GCD equals the product of the prime factors shared by the two numbers a and b. Present methods for prime factorizationInteger factorizationIn number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
are also inefficient; many modern cryptography systems even rely on that inefficiency.
The binary GCD algorithmBinary GCD algorithmThe binary GCD algorithm, also known as Stein's algorithm, is an algorithm that computes the greatest common divisor of two nonnegative integers. It gains a measure of efficiency over the ancient Euclidean algorithm by replacing divisions and multiplications with shifts, which are cheaper when...
is an efficient alternative that substitutes division with faster operations by exploiting the binaryBinary numeral systemThe binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
representation used by computers. However, this alternative also scales like O(h²). It is generally faster than the Euclidean algorithm on real computers, even though it scales in the same way. Additional efficiency can be gleaned by examining only the leading digits of the two numbers a and b. The binary algorithm can be extended to other bases (k-ary algorithms), with up to fivefold increases in speed.
A recursive approach for very large integers (with more than 25,000 digits) leads to subquadratic integer GCD algorithms, such as those of Schönhage, and Stehlé and Zimmermann. These algorithms exploit the 2×2 matrix form of the Euclidean algorithm given above. These subquadratic methods generally scale as
Other number systems
As described above, the Euclidean algorithm is used to find the greatest common divisor of two natural numbers (positive integers). However, it may be generalized to the real numbers, and to more exotic number systems such as polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, quadratic integerQuadratic integerIn number theory, quadratic integers are a generalization of the rational integers to quadratic fields. Important examples include the Gaussian integers and the Eisenstein integers. Though they have been studied for more than a hundred years, many open problems remain.- Definition :Quadratic...
s and Hurwitz quaternionHurwitz quaternionIn mathematics, a Hurwitz quaternion is a quaternion whose components are either all integers or all half-integers...
s. In the latter cases, the Euclidean algorithm is used to demonstrate the crucial property of unique factorization, i.e., that such numbers can be factored uniquely into irreducible elementIrreducible elementIn abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
s, the counterparts of prime numbers. Unique factorization is essential to many proofs of number theory.
Rational and real numbers
Euclid's algorithm can be applied to real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, as described by Euclid in Book 10 of his ElementsEuclid's ElementsEuclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
. The goal of the algorithm is to identify a real number g such that two given real numbers, a and b, are integer multiples of it: a = mg and b = ng, where m and n are integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. This identification is equivalent to finding an integer relationInteger relation algorithmAn integer relation between a set of real numbers x1, x2, ..., xn is a set of integers a1, a2, ..., an, not all 0, such thata_1x_1 + a_2x_2 + \cdots + a_nx_n = 0.\,...
among the real numbers a and b; that is, it determines integers s and t such that sa + tb = 0. Euclid uses this algorithm to treat the question of incommensurable lengthsCommensurability (mathematics)In mathematics, two non-zero real numbers a and b are said to be commensurable if a/b is a rational number.-History of the concept:...
.
The real-number Euclidean algorithm differs from its integer counterpart in two respects. First, the remainders rk are real numbers, although the quotients qk are integers as before. Second, the algorithm is not guaranteed to end in a finite number N of steps. If it does, the fraction a/b is a rational number, i.e., the ratio of two integers
- a/b = mg/ng = m/n
and can be written as a finite continued fraction [q0; q1, q2, …, qN]. If the algorithm does not stop, the fraction a/b is an irrational numberIrrational numberIn mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
and can be described by an infinite continued fraction [q0; q1, q2, …]. Examples of infinite continued fractions are the golden ratioGolden ratioIn mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
φ = [1; 1, 1, …] and the square root of twoSquare root of 2The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
, √2 = [1; 2, 2, …]. Generally speaking, the algorithm is unlikely to stop, since almost allAlmost allIn mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
ratios a/b of two real numbers are irrational.
An infinite continued fraction may be truncated at a step k [q0; q1, q2, …, qk] to yield an approximation to a/b that improves as k is increased. The approximation is described by convergentsConvergent (continued fraction)A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
mk/nk; the numerator and denominators are coprime and obey the recursion
- mk = qk mk−1 + mk−2
- nk = qk nk−1 + nk−2
where m−1 = n−2 = 1 and m−2 = n−1 = 0 are the initial values of the recursion. The convergent mk/nk is the best rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
approximation to a/b with denominator nk:
\left|\frac{a}{b} - \frac{m_k}{n_k}\right| < \frac{1}{n_k^2}.
Polynomials
Polynomials in a single variable x can be added, multiplied and factored into irreducible polynomialIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
s, which are the analogs of the prime numbers for integers. The greatest common divisor polynomial g(x) of two polynomials a(x) and b(x) is defined as the product of their shared irreducible polynomials, which can be identified using the Euclidean algorithm. The basic procedure is similar to integers. At each step k, a quotient polynomial qk(x) and a remainder polynomial rk(x) are identified to satisfy the recursive equation
- rk−2(x) = qk(x) rk−1(x) + rk(x)
where r−2(x) = a(x) and r−1(x) = b(x). The quotient polynomial is chosen so that the leading term of qk(x) rk−1(x) equals the leading term of rk−2(x); this ensures that the degree of each remainder is smaller than the degree of its predecessor deg[rk(x)] < deg[rk−1(x)]. Since the degree is a nonnegative integer, and since it decreases with every step, the Euclidean algorithm concludes in a finite number of steps. The final nonzero remainder is the greatest common divisor of the original two polynomials, a(x) and b(x).
For example, consider the following two quartic polynomials, which each factor into two quadratic polynomials
- a(x) = x4 − 4x3 + 4 x2 − 3x + 14 = (x2 − 5x + 7)(x2 + x + 2)
and
- b(x) = x4 + 8x3 + 12x2 + 17x + 6 = (x2 + 7x + 3)(x2 + x + 2).
DividingPolynomial long divisionIn algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division...
a(x) by b(x) yields a remainder r0(x) = x3 + (2/3) x2 + (5/3) x − (2/3). In the next step, b(x) is divided by r0(x) yielding a remainder r1(x) = x2 + x + 2. Finally, dividing r0(x) by r1(x) yields a zero remainder, indicating that r1(x) is the greatest common divisor polynomial of a(x) and b(x), consistent with their factorization.
Many of the applications described above for integers carry over to polynomials. The Euclidean algorithm can be used to solve linear Diophantine equations and Chinese remainder problems for polynomials; continued fractions of polynomials can also be defined.
The polynomial Euclidean algorithm has other applications as well, such as Sturm chains, a method for counting the number of real roots of a polynomial within a given interval on the real axis. This has applications in several areas, such as the Routh–Hurwitz stability criterion in control theoryControl theoryControl theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
.
Finally, the coefficients of the polynomials need not be drawn from integers, real numbers or even the complex numbers. For example, the coefficients may be drawn from a general field, such as the finite fields GF(p) described above. The corresponding conclusions about the Euclidean algorithm and its applications hold even for such polynomials.
Gaussian integers
The Gaussian integers are complex number Complex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Complex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s of the form α = u + vi, where u and v are ordinary integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s and i is the square root of negative oneImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
. By defining an analog of the Euclidean algorithm, Gaussian integers can be shown to be uniquely factorizable, by the argument above. This unique factorization is helpful in many applications, such as deriving all Pythagorean triplePythagorean tripleA Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
s or proving Fermat's theorem on sums of two squares. In general, the Euclidean algorithm is convenient in such applications, but not essential; for example, the theorems can often be proven by other arguments.
The Euclidean algorithm developed for two Gaussian integers α and β is nearly the same as that for normal integers, but differs in two respects. As before, the task at each step k is to identify a quotient qk and a remainder rk such that
- rk = rk−2 − qk rk−1
where rk−2 = α, rk−1 = β, and every remainder is strictly smaller than its predecessor, |rk| < |rk−1|. The first difference is that the quotients and remainders are themselves Gaussian integers, and thus are complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. The quotients qk are generally found by rounding the real and complex parts of the exact ratio (such as the complex number α/β) to the nearest integers. The second difference lies in the necessity of defining how one complex remainder can be "smaller" than another. To do this, we define a norm functionNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
f(u + vi) = u2 + v2, which converts every Gaussian integer u + vi into a normal integer. After each step k of the Euclidean algorithm, the norm of the remainder f(rk) is smaller than the norm of the preceding remainder, f(rk−1). Since the norm is a nonnegative integer and decreases with every step, the Euclidean algorithm for Gaussian integers ends in a finite number of steps. The final nonzero remainder is the GCD(α,β), the Gaussian integer of largest norm that divides both α and β; it is unique up to multiplication by a unit, ±1 or ±i.
Many of the other applications of the Euclidean algorithm carry over to Gaussian integers. For example, it can be used to solve linear Diophantine equations and Chinese remainder problems for Gaussian integers; continued fractions of Gaussian integers can also be defined.
Euclidean domains
A set of elements under two binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s, + and ·, is called a Euclidean domainEuclidean domainIn mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
if it forms a commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R and, roughly speaking, if a generalized Euclidean algorithm can be performed on them. The two operations of such a ring need not be the addition and multiplication of ordinary arithmetic; rather, they can be more general, such as the operations of a mathematical groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
or monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
. Nevertheless, these general operations should respect many of the laws governing ordinary arithmetic, such as commutativityCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
, associativityAssociativityIn mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
and distributivityDistributivityIn mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
.
The generalized Euclidean algorithm requires a Euclidean function, i.e., a mapping f from R into the set of nonnegative integers such that, for any two nonzero elements a and b in R, there exist q and r in R such that a = qb + r and f(r) < f(b). An example of this mapping is the norm function used to order the Gaussian integers above. The function f can be the magnitude of the number, or the degree of a polynomialDegree of a polynomialThe degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
. The basic principle is that each step of the algorithm reduces f inexorably; hence, if f can be reduced only a finite number of times, the algorithm must stop in a finite number of steps. This principle relies heavily on the natural well-ordering of the non-negative integers; roughly speaking, this requires that every set of non-negative integers has a smallest member.
The fundamental theorem of arithmeticFundamental theorem of arithmeticIn number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
applies to any Euclidean domain: Any number from a Euclidean domain can be factored uniquely into irreducible elementIrreducible elementIn abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
s. Any Euclidean domain is a unique factorization domainUnique factorization domainIn mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
(UFD), although the converse is not true. The Euclidean domains are a subclass of the GCD domainGCD domainIn mathematics, a GCD domain is an integral domain R with the property that any two non-zero elements have a greatest common divisor . Equivalently, any two non-zero elements of R have a least common multiple ....
s, domains in which a greatest common divisor of two numbers always exists. In other words, a greatest common divisor may exist (for all elements in a domain), although it may not be possible to find it using a Euclidean algorithm. A Euclidean domain is always a principal ideal domainPrincipal ideal domainIn abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
(PID), an integral domain in which every idealIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
is a principal idealPrincipal idealIn ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
. Again, the converse is not true: not every PID is a Euclidean domain.
The unique factorization of Euclidean domains is useful in many applications. For example, the unique factorization of the Gaussian integers is convenient in deriving formulae for all Pythagorean triplePythagorean tripleA Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
s and in proving Fermat's theorem on sums of two squares. Unique factorization was also a key element in an attempted proof of Fermat's Last TheoremFermat's Last TheoremIn number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
published in 1847 by Gabriel Lamé, the same mathematician who analyzed the efficiency of Euclid's algorithm, based on a suggestion of Joseph LiouvilleJoseph Liouville- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
. Lamé's approach required the unique factorization of numbers of the form x + ωy, where x and y are integers, and ω = e2iπ/n is an nth root of 1, that is, ωn = 1. Although this approach succeeds for some values of n (such as n=3, the Eisenstein integerEisenstein integerIn mathematics, Eisenstein integers , also known as Eulerian integers , are complex numbers of the formz = a + b\omega \,\!where a and b are integers and...
s), in general such numbers do not factor uniquely. This failure of unique factorization in some cyclotomic fieldCyclotomic fieldIn number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
s led Ernst KummerErnst KummerErnst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
to the concept of ideal numberIdeal numberIn number theory an ideal number is an algebraic integer which represents an ideal in the ring of integers of a number field; the idea was developed by Ernst Kummer, and led to Richard Dedekind's definition of ideals for rings...
s and, later, Richard DedekindRichard DedekindJulius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
to idealsIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
.
Unique factorization of quadratic integers
The quadratic integer rings are helpful to illustrate Euclidean domains. Quadratic integers are generalizations of the Gaussian integers in which the imaginary unit Imaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
Imaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
i is replaced by a number ω. Thus, they have the form u + v ω, where u and v are integers and ω has one of two forms, depending on a parameter D. If D does not equal a multiple of four plus one, then
- ω = √D.
If, however, D does equal a multiple of four plus one, then
- ω = (1 + √D)/2.
If the function f corresponds to a normField normIn mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
function, such as that used to order the Gaussian integers above, then the domain is known as norm-Euclidean. The norm-Euclidean rings of quadratic integers are exactly those where D = −11, −7, −3, −2, −1, 2, 3, 5, 6, 7, 11, 13, 17, 19, 21, 29, 33, 37, 41, 57 or 73. The quadratic integers with D = −1 and −3 are known as the Gaussian integerGaussian integerIn number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s and Eisenstein integerEisenstein integerIn mathematics, Eisenstein integers , also known as Eulerian integers , are complex numbers of the formz = a + b\omega \,\!where a and b are integers and...
s, respectively.
If f is allowed to be any Euclidean function, then the list of possible D values for which the domain is Euclidean is not yet known. The first example of a Euclidean domain that was not norm-Euclidean (with D = 69) was published in 1994. In 1973, Weinberger proved that a quadratic integer ring with D > 0 is Euclidean if, and only if, it is a principal ideal domainPrincipal ideal domainIn abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
, provided that the generalized Riemann hypothesisGeneralized Riemann hypothesisThe Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
holds.
Noncommutative rings
It is also possible to apply the Euclidean algorithm to noncommutative rings such as the set of Hurwitz quaternionHurwitz quaternionIn mathematics, a Hurwitz quaternion is a quaternion whose components are either all integers or all half-integers...
s. Let α and β represent two elements from such a ring. They have a common right divisor δ if α = ξδ and β = ηδ for some choice of ξ and η in the ring. Similarly, they have a common left divisor if α = δξ and β = δη for some choice of ξ and η in the ring. Since multiplication is not commutative, there are two versions of the Euclidean algorithm, one for right divisors and one for left divisors. Choosing the right divisors, the first step in finding the GCD(α, β) by the Euclidean algorithm can be written
- ρ0 = α − ψ0β = (ξ − ψ0η)δ
where ψ0 represents the quotient and ρ0 the remainder. This equation shows that any common right divisor of α and β is likewise a common divisor of the remainder ρ0. The analogous equation for the left divisors would be
- ρ0 = α − βψ0 = δ(ξ − ηψ0)
With either choice, the process is repeated as above until the greatest common right or left divisor is identified. As in the Euclidean domain, the "size" of the remainder ρ0 must be strictly smaller than β, and there must be only a finite number of possible sizes for ρ0, so that the algorithm is guaranteed to terminate.
Most of the results for the GCD carry over to noncommutative numbers. For example, Bézout's identityBézout's identityIn number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
states that the right GCD(α, β) can be expressed as a linear combination of α and β. In other words, there are numbers σ and τ such that
- Γright = σα + τβ
The analogous identity for the left GCD is nearly the same
- Γleft = ασ + βτ
Bézout's identity can be used to solve Diophantine equations.
Generalizations to other mathematical structures
The Euclidean algorithm has three general features that together ensure it will not continue indefinitely. First, it can be written as a sequence of recursive equations
- rk = rk−2 − qk rk−1
where each remainder is strictly smaller than its predecessor, |rk| < |rk−1|. Second, the size of each remainder has a strict lower limit, such as |rk| ≥ 0. Third, there is only a finite number of sizes smaller than a given remainder |rk|. Generalizations of Euclid's algorithm with these basic features have been applied to other mathematical structures, such as tangles and transfiniteTransfinite numberTransfinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers, yet not necessarily absolutely infinite. The term transfinite was coined by Georg Cantor, who wished to avoid some of the implications of the word infinite in connection with these...
ordinal numberOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s.
An important generalization of the Euclidean algorithm is the concept of a Gröbner basisGröbner basisIn computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating subset of an ideal I in a polynomial ring R...
in algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. As shown above, the GCD g of two integers a and b is the generator of their idealIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
. In other words, for any choice of the integers s and t, there is another integer m such that
- sa + tb = mg.
Although this remains true when s, t, m, a and b represent polynomials of a single variable, it is not true for rings of more than one variable. In that case, a finite set of generator polynomials g1, g2, etc. can be defined such that any linear combination of two multivariable polynomials a and b can be expressed as multiples of the generators
- sa + tb = Σk mkgk
where s, t and mk are multivariable polynomials. Any such multivariable polynomial f can be expressed as such a sum of generator polynomials plus a unique remainder polynomial r, sometimes called the normal form of polynomial f
- f = r + Σk qkgk
although the quotient polynomials qk may not be unique. The set of these generator polynomials is known as a Gröbner basis.
See also
- Binary GCD algorithmBinary GCD algorithmThe binary GCD algorithm, also known as Stein's algorithm, is an algorithm that computes the greatest common divisor of two nonnegative integers. It gains a measure of efficiency over the ancient Euclidean algorithm by replacing divisions and multiplications with shifts, which are cheaper when...
- Greatest common divisor of two polynomialsGreatest common divisor of two polynomialsInformally, the greatest common divisor of two polynomials p and q is the largest polynomial that divides both p and q evenly. The definition is modeled on the concept of the greatest common divisor of two integers, the greatest integer that divides both...
- Integer relation algorithmInteger relation algorithmAn integer relation between a set of real numbers x1, x2, ..., xn is a set of integers a1, a2, ..., an, not all 0, such thata_1x_1 + a_2x_2 + \cdots + a_nx_n = 0.\,...
- Lehmer's GCD algorithmLehmer's GCD algorithmLehmer's GCD algorithm, named after Derrick Henry Lehmer, is a rather fast GCD algorithm, an improvement on the simpler but slower Euclidean algorithm...
External links
- Demonstrations of Euclid's algorithm
- Euclid's Algorithm at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- The Euclidean Algorithm at MathPages
- Euclid's Game at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Music and Euclid's algorithm
-
-
-
-





