
Fundamental theorem of algebra
Encyclopedia
The fundamental theorem
of algebra states that every non-constant single-variable polynomial
with complex
coefficient
s has at least one complex root. Equivalently, the field
of complex number
s is algebraically closed
.
Sometimes, this theorem is stated as: every non-zero single-variable polynomial with complex coefficients has exactly as many complex roots as its degree, if each root is counted up to its multiplicity
. Although this at first appears to be a stronger statement, it is a direct consequence of the other form of the theorem, through the use of successive polynomial division by linear factors.
In spite of its name, there is no purely algebraic proof of the theorem, since any proof must use the completeness
of the reals (or some other equivalent formulation of completeness), which is not an algebraic concept. Additionally, it is not fundamental for modern algebra
; its name was given at a time when the study of algebra was mainly concerned with the solutions of polynomial equations with real or complex coefficients.
, in his book L'invention nouvelle en l'Algèbre (published in 1629), asserted that a polynomial equation of degree n has n solutions, but he did not state that they had to be real numbers. Furthermore, he added that his assertion holds “unless the equation is incomplete”, by which he meant that no coefficient is equal to 0. However, when he explains in detail what he means, it is clear that he actually believes that his assertion is always true; for instance, he shows that the equation x4 = 4x − 3, although incomplete, has four solutions (counting multiplicities): 1 (twice), −1 + i√2, and −1 − i√2.
As will be mentioned again below, it follows from the fundamental theorem of algebra that every non-constant polynomial with real coefficients can be written as a product of polynomials with real coefficients whose degree is either 1 or 2. However, in 1702 Leibniz
said that no polynomial of the type x4 + a4 (with a real and distinct from 0) can be written in such a way. Later, Nikolaus Bernoulli
made the same assertion concerning the polynomial x4 − 4x3 + 2x2 + 4x + 4, but he got a letter from Euler
in 1742 in which he was told that his polynomial happened to be equal to
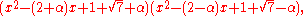
where α is the square root of 4 + 2√7. Also, Euler mentioned that

A first attempt at proving the theorem was made by d'Alembert
in 1746, but his proof was incomplete. Among other problems, it assumed implicitly a theorem (now known as Puiseux's theorem) which would not be proved until more than a century later, and furthermore the proof assumed the fundamental theorem of algebra. Other attempts were made by Euler
(1749), de Foncenex (1759), Lagrange
(1772), and Laplace
(1795). These last four attempts assumed implicitly Girard's assertion; to be more precise, the existence of solutions was assumed and all that remained to be proved was that their form was a + bi for some real numbers a and b. In modern terms, Euler, de Foncenex, Lagrange, and Laplace were assuming the existence of a splitting field
of the polynomial p(z).
At the end of the 18th century, two new proofs were published which did not assume the existence of roots. One of them, due to James Wood and mainly algebraic, was published in 1798 and it was totally ignored. Wood's proof had an algebraic gap. The other one was published by Gauss
in 1799 and it was mainly geometric, but it had a topological gap, filled by Alexander Ostrowski
in 1920, as discussed in Smale 1981 http://projecteuclid.org/DPubS?service=UI&version=1.0&verb=Display&handle=euclid.bams/1183547848 (Smale writes, "...I wish to point out what an immense gap Gauss' proof contained. It is a subtle point even today that a real algebraic plane curve cannot enter a disk without leaving. In fact even though Gauss redid this proof 50 years later, the gap remained. It was not until 1920 that Gauss' proof was completed. In the reference Gauss, A. Ostrowski has a paper which does this and gives an excellent discussion of the problem as well..."). A rigorous proof was published by Argand
in 1806; it was here that, for the first time, the fundamental theorem of algebra was stated for polynomials with complex coefficients, rather than just real coefficients. Gauss produced two other proofs in 1816 and another version of his original proof in 1849.
The first textbook containing a proof of the theorem was Cauchy's Cours d'analyse de l'École Royale Polytechnique (1821). It contained Argand's proof, although Argand is not credited for it.
None of the proofs mentioned so far is constructive
. It was Weierstrass who raised for the first time, in the middle of the 19th century, the problem of finding a constructive proof
of the fundamental theorem of algebra. He presented his solution, that amounts in modern terms to a combination of the Durand–Kerner method with the homotopy continuation principle
, in 1891. Another proof of this kind was obtained by Hellmuth Kneser
in 1940 and simplified by his son Martin Kneser
in 1981.
Without using countable choice, it is not possible to constructively prove the fundamental theorem of algebra for complex numbers based on the Dedekind real numbers (which are not constructively equivalent to the Cauchy real numbers without countable choice). However, Fred Richman proved a reformulated version of the theorem that does work.
, at the very least the concept of continuity
of real or complex functions. Some also use differentiable
or even analytic
functions. This fact has led some to remark that the Fundamental Theorem of Algebra is neither fundamental, nor a theorem of algebra.
Some proofs of the theorem only prove that any non-constant polynomial with real coefficients has some complex root. This is enough to establish the theorem in the general case because, given a non-constant polynomial p(z) with complex coefficients, the polynomial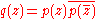
has only real coefficients and, if z is a zero of q(z), then either z or its conjugate is a root of p(z).
A large number of non-algebraic proofs of the theorem use the fact (sometimes called “growth lemma”) that an n-th degree polynomial function p(z) whose dominant coefficient is 1 behaves like zn when |z| is large enough. A more precise statement is: there is some positive real number R such that:
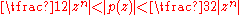
when |z| > R.
D of radius r centered at the origin such that |p(z)| > |p(0)| whenever |z| ≥ r. The minimum of |p(z)| on D, which must exist since D is compact, is therefore achieved at some point z0 in the interior of D, but not at any point of its boundary. The minimum modulus principle
implies then that p(z0) = 0. In other words, z0 is a zero of p(z).
A variation of this proof that does not require the use of the minimum modulus principle (most proofs of which in turn require the use of Cauchy's integral theorem
or some of its consequences) is based on the observation that for the special case of a polynomial function, the minimum modulus principle can be proved directly using elementary arguments. More precisely, if we assume by contradiction that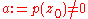 , then, expanding
, then, expanding 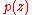 in powers of
in powers of 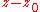 we can write
we can write
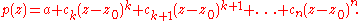
Here, the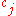 's are simply the coefficients of the polynomial
's are simply the coefficients of the polynomial 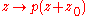 , and we let
, and we let 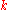 be the index of the first coefficient following the constant term that is non-zero. But now we see that for
be the index of the first coefficient following the constant term that is non-zero. But now we see that for  sufficiently close to
sufficiently close to  this has behavior asymptotically similar to the simpler polynomial
this has behavior asymptotically similar to the simpler polynomial
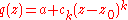 , in the sense that (as is easy to check) the function
, in the sense that (as is easy to check) the function
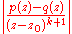
is bounded by some positive constant in some neighborhood of
in some neighborhood of  .
.
Therefore if we define and let
and let  , then for any sufficiently small positive number
, then for any sufficiently small positive number  (so that the bound
(so that the bound  mentioned above holds), using the triangle inequality we see that
mentioned above holds), using the triangle inequality we see that
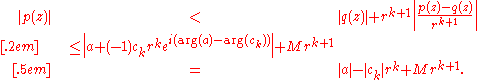
When r is sufficiently close to 0 this upper bound for |p(z)| is strictly smaller than |a|, in contradiction to the definition of z0. (Geometrically, we have found an explicit direction θ0 such that if one approaches z0 from that direction one can obtain values p(z) smaller in absolute value than |p(z0)|.)
Another analytic proof can be obtained along this line of thought observing that, since |p(z)| > |p(0)| outside D, the minimum of |p(z)| on the whole complex plane is achieved at z0. If |p(z0)| > 0, then 1/p is a bounded holomorphic function
in the entire complex plane since, for each complex number z, |1/p(z)| ≤ |1/p(z0)|. Applying Liouville's theorem
, which states that a bounded entire function must be constant, this would imply that 1/p is constant and therefore that p is constant. This gives a contradiction, and hence p(z0) = 0.
Yet another analytic proof uses the argument principle
. Let R be a positive real number large enough so that every root of p(z) has absolute value smaller than R; such a number must exist because every non-constant polynomial function of degree n has at most n zeros. For each r > R, consider the number

where c(r) is the circle centered at 0 with radius r oriented counterclockwise; then the argument principle
says that this number is the number N of zeros of p(z) in the open ball centered at 0 with radius r, which, since r > R, is the total number of zeros of p(z). On the other hand, the integral of n/z along c(r) divided by 2πi is equal to n. But the difference between the two numbers is
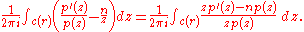
The numerator of the rational expression being integrated has degree at most n − 1 and the degree of the denominator is n + 1. Therefore, the number above tends to 0 as r tends to +∞. But the number is also equal to N − n and so N = n.
Still another complex-analytic proof can be given by combining linear algebra
with the Cauchy theorem
. To establish that every complex polynomial of degree n > 0 has a zero, it suffices to show that every complex square matrix of size n > 0 has a (complex) eigenvalue. The proof of the latter statement is by contradiction.
Let A be a complex square matrix of size n > 0 and let In be the unit matrix of the same size. Assume A has no eigenvalues. Consider the resolvent function
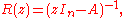
which is a meromorphic function
on the complex plane with values in the vector space of matrices. The eigenvalues of A are precisely the poles of R(z). Since, by assumption, A has no eigenvalues, the function R(z) is an entire function
and Cauchy's theorem implies that
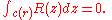
On the other hand, R(z) expanded as a geometric series gives:

This formula is valid outside the closed disc of radius ||A|| (the operator norm
of A). Let r > ||A||. Then

(in which only the summand k = 0 has a nonzero integral). This is a contradiction, and so A has an eigenvalue.
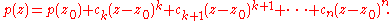
It follows that if a is a kth root of −p(z0)/ck and if t is positive and sufficiently small, then |p(z0 + ta)| < |p(z0)|, which is impossible, since |p(z0)| is the minimum of |p| on D.
For another topological proof by contradiction, suppose that p(z) has no zeros. Choose a large positive number R such that, for |z| = R, the leading term zn of p(z) dominates all other terms combined; in other words, such that |z|n > |an − 1zn −1 + ··· + a0|. As z traverses the circle given by the equation |z| = R once counter-clockwise, p(z), like zn, winds n times counter-clockwise around 0. At the other extreme, with |z| = 0, the “curve” p(z) is simply the single (nonzero) point p(0), whose winding number
is clearly 0. If the loop followed by z is continuously deformed
between these extremes, the path of p(z) also deforms continuously. We can explicitly write such a deformation as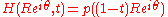 where t is greater than or equal to 0 and less than or equal to 1. If one views the variable t as time, then at time zero the curve is p(z) and at time one the curve is p(0). Clearly at every point t, p(z) cannot be zero by the original assumption, therefore during the deformation, the curve never crosses zero. Therefore the winding number of the curve around zero should never change. However, given that the winding number started as n and ended as 0, this is absurd. Therefore, p(z) has at least one zero.
where t is greater than or equal to 0 and less than or equal to 1. If one views the variable t as time, then at time zero the curve is p(z) and at time one the curve is p(0). Clearly at every point t, p(z) cannot be zero by the original assumption, therefore during the deformation, the curve never crosses zero. Therefore the winding number of the curve around zero should never change. However, given that the winding number started as n and ended as 0, this is absurd. Therefore, p(z) has at least one zero.
):
The second fact, together with the quadratic formula, implies the theorem for real quadratic polynomials. In other words, algebraic proofs of the fundamental theorem actually show that if R is any real-closed field, then its extension is algebraically closed.
is algebraically closed.
As mentioned above, it suffices to check the statement “every non-constant polynomial p(z) with real coefficients has a complex root”. This statement can be proved by induction on the greatest non-negative integer k such that 2k divides the degree n of p(z). Let a be the coefficient of zn in p(z) and let F be a splitting field
of p(z) over C; in other words, the field F contains C and there are elements z1, z2, ..., zn in F such that

If k = 0, then n is odd, and therefore p(z) has a real root. Now, suppose that n = 2km (with m odd and k > 0) and that the theorem is already proved when the degree of the polynomial has the form 2k − 1m′ with m′ odd. For a real number t, define:

Then the coefficients of qt(z) are symmetric polynomial
s in the zis with real coefficients. Therefore, they can be expressed as polynomials with real coefficients in the elementary symmetric polynomial
s, that is, in −a1, a2, ..., (−1)nan. So qt(z) has in fact real coefficients. Furthermore, the degree of qt(z) is n(n − 1)/2 = 2k − 1m(n − 1), and m(n − 1) is an odd number. So, using the induction hypothesis, qt has at least one complex root; in other words, zi + zj + tzizj is complex for two distinct elements i and j from {1,...,n}. Since there are more real numbers than pairs (i,j), one can find distinct real numbers t and s such that zi + zj + tzizj and zi + zj + szizj are complex (for the same i and j). So, both zi + zj and zizj are complex numbers. It is easy to check that every complex number has a complex square root, thus every complex polynomial of degree 2 has a complex root by the quadratic formula. It follows that zi and zj are complex numbers, since they are roots of the quadratic polynomial z2 − (zi + zj)z + zizj.
J. Shipman showed in 2007 that the assumption that odd degree polynomials have roots is stronger than necessary; any field in which polynomials of prime degree have roots is algebraically closed (so "odd" can be replaced by "odd prime" and furthermore this holds for fields of all characteristics). For axiomatization of algebraically closed fields, this is the best possible, as there are counterexamples if a single prime is excluded. However, these counterexamples rely on −1 having a square root. If we take a field where −1 has no square root, and every polynomial of degree n ∈ I has a root, where I is any fixed infinite set of odd numbers, then every polynomial f(x) of odd degree has a root (since has a root, where k is chosen so that ).
Another algebraic proof of the fundamental theorem can be given using Galois theory
. It suffices to show that C has no proper finite field extension
. Let K/C be a finite extension. Since the normal closure of K over R still has a finite degree over C (or R), we may assume without loss of generality
that K is a normal extension
of R (hence it is a Galois extension
, as every algebraic extension of a field of characteristic
0 is separable
). Let G be the Galois group
of this extension, and let H be a Sylow 2-group of G, so that the order
of H is a power of 2, and the index
of H in G is odd. By the fundamental theorem of Galois theory
, there exists a subextension L of K/R such that Gal(K/L) = H. As [L:R] = [G:H] is odd, and there are no nonlinear irreducible real polynomials of odd degree, we must have L = R, thus [K:R] and [K:C] are powers of 2. Assuming for contradiction [K:C] > 1, the 2-group
Gal(K/C) contains a subgroup of index 2, thus there exists a subextension M of C of degree 2. However, C has no extension of degree 2, because every quadratic complex polynomial has a complex root, as mentioned above.
, it follows that any theorem concerning algebraically closed fields applies to the field of complex numbers. Here are a few more consequences of the theorem, which are either about the field of real numbers or about the relationship between the field of real numbers and the field of complex numbers:
 of a monic polynomial
of a monic polynomial  satisfy an inequality
satisfy an inequality  where
where
Notice that, as stated, this is not yet an existence result but rather an example of what is called an a priori bound: it says that if there are solutions
then they lie inside the closed disk of center the origin and radius . However, once coupled with the fundamental theorem of algebra it says that the disk contains in fact at least one solution. More generally, a bound can be given directly in terms of any p-norm of the n-vector of coefficients
. However, once coupled with the fundamental theorem of algebra it says that the disk contains in fact at least one solution. More generally, a bound can be given directly in terms of any p-norm of the n-vector of coefficients  , that is
, that is  , where
, where 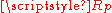 is precisely the q-norm of the 2-vector
is precisely the q-norm of the 2-vector  , q being the conjugate exponent of p, 1/p + 1/q = 1, for any
, q being the conjugate exponent of p, 1/p + 1/q = 1, for any  . Thus, the modulus of any solution is also bounded by
. Thus, the modulus of any solution is also bounded by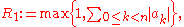
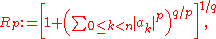
for , and in particular
, and in particular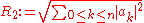
(where we define to mean 1, which is reasonable since 1 is indeed the n-th coefficient of our polynomial).
to mean 1, which is reasonable since 1 is indeed the n-th coefficient of our polynomial).
The case of a generic polynomial of degree n, , is of course reduced to the case of a monic, dividing all coefficients by
, is of course reduced to the case of a monic, dividing all coefficients by 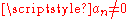 . Also, in case that 0 is not a root, i.e.
. Also, in case that 0 is not a root, i.e. 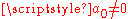 , bounds from below on the roots
, bounds from below on the roots  follow immediately as bounds from above on
follow immediately as bounds from above on  , that is, the roots of
, that is, the roots of 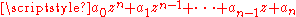 . Finally, the distance
. Finally, the distance 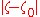 from the roots
from the roots  to any point
to any point 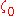 can be estimated from below and above, seeing
can be estimated from below and above, seeing 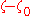 as zeroes of the polynomial
as zeroes of the polynomial  , whose coefficients are the Taylor expansion of
, whose coefficients are the Taylor expansion of 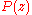 at
at 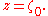
We report the here the proof of the above bounds, which is short and elementary. Let be a root of the polynomial
be a root of the polynomial  ; in order to prove the inequality
; in order to prove the inequality  we can assume, of course,
we can assume, of course, 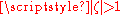 . Writing the equation as
. Writing the equation as 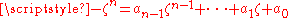 , and using the Hölder's inequality
, and using the Hölder's inequality
we find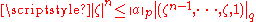 . Now, if
. Now, if  , this is
, this is  , thus
, thus 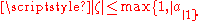 . In the case
. In the case  , taking into account the summation formula for a geometric progression
, taking into account the summation formula for a geometric progression
, we have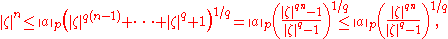
thus and simplifying,
and simplifying,  . Therefore
. Therefore
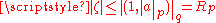 holds, for all
holds, for all 
, part 1: Algebraic Analysis). English translation: (tr. New proof of the theorem that every integral rational algebraic function of one variable can be resolved into real factors of the first or second degree).
and integral calculus.) (tr. The rational functions §80–88: the fundamental theorem). http://projecteuclid.org/DPubS?service=UI&version=1.0&verb=Display&handle=euclid.bams/1183547848
Fundamental theorem
The fundamental theorem of a field of mathematics is the theorem considered central to that field. The naming of such a theorem is not necessarily based on how often it is used or the difficulty of its proofs....
of algebra states that every non-constant single-variable polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s has at least one complex root. Equivalently, the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s is algebraically closed
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
.
Sometimes, this theorem is stated as: every non-zero single-variable polynomial with complex coefficients has exactly as many complex roots as its degree, if each root is counted up to its multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
. Although this at first appears to be a stronger statement, it is a direct consequence of the other form of the theorem, through the use of successive polynomial division by linear factors.
In spite of its name, there is no purely algebraic proof of the theorem, since any proof must use the completeness
Completeness (order theory)
In the mathematical area of order theory, completeness properties assert the existence of certain infima or suprema of a given partially ordered set . A special use of the term refers to complete partial orders or complete lattices...
of the reals (or some other equivalent formulation of completeness), which is not an algebraic concept. Additionally, it is not fundamental for modern algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
; its name was given at a time when the study of algebra was mainly concerned with the solutions of polynomial equations with real or complex coefficients.
History
Peter Rothe (Petrus Roth), in his book Arithmetica Philosophica (published in 1608), wrote that a polynomial equation of degree n (with real coefficients) may have n solutions. Albert GirardAlbert Girard
Albert Girard was a French-born mathematician. He studied at the University of Leiden. He "had early thoughts on the fundamental theorem of algebra" and gave the inductive definition for the Fibonacci numbers....
, in his book L'invention nouvelle en l'Algèbre (published in 1629), asserted that a polynomial equation of degree n has n solutions, but he did not state that they had to be real numbers. Furthermore, he added that his assertion holds “unless the equation is incomplete”, by which he meant that no coefficient is equal to 0. However, when he explains in detail what he means, it is clear that he actually believes that his assertion is always true; for instance, he shows that the equation x4 = 4x − 3, although incomplete, has four solutions (counting multiplicities): 1 (twice), −1 + i√2, and −1 − i√2.
As will be mentioned again below, it follows from the fundamental theorem of algebra that every non-constant polynomial with real coefficients can be written as a product of polynomials with real coefficients whose degree is either 1 or 2. However, in 1702 Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
said that no polynomial of the type x4 + a4 (with a real and distinct from 0) can be written in such a way. Later, Nikolaus Bernoulli
Nicolaus I Bernoulli
Nicolaus Bernoulli , was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family....
made the same assertion concerning the polynomial x4 − 4x3 + 2x2 + 4x + 4, but he got a letter from Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
in 1742 in which he was told that his polynomial happened to be equal to
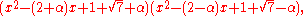
where α is the square root of 4 + 2√7. Also, Euler mentioned that

A first attempt at proving the theorem was made by d'Alembert
Jean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert was a French mathematician, mechanician, physicist, philosopher, and music theorist. He was also co-editor with Denis Diderot of the Encyclopédie...
in 1746, but his proof was incomplete. Among other problems, it assumed implicitly a theorem (now known as Puiseux's theorem) which would not be proved until more than a century later, and furthermore the proof assumed the fundamental theorem of algebra. Other attempts were made by Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
(1749), de Foncenex (1759), Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
(1772), and Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
(1795). These last four attempts assumed implicitly Girard's assertion; to be more precise, the existence of solutions was assumed and all that remained to be proved was that their form was a + bi for some real numbers a and b. In modern terms, Euler, de Foncenex, Lagrange, and Laplace were assuming the existence of a splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
of the polynomial p(z).
At the end of the 18th century, two new proofs were published which did not assume the existence of roots. One of them, due to James Wood and mainly algebraic, was published in 1798 and it was totally ignored. Wood's proof had an algebraic gap. The other one was published by Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in 1799 and it was mainly geometric, but it had a topological gap, filled by Alexander Ostrowski
Alexander Ostrowski
Alexander Markowich Ostrowski , was a mathematician.His father Mark having been a merchant, Alexander Ostrowski attended the Kiev College of Commerce, not a high school, and thus had an insufficient qualification to be admitted to university...
in 1920, as discussed in Smale 1981 http://projecteuclid.org/DPubS?service=UI&version=1.0&verb=Display&handle=euclid.bams/1183547848 (Smale writes, "...I wish to point out what an immense gap Gauss' proof contained. It is a subtle point even today that a real algebraic plane curve cannot enter a disk without leaving. In fact even though Gauss redid this proof 50 years later, the gap remained. It was not until 1920 that Gauss' proof was completed. In the reference Gauss, A. Ostrowski has a paper which does this and gives an excellent discussion of the problem as well..."). A rigorous proof was published by Argand
Jean-Robert Argand
Jean-Robert Argand was a gifted amateur mathematician. In 1806, while managing a bookstore in Paris, he published the idea of geometrical interpretation of complex numbers known as the Argand diagram.-Life:...
in 1806; it was here that, for the first time, the fundamental theorem of algebra was stated for polynomials with complex coefficients, rather than just real coefficients. Gauss produced two other proofs in 1816 and another version of his original proof in 1849.
The first textbook containing a proof of the theorem was Cauchy's Cours d'analyse de l'École Royale Polytechnique (1821). It contained Argand's proof, although Argand is not credited for it.
None of the proofs mentioned so far is constructive
Constructivism (mathematics)
In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
. It was Weierstrass who raised for the first time, in the middle of the 19th century, the problem of finding a constructive proof
Constructive proof
In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object with certain properties by creating or providing a method for creating such an object...
of the fundamental theorem of algebra. He presented his solution, that amounts in modern terms to a combination of the Durand–Kerner method with the homotopy continuation principle
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
, in 1891. Another proof of this kind was obtained by Hellmuth Kneser
Hellmuth Kneser
Hellmuth Kneser was a German mathematician, who made notable contributions to group theory and topology. His most famous result may be his theorem on the existence of a prime decomposition for 3-manifolds...
in 1940 and simplified by his son Martin Kneser
Martin Kneser
Martin Kneser was a German mathematician. His father Hellmuth Kneser and grandfather Adolf Kneser were also mathematicians....
in 1981.
Without using countable choice, it is not possible to constructively prove the fundamental theorem of algebra for complex numbers based on the Dedekind real numbers (which are not constructively equivalent to the Cauchy real numbers without countable choice). However, Fred Richman proved a reformulated version of the theorem that does work.
Proofs
All proofs below involve some analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, at the very least the concept of continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
of real or complex functions. Some also use differentiable
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
or even analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
functions. This fact has led some to remark that the Fundamental Theorem of Algebra is neither fundamental, nor a theorem of algebra.
Some proofs of the theorem only prove that any non-constant polynomial with real coefficients has some complex root. This is enough to establish the theorem in the general case because, given a non-constant polynomial p(z) with complex coefficients, the polynomial
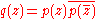
has only real coefficients and, if z is a zero of q(z), then either z or its conjugate is a root of p(z).
A large number of non-algebraic proofs of the theorem use the fact (sometimes called “growth lemma”) that an n-th degree polynomial function p(z) whose dominant coefficient is 1 behaves like zn when |z| is large enough. A more precise statement is: there is some positive real number R such that:
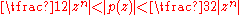
when |z| > R.
Complex-analytic proofs
Find a closed diskDisk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
D of radius r centered at the origin such that |p(z)| > |p(0)| whenever |z| ≥ r. The minimum of |p(z)| on D, which must exist since D is compact, is therefore achieved at some point z0 in the interior of D, but not at any point of its boundary. The minimum modulus principle
Maximum modulus principle
In mathematics, the maximum modulus principle in complex analysis states that if f is a holomorphic function, then the modulus |f| cannot exhibit a true local maximum that is properly within the domain of f....
implies then that p(z0) = 0. In other words, z0 is a zero of p(z).
A variation of this proof that does not require the use of the minimum modulus principle (most proofs of which in turn require the use of Cauchy's integral theorem
Cauchy's integral theorem
In mathematics, the Cauchy integral theorem in complex analysis, named after Augustin-Louis Cauchy, is an important statement about line integrals for holomorphic functions in the complex plane...
or some of its consequences) is based on the observation that for the special case of a polynomial function, the minimum modulus principle can be proved directly using elementary arguments. More precisely, if we assume by contradiction that
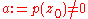 , then, expanding
, then, expanding  in powers of
in powers of  we can write
we can write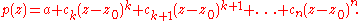
Here, the
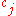 's are simply the coefficients of the polynomial
's are simply the coefficients of the polynomial 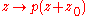 , and we let
, and we let 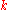 be the index of the first coefficient following the constant term that is non-zero. But now we see that for
be the index of the first coefficient following the constant term that is non-zero. But now we see that for  sufficiently close to
sufficiently close to  this has behavior asymptotically similar to the simpler polynomial
this has behavior asymptotically similar to the simpler polynomial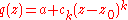 , in the sense that (as is easy to check) the function
, in the sense that (as is easy to check) the function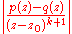
is bounded by some positive constant
 in some neighborhood of
in some neighborhood of  .
.Therefore if we define
 and let
and let  , then for any sufficiently small positive number
, then for any sufficiently small positive number  (so that the bound
(so that the bound  mentioned above holds), using the triangle inequality we see that
mentioned above holds), using the triangle inequality we see that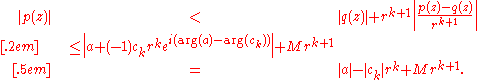
When r is sufficiently close to 0 this upper bound for |p(z)| is strictly smaller than |a|, in contradiction to the definition of z0. (Geometrically, we have found an explicit direction θ0 such that if one approaches z0 from that direction one can obtain values p(z) smaller in absolute value than |p(z0)|.)
Another analytic proof can be obtained along this line of thought observing that, since |p(z)| > |p(0)| outside D, the minimum of |p(z)| on the whole complex plane is achieved at z0. If |p(z0)| > 0, then 1/p is a bounded holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
in the entire complex plane since, for each complex number z, |1/p(z)| ≤ |1/p(z0)|. Applying Liouville's theorem
Liouville's theorem (complex analysis)
In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function f for which there exists a positive number M such that |f| ≤ M for all z in C is constant.The theorem is considerably improved by...
, which states that a bounded entire function must be constant, this would imply that 1/p is constant and therefore that p is constant. This gives a contradiction, and hence p(z0) = 0.
Yet another analytic proof uses the argument principle
Argument principle
In complex analysis, the argument principle determines the difference between the number of zeros and poles of a meromorphic function by computing a contour integral of the function's logarithmic derivative....
. Let R be a positive real number large enough so that every root of p(z) has absolute value smaller than R; such a number must exist because every non-constant polynomial function of degree n has at most n zeros. For each r > R, consider the number

where c(r) is the circle centered at 0 with radius r oriented counterclockwise; then the argument principle
Argument principle
In complex analysis, the argument principle determines the difference between the number of zeros and poles of a meromorphic function by computing a contour integral of the function's logarithmic derivative....
says that this number is the number N of zeros of p(z) in the open ball centered at 0 with radius r, which, since r > R, is the total number of zeros of p(z). On the other hand, the integral of n/z along c(r) divided by 2πi is equal to n. But the difference between the two numbers is
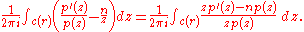
The numerator of the rational expression being integrated has degree at most n − 1 and the degree of the denominator is n + 1. Therefore, the number above tends to 0 as r tends to +∞. But the number is also equal to N − n and so N = n.
Still another complex-analytic proof can be given by combining linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
with the Cauchy theorem
Cauchy theorem
Several theorems are named after Augustin-Louis Cauchy. Cauchy theorem may mean:*Cauchy's integral theorem in complex analysis, also Cauchy's integral formula*Cauchy's mean value theorem in real analysis, an extended form of the mean value theorem...
. To establish that every complex polynomial of degree n > 0 has a zero, it suffices to show that every complex square matrix of size n > 0 has a (complex) eigenvalue. The proof of the latter statement is by contradiction.
Let A be a complex square matrix of size n > 0 and let In be the unit matrix of the same size. Assume A has no eigenvalues. Consider the resolvent function
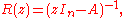
which is a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
on the complex plane with values in the vector space of matrices. The eigenvalues of A are precisely the poles of R(z). Since, by assumption, A has no eigenvalues, the function R(z) is an entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
and Cauchy's theorem implies that
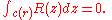
On the other hand, R(z) expanded as a geometric series gives:

This formula is valid outside the closed disc of radius ||A|| (the operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
of A). Let r > ||A||. Then

(in which only the summand k = 0 has a nonzero integral). This is a contradiction, and so A has an eigenvalue.
Topological proofs
Let z0 ∈ C be such that the minimum of |p(z)| on the whole complex plane is achieved at z0; it was seen at the proof which uses Liouville's theorem that such a number must exist. We can write p(z) as a polynomial in z − z0: there is some natural number k and there are some complex numbers ck, ck + 1, ..., cn such that ck ≠ 0 and that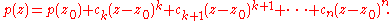
It follows that if a is a kth root of −p(z0)/ck and if t is positive and sufficiently small, then |p(z0 + ta)| < |p(z0)|, which is impossible, since |p(z0)| is the minimum of |p| on D.
For another topological proof by contradiction, suppose that p(z) has no zeros. Choose a large positive number R such that, for |z| = R, the leading term zn of p(z) dominates all other terms combined; in other words, such that |z|n > |an − 1zn −1 + ··· + a0|. As z traverses the circle given by the equation |z| = R once counter-clockwise, p(z), like zn, winds n times counter-clockwise around 0. At the other extreme, with |z| = 0, the “curve” p(z) is simply the single (nonzero) point p(0), whose winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
is clearly 0. If the loop followed by z is continuously deformed
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
between these extremes, the path of p(z) also deforms continuously. We can explicitly write such a deformation as
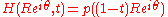 where t is greater than or equal to 0 and less than or equal to 1. If one views the variable t as time, then at time zero the curve is p(z) and at time one the curve is p(0). Clearly at every point t, p(z) cannot be zero by the original assumption, therefore during the deformation, the curve never crosses zero. Therefore the winding number of the curve around zero should never change. However, given that the winding number started as n and ended as 0, this is absurd. Therefore, p(z) has at least one zero.
where t is greater than or equal to 0 and less than or equal to 1. If one views the variable t as time, then at time zero the curve is p(z) and at time one the curve is p(0). Clearly at every point t, p(z) cannot be zero by the original assumption, therefore during the deformation, the curve never crosses zero. Therefore the winding number of the curve around zero should never change. However, given that the winding number started as n and ended as 0, this is absurd. Therefore, p(z) has at least one zero.Algebraic proofs
These proofs use two facts about real numbers that require only a small amount of analysis (more precisely, the intermediate value theoremIntermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
):
- every polynomial with odd degree and real coefficients has some real root;
- every non-negative real number has a square root.
The second fact, together with the quadratic formula, implies the theorem for real quadratic polynomials. In other words, algebraic proofs of the fundamental theorem actually show that if R is any real-closed field, then its extension
 is algebraically closed.
is algebraically closed.As mentioned above, it suffices to check the statement “every non-constant polynomial p(z) with real coefficients has a complex root”. This statement can be proved by induction on the greatest non-negative integer k such that 2k divides the degree n of p(z). Let a be the coefficient of zn in p(z) and let F be a splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
of p(z) over C; in other words, the field F contains C and there are elements z1, z2, ..., zn in F such that

If k = 0, then n is odd, and therefore p(z) has a real root. Now, suppose that n = 2km (with m odd and k > 0) and that the theorem is already proved when the degree of the polynomial has the form 2k − 1m′ with m′ odd. For a real number t, define:

Then the coefficients of qt(z) are symmetric polynomial
Symmetric polynomial
In mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
s in the zis with real coefficients. Therefore, they can be expressed as polynomials with real coefficients in the elementary symmetric polynomial
Elementary symmetric polynomial
In mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
s, that is, in −a1, a2, ..., (−1)nan. So qt(z) has in fact real coefficients. Furthermore, the degree of qt(z) is n(n − 1)/2 = 2k − 1m(n − 1), and m(n − 1) is an odd number. So, using the induction hypothesis, qt has at least one complex root; in other words, zi + zj + tzizj is complex for two distinct elements i and j from {1,...,n}. Since there are more real numbers than pairs (i,j), one can find distinct real numbers t and s such that zi + zj + tzizj and zi + zj + szizj are complex (for the same i and j). So, both zi + zj and zizj are complex numbers. It is easy to check that every complex number has a complex square root, thus every complex polynomial of degree 2 has a complex root by the quadratic formula. It follows that zi and zj are complex numbers, since they are roots of the quadratic polynomial z2 − (zi + zj)z + zizj.
J. Shipman showed in 2007 that the assumption that odd degree polynomials have roots is stronger than necessary; any field in which polynomials of prime degree have roots is algebraically closed (so "odd" can be replaced by "odd prime" and furthermore this holds for fields of all characteristics). For axiomatization of algebraically closed fields, this is the best possible, as there are counterexamples if a single prime is excluded. However, these counterexamples rely on −1 having a square root. If we take a field where −1 has no square root, and every polynomial of degree n ∈ I has a root, where I is any fixed infinite set of odd numbers, then every polynomial f(x) of odd degree has a root (since has a root, where k is chosen so that ).
Another algebraic proof of the fundamental theorem can be given using Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
. It suffices to show that C has no proper finite field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
. Let K/C be a finite extension. Since the normal closure of K over R still has a finite degree over C (or R), we may assume without loss of generality
Without loss of generality
Without loss of generality is a frequently used expression in mathematics...
that K is a normal extension
Normal extension
In abstract algebra, an algebraic field extension L/K is said to be normal if L is the splitting field of a family of polynomials in K[X]...
of R (hence it is a Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
, as every algebraic extension of a field of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
0 is separable
Separable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
). Let G be the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of this extension, and let H be a Sylow 2-group of G, so that the order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of H is a power of 2, and the index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
of H in G is odd. By the fundamental theorem of Galois theory
Fundamental theorem of Galois theory
In mathematics, the fundamental theorem of Galois theory is a result that describes the structure of certain types of field extensions.In its most basic form, the theorem asserts that given a field extension E /F which is finite and Galois, there is a one-to-one correspondence between its...
, there exists a subextension L of K/R such that Gal(K/L) = H. As [L:R] = [G:H] is odd, and there are no nonlinear irreducible real polynomials of odd degree, we must have L = R, thus [K:R] and [K:C] are powers of 2. Assuming for contradiction [K:C] > 1, the 2-group
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
Gal(K/C) contains a subgroup of index 2, thus there exists a subextension M of C of degree 2. However, C has no extension of degree 2, because every quadratic complex polynomial has a complex root, as mentioned above.
Corollaries
Since the fundamental theorem of algebra can be seen as the statement that the field of complex numbers is algebraically closedAlgebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
, it follows that any theorem concerning algebraically closed fields applies to the field of complex numbers. Here are a few more consequences of the theorem, which are either about the field of real numbers or about the relationship between the field of real numbers and the field of complex numbers:
- The field of complex numbers is the algebraic closureAlgebraic closureIn mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of the field of real numbers. - Every polynomial in one variable x with real coefficients is the product of a constant, polynomials of the form x + a with a real, and polynomials of the form x2 + ax + b with a and b real and a2 − 4b < 0 (which is the same thing as saying that the polynomial x2 + ax + b has no real roots).
- Every rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
in one variable x, with real coefficients, can be written as the sum of a polynomial function with rational functions of the form a/(x − b)n (where n is a natural number, and a and b are real numbers), and rational functions of the form (ax + b)/(x2 + cx + d)n (where n is a natural number, and a, b, c, and d are real numbers such that c2 − 4d < 0). A corollaryCorollaryA corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
of this is that every rational function in one variable and real coefficients has an elementaryElementary function (differential algebra)In mathematics, an elementary function is a function of one variable built from a finite number of exponentials, logarithms, constants, and nth roots through composition and combinations using the four elementary operations...
primitiveAntiderivativeIn calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
. - Every algebraic extensionAlgebraic extensionIn abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
of the real field is isomorphic either to the real field or to the complex field.
Bounds on the zeroes of a polynomial
While the fundamental theorem of algebra states a general existence result, it is of some interest, both from the theoretical and from the practical point of view, to have information on the location of the zeroes of a given polynomial. The simpler result in this direction is a bound on the modulus: all zeroes of a monic polynomial
of a monic polynomial  satisfy an inequality
satisfy an inequality  where
where
Notice that, as stated, this is not yet an existence result but rather an example of what is called an a priori bound: it says that if there are solutions
then they lie inside the closed disk of center the origin and radius
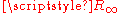 . However, once coupled with the fundamental theorem of algebra it says that the disk contains in fact at least one solution. More generally, a bound can be given directly in terms of any p-norm of the n-vector of coefficients
. However, once coupled with the fundamental theorem of algebra it says that the disk contains in fact at least one solution. More generally, a bound can be given directly in terms of any p-norm of the n-vector of coefficients 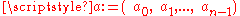 , that is
, that is  , where
, where 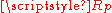 is precisely the q-norm of the 2-vector
is precisely the q-norm of the 2-vector  , q being the conjugate exponent of p, 1/p + 1/q = 1, for any
, q being the conjugate exponent of p, 1/p + 1/q = 1, for any  . Thus, the modulus of any solution is also bounded by
. Thus, the modulus of any solution is also bounded by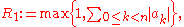
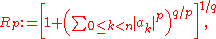
for
 , and in particular
, and in particular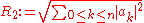
(where we define
 to mean 1, which is reasonable since 1 is indeed the n-th coefficient of our polynomial).
to mean 1, which is reasonable since 1 is indeed the n-th coefficient of our polynomial).The case of a generic polynomial of degree n,
 , is of course reduced to the case of a monic, dividing all coefficients by
, is of course reduced to the case of a monic, dividing all coefficients by 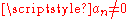 . Also, in case that 0 is not a root, i.e.
. Also, in case that 0 is not a root, i.e. 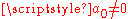 , bounds from below on the roots
, bounds from below on the roots  follow immediately as bounds from above on
follow immediately as bounds from above on  , that is, the roots of
, that is, the roots of 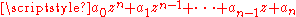 . Finally, the distance
. Finally, the distance 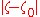 from the roots
from the roots  to any point
to any point 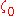 can be estimated from below and above, seeing
can be estimated from below and above, seeing 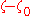 as zeroes of the polynomial
as zeroes of the polynomial  , whose coefficients are the Taylor expansion of
, whose coefficients are the Taylor expansion of 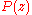 at
at 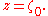
We report the here the proof of the above bounds, which is short and elementary. Let
 be a root of the polynomial
be a root of the polynomial  ; in order to prove the inequality
; in order to prove the inequality  we can assume, of course,
we can assume, of course,  . Writing the equation as
. Writing the equation as 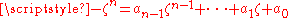 , and using the Hölder's inequality
, and using the Hölder's inequalityHölder's inequality
In mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces....
we find
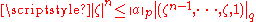 . Now, if
. Now, if  , this is
, this is  , thus
, thus 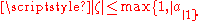 . In the case
. In the case  , taking into account the summation formula for a geometric progression
, taking into account the summation formula for a geometric progressionGeometric progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
, we have
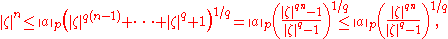
thus
 and simplifying,
and simplifying,  . Therefore
. Therefore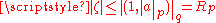 holds, for all
holds, for all 
Historic sources
(tr. Course on Analysis of the Royal Polytechnic AcademyÉcole Polytechnique
The École Polytechnique is a state-run institution of higher education and research in Palaiseau, Essonne, France, near Paris. Polytechnique is renowned for its four year undergraduate/graduate Master's program...
, part 1: Algebraic Analysis). English translation: (tr. New proof of the theorem that every integral rational algebraic function of one variable can be resolved into real factors of the first or second degree).
- C. F. Gauss, “Another new proof of the theorem that every integral rational algebraic function of one variable can be resolved into real factors of the first or second degree”, 1815 (The Fundamental Theorem of Algebra and IntuitionismIntuitionismIn the philosophy of mathematics, intuitionism, or neointuitionism , is an approach to mathematics as the constructive mental activity of humans. That is, mathematics does not consist of analytic activities wherein deep properties of existence are revealed and applied...
). (tr. An extension of a work of Hellmuth KneserHellmuth KneserHellmuth Kneser was a German mathematician, who made notable contributions to group theory and topology. His most famous result may be his theorem on the existence of a prime decomposition for 3-manifolds...
on the Fundamental Theorem of Algebra). (tr. On the first and fourth Gaussian proofs of the Fundamental Theorem of Algebra). (tr. New proof of the theorem that every integral rational function of one variable can be represented as a product of linear functions of the same variable).
Recent literature
(tr. On the history of the fundamental theorem of algebra: theory of equationsTheory of equations
In mathematics, the theory of equations comprises a major part of traditional algebra. Topics include polynomials, algebraic equations, separation of roots including Sturm's theorem, approximation of roots, and the application of matrices and determinants to the solving of equations.From the point...
and integral calculus.) (tr. The rational functions §80–88: the fundamental theorem). http://projecteuclid.org/DPubS?service=UI&version=1.0&verb=Display&handle=euclid.bams/1183547848
External links
- Fundamental Theorem of Algebra — a collection of proofs
- D. J. Velleman: The Fundamental Theorem of Algebra: A Visual Approach, PDF (unpublished paper), visualisation of d'Alembert's, Gauss's and the winding number proofs
- Fundamental Theorem of Algebra Module by John H. Mathews
- Bibliography for the Fundamental Theorem of Algebra
- From the Fundamental Theorem of Algebra to Astrophysics: A "Harmonious" Path

