
Equation
Encyclopedia
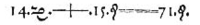
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
statement that asserts the equality of two expressions
Expression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
. In modern notation, this is written by placing the expressions on either side of an equals sign
Equals sign
The equality sign, equals sign, or "=" is a mathematical symbol used to indicate equality. It was invented in 1557 by Robert Recorde. The equals sign is placed between the things stated to have the same value, as in an equation...
(=), for example

asserts that x+3 is equal to 5. The = symbol was invented by Robert Recorde
Robert Recorde
Robert Recorde was a Welsh physician and mathematician. He introduced the "equals" sign in 1557.-Biography:A member of a respectable family of Tenby, Wales, he entered the University of Oxford about 1525, and was elected a fellow of All Souls College in 1531...
(1510–1558), who considered that nothing could be more equal than parallel straight lines with the same length.
Knowns and unknowns
Equations often express relationships between given quantities, the knowns, and quantities yet to be determined, the unknowns. By convention, unknowns are denoted by letters at the end of the alphabet, x, y, z, w, …, while knowns are denoted by letters at the beginning, a, b, c, d, … . The process of expressing the unknowns in terms of the knowns is called solving the equationEquation solving
In mathematics, to solve an equation is to find what values fulfill a condition stated in the form of an equation . These expressions contain one or more unknowns, which are free variables for which values are sought that cause the condition to be fulfilled...
. In an equation with a single unknown, a value of that unknown for which the equation is true is called a solution or root of the equation. In a set simultaneous equations
Simultaneous equations
In mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations...
, or system of equations, multiple equations are given with multiple unknowns. A solution to the system is an assignment of values to all the unknowns so that all of the equations are true.
Types of equations
Equations can be classified according to the types of operationsOperation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
and quantities involved. Important types include:
- An algebraic equation is an equation involving only algebraic expressions in the unknowns. These are further classified by degreeDegree (mathematics)In mathematics, there are several meanings of degree depending on the subject.- Unit of angle :A degree , usually denoted by ° , is a measurement of a plane angle, representing 1⁄360 of a turn...
. - A linear equationLinear equationA linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
is algebraic equation of degree one. - A polynomial equation is an equation in which a polynomial is set equal to another polynomial.
- A transcendental equation is an equation involving a transcendental function of one of its variables.
- A functional equationFunctional equationIn mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
is an equation in which the unknowns are functionsFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
rather than simple quantities. - A differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
is an equation involving derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s. - An integral equationIntegral equationIn mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
is an equation involving integralIntegralIntegration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s. - A Diophantine equationDiophantine equationIn mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
is an equation where the unknowns are required to be integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s.
Identities
One use of equations is in mathematical identitiesIdentity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
, assertions that are true independent of the values of any variables contained within them. For example, for any given value of x it is true that

However, equations can also be correct for only certain values of the variables. In this case, they can be solved
Equation solving
In mathematics, to solve an equation is to find what values fulfill a condition stated in the form of an equation . These expressions contain one or more unknowns, which are free variables for which values are sought that cause the condition to be fulfilled...
to find the values that satisfy the equality. For example, consider the following.

The equation is true only for two values of x, the solutions of the equation. In this case, the solutions are
 and
and  .
.Many mathematicians reserve the term equation exclusively for the second type, to signify an equality which is not an identity. The distinction between the two concepts can be subtle; for example,

is an identity, while

is an equation with solutions
 and
and  . Whether a statement is meant to be an identity or an equation can usually be determined from its context. In some cases, a distinction is made between the equality sign (
. Whether a statement is meant to be an identity or an equation can usually be determined from its context. In some cases, a distinction is made between the equality sign ( ) for an equation and the equivalence symbol (
) for an equation and the equivalence symbol ( ) for an identity.
) for an identity.Letters from the beginning of the alphabet like a, b, c... often denote constants
Constant (mathematics)
In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
in the context of the discussion at hand, while letters from the end of the alphabet, like ...x, y, z, are usually reserved for the variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
, a convention initiated by Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
.
Properties
If an equation in algebraElementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
is known to be true, the following operations may be used to produce another true equation:
- Any real number can be addedAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
to both sides. - Any real number can be subtractedSubtractionIn arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
from both sides. - Any real number can be multipliedMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
to both sides. - Any non-zero real number can divideDivision (mathematics)right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
both sides. - Some functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s can be applied to both sides. Caution must be exercised to ensure that the operation does not cause missing or extraneous solutions. For example, the equation y*x=x has 2 solutions: y=1 and x=0. Dividing both sides by x "simplifies" the equation to y=1, but the second solution is lost.
The algebraic properties (1-4) imply that equality is a congruence relation
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
for a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
; in fact, it is essentially the only one.
The most well known system of numbers which allows all of these operations is the real numbers, which is an example of a field. However, if the equation were based on the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s for example, some of these operations (like division and subtraction) may not be valid as negative numbers and non-whole numbers are not allowed. The integers are an example of an integral domain which does not allow all divisions as, again, whole numbers are needed. However, subtraction is allowed, and is the inverse operator in that system.
If a function that is not injective is applied to both sides of a true equation, then the resulting equation will still be true, but it may be less useful. Formally, one has an implication, not an equivalence
Logical biconditional
In logic and mathematics, the logical biconditional is the logical connective of two statements asserting "p if and only if q", where q is a hypothesis and p is a conclusion...
, so the solution set may get larger. The functions implied in properties (1), (2), and (4) are always injective, as is (3) if we do not multiply by zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
. Some generalized product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
s, such as a dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
, are never injective.
More information at Equation solving
Equation solving
In mathematics, to solve an equation is to find what values fulfill a condition stated in the form of an equation . These expressions contain one or more unknowns, which are free variables for which values are sought that cause the condition to be fulfilled...
.
External links
- Winplot: General Purpose plotter which can draw and animate 2D and 3D mathematical equations.
- Mathematical equation plotter: Plots 2D mathematical equations, computes integrals, and finds solutions online.
- Equation plotter: A web page for producing and downloading pdf or postscript plots of the solution sets to equations and inequations in two variables (x and y).
- EqWorld—contains information on solutions to many different classes of mathematical equations.
- EquationSolver: A webpage that can solve single equations and linear equation systems.

