In elementary algebra

Elementary algebra

Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...

, the binomial theorem describes the algebraic expansion of powers

Exponentiation

Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...

 of a binomial

Binomial

In algebra, a binomial is a polynomial with two terms —the sum of two monomials—often bound by parenthesis or brackets when operated upon...

. According to the theorem, it is possible to expand the power (x + y)ⁿ into a sum

SUM

SUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...

 involving terms of the form ax^by^c, where the exponents b and c are nonnegative integers with , and the coefficient

Coefficient

In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...

 a of each term is a specific positive integer depending on n and b. When an exponent is zero, the corresponding power is usually omitted from the term. For example,


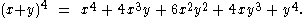
The coefficient a in the term of x^by^c is known as the binomial coefficient

Binomial coefficient

In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...

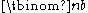  or 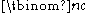(the two have the same value). These coefficients for varying n and b can be arranged to form Pascal's triangle

Pascal's triangle

In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...

. These numbers also arise in combinatorics

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

, where 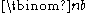gives the number of different combinations of b elements that can be chosen from an n-element set.

History

This formula and the triangular arrangement of the binomial coefficients are often attributed to Blaise Pascal

Blaise Pascal

Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...

, who described them in the 17th century, but they were known to many mathematicians who preceded him. The 4th century B.C. Greek mathematician

Greek mathematics

Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...

 Euclid

Euclid

Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...

 mentioned the special case of the binomial theorem for exponent 2 as did the 3rd century B.C. Indian mathematician

Indian mathematics

Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...

 Pingala

Pingala

Pingala is the traditional name of the author of the ' , the earliest known Sanskrit treatise on prosody.Nothing is known about Piṅgala himself...

 to higher orders. A more general binomial theorem and the so-called "Pascal's triangle

Pascal's triangle

In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...

" were known in the 10th-century A.D. to Indian mathematician Halayudha

Halayudha

Halayudha was a 10th century Indian mathematician who wrote the ', a commentary on Pingala's Chandah-shastra, containing a clear description of Pascal's triangle ....

 and Persian mathematician

Islamic mathematics

In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...

 Al-Karaji

Al-Karaji

' was a 10th century Persian Muslim mathematician and engineer. His three major works are Al-Badi' fi'l-hisab , Al-Fakhri fi'l-jabr wa'l-muqabala , and Al-Kafi fi'l-hisab .Because al-Karaji's original works in Arabic are lost, it is not...

,, in the 11th century to Persian poet and mathematician Omar Khayyam, and in the 13th century to Chinese mathematician

Chinese mathematics

Mathematics in China emerged independently by the 11th century BC. The Chinese independently developed very large and negative numbers, decimals, a place value decimal system, a binary system, algebra, geometry, and trigonometry....

 Yang Hui

Yang Hui

Yang Hui , courtesy name Qianguang , was a Chinese mathematician from Qiantang , Zhejiang province during the late Song Dynasty . Yang worked on magic squares, magic circles and the binomial theorem, and is best known for his contribution of presenting 'Yang Hui's Triangle'...

, who all derived similar results. Al-Karaji also provided a mathematical proof

Mathematical proof

In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...

 of both the binomial theorem and Pascal's triangle, using mathematical induction

Mathematical induction

Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...

.

Statement of the theorem

According to the theorem, it is possible to expand any power of x + y into a sum of the form


where each is a specific positive integer known as binomial coefficient

Binomial coefficient

In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...

. This formula is also referred to as the Binomial Formula or the Binomial Identity. Using summation notation, it can be written as

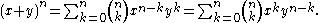
The final expression follows from the previous one by the symmetry of x and y in the first expression, and by comparison it follows that the sequence of binomial coefficients in the formula is symmetrical.

A variant of the binomial formula is obtained by substituting

Substitution (algebra)

In algebra, the operation of substitution can be applied in various contexts involving formal objects containing symbols ; the operation consists of systematically replacing occurrences of some symbol by a given value.A common case of substitution involves polynomials, where substitution of a...

 1 for x and x for y, so that it involves only a single variable

Variable (mathematics)

In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...

. In this form, the formula reads


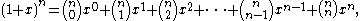
or equivalently

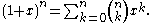
Examples

The most basic example of the binomial theorem is the formula for the square of x + y:


The binomial coefficients 1, 2, 1 appearing in this expansion correspond to the third row of Pascal's triangle. The coefficients of higher powers of x + y correspond to later rows of the triangle:

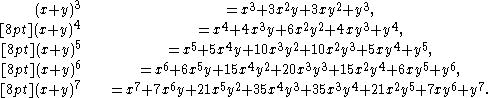
Notice that

1. the powers of x go down until it reaches 0 (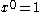),starting value is n (the n in .)
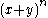2. the powers of y go up from 0 (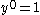) until it reaches n (also the n in .)
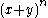3. the nth row of the Pascal's Triangle will be the coefficients of the expanded binomial.(Note that the top is row 0.)
4. the number of products is equal to
   1. the number of product groups is equal to
      The binomial theorem can be applied to the powers of any binomial. For example,
      
      
      For a binomial involving subtraction, the theorem can be applied as long as the opposite
      Additive inverse
      In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
      
       of the second term is used. This has the effect of changing the sign of every other term in the expansion:
      

      Geometrical explanation

      For positive values of a and b, the binomial theorem with n = 2 is the geometrically evident fact that a square of side can be cut into a square of side a, a square of side b, and two rectangles with sides a and b. With n = 3, the theorem states that a cube of side can be cut into a cube of side a, a cube of side b, three a×a×b rectangular boxes, and three a×b×b rectangular boxes.
      
      In calculus
      Calculus
      Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
      
      , this picture also gives a geometric proof of the derivative
      Derivative
      In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
      
        if one sets and 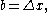interpreting b as an infinitesimal change in a, then this picture shows the infinitesimal change in the volume of an n-dimensional hypercube
      Hypercube
      In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
      
      , where the coefficient of the linear term (in 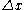) is the area of the n faces, each of dimension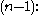
      Substituting this into the definition of the derivative via a difference quotient
      Difference quotient
      The primary vehicle of calculus and other higher mathematics is the function. Its "input value" is its argument, usually a point expressible on a graph...
      
       and taking limits means that the higher order terms – and higher – become negligible, and yields the formula interpreted as

      "the infinitesimal change in volume of an n-cube as side length varies is the area of n of its -dimensional faces".

      
      If one integrates this picture, which corresponds to applying the fundamental theorem of calculus
      Fundamental theorem of calculus
      The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
      
      , one obtains Cavalieri's quadrature formula, the integral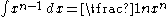 – see proof of Cavalieri's quadrature formula for details.
      

      The binomial coefficients

      The coefficients that appear in the binomial expansion are called binomial coefficients. These are usually written , and pronounced “n choose k”.
      

      Formulas

      The coefficient of x^n−ky^k is given by the formula
      ,
      
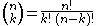      which is defined in terms of the factorial
      Factorial
      In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
      
       function n!. Equivalently, this formula can be written
      
      
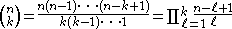
      with k factors in both the numerator and denominator of the fraction
      Fraction (mathematics)
      A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
      
      . Note that, although this formula involves a fraction, the binomial coefficient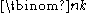 is actually an integer
      Integer
      The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
      
      .
      

      Combinatorial interpretation

      The binomial coefficient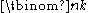 can be interpreted as the number of ways to choose k elements from an n-element set. This is related to binomials for the following reason: if we write (x + y)ⁿ as a product
      Product (mathematics)
      In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
      
      
      then, according to the distributive law, there will be one term in the expansion for each choice of either x or y from each of the binomials of the product. For example, there will only be one term xⁿ, corresponding to choosing x from each binomial. However, there will be several terms of the form xn−2y², one for each way of choosing exactly two binomials to contribute a y. Therefore, after combining like terms, the coefficient of xn−2y² will be equal to the number of ways to choose exactly 2 elements from an n-element set.
      

      Example

      The coefficient of xy² in
      
      
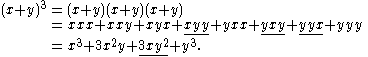
      equals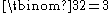 because there are three x,y strings of length 3 with exactly two ys, namely,
      
      
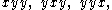
      corresponding to the three 2-element subsets of { 1, 2, 3 }, namely,
      
      
      where each subset specifies the positions of the y in a corresponding string.
      

      General case

      Expanding (x + y)ⁿ yields the sum of the 2 ⁿ products of the form e₁e₂ ... e _n where each e _i is x or y. Rearranging factors shows that each product equals x^n−ky^k for some k between 0 and n. For a given k, the following are proved equal in succession:
      • the number of copies of x^n − ky^k in the expansion
      • the number of n-character x,y strings having y in exactly k positions
      • the number of k-element subsets of { 1, 2, ..., n}
      • (this is either by definition, or by a short combinatorial argument if one is defining 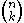as ).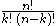
      
      This proves the binomial theorem.
      

      Inductive proof

      Induction
      Mathematical induction
      Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
      
       yields another proof of the binomial theorem (1). When n = 0, both sides equal 1, since x⁰ = 1 for all x and .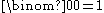
      Now suppose that (1) holds for a given n; we will prove it for n + 1.
      For j, k ≥ 0, let [ƒ(x, y)] _jk denote the coefficient of x^jy^k in the polynomial ƒ(x, y).
      By the inductive hypothesis, (x + y)ⁿ is a polynomial in x and y such that [(x + y)ⁿ] _jk is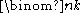 if j + k = n, and 0 otherwise.
      The identity
      
      
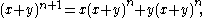
      shows that (x + y)ⁿ⁺¹ also is a polynomial in x and y, and
      
      
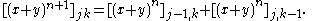
      If j + k = n + 1, then (j − 1) + k = n and j + (k − 1) = n, so the right hand side is
      
      
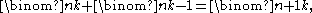
      by Pascal's identity. On the other hand, if j +k ≠ n + 1, then (j – 1) + k ≠ n and j +(k – 1) ≠ n, so we get 0 + 0 = 0. Thus
      
      
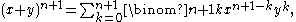
      which is the inductive hypothesis with n + 1 substituted for n and so completes the inductive step.
      

      Newton's generalised binomial theorem

      Around 1665, Isaac Newton
      Isaac Newton
      Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
      
       generalised the formula to allow real exponents other than nonnegative integers, and in fact it can be generalised further, to complex exponents. In this generalisation, the finite sum is replaced by an infinite series. In order to do this one needs to give meaning to binomial coefficients with an arbitrary upper index, which cannot be done using the above formula with factorials; however factoring out (n−k)! from numerator and denominator in that formula, and replacing n by r which now stands for an arbitrary number, one can define
      
      
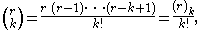
      where is the Pochhammer symbol
      Pochhammer symbol
      In mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
      
       here standing for a falling factorial. Then, if x and y are real numbers with |x| > |y|, and r is any complex number
      Complex number
      A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
      
      , one has
      
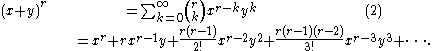
      When r is a nonnegative integer, the binomial coefficients for k > r are zero, so (2) specializes to (1), and there are at most r + 1 nonzero terms. For other values of r, the series (2) has infinitely many nonzero terms, at least if x and y are nonzero.
      
      This is important when one is working with infinite series and would like to represent them in terms of generalised hypergeometric functions.
      
      Taking r = −s leads to a useful but non-obvious formula:
      
      
      Further specializing to s = 1 yields the geometric series formula.
      

      Generalisations

      Formula (2) can be generalised to the case where x and y are complex numbers. For this version, one should assume |x| > |y| and define the powers of x + y and x using a holomorphic branch of log
      Complex logarithm
      In complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
      
       defined on an open disk of radius |x| centered at x.
      
      Formula (2) is valid also for elements x and y of a Banach algebra
      Banach algebra
      In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
      
       as long as xy = yx, x is invertible, and ||y/x|| < 1.
      

      The multinomial theorem

      The binomial theorem can be generalised to include powers of sums with more than two terms. The general version is
      
      
      where the summation is taken over all sequences of nonnegative integer indices k₁ through k_m such that the sum of all k_i is n. (For each term in the expansion, the exponents must add up to n). The coefficients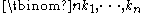 are known as multinomial coefficients, and can be computed by the formula
      
      
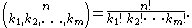
      Combinatorially, the multinomial coefficient counts the number of different ways to partition
      Partition of a set
      In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
      
       an n-element set into disjoint subset
      Subset
      In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
      
      s of sizes k₁, ..., k_n.
      

      The multi-binomial theorem

      It is often useful, when working in more dimension, to deal with products of binomial expressions. By the binomial theorem this is equal to
      
      
      This may be written more concisely, by multi-index notation
      Multi-index notation
      The mathematical notation of multi-indices simplifies formulae used in multivariable calculus, partial differential equations and the theory of distributions, by generalising the concept of an integer index to an ordered tuple of indices....
      
      , as
      
      

      Multiple angle identities

      For the complex numbers the binomial theorem can be combined with De Moivre's formula
      De Moivre's formula
      In mathematics, de Moivre's formula , named after Abraham de Moivre, states that for any complex number x and integer n it holds that...
      
       to yield multiple-angle formulas for the sine
      Sine
      In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
      
       and cosine. According to De Moivre's formula,
      Using the binomial theorem, the expression on the right can be expanded, and then the real and imaginary parts can be taken to yield formulas for cos(nx) and sin(nx). For example, since
      De Moivre's formula tells us that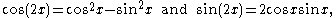
      which are the usual double-angle identities. Similarly, since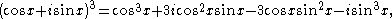
      De Moivre's formula yields
      In general,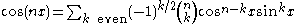
      and
      

      Series for e

      The number e
      E (mathematical constant)
      The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
      
       is often defined by the formula
      
      
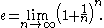
      Applying the binomial theorem to this expression yields the usual infinite series for e. In particular:
      
      
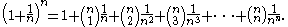
      The kth term of this sum is
      
      
      As n → ∞, the rational expression on the right approaches one, and therefore
      
      
      This indicates that e can be written as a series:
      
      
      Indeed, since each term of the binomial expansion is an increasing function
      Monotonic function
      In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
      
       of n, it follows from the monotone convergence theorem for series that the sum of this infinite series is equal to e.
      

      The binomial theorem in abstract algebra

      Formula (1) is valid more generally for any elements x and y of a semiring
      Semiring
      In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
      
       satisfying xy = yx. The theorem
      Theorem
      In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
      
       is true even more generally: alternativity
      Alternativity
      In abstract algebra, alternativity is a property of a binary operation. A magma G is said to be left alternative if y = x for all x and y in G and right alternative if y = x for all x and y in G...
      
       suffices in place of associativity
      Associativity
      In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
      
      .
      
      The binomial theorem can be stated by saying that the polynomial sequence
      Polynomial sequence
      In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
      
       { 1, x, x², x³, ... } is of binomial type.
      

      See also

      • Binomial distribution
      • Binomial probability
        Binomial probability
        Binomial probability typically deals with the probability of several successive decisions, each of which has two possible outcomes.- Definition :...
        
        
      • Binomial inverse theorem
        Binomial inverse theorem
        In mathematics, the Binomial Inverse Theorem is useful for expressing matrix inverses in different ways.If A, U, B, V are matrices of sizes p×p, p×q, q×q, q×p, respectively, then...
        
        
      • Binomial series
        Binomial series
        In mathematics, the binomial series is the Taylor series at x = 0 of the function f given by f =  α, where is an arbitrary complex number...
        
        
      • Combination
        Combination
        In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
        
        
      • Stirling's approximation
        Stirling's approximation
        In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
        
        
      • Multinomial theorem
        Multinomial theorem
        In mathematics, the multinomial theorem says how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem to polynomials.-Theorem:...
        
        
      • Negative binomial distribution
        Negative binomial distribution
        In probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
        
        
      • Pascal's triangle
        Pascal's triangle
        In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
        
        
      • Binomial approximation
        Binomial approximation
        The binomial approximation is useful for approximately calculating powers of numbers close to 1. It states that if x is a real number close to 0 and \alpha is a real number, then...
        
        
      
      

      External links

      • Binomial Theorem by Stephen Wolfram
        Stephen Wolfram
        Stephen Wolfram is a British scientist and the chief designer of the Mathematica software application and the Wolfram Alpha computational knowledge engine.- Biography :...
        
        , and "Binomial Theorem (Step-by-Step)" by Bruce Colletti and Jeff Bryant, Wolfram Demonstrations Project
        Wolfram Demonstrations Project
        The Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
        
        , 2007.
      • Binomial Theorem Introduction
      The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.