Madhava of Sangamagrama
Encyclopedia
Mādhava of Sañgamāgrama (c. 1350 – c. 1425) was a prominent Kerala mathematician
-astronomer from the town of Irińńālakkuţa
near Cochin, Kerala
, India
. He is considered the founder of the Kerala School of Astronomy and Mathematics. He was the first to have developed infinite series approximations for a range of trigonometric functions, which has been called the "decisive step onward from the finite procedures of ancient mathematics to treat their limit
-passage to infinity
". His discoveries opened the doors to what has today come to be known as Mathematical Analysis
. One of the greatest mathematician-astronomers of the Middle Ages
, Mādhavan made pioneering contributions to the study of infinite series, calculus
, trigonometry
, geometry
and algebra
.
Some scholars have also suggested that Mādhava's work, through the writings of the Kerala school, may have been transmitted to Europe via Jesuit missionaries and traders who were active around the ancient port of Muziris
at the time. As a result, it may have had an influence on later European developments in analysis and calculus.
, (who wrote a commentary on Veņwarõham
written by Mādhavan) bakuļam was locally known as "iraňňi". Dr. K.V. Sarma, an authority on Mādhavan has the opinion that the house name is either Irińńāŗappiļļy or Iriññinavaļļy'.
Irinjalakuda was once known as 'Irińńāţikuţal'. Sangamagrāmam
(lit. sangamam = union, grāmam = village) is a rough translation to Sanskrit from Dravidian word 'Irińńāţikuţal', which means 'iru (two) ańńāţi (market) kǖţal (union)' or the union of two markets.
c.1300, a set of fragmentary results), it is clear from citations that Madhava provided the creative impulse for the development of a rich mathematical tradition in medieval Kerala.
However, most of Madhava's original work (except a couple of them) is lost. He is referred to in the work of subsequent Kerala mathematicians, particularly in Nilakantha Somayaji
's Tantrasangraha (c.1500), as the source for several infinite series expansions, including sinθ and arctanθ. The 16th c. text Mahajyānayana prakāra cites Madhava as the source for several series derivations for π. In Jyeṣṭhadeva's Yuktibhāṣā
(c.1530), written in Malayalam
, these series are presented with proofs in terms of the Taylor series
expansions for polynomials like 1/(1+x2), with x = tan θ, etc.
Thus, what is explicitly Mādhava's work is a source of some debate. The Yukti-dipika (also called the Tantrasangraha-vyakhya), possibly composed Sankara Variyar, a student of Jyeṣṭhadeva, presents several versions of the series expansions for sin θ, cos θ, and arctan θ, as well as some products with radius and arclength, most versions of which appear in Yuktibhāṣā. For those that do not, Rajagopal and Rangachari have argued, quoting extensively from the original Sanskrit, that since some of these have been attributed by Nilakantha to Madhava, possibly some of the other forms might also be the work of Madhava.
Others have speculated that the early text Karanapaddhati
(c.1375-1475), or the Mahajyānayana prakāra might have been written by Madhava, but this is unlikely.
Karanapaddhati, along with
the even earlier Keralese mathematics text Sadratnamala, as well as the Tantrasangraha and Yuktibhāṣā, were considered in an 1834 article by Charles Matthew Whish, which was the first to draw attention to their priority over Newton in discovering the Fluxion
(Newton's name for differentials). In the mid-20th century, the Russian scholar Jushkevich revisited the legacy of Madhava, and a comprehensive look at the Kerala school was provided by Sarma in 1972
 There are several known Astronomers who preceded Mādhavan, including Kǖţalur Kizhār (2ns Century. Ref: Purananuru 229), Vararuci (4th Century), Sankaranarayana (866 AD). It is possible that other unknown figures may have preceded him. However, we have a clearer record of the tradition after Mādhavan. Parameshvara Namboodri was a direct disciple. According to a palmleaf manuscript of a Malayalam commentary on the Surya Siddhanta
There are several known Astronomers who preceded Mādhavan, including Kǖţalur Kizhār (2ns Century. Ref: Purananuru 229), Vararuci (4th Century), Sankaranarayana (866 AD). It is possible that other unknown figures may have preceded him. However, we have a clearer record of the tradition after Mādhavan. Parameshvara Namboodri was a direct disciple. According to a palmleaf manuscript of a Malayalam commentary on the Surya Siddhanta
, Parameswara's son Damodara (c. 1400-1500) had both Nilakantha Somayaji as his disciples.Jyeshtadevan was the disciple of Nilakanda. Achyuta Pisharati
of
Trikkantiyur is mentioned as a disciple of Jyeṣṭhadeva, and
the grammarian Melpathur Narayana Bhattathiri
as his disciple.
the first such series were developed by James Gregory in 1667. Madhava's work is notable for the series, but what is truly remarkable is his estimate of an error term (or correction term). This implies that the limit nature of the infinite series was quite well understood by him. Thus, Madhava may have invented the ideas underlying infinite series expansions of functions, power series, Trigonometric series, and rational approximations of infinite series.
However, as stated above, which results are precisely Madhava's and which are those of his successors, are somewhat difficult to determine. The following presents a summary of results that have been attributed to Madhava by various scholars.
Among his many contributions, he discovered the infinite series for the trigonometric function
s of sine
, cosine, tangent and arctangent, and many methods for calculating the circumference
of a circle
. One of Madhava's series is known from the text Yuktibhāṣā
, which contains the derivation and proof of the power series for inverse tangent
, discovered by Madhava. In the text, Jyeṣṭhadeva describes the series in the following manner:
This yields
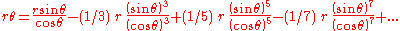
which further yields the result: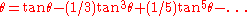
This series was traditionally known as the Gregory series (after James Gregory
, who discovered it three centuries after Madhava). Even if we consider this particular series as the work of Jyeṣṭhadeva, it would pre-date Gregory by a century, and certainly other infinite series of a similar nature had been worked out by Madhava. Today, it is referred to as the Madhava-Gregory-Leibniz series.
the following infinite series
expansion of π
, now known as the Madhava-Leibniz series:

which he obtained from the power series expansion of the arc-tangent function. However, what is most impressive is that he also gave a correction term, Rn, for the error after computing the sum up to n terms.
Madhava gave three forms of Rn which improved the approximation, namely
where the third correction leads to highly accurate computations of π.
It is not clear how Madhava might have found these correction terms. The most convincing is that they come as the first three convergents of a continued fraction which can itself be derived from the standard Indian approximation to π namely 62832/20000 (for the original 5th c. computation, see Aryabhata
).
He also gave a more rapidly converging series by transforming the original infinite series of π, obtaining the infinite series
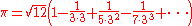
By using the first 21 terms to compute an approximation of π, he obtains a value correct to 11 decimal places (3.14159265359).
The value of
3.1415926535898, correct to 13 decimals, is sometimes attributed to Madhava,
but may be due to one of his followers. These were the most accurate approximations of π given since the 5th century (see History of numerical approximations of π).
The text Sadratnamala, usually considered as prior to Madhava, appears to give the astonishingly accurate value of π =3.14159265358979324 (correct to 17 decimal places). Based on this, R. Gupta has argued that this text may also have been composed by Madhava.
, discovered tests of convergence
of infinite series, and the analysis of infinite continued fraction
s.
He also discovered the solutions of transcendental equations
by iteration
, and found the approximation of transcendental number
s by continued fractions.
, which were further developed by his successors at the Kerala school of astronomy and mathematics. (It should be noted that certain ideas of calculus were known to earlier mathematicians
.) Madhava also extended some results found in earlier works, including those of Bhāskara II.
Madhava developed some components of Calculus
such as differentiation
, term by term integration
, iterative method
s for solutions of non-linear
equations, and the theory that the area under a curve is its integral.
which translates as the integration a variable (pada) equals half that
variable squared (varga); i.e. The integral of x dx is equal to
x2 / 2. This is clearly a start to the process of integral calculus.
A related result states that the area under a curve is its integral
. Most of these results pre-date similar results in Europe by several centuries.
In many senses,
Jyeshthadeva's Yuktibhāṣā
may be considered the world's first calculus
text.
The group also did much other work in astronomy; indeed many more pages are developed to astronomical computations than are for discussing analysis related results.
The Kerala school also contributed much to linguistics (the relation between language and mathematics is an ancient Indian tradition, see Katyayana
). The ayurvedic
and poetic traditions of Kerala
can also be traced back to this school. The famous poem, Narayaneeyam, was composed by Narayana Bhattathiri
.
"the founder of mathematical analysis; some of his discoveries in this field show him to have possessed extraordinary intuition.". O'Connor and Robertson state that a fair assessment of Madhava is that
he took the decisive step towards modern classical analysis.
. At the time, the port of Muziris
, near Sangamagrama
, was a major center for maritime trade, and a number of Jesuit missionaries and traders were active in this region. Given the fame of the Kerala school, and the interest shown by some of the Jesuit groups during this period in local scholarship, some scholars, including G. Joseph of the U. Manchester have suggested that the writings of the Kerala school may have also been transmitted to Europe around this time, which was still about a century before Newton. While no European translations have been discovered of these texts, it is possible that these ideas may still have had an influence on later European developments in analysis and calculus. (See Kerala school for more details).
This is due to wrong understanding of the authors concerned. It was almost impossible for the Jesuits in the sixteenth century, who are experts with the eminence of Mādhavan or his disciples, to study Sanskrit and Malayalam and to transmit them to European Mathematicians, instead of they themselves claiming the credit for the discovery.
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
-astronomer from the town of Irińńālakkuţa
Irinjalakuda
Irinjalakuda is a municipal town situated in the Thrissur district of Kerala, India. It is famous for the sprawling Koodalmanikyam Temple that has Bharata as the main deity and the St Thomas Cathedral in the heart of the City...
near Cochin, Kerala
Kerala
or Keralam is an Indian state located on the Malabar coast of south-west India. It was created on 1 November 1956 by the States Reorganisation Act by combining various Malayalam speaking regions....
, India
India
India , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
. He is considered the founder of the Kerala School of Astronomy and Mathematics. He was the first to have developed infinite series approximations for a range of trigonometric functions, which has been called the "decisive step onward from the finite procedures of ancient mathematics to treat their limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
-passage to infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
". His discoveries opened the doors to what has today come to be known as Mathematical Analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
. One of the greatest mathematician-astronomers of the Middle Ages
Middle Ages
The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
, Mādhavan made pioneering contributions to the study of infinite series, calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
Some scholars have also suggested that Mādhava's work, through the writings of the Kerala school, may have been transmitted to Europe via Jesuit missionaries and traders who were active around the ancient port of Muziris
Muziris
Muziris is an ancient sea-port in Southwestern India on the Periyar River 3.2 km from its mouth. The derivation of the name Muziris is said to be from "Mucciripattanam," "mucciri" means "cleft palate" and "pattanam" means "city". Near Muziris, Periyar River was branched into two like a...
at the time. As a result, it may have had an influence on later European developments in analysis and calculus.
Name
Mādhavan was born as Irińńaŗappiļļy or Iriññinavaļļi Mādhavan Namboodiri. He had written that his house name was related to the Vihar where a plant called "bakuļam" was planted. According to Achyuta PisharatiAchyuta Pisharati
Acyuta Piṣāraṭi was an Sanskrit grammarian, astrologer, astronomer and mathematician who studied under Jyeṣṭhadeva and was a member of Mādhava of Sañgamāgrama's Kerala school of astronomy and mathematics...
, (who wrote a commentary on Veņwarõham
Venvaroha
Veṇvāroha is a work in Sanskrit composed by Mādhava of Sangamagrāma the founder of the Kerala school of astronomy and mathematics. It is a work in 74 verses describing methods for the computation of the true positions of the Moon at intervals of about half an hour for various days in an...
written by Mādhavan) bakuļam was locally known as "iraňňi". Dr. K.V. Sarma, an authority on Mādhavan has the opinion that the house name is either Irińńāŗappiļļy or Iriññinavaļļy'.
Irinjalakuda was once known as 'Irińńāţikuţal'. Sangamagrāmam
Sangamagrama
Sangamagrama is a town in medieval Kerala believed to be the town ofIrinjalakuda, near Cochin. It is associated with the noted mathematician Madhava of Sangamagrama, founder of the Kerala school of mathematics.It is known for the Koodalmanikyam temple....
(lit. sangamam = union, grāmam = village) is a rough translation to Sanskrit from Dravidian word 'Irińńāţikuţal', which means 'iru (two) ańńāţi (market) kǖţal (union)' or the union of two markets.
Historiography
Although there is some evidence of Mathematical work in Kerala prior to Madhava (e.g. SadratnamalaSadratnamala
Sadratnamala is an astronomical-mathematical treatise in Sanskrit written by Sankara Varman, an astronomer-mathematician of the Kerala school of mathematics, in 1819. Even though the book has been written at a time when western mathematics and astronomy had been introduced in India, it is composed...
c.1300, a set of fragmentary results), it is clear from citations that Madhava provided the creative impulse for the development of a rich mathematical tradition in medieval Kerala.
However, most of Madhava's original work (except a couple of them) is lost. He is referred to in the work of subsequent Kerala mathematicians, particularly in Nilakantha Somayaji
Nilakantha Somayaji
Kelallur Nilakantha Somayaji was a major mathematician and astronomer of the Kerala school of astronomy and mathematics. One of his most influential works was the comprehensive astronomical treatise Tantrasamgraha completed in 1501...
's Tantrasangraha (c.1500), as the source for several infinite series expansions, including sinθ and arctanθ. The 16th c. text Mahajyānayana prakāra cites Madhava as the source for several series derivations for π. In Jyeṣṭhadeva's Yuktibhāṣā
Yuktibhasa
Yuktibhāṣā also known as Gaṇitanyāyasaṅgraha , is a major treatise on mathematics and astronomy, written by Indian astronomer Jyesthadeva of the Kerala school of mathematics in about AD 1530...
(c.1530), written in Malayalam
Malayalam language
Malayalam , is one of the four major Dravidian languages of southern India. It is one of the 22 scheduled languages of India with official language status in the state of Kerala and the union territories of Lakshadweep and Pondicherry. It is spoken by 35.9 million people...
, these series are presented with proofs in terms of the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansions for polynomials like 1/(1+x2), with x = tan θ, etc.
Thus, what is explicitly Mādhava's work is a source of some debate. The Yukti-dipika (also called the Tantrasangraha-vyakhya), possibly composed Sankara Variyar, a student of Jyeṣṭhadeva, presents several versions of the series expansions for sin θ, cos θ, and arctan θ, as well as some products with radius and arclength, most versions of which appear in Yuktibhāṣā. For those that do not, Rajagopal and Rangachari have argued, quoting extensively from the original Sanskrit, that since some of these have been attributed by Nilakantha to Madhava, possibly some of the other forms might also be the work of Madhava.
Others have speculated that the early text Karanapaddhati
Karanapaddhati
Karanapaddhati is an astronomical treatise in Sanskrit attributed to Puthumana Somayaji, an astronomer-mathematician of the Kerala school of astronomy and mathematics. The period of composition of the work is uncertain. C.M. Whish, a civil servant of the East India Company, brought this work to the...
(c.1375-1475), or the Mahajyānayana prakāra might have been written by Madhava, but this is unlikely.
Karanapaddhati, along with
the even earlier Keralese mathematics text Sadratnamala, as well as the Tantrasangraha and Yuktibhāṣā, were considered in an 1834 article by Charles Matthew Whish, which was the first to draw attention to their priority over Newton in discovering the Fluxion
Method of Fluxions
Method of Fluxions is a book by Isaac Newton. The book was completed in 1671, and published in 1736. Fluxions is Newton's term for differential calculus...
(Newton's name for differentials). In the mid-20th century, the Russian scholar Jushkevich revisited the legacy of Madhava, and a comprehensive look at the Kerala school was provided by Sarma in 1972
Lineage

Surya Siddhanta
The Surya Siddhanta is one of the earliest siddhanta in archeo-astronomy of the Hindus by an unknown author. It describes the archeo-astronomy theories, principles and methods of the ancient Hindus. This siddhanta is supposed to be the knowledge that the Sun god gave to an Asura called Maya. Asuras...
, Parameswara's son Damodara (c. 1400-1500) had both Nilakantha Somayaji as his disciples.Jyeshtadevan was the disciple of Nilakanda. Achyuta Pisharati
Achyuta Pisharati
Acyuta Piṣāraṭi was an Sanskrit grammarian, astrologer, astronomer and mathematician who studied under Jyeṣṭhadeva and was a member of Mādhava of Sañgamāgrama's Kerala school of astronomy and mathematics...
of
Trikkantiyur is mentioned as a disciple of Jyeṣṭhadeva, and
the grammarian Melpathur Narayana Bhattathiri
Melpathur Narayana Bhattathiri
Melpathur Narayana Bhattathiri , third student of Achyuta Pisharati, was of Madhava of Sangamagrama's Kerala school of astronomy and mathematics. He was a mathematical linguist . His most important scholarly work, Prkriya-sarvawom, sets forth an axiomatic system elaborating on the classical system...
as his disciple.
Contributions
If we consider mathematics as a progression from finite processes of algebra to considerations of the infinite, then the first steps towards this transition typically come with infinite series expansions. It is this transition to the infinite series that is attributed to Madhava. In Europe,the first such series were developed by James Gregory in 1667. Madhava's work is notable for the series, but what is truly remarkable is his estimate of an error term (or correction term). This implies that the limit nature of the infinite series was quite well understood by him. Thus, Madhava may have invented the ideas underlying infinite series expansions of functions, power series, Trigonometric series, and rational approximations of infinite series.
However, as stated above, which results are precisely Madhava's and which are those of his successors, are somewhat difficult to determine. The following presents a summary of results that have been attributed to Madhava by various scholars.
Infinite series
Main article : Madhava seriesMadhava series
In mathematics, a Madhava series is any one of the series in a collection of infinite series expressions all of which are believed to have been discovered by Sangamagrama Madhava the founder of the Kerala school of astronomy and mathematics...
Among his many contributions, he discovered the infinite series for the trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s of sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
, cosine, tangent and arctangent, and many methods for calculating the circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
. One of Madhava's series is known from the text Yuktibhāṣā
Yuktibhasa
Yuktibhāṣā also known as Gaṇitanyāyasaṅgraha , is a major treatise on mathematics and astronomy, written by Indian astronomer Jyesthadeva of the Kerala school of mathematics in about AD 1530...
, which contains the derivation and proof of the power series for inverse tangent
Inverse trigonometric function
In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions with suitably restricted domains .The notations sin−1, cos−1, etc...
, discovered by Madhava. In the text, Jyeṣṭhadeva describes the series in the following manner:
This yields
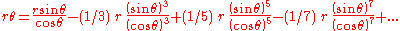
which further yields the result:
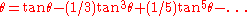
This series was traditionally known as the Gregory series (after James Gregory
James Gregory (astronomer and mathematician)
James Gregory FRS was a Scottish mathematician and astronomer. He described an early practical design for the reflecting telescope – the Gregorian telescope – and made advances in trigonometry, discovering infinite series representations for several trigonometric functions.- Biography :The...
, who discovered it three centuries after Madhava). Even if we consider this particular series as the work of Jyeṣṭhadeva, it would pre-date Gregory by a century, and certainly other infinite series of a similar nature had been worked out by Madhava. Today, it is referred to as the Madhava-Gregory-Leibniz series.
Trigonometry
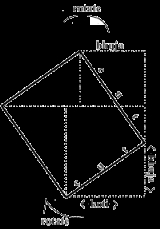
Madhava also gave a most accurate table of sines, defined in terms of the values of the half-sine chords for twenty-four arcs drawn at equal intervals in a quarter of a given circle. It is believed that he may have found these highly accurate tables based on these series expansions:- sin q = q - q3/3! + q5/5! - ...
- cos q = 1 - q2/2! + q4/4! - ...
The value of π (pi)
We find Madhava's work on the value of π cited in the Mahajyānayana prakāra ("Methods for the great sines"). While some scholars such as Sarma feel that this book may have been composed by Madhava himself, it is more likely the work of a 16th century successor. This text attributes most of the expansions to Madhava, and givesthe following infinite series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
expansion of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, now known as the Madhava-Leibniz series:

which he obtained from the power series expansion of the arc-tangent function. However, what is most impressive is that he also gave a correction term, Rn, for the error after computing the sum up to n terms.
Madhava gave three forms of Rn which improved the approximation, namely
- Rn = 1/(4n), or
- Rn = n/ (4n2 + 1), or
- Rn = (n2 + 1) / (4n3 + 5n).
where the third correction leads to highly accurate computations of π.
It is not clear how Madhava might have found these correction terms. The most convincing is that they come as the first three convergents of a continued fraction which can itself be derived from the standard Indian approximation to π namely 62832/20000 (for the original 5th c. computation, see Aryabhata
Aryabhata
Aryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
).
He also gave a more rapidly converging series by transforming the original infinite series of π, obtaining the infinite series
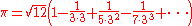
By using the first 21 terms to compute an approximation of π, he obtains a value correct to 11 decimal places (3.14159265359).
The value of
3.1415926535898, correct to 13 decimals, is sometimes attributed to Madhava,
but may be due to one of his followers. These were the most accurate approximations of π given since the 5th century (see History of numerical approximations of π).
The text Sadratnamala, usually considered as prior to Madhava, appears to give the astonishingly accurate value of π =3.14159265358979324 (correct to 17 decimal places). Based on this, R. Gupta has argued that this text may also have been composed by Madhava.
Algebra
Madhava also carried out investigations into other series for arclengths and the associated approximations to rational fractions of π, found methods of polynomial expansionPolynomial expansion
In mathematics, an expansion of a product of sums expresses it as a sum of products by using the fact that multiplication distributes over addition...
, discovered tests of convergence
Integral test for convergence
In mathematics, the integral test for convergence is a method used to test infinite series of non-negative terms for convergence. An early form of the test of convergence was developed in India by Madhava in the 14th century, and by his followers at the Kerala School...
of infinite series, and the analysis of infinite continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s.
He also discovered the solutions of transcendental equations
Transcendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
by iteration
Iteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
, and found the approximation of transcendental number
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
s by continued fractions.
Calculus
Madhava laid the foundations for the development of calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, which were further developed by his successors at the Kerala school of astronomy and mathematics. (It should be noted that certain ideas of calculus were known to earlier mathematicians
History of calculus
Calculus, historically known as infinitesimal calculus, is a mathematical discipline focused on limits, functions, derivatives, integrals, and infinite series. Ideas leading up to the notions of function, derivative, and integral were developed throughout the 17th century, but the decisive step was...
.) Madhava also extended some results found in earlier works, including those of Bhāskara II.
Madhava developed some components of Calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
such as differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
, term by term integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
, iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
s for solutions of non-linear
Nonlinearity
In mathematics, a nonlinear system is one that does not satisfy the superposition principle, or one whose output is not directly proportional to its input; a linear system fulfills these conditions. In other words, a nonlinear system is any problem where the variable to be solved for cannot be...
equations, and the theory that the area under a curve is its integral.
Madhava's works
K.V. Sarma has identified Madhava as the author of the following works:- Golavada
- Madhyamanayanaprakara
- Mahajyanayanaprakara
- Lagnaprakarana
- VenvarohaVenvarohaVeṇvāroha is a work in Sanskrit composed by Mādhava of Sangamagrāma the founder of the Kerala school of astronomy and mathematics. It is a work in 74 verses describing methods for the computation of the true positions of the Moon at intervals of about half an hour for various days in an...
- Sphutacandrapti
- Aganita-grahacara
- CandravakyaniCandravakyasCandravākyās are a collection of numbers, arranged in the form of a list, related to the motion of the Moon in its orbit around the Earth. These numbers are couched in the katapayadi system of representation of numbers and so apparently appear like a list of words, or phrases or short sentences...
Kerala School of Astronomy and Mathematics
The Kerala school of astronomy and mathematics flourished for at least two centuries beyond Madhava. In Jyeṣṭhadeva we find the notion of integration, termed sankalitam, (lit. collection), as in the statement:- ekadyekothara pada sankalitam samam padavargathinte pakuti,
which translates as the integration a variable (pada) equals half that
variable squared (varga); i.e. The integral of x dx is equal to
x2 / 2. This is clearly a start to the process of integral calculus.
A related result states that the area under a curve is its integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
. Most of these results pre-date similar results in Europe by several centuries.
In many senses,
Jyeshthadeva's Yuktibhāṣā
Yuktibhasa
Yuktibhāṣā also known as Gaṇitanyāyasaṅgraha , is a major treatise on mathematics and astronomy, written by Indian astronomer Jyesthadeva of the Kerala school of mathematics in about AD 1530...
may be considered the world's first calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
text.
The group also did much other work in astronomy; indeed many more pages are developed to astronomical computations than are for discussing analysis related results.
The Kerala school also contributed much to linguistics (the relation between language and mathematics is an ancient Indian tradition, see Katyayana
Katyayana
Kātyāyana was a Sanskrit grammarian, mathematician and Vedic priest who lived in ancient India.-Works:He is known for two works:...
). The ayurvedic
Ayurveda
Ayurveda or ayurvedic medicine is a system of traditional medicine native to India and a form of alternative medicine. In Sanskrit, words , meaning "longevity", and , meaning "knowledge" or "science". The earliest literature on Indian medical practice appeared during the Vedic period in India,...
and poetic traditions of Kerala
Kerala
or Keralam is an Indian state located on the Malabar coast of south-west India. It was created on 1 November 1956 by the States Reorganisation Act by combining various Malayalam speaking regions....
can also be traced back to this school. The famous poem, Narayaneeyam, was composed by Narayana Bhattathiri
Melpathur Narayana Bhattathiri
Melpathur Narayana Bhattathiri , third student of Achyuta Pisharati, was of Madhava of Sangamagrama's Kerala school of astronomy and mathematics. He was a mathematical linguist . His most important scholarly work, Prkriya-sarvawom, sets forth an axiomatic system elaborating on the classical system...
.
Influence
Madhava has been called "the greatest mathematician-astronomer of medieval India", or as"the founder of mathematical analysis; some of his discoveries in this field show him to have possessed extraordinary intuition.". O'Connor and Robertson state that a fair assessment of Madhava is that
he took the decisive step towards modern classical analysis.
Possible propagation to Europe
The Kerala school was well known in the 15th-16th c., in the period of the first contact with European navigators in the Malabar CoastMalabar Coast
The Malabar Coast is a long and narrow coastline on the south-western shore line of the mainland Indian subcontinent. Geographically, it comprises the wettest regions of southern India, as the Western Ghats intercept the moisture-laden monsoon rains, especially on their westward-facing mountain...
. At the time, the port of Muziris
Muziris
Muziris is an ancient sea-port in Southwestern India on the Periyar River 3.2 km from its mouth. The derivation of the name Muziris is said to be from "Mucciripattanam," "mucciri" means "cleft palate" and "pattanam" means "city". Near Muziris, Periyar River was branched into two like a...
, near Sangamagrama
Sangamagrama
Sangamagrama is a town in medieval Kerala believed to be the town ofIrinjalakuda, near Cochin. It is associated with the noted mathematician Madhava of Sangamagrama, founder of the Kerala school of mathematics.It is known for the Koodalmanikyam temple....
, was a major center for maritime trade, and a number of Jesuit missionaries and traders were active in this region. Given the fame of the Kerala school, and the interest shown by some of the Jesuit groups during this period in local scholarship, some scholars, including G. Joseph of the U. Manchester have suggested that the writings of the Kerala school may have also been transmitted to Europe around this time, which was still about a century before Newton. While no European translations have been discovered of these texts, it is possible that these ideas may still have had an influence on later European developments in analysis and calculus. (See Kerala school for more details).
This is due to wrong understanding of the authors concerned. It was almost impossible for the Jesuits in the sixteenth century, who are experts with the eminence of Mādhavan or his disciples, to study Sanskrit and Malayalam and to transmit them to European Mathematicians, instead of they themselves claiming the credit for the discovery.
See also
- Madhava's sine tableMadhava's sine tableMadhava's sine table is the table of trigonometric sines of various angles constructed by the 14th century Kerala mathematician-astronomer Madhava of Sangamagrama. The table lists the trigonometric sines of the twenty-four angles 3.75°, 7.50°, 11.25°, ... , and 90.00°...
- Madhava seriesMadhava seriesIn mathematics, a Madhava series is any one of the series in a collection of infinite series expressions all of which are believed to have been discovered by Sangamagrama Madhava the founder of the Kerala school of astronomy and mathematics...
- VenvarohaVenvarohaVeṇvāroha is a work in Sanskrit composed by Mādhava of Sangamagrāma the founder of the Kerala school of astronomy and mathematics. It is a work in 74 verses describing methods for the computation of the true positions of the Moon at intervals of about half an hour for various days in an...
- Indian mathematicsIndian mathematicsIndian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
- List of Indian mathematicians
- Kerala school of astronomy and mathematics
- History of calculusHistory of calculusCalculus, historically known as infinitesimal calculus, is a mathematical discipline focused on limits, functions, derivatives, integrals, and infinite series. Ideas leading up to the notions of function, derivative, and integral were developed throughout the 17th century, but the decisive step was...
- Ganita-yukti-bhasaGanita-yukti-bhasaGanita-yukti-bhasa is either the title or a part of the title of three different books:*Ganita-yukti-bhasa of Jyesthadeva, published by Springer, is the first critical edition with an English translation of Yuktibhasa, a seminal treatise in the Malayalam language composed in c.1530 CE by...

