
Manifold
Encyclopedia
.jpg)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
(specifically in differential geometry and topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
), a manifold is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that on a small enough scale resembles the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
of a specific dimension, called the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
of the manifold.
Thus, a line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
and a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
are one-dimensional manifolds, a plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
and sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
(the surface of a ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
) are two-dimensional manifolds, and so on into high-dimensional space. More formally, every point of an n-dimensional manifold has a neighborhood homeomorphic to an open subset of the n-dimensional space Rn.
Although manifolds resemble Euclidean spaces near each point ("locally"), the global structure of a manifold may be more complicated. For example, any point on the usual two-dimensional surface of a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
is surrounded by a circular region that can be flattened to a circular region of the plane, as in a geographical map. However, the sphere differs from the plane "in the large": in the language of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, they are not homeomorphic. The structure of a manifold is encoded by a collection of charts that form an atlas
Atlas (topology)
In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
, in analogy with an atlas consisting of charts of the surface of the Earth.
The concept of manifolds is central to many parts of geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and modern mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
because it allows more complicated structures to be expressed and understood in terms of the relatively well-understood properties of simpler spaces. For example, a manifold is typically endowed with a differentiable structure that allows one to do calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and a Riemannian metric that allows one to measure distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
s and angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s. Symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
s serve as the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
s in the Hamiltonian formalism
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, while four-dimensional Lorentzian manifolds model space-time in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
.
Circle
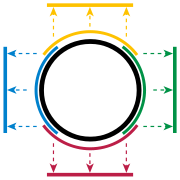
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
is the simplest example of a topological manifold. Topology ignores bending, so a small piece of a circle is treated exactly the same as a small piece of a line. Consider, for instance, the top half of the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
, x2 + y2 = 1, where the y-coordinate
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
is positive (indicated by the yellow arc in Figure 1). Any point of this semicircle can be uniquely described by its x-coordinate. So, projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
onto the first coordinate is a continuous, and invertible
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
, mapping from the upper semicircle to the open interval (−1,1):

Such functions along with the open regions they map are called charts. Similarly, there are charts for the bottom (red), left (blue), and right (green) parts of the circle. Together, these parts cover the whole circle and the four charts form an atlas
Atlas (topology)
In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
for the circle.
The top and right charts overlap: their intersection lies in the quarter of the circle where both the x- and the y-coordinates are positive. The two charts χtop and χright each map this part into the interval (0, 1). Thus a function T from (0, 1) to itself can be constructed, which first uses the inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of the top chart to reach the circle and then follows the right chart back to the interval. Let a be any number in (0, 1), then:

Such a function is called a transition map.
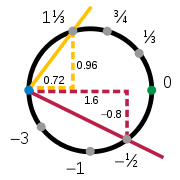
and
Here s is the slope of the line through the point at coordinates (x,y) and the fixed pivot point (−1, 0); t is the mirror image, with pivot point (+1, 0). The inverse mapping from s to (x, y) is given by
-

It can easily be confirmed that x2 + y2 = 1 for all values of the slope s. These two charts provide a second atlas for the circle, with
Each chart omits a single point, either (−1, 0) for s or (+1, 0) for t, so neither chart alone is sufficient to cover the whole circle. It can be proved that it is not possible to cover the full circle with a single chart. For example, although it is possible to construct a circle from a single line interval by overlapping and "gluing" the ends, this does not produce a chart; a portion of the circle will be mapped to both ends at once, losing invertibility.
Other curves
Manifolds need not be connected Connected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
Connected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
(all in "one piece"); an example is a pair of separate circles. In this example we see that a manifold need not have any well-defined notion of distance, for there is no way to define the distance between points that don't lie in the same piece.
Manifolds need not be closedClosed manifoldIn mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
; thus a line segment without its end points is a manifold. And they are never countable, unless the dimension of the manifold is 0. Putting these freedoms together, other examples of manifolds are a parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, a hyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
(two open, infinite pieces) and the locusLocus (mathematics)In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of points on a cubic curve y2 = x3−x (a closed loop piece and an open, infinite piece).
However, we exclude examples like two touching circles that share a point to form a figure-8; at the shared point we cannot create a satisfactory chart. Even with the bending allowed by topology, the vicinity of the shared point looks like a "+", not a line (a + is not homeomorphic to a closed interval (line segment) since deleting the center point from the + gives a space with four componentsLocally connected spaceIn topology and other branches of mathematics, a topological space X islocally connected if every point admits a neighbourhood basis consisting entirely of open, connected sets.-Background:...
(i.e., pieces) whereas deleting a point from a closed interval gives a space with at most two pieces; topological operationsHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
always preserve the number of pieces).
Enriched circle
Viewed using calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, the circle transition function T is simply a function between open intervals, which gives a meaning to the statement that T is differentiableDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. The transition map T, and all the others, are differentiable on (0, 1); therefore, with this atlas the circle is a differentiable manifoldDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
. It is also smooth and analytic because the transition functions have these properties as well.
Other circle properties allow it to meet the requirements of more specialized types of manifold. For example, the circle has a notion of distance between two points, the arc-length between the points; hence it is a Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
.
History
The study of manifolds combines many important areas of mathematics: it generalizes concepts such as curveCurveIn mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s and surfaces as well as ideas from linear algebraLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.
Early development
Before the modern concept of a manifold there were several important results.
Non-Euclidean geometryNon-Euclidean geometryNon-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
considers spaces where EuclidEuclidEuclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's parallel postulateParallel postulateIn geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
fails. Saccheri first studied them in 1733. LobachevskyNikolai Ivanovich LobachevskyNikolai Ivanovich Lobachevsky was a Russian mathematician and geometer, renowned primarily for his pioneering works on hyperbolic geometry, otherwise known as Lobachevskian geometry...
, BolyaiJános BolyaiJános Bolyai was a Hungarian mathematician, known for his work in non-Euclidean geometry.Bolyai was born in the Transylvanian town of Kolozsvár , then part of the Habsburg Empire , the son of Zsuzsanna Benkő and the well-known mathematician Farkas Bolyai.-Life:By the age of 13, he had mastered...
, and RiemannBernhard RiemannGeorg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
developed them 100 years later. Their research uncovered two types of spaces whose geometric structures differ from that of classical Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
; these gave rise to hyperbolic geometryHyperbolic geometryIn mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
and elliptic geometryElliptic geometryElliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
. In the modern theory of manifolds, these notions correspond to Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s with constant negative and positive curvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
, respectively.
Carl Friedrich GaussCarl Friedrich GaussJohann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
may have been the first to consider abstract spaces as mathematical objects in their own right. His theorema egregiumTheorema EgregiumGauss's Theorema Egregium is a foundational result in differential geometry proved by Carl Friedrich Gauss that concerns the curvature of surfaces...
gives a method for computing the curvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of a surfaceSurfaceIn mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
without considering the ambient spaceAmbient spaceAn ambient space, ambient configuration space, or electroambient space, is the space surrounding an object.-Mathematics:In mathematics, especially in geometry and topology, an ambient space is the space surrounding a mathematical object...
in which the surface lies. Such a surface would, in modern terminology, be called a manifold; and in modern terms, the theorem proved that the curvature of the surface is an intrinsic property. Manifold theory has come to focus exclusively on these intrinsic properties (or invariants), while largely ignoring the extrinsic properties of the ambient space.
Another, more topologicalTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
example of an intrinsic propertyTopological propertyIn topology and related areas of mathematics a topological property or topological invariant is a property of a topological space which is invariant under homeomorphisms. That is, a property of spaces is a topological property if whenever a space X possesses that property every space homeomorphic...
of a manifold is its Euler characteristicEuler characteristicIn mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
. Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
showed that for a convex polytopePolytopeIn elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
in the three-dimensional Euclidean space with V verticesVertex (geometry)In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
(or corners), E edges, and F faces,

The same formula will hold if we project the vertices and edges of the polytope onto a sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, creating a topological mapTopological mapIn cartography and geology, a topological map is one that has been simplified so that only vital information remains and unnecessary detail has been removed. These maps lack scale, and distance and direction are subject to change and variation, but the relationship between points is maintained...
with V vertices, E edges, and F faces, and in fact, will remain true for any spherical map, even if it does not arise from any convex polytope. Thus 2 is a topological invariant of the sphere, called its Euler characteristic. On the other hand, a torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
can be sliced open by its 'parallel' and 'meridian' circles, creating a map with V = 1 vertexVertex (geometry)In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
, E = 2 edges, and F = 1 face. Thus the Euler characteristic of the torus is 1 − 2 + 1 = 0. The Euler characteristic of other surfaces is a useful topological invariant, which can be extended to higher dimensions using Betti numberBetti numberIn algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s. In the mid nineteenth century, the Gauss–Bonnet theoremGauss–Bonnet theoremThe Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their geometry to their topology...
linked the Euler characteristic to the Gaussian curvature.
Synthesis
Investigations of Niels Henrik AbelNiels Henrik AbelNiels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
and Carl Gustav Jacobi on inversion of elliptic integralElliptic integralIn integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
s in the first half of 19th century led them to consider special types of complex manifoldComplex manifoldIn differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s, now known as JacobiansAbelian varietyIn mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
. Bernhard RiemannBernhard RiemannGeorg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
further contributed to their theory, clarifying the geometric meaning of the process of analytic continuationAnalytic continuationIn complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of functions of complex variables.
Another important source of manifolds in 19th century mathematics was analytical mechanicsAnalytical mechanicsAnalytical mechanics is a term used for a refined, mathematical form of classical mechanics, constructed from the 18th century onwards as a formulation of the subject as founded by Isaac Newton. Often the term vectorial mechanics is applied to the form based on Newton's work, to contrast it with...
, as developed by Simeon Poisson, Jacobi, and William Rowan HamiltonWilliam Rowan HamiltonSir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
. The possible states of a mechanical system are thought to be points of an abstract space, phase spacePhase spaceIn mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
in LagrangianLagrangian mechanicsLagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
and HamiltonianHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
formalisms of classical mechanics. This space is, in fact, a high-dimensional manifold, whose dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
corresponds to the degrees of freedom of the system and where the points are specified by their generalized coordinates. For an unconstrained movement of free particles the manifold is equivalent to the Euclidean space, but various conservation laws constrain it to more complicated formations, e.g. Liouville tori. The theory of a rotating solid body, developed in the 18th century by Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
and Joseph LagrangeJoseph LagrangeCount Joseph Lagrange was a French soldier who rose through the ranks and gained promotion to the rank of general officer during the French Revolutionary Wars, subsequently pursuing a successful career during the Napoleonic Wars and winning promotion to the top military rank of General of Division....
, gives another example where the manifold is nontrivial. Geometrical and topological aspects of classical mechanics were emphasized by Henri PoincaréHenri PoincaréJules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, one of the founders of topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.
Riemann was the first one to do extensive work generalizing the idea of a surface to higher dimensions. The name manifold comes from Riemann's original GermanGerman languageGerman is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
term, Mannigfaltigkeit, which William Kingdon CliffordWilliam Kingdon CliffordWilliam Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
translated as "manifoldness". In his Göttingen inaugural lecture, Riemann described the set of all possible values of a variable with certain constraints as a Mannigfaltigkeit, because the variable can have many values. He distinguishes between stetige Mannigfaltigkeit and diskrete Mannigfaltigkeit (continuous manifoldness and discontinuous manifoldness), depending on whether the value changes continuously or not. As continuous examples, Riemann refers to not only colors and the locations of objects in space, but also the possible shapes of a spatial figure. Using inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, Riemann constructs an n-fach ausgedehnte Mannigfaltigkeit (n times extended manifoldness or n-dimensional manifoldness) as a continuous stack of (n−1) dimensional manifoldnesses. Riemann's intuitive notion of a Mannigfaltigkeit evolved into what is today formalized as a manifold. Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s and Riemann surfaceRiemann surfaceIn mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s are named after Riemann.
Hermann WeylHermann WeylHermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
gave an intrinsic definition for differentiable manifolds in his lecture course on Riemann surfaces in 1911–1912, opening the road to the general concept of a topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that followed shortly. During the 1930s Hassler WhitneyHassler WhitneyHassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
and others clarified the foundationalFoundations of mathematicsFoundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...
aspects of the subject, and thus intuitions dating back to the latter half of the 19th century became precise, and developed through differential geometry and Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
theory. Notably, the Whitney embedding theorem showed that the intrinsic definition in terms of charts was equivalent to the extrinsic definition in terms of subsets of Euclidean space.
Topology of manifolds: highlights
Two-dimensional manifolds, also known as a 2D surfaces embedded in our common 3D space, were considered by Riemann under the guise of Riemann surfaceRiemann surfaceIn mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s, and rigorously classified in the beginning of the 20th century by Poul HeegaardPoul HeegaardPoul Heegaard was a Danish mathematician active in the field of topology. His 1898 thesis introduced a concept now called the Heegaard splitting of a 3-manifold. Heegaard's ideas allowed him to make a careful critique of work of Henri Poincaré...
and Max DehnMax DehnMax Dehn was a German American mathematician and a student of David Hilbert. He is most famous for his work in geometry, topology and geometric group theory...
. Henri PoincaréHenri PoincaréJules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
pioneered the study of three-dimensional manifolds and raised a fundamental question about them, today known as the Poincaré conjecturePoincaré conjectureIn mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
. After nearly a century of effort by many mathematicians, starting with Poincaré himself, a consensus among experts (as of 2006) is that Grigori PerelmanGrigori PerelmanGrigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
has proved the Poincaré conjecture (see the Solution of the Poincaré conjecture). Bill Thurston's geometrization programGeometrization conjectureThurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
, formulated in the 1970s, provided a far-reaching extension of the Poincaré conjecture to the general three-dimensional manifolds. Four-dimensional manifolds were brought to the forefront of mathematical research in the 1980s by Michael FreedmanMichael FreedmanMichael Hartley Freedman is a mathematician at Microsoft Station Q, a research group at the University of California, Santa Barbara. In 1986, he was awarded a Fields Medal for his work on the Poincaré conjecture. Freedman and Robion Kirby showed that an exotic R4 manifold exists.Freedman was born...
and in a different setting, by Simon DonaldsonSimon DonaldsonSimon Kirwan Donaldson FRS , is an English mathematician known for his work on the topology of smooth four-dimensional manifolds. He is now Royal Society research professor in Pure Mathematics and President of the Institute for Mathematical Science at Imperial College London...
, who was motivated by the then recent progress in theoretical physics (Yang-Mills theoryGauge theoryIn physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
), where they serve as a substitute for ordinary 'flat' space-time. Andrey Markov Jr.Andrey Markov (Soviet mathematician)Andrey Andreyevich Markov Jr. was a Soviet mathematician, the son of the great Russian mathematician Andrey Andreyevich Markov Sr, and one of the key founders of the Russian school of constructive mathematics and logic...
showed in 1960 that no algorithm exists for classifying four-dimensional manifolds. Important work on higher-dimensional manifolds, including analogues of the Poincaré conjectureGeneralized Poincaré conjectureIn the mathematical area of topology, the term Generalized Poincaré conjecture refers to a statement that a manifold which is a homotopy sphere 'is' a sphere. More precisely, one fixes a...
, had been done earlier by René ThomRené ThomRené Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...
, John MilnorJohn MilnorJohn Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
, Stephen SmaleStephen SmaleSteven Smale a.k.a. Steve Smale, Stephen Smale is an American mathematician from Flint, Michigan. He was awarded the Fields Medal in 1966, and spent more than three decades on the mathematics faculty of the University of California, Berkeley .-Education and career:He entered the University of...
and Sergei Novikov. One of the most pervasive and flexible techniques underlying much work on the topology of manifoldsDifferential topologyIn mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
is Morse theoryMorse theoryIn differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
.
Mathematical definition
Informally, a manifold is a spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that is "modeled on" Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
There are many different kinds of manifolds and generalizations.
In geometry and topologyGeometry and topologyIn mathematics, geometry and topology is an umbrella term for geometry and topology, as the line between these two is often blurred, most visibly in local to global theorems in Riemannian geometry, and results like the Gauss–Bonnet theorem and Chern–Weil theory.Sharp distinctions between geometry...
, all manifolds are topological manifoldTopological manifoldIn mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
s, possibly with additional structure, most often a differentiable structureDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
. In terms of constructing manifolds via patching, a manifold has an additional structure if the transition maps between different patches satisfy axioms beyond just continuity. For instance, differentiable manifoldDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s have homeomorphisms on overlapping neighborhoods diffeomorphic with each other, so that the manifold has a well-defined set of functions which are differentiable in each neighborhood, and so differentiable on the manifold as a whole.
Formally, a topological manifold is a second countable HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that is locally homeomorphic to Euclidean space.
Second countable and Hausdorff are point-set conditions;
second countable excludes spaces which are in some sense 'too large' such as the long lineLong line (topology)In topology, the long line is a topological space somewhat similar to the real line, but in a certain way "longer". It behaves locally just like the real line, but has different large-scale properties. Therefore it serves as one of the basic counterexamples of topology...
, while Hausdorff excludes spaces such as "the line with two origins" (these generalized manifolds are discussed in non-Hausdorff manifoldNon-Hausdorff manifoldIn mathematics, it is a usual axiom of a manifold to be a Hausdorff space, and this is assumed throughout geometry and topology: "manifold" means " Hausdorff manifold"....
s).
Locally homeomorphic to Euclidean space means that every point has a neighborhood homeomorphic to an open Euclidean n-ballBall (mathematics)In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
,

Generally manifolds are taken to have a fixed dimension (the space must be locally homeomorphic to a fixed n-ball), and such a space is called an n-manifold; however, some authors admit manifolds where different points can have different dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s. If a manifold has a fixed dimension, it is called a pure manifold. For example, the sphere has a constant dimension of 2 and is therefore a pure manifold whereas the disjoint unionDisjoint unionIn mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of a sphere and a line in three-dimensional space is not a pure manifold. Since dimension is a local invariant (i.e. the map sending each point to the dimension of its neighbourhood over which a chart is defined, is locally constant), each connected componentConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
has a fixed dimension.
Scheme-theoreticallyScheme (mathematics)In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
, a manifold is a locally ringed space, whose structure sheaf is locally isomorphic to the sheaf of continuous (or differentiable, or complex-analytic, etc.) functions on Euclidean space. This definition is mostly used when discussing analytic manifoldAnalytic manifoldIn mathematics, an analytic manifold is a topological manifold with analytic transition maps. Every complex manifold is an analytic manifold....
s in algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.
Broad definition
The broadest common definition of manifold is a topological space locally homeomorphic to a topological vector spaceTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
over the reals. This omits the point-set axioms, allowing higher cardinalities and non-Hausdorff manifoldNon-Hausdorff manifoldIn mathematics, it is a usual axiom of a manifold to be a Hausdorff space, and this is assumed throughout geometry and topology: "manifold" means " Hausdorff manifold"....
s; and it omits finite dimension, allowing structures such as Hilbert manifoldHilbert manifoldIn mathematics, a Hilbert manifold is a manifold modeled on Hilbert spaces. Thus it is a separable Hausdorff space in which each point has a neighbourhood homeomorphic to an infinite dimensional Hilbert space. The concept of a Hilbert manifold provides a possibility of extending the theory of...
s to be modeled on Hilbert spaces, Banach manifoldBanach manifoldIn mathematics, a Banach manifold is a manifold modeled on Banach spaces. Thus it is a topological space in which each point has a neighbourhood homeomorphic to an open set in a Banach space...
s to be modeled on Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s, and Fréchet manifoldFréchet manifoldIn mathematics, in particular in nonlinear analysis, a Fréchet manifold is a topological space modeled on a Fréchet space in much the same way as a manifold is modeled on a Euclidean space....
s to be modeled on Fréchet spaceFréchet spaceIn functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
s. Usually one relaxes one or the other condition: manifolds with the point-set axioms are studied in general topologyGeneral topologyIn mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
, while infinite-dimensional manifolds are studied in functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
.
Charts, atlases, and transition maps
- For more exact definitions, see Differentiable manifold#Definition.
The spherical Earth is navigated using flat maps or charts, collected in an atlas. Similarly, a differentiable manifold can be described using mathematical mapsMap (mathematics)In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
, called coordinate charts, collected in a mathematical atlas. It is not generally possible to describe a manifold with just one chart, because the global structure of the manifold is different from the simple structure of the charts. For example, no single flat map can represent the entire Earth without separation of adjacent features across the map's boundaries or duplication of coverage. When a manifold is constructed from multiple overlapping charts, the regions where they overlap carry information essential to understanding the global structure.
Charts
A coordinate map, a coordinate chart, or simply a chart, of a manifold is an invertible mapMap (mathematics)In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
between a subset of the manifold and a simple space such that both the map and its inverse preserve the desired structure. For a topological manifold, the simple space is some Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn and interest focuses on the topological structure. This structure is preserved by homeomorphisms, invertible maps that are continuous in both directions.
In the case of a differentiable manifoldDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
, a set of charts called an atlas allows us to do calculus on manifolds. Polar coordinates, for example, form a chart for the plane R2 minus the positive x-axis and the origin. Another example of a chart is the map χtop mentioned in the section above, a chart for the circle.
Atlases
The description of most manifolds requires more than one chart (a single chart is adequate for only the simplest manifolds). A specific collection of charts which covers a manifold is called an atlas. An atlas is not unique as all manifolds can be covered multiple ways using different combinations of charts. Two atlases are said to be Ck equivalent if their union is also a Ck atlas.
The atlas containing all possible charts consistent with a given atlas is called the maximal atlas (i.e. an equivalence class containing that given atlas (under the already defined equivalence relation given in the previous paragraph)). Unlike an ordinary atlas, the maximal atlas of a given manifold is unique. Though it is useful for definitions, it is an abstract object and not used directly (e.g. in calculations).
Transition maps
Charts in an atlas may overlap and a single point of a manifold may be represented in several charts. If two charts overlap, parts of them represent the same region of the manifold, just as a map of Europe and a map of Asia may both contain Moscow. Given two overlapping charts, a transition function can be defined which goes from an open ball in Rn to the manifold and then back to another (or perhaps the same) open ball in Rn. The resultant map, like the map T in the circle example above, is called a change of coordinates, a coordinate transformation, a transition function, or a transition map.
Additional structure
An atlas can also be used to define additional structure on the manifold. The structure is first defined on each chart separately. If all the transition maps are compatible with this structure, the structure transfers to the manifold.
This is the standard way differentiable manifolds are defined. If the transition functions of an atlas for a topological manifold preserve the natural differential structure of Rn (that is, if they are diffeomorphismDiffeomorphismIn mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s), the differential structure transfers to the manifold and turns it into a differentiable manifold. Complex manifoldComplex manifoldIn differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s are introduced in an analogous way by requiring that the transition functions of an atlas are holomorphic functions. For symplectic manifoldSymplectic manifoldIn mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
s, the transition functions must be symplectomorphismSymplectomorphismIn mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
s.
The structure on the manifold depends on the atlas, but sometimes different atlases can be said to give rise to the same structure. Such atlases are called compatible.
These notions are made precise in general through the use of pseudogroupPseudogroupIn mathematics, a pseudogroup is an extension of the group concept, but one that grew out of the geometric approach of Sophus Lie, rather than out of abstract algebra...
s.
Construction
A single manifold can be constructed in different ways, each stressing a different aspect of the manifold, thereby leading to a slightly different viewpoint.
Charts
Perhaps the simplest way to construct a manifold is the one used in the example above of the circle. First, a subset of R2 is identified, and then an atlas covering this subset is constructed. The concept of manifold grew historically from constructions like this. Here is another example, applying this method to the construction of a sphere:
Sphere with charts
A sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
can be treated in almost the same way as the circle. In mathematics a sphere is just the surface (not the solid interior), which can be defined as a subset of R3:
The sphere is two-dimensional, so each chart will map part of the sphere to an open subset of R2. Consider the northern hemisphere, which is the part with positive z coordinate (coloured red in the picture on the right). The function χ defined by
maps the northern hemisphere to the open unit disc by projecting it on the (x, y) plane. A similar chart exists for the southern hemisphere. Together with two charts projecting on the (x, z) plane and two charts projecting on the (y, z) plane, an atlas of six charts is obtained which covers the entire sphere.
This can be easily generalized to higher-dimensional spheres.
Patchwork
A manifold can be constructed by gluing together pieces in a consistent manner, making them into overlapping charts. This construction is possible for any manifold and hence it is often used as a characterisation, especially for differentiable and Riemannian manifolds. It focuses on an atlas, as the patches naturally provide charts, and since there is no exterior space involved it leads to an intrinsic view of the manifold.
The manifold is constructed by specifying an atlas, which is itself defined by transition maps. A point of the manifold is therefore an equivalence class of points which are mapped to each other by transition maps. Charts map equivalence classes to points of a single patch. There are usually strong demands on the consistency of the transition maps. For topological manifolds they are required to be homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s; if they are also diffeomorphismDiffeomorphismIn mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s, the resulting manifold is a differentiable manifold.
This can be illustrated with the transition map t = 1⁄s from the second half of the circle example. Start with two copies of the line. Use the coordinate s for the first copy, and t for the second copy. Now, glue both copies together by identifying the point t on the second copy with the point s = 1⁄t on the first copy (the points t = 0 and s = 0 are not identified with any point on the first and second copy, respectively). This gives a circle.
Intrinsic and extrinsic view
The first construction and this construction are very similar, but they represent rather different points of view. In the first construction, the manifold is seen as embeddedEmbeddingIn mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
in some Euclidean space. This is the extrinsic view. When a manifold is viewed in this way, it is easy to use intuition from Euclidean spaces to define additional structure. For example, in a Euclidean space it is always clear whether a vector at some point is tangential or normal to some surface through that point.
The patchwork construction does not use any embedding, but simply views the manifold as a topological space by itself. This abstract point of view is called the intrinsic view. It can make it harder to imagine what a tangent vector might be, and there is no intrinsic notion of a normal bundle, but instead there is an intrinsic stable normal bundleStable normal bundleIn surgery theory, a branch of mathematics, the stable normal bundle of a differentiable manifold is an invariant which encodes the stable normal data. There are analogs for generalizations of manifold, notably PL-manifolds and topological manifolds...
.
n-Sphere as a patchwork
The n-sphereHypersphereIn mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
Sn is a generalisation of the idea of a circle (1-sphere) and sphere (2-sphere) to higher dimensions. An n-sphere Sn can be constructed by gluing together two copies of Rn. The transition map between them is defined as
This function is its own inverse and thus can be used in both directions. As the transition map is a smooth functionSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
, this atlas defines a smooth manifold.
In the case n = 1, the example simplifies to the circle example given earlier.
Identifying points of a manifold
It is possible to define different points of a manifold to be same. This can be visualized as gluing these points together in a single point, forming a quotient spaceQuotient spaceIn topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
. There is, however, no reason to expect such quotient spaces to be manifolds. Among the possible quotient spaces that are not necessarily manifolds, orbifoldOrbifoldIn the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
s and CW complexCW complexIn topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es are considered to be relatively well-behavedWell-behavedMathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
. An example of a quotient space of a manifold that is also a manifold is the real projective spaceReal projective spaceIn mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
identified as a quotient space of the corresponding sphere.
One method of identifying points (gluing them together) is through a right (or left) action of a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, which actsGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on the manifold. Two points are identified if one is moved onto the other by some group element. If M is the manifold and G is the group, the resulting quotient space is denoted by M / G (or G \ M).
Manifolds which can be constructed by identifying points include tori and real projective spaceReal projective spaceIn mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
s (starting with a plane and a sphere, respectively).
Manifold with boundary
A manifold with boundary is a manifold with an edge. For example a sheet of paper with rounded corners is a 2-manifold with a 1-dimensional boundary. The boundary of an n-manifold with boundary is an (n − 1)-manifold. A diskDisk (mathematics)In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
(circle plus interior) is a 2-manifold with boundary. Its boundary is a circle, a 1-manifold. A ballBall (mathematics)In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
(sphere plus interior) is a 3-manifold with boundary. Its boundary is a sphere, a 2-manifold. (See also Boundary (topology)Boundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
).
In technical language, a manifold with boundary is a space containing both interior points and boundary points. Every interior point has a neighborhood homeomorphic to the open n-ball {(x1, x2, …, xn) | Σ xi2 < 1}. Every boundary point has a neighborhood homeomorphic to the "half" n-ball {(x1, x2, …, xn) | Σ xi2 < 1 and x1 ≥ 0}. The homeomorphism must send the boundary point to a point with x1 = 0.
Gluing along boundaries
Two manifolds with boundaries can be glued together along a boundary. If this is done the right way, the result is also a manifold. Similarly, two boundaries of a single manifold can be glued together.
Formally, the gluing is defined by a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the two boundaries. Two points are identified when they are mapped onto each other. For a topological manifold this bijection should be a homeomorphism, otherwise the result will not be a topological manifold. Similarly for a differentiable manifold it has to be a diffeomorphismDiffeomorphismIn mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
. For other manifolds other structures should be preserved.
A finite cylinder may be constructed as a manifold by starting with a strip [0, 1] × [0, 1] and gluing a pair of opposite edges on the boundary by a suitable diffeomorphism. A projective planeProjective planeIn mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
may be obtained by gluing a sphere with a hole in it to a Möbius stripMöbius stripThe Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
along their respective circular boundaries.
Cartesian products
The Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of manifolds is also a manifold.
The dimension of the product manifold is the sum of the dimensions of its factors. Its topology is the product topologyProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
, and a Cartesian product of charts is a chart for the product manifold. Thus, an atlas for the product manifold can be constructed using atlases for its factors. If these atlases define a differential structure on the factors, the corresponding atlas defines a differential structure on the product manifold. The same is true for any other structure defined on the factors. If one of the factors has a boundary, the product manifold also has a boundary. Cartesian products may be used to construct tori and finite cylinderCylinder (geometry)A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
s, for example, as S1 × S1 and S1 × [0, 1], respectively.

Topological manifolds
The simplest kind of manifold to define is the topological manifold, which looks locally like some "ordinary" Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn. Formally, a topological manifold is a topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
locally homeomorphicLocal homeomorphismIn mathematics, more specifically topology, a local homeomorphism is intuitively a function, f, between topological spaces that preserves local structure. Equivalently, one can cover the domain of this function by open sets, such that f restricted to each such open set is a homeomorphism onto its...
to a Euclidean space. This means that every point has a neighbourhood for which there exists a homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
(a bijectiveBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
continuous function whose inverse is also continuous) mapping that neighbourhood to Rn. These homeomorphisms are the charts of the manifold.
It is to be noted that a topological manifold looks locally like a Euclidean space in a rather weak manner: while for each individual chart it is possible to distinguish differentiable functions or measure distances and angles, merely by virtue of being a topological manifold a space does not have any particular and consistent choice of such concepts. In order to discuss such properties for a manifold, one needs to specify further structure and consider differentiable manifolds and Riemannian manifolds discussed below. In particular, the same underlying topological manifold can have several mutually incompatible classes of differentiable functions and an infinite number of ways to specify distances and angles.
Usually additional technical assumptions on the topological space are made to exclude pathological cases. It is customary to require that the space be HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
and second countableSecond-countable spaceIn topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
.
The dimension of the manifold at a certain point is the dimension of the Euclidean space that the charts at that point map to (number n in the definition). All points in a connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
manifold have the same dimension. Some authors require that all charts of a topological manifold map to Euclidean spaces of same dimension. In that case every topological manifold has a topological invariant, its dimension. Other authors allow disjoint unions of topological manifolds with differing dimensions to be called manifolds.
Differentiable manifolds
For most applications a special kind of topological manifold, a differentiable manifold, is used. If the local charts on a manifold are compatible in a certain sense, one can define directions, tangent spaces, and differentiable functions on that manifold. In particular it is possible to use calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
on a differentiable manifold. Each point of an n-dimensional differentiable manifold has a tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
. This is an n-dimensional Euclidean space consisting of the tangent vectors of the curves through the point.
Two important classes of differentiable manifolds are smooth and analytic manifoldAnalytic manifoldIn mathematics, an analytic manifold is a topological manifold with analytic transition maps. Every complex manifold is an analytic manifold....
s. For smooth manifolds the transition maps are smoothSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
, that is infinitely differentiable. Analytic manifolds are smooth manifolds with the additional condition that the transition maps are analyticAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
(they can be expressed as power series, which are essentially polynomials of infinite degree). The sphere can be given analytic structure, as can most familiar curves and surfaces.
A rectifiable setRectifiable setIn mathematics, a rectifiable set is a set that is smooth in a certain measure-theoretic sense. It is an extension of the idea of a rectifiable curve to higher dimensions; loosely speaking, a rectifiable set is a rigorous formulation of a piece-wise smooth set...
generalizes the idea of a piecewise smooth or rectifiable curve to higher dimensions; however, rectifiable sets are not in general manifolds.
Riemannian manifolds
To measure distances and angles on manifolds, the manifold must be Riemannian. A Riemannian manifold is a differentiable manifold in which each tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
is equipped with an inner productInner product spaceIn mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
〈⋅,⋅〉 in a manner which varies smoothly from point to point. Given two tangent vectors u and v, the inner product〈u,v〉gives a real number. The dotDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
(or scalar) product is a typical example of an inner product. This allows one to define various notions such as lengthLengthIn geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
, angleAngleIn geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s, areaAreaArea is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
s (or volumeVolumeVolume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
s), curvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
, gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
s of functions and divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s.
All differentiable manifolds (of constant dimension) can be given the structure of a Riemannian manifold. The Euclidean space itself carries a natural structure of Riemannian manifold (the tangent spaces are naturally identified with the Euclidean space itself and carry the standard scalar product of the space). Many familiar curves and surfaces, including for example all n-spheres, are specified as subspaces of a Euclidean space and inherit a metric from their embedding in it.
Finsler manifolds
A Finsler manifold allows the definition of distance but does not require the concept of angle; it is an analytic manifold in which each tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
is equipped with a norm, ||·||, in a manner which varies smoothly from point to point. This norm can be extended to a metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
, defining the length of a curve; but it cannot in general be used to define an inner product.
Any Riemannian manifold is a Finsler manifold.
Lie groups
Lie groups, named after Sophus LieSophus LieMarius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...
, are differentiable manifolds that carry also the structure of a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
which is such that the group operations are defined by smooth maps.
A Euclidean vector space with the group operation of vector addition is an example of a non-compact Lie group.
A simple example of a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Lie group is the circle: the group operation is simply rotation. This group, known as U(1), can be also characterised as the group of complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s of modulusAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
1 with multiplication as the group operation.
Other examples of Lie groups include special groups of matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, which are all subgroups of the general linear groupGeneral linear groupIn mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
, the group of n by n matrices with non-zero determinant. If the matrix entries are real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, this will be an n2-dimensional disconnected manifold. The orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
s, the symmetry groupSymmetry groupThe symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
s of the sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
and hypersphereHypersphereIn mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
s, are n(n-1)/2 dimensional manifolds, where n-1 is the dimension of the sphere. Further examples can be found in the table of Lie groupsTable of Lie groupsThis article gives a table of some common Lie groups and their associated Lie algebras.The following are noted: the topological properties of the group , as well as on their algebraic properties .For more examples of Lie groups and other...
.
Other types of manifolds
- A complex manifoldComplex manifoldIn differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
is a manifold modeled on Cn with holomorphic transition functions on chart overlaps. These manifolds are the basic objects of study in complex geometry. A one-complex-dimensional manifold is called a Riemann surfaceRiemann surfaceIn mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
. Note that an n-dimensional complex manifold has dimension 2n as a real differentiable manifold. - A CR manifoldCR manifoldIn mathematics, a CR manifold is a differentiable manifold together with a geometric structure modeled on that of a real hypersurface in a complex vector space, or more generally modeled on an edge of a wedge....
is a manifold modeled on boundaries of domains in Cn. - Infinite dimensional manifolds: to allow for infinite dimensions, one may consider Banach manifoldBanach manifoldIn mathematics, a Banach manifold is a manifold modeled on Banach spaces. Thus it is a topological space in which each point has a neighbourhood homeomorphic to an open set in a Banach space...
s which are locally homeomorphic to Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. Similarly, Fréchet manifolds are locally homeomorphic to Fréchet spaceFréchet spaceIn functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
s. - A symplectic manifoldSymplectic manifoldIn mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
is a kind of manifold which is used to represent the phase spaces in classical mechanicsClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. They are endowed with a 2-formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
that defines the Poisson bracketPoisson bracketIn mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
. A closely related type of manifold is a contact manifoldContact geometryIn mathematics, contact geometry is the study of a geometric structure on smooth manifolds given by a hyperplane distribution in the tangent bundle and specified by a one-form, both of which satisfy a 'maximum non-degeneracy' condition called 'complete non-integrability'...
. - A combinatorial manifold is a kind of manifold which is discretization of a manifold. It usually means a piecewise linear manifoldPiecewise linear manifoldIn mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions.An isomorphism of PL manifolds is called a PL...
made by simplicial complexes. - A digital manifoldDigital manifoldIn mathematics, a digital manifold is a special kind of combinatorial manifold which is defined in digital space i.e. grid cell space. A combinatorial manifold is a kind of manifold which is a discretization of a manifold. It usually means a piecewise linear manifold made by simplicial complexes.-...
is a special kind of combinatorial manifold which is defined in digital space. See digital topologyDigital topologyDigital topology deals with properties and features of two-dimensional or three-dimensional digital imagesthat correspond to topological properties or topological features of objects....
Classification and invariants
Different notions of manifolds have different notions of classification and invariant; in this section we focus on smooth closed manifolds.
The classification of smooth closed manifolds is well-understood in principle, except in dimension 44-manifoldIn mathematics, 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different...
: in low dimensions (2 and 3) it is geometric, via the uniformization theoremUniformization theoremIn mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
and the Solution of the Poincaré conjecture, and in high dimension (5 and above) it is algebraic, via surgery theorySurgery theoryIn mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
. This is a classification in principle: the general question of whether two smooth manifolds are diffeomorphic is not computable in general. Further, specific computations remain difficult, and there are many open questions.
Orientable surfaces can be visualized, and their diffeomorphism classes enumerated, by genus. Given two orientable surfaces, one can determine if they are diffeomorphic by computing their respective genera and comparing: they are diffeomorphic if and only if the genera are equal, so the genus forms a complete set of invariantsComplete set of invariantsIn mathematics, a complete set of invariants for a classification problem is a collection of mapsf_i : X \to Y_i \,, such that x ∼ x' if and only if f_i = f_i for all i...
.
This is much harder in higher dimensions: higher dimensional manifolds cannot be directly visualized (though visual intuition is useful in understanding them), nor can their diffeomorphism classes be enumerated, nor can one in general determine if two different descriptions of a higher-dimensional manifold refer to the same object.
However, one can determine if two manifolds are different if there is some intrinsic characteristic that differentiates them. Such criteria are commonly referred to as invariantsInvariant (mathematics)In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
, because, while they may be defined in terms of some presentation (such as the genus in terms of a triangulation), they are the same relative to all possible descriptions of a particular manifold: they are invariant under different descriptions.
Naively, one could hope to develop an arsenal of invariant criteria that would definitively classify all manifolds up to isomorphism. Unfortunately, it is known that for manifolds of dimension 4 and higher, no program exists that can decide whether two manifolds are diffeomorphic.
Smooth manifolds have a rich set of invariants, coming from point-set topology,
classic algebraic topologyAlgebraic topologyAlgebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, and geometric topologyGeometric topologyIn mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
. The most familiar invariants, which are visible for surfaces, are orientabilityOrientabilityIn mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
(a normal invariant, also detected by homologySingular homologyIn algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
) and genusGenus (mathematics)In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
(a homological invariant).
Smooth closed manifolds have no local invariants (other than dimension), though geometric manifolds have local invariants, notably the curvature of a Riemannian manifoldCurvature of Riemannian manifoldsIn mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension at least 3 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define it, now known as the curvature tensor...
and the torsion of a manifold equipped with an affine connectionAffine connectionIn the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
.
This distinction between no local invariants and local invariants is a common way to distinguish between geometry and topology. All invariants of a smooth closed manifold are thus global.
Algebraic topologyAlgebraic topologyAlgebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
is a source of a number of important global invariant properties. Some key criteria include the simply connected property and orientability (see below). Indeed several branches of mathematics, such as homologyHomology (mathematics)In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
and homotopyHomotopyIn topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
theory, and the theory of characteristic classes were founded in order to study invariant properties of manifolds.
Orientability
In dimensions two and higher, a simple but important invariant criterion is the question of whether a manifold admits a meaningful orientation.
Consider a topological manifold with charts mapping to Rn. Given an ordered basis for Rn, a chart causes its piece of the manifold to itself acquire a sense of ordering, which in 3-dimensions can be viewed as either right-handed or left-handed. Overlapping charts are not required to agree in their sense of ordering, which gives manifolds an important freedom. For some manifolds, like the sphere, charts can be chosen so that overlapping regions agree on their "handedness"; these are orientableOrientabilityIn mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
manifolds. For others, this is impossible. The latter possibility is easy to overlook, because any closed surface embedded (without self-intersection) in three-dimensional space is orientable.
Some illustrative examples of non-orientable manifolds include: (1) the Möbius stripMöbius stripThe Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
, which is a manifold with boundary, (2) the Klein bottleKlein bottleIn mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
, which must intersect itself in 3-space, and (3) the real projective planeReal projective planeIn mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
, which arises naturally in geometryGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
.
Möbius strip
Begin with an infinite circular cylinder standing vertically, a manifold without boundary. Slice across it high and low to produce two circular boundaries, and the cylindrical strip between them. This is an orientable manifold with boundary, upon which "surgery" will be performed. Slice the strip open, so that it could unroll to become a rectangle, but keep a grasp on the cut ends. Twist one end 180°, making the inner surface face out, and glue the ends back together seamlessly. This results in a strip with a permanent half-twist: the Möbius stripMöbius stripThe Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
. Its boundary is no longer a pair of circles, but (topologically) a single circle; and what was once its "inside" has merged with its "outside", so that it now has only a single side.
Klein bottle
Take two Möbius strips; each has a single loop as a boundary. Straighten out those loops into circles, and let the strips distort into cross-cap Cross-capIn mathematics, a cross-cap is a two-dimensional surface that is a model of a Möbius strip with a single self intersection. This self intersection precludes the cross-cap from being topologically equivalent to a Möbius strip...
Cross-capIn mathematics, a cross-cap is a two-dimensional surface that is a model of a Möbius strip with a single self intersection. This self intersection precludes the cross-cap from being topologically equivalent to a Möbius strip...
s. Gluing the circles together will produce a new, closed manifold without boundary, the Klein bottleKlein bottleIn mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
. Closing the surface does nothing to improve the lack of orientability, it merely removes the boundary. Thus, the Klein bottle is a closed surface with no distinction between inside and outside. Note that in three-dimensional space, a Klein bottle's surface must pass through itself. Building a Klein bottle which is not self-intersecting requires four or more dimensions of space.
Real projective plane
Begin with a sphere centered on the origin. Every line through the origin pierces the sphere in two opposite points called antipodes. Although there is no way to do so physically, it is possible to mathematically merge each antipode pair into a single point. The closed surface so produced is the real projective planeReal projective planeIn mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
, yet another non-orientable surface. It has a number of equivalent descriptions and constructions, but this route explains its name: all the points on any given line through the origin project to the same "point" on this "plane".
Genus and the Euler characteristic
For two dimensional manifolds a key invariant property is the genusGenus (mathematics)In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
, or the "number of handles" present in a surface. A torus is a sphere with one handle, a double torus is a sphere with two handles, and so on. Indeed it is possible to fully characterize compact, two-dimensional manifolds on the basis of genus and orientability. In higher-dimensional manifolds genus is replaced by the notion of Euler characteristicEuler characteristicIn mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
, and more generally Betti numbers and homologyHomology (mathematics)In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
and cohomologyCohomologyIn mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
.
Maps of manifolds
Just as there are various types of manifolds, there are various types of maps of manifoldsMaps of manifoldsIn mathematics, more specifically in differential geometry and topology, various types of functions between manifolds are studied, both as objects in their own right and for the light they shed- Types of maps :...
. In addition to continuous functions and smooth functions generally, there are maps with special properties. In geometric topologyGeometric topologyIn mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
a basic type are embeddingEmbeddingIn mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
s, of which knot theoryKnot theoryIn topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
is a central example, and generalizations such as immersions, submersionsSubmersion (mathematics)In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology...
, covering spaces, and ramified covering spaces.
Basic results include the Whitney embedding theorem and Whitney immersion theorem.
In Riemannian geometry, one may ask for maps to preserve the Riemannian metric, leading to notions of isometric embeddings, isometric immersions, and Riemannian submersionRiemannian submersionIn differential geometry, a branch of mathematics, a Riemannian submersion is a submersion from one Riemannian manifold to another that respects the metrics, meaning that it is an orthogonal projection on tangent spaces....
s; a basic result is the Nash embedding theoremNash embedding theoremThe Nash embedding theorems , named after John Forbes Nash, state that every Riemannian manifold can be isometrically embedded into some Euclidean space. Isometric means preserving the length of every path...
.
Scalar-valued functions
A basic example of maps between manifolds are scalar-valued functions on a manifold,
 or
or 
sometimes called regular functionRegular functionIn mathematics, a regular function is a function that is analytic and single-valued in a given region. In complex analysis, any complex regular function is known as a holomorphic function...
s or functionalFunctional (mathematics)In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
s, by analogy with algebraic geometry or linear algebra. These are of interest both in their own right, and to study the underlying manifold.
In geometric topology, most commonly studied are Morse functions, which yield handlebodyHandlebodyIn the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds...
decompositions, while in mathematical analysisMathematical analysisMathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, one often studies solution to partial differential equations, an important example of which is harmonic analysisHarmonic analysisHarmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, where one studies harmonic functionHarmonic functionIn mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s: the kernel of the Laplace operatorLaplace operatorIn mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
. This leads to such functions as the spherical harmonicsSpherical harmonicsIn mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
, and to heat kernelHeat kernelIn the mathematical study of heat conduction and diffusion, a heat kernel is the fundamental solution to the heat equation on a particular domain with appropriate boundary conditions. It is also one of the main tools in the study of the spectrum of the Laplace operator, and is thus of some...
methods of studying manifolds, such as hearing the shape of a drumHearing the shape of a drumTo hear the shape of a drum is to infer information about the shape of the drumhead from the sound it makes, i.e., from the list of basic harmonics, via the use of mathematical theory...
and some proofs of the Atiyah–Singer index theoremAtiyah–Singer index theoremIn differential geometry, the Atiyah–Singer index theorem, proved by , states that for an elliptic differential operator on a compact manifold, the analytical index is equal to the topological index...
.
Generalizations of manifolds
- Orbifolds: An orbifoldOrbifoldIn the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
is a generalization of manifold allowing for certain kinds of "singularitiesMathematical singularityIn mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
" in the topology. Roughly speaking, it is a space which locally looks like the quotients of some simple space (e.g. Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
) by the actionGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s of various finite groupFinite groupIn mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s. The singularities correspond to fixed points of the group actions, and the actions must be compatible in a certain sense.
- Algebraic varieties and schemes: Non-singular algebraic varieties over the real or complex numbers are manifolds. One generalizes this first by allowing singularities, secondly by allowing different fields, and thirdly by emulating the patching construction of manifolds: just as a manifold is glued together from open subsets of Euclidean space, an algebraic varietyAlgebraic varietyIn mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
is glued together from affine algebraic varieties, which are zero sets of polynomials over algebraically closed fields. SchemesScheme (mathematics)In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
are likewise glued together from affine schemes, which are a generalization of algebraic varieties. Both are related to manifolds, but are constructed algebraically using sheavesSheaf (mathematics)In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
instead of atlases.
- Because of singular pointMathematical singularityIn mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
s, a variety is in general not a manifold, though linguistically the French variété, German Mannigfaltigkeit and English manifold are largely synonymous. In French an algebraic variety is called une variété algébrique (an algebraic variety), while a smooth manifold is called une variété différentielle (a differential variety).
- CW-complexes: A CW complexCW complexIn topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
is a topological space formed by gluing disks of different dimensionality together. In general the resulting space is singular, and hence not a manifold. However, they are of central interest in algebraic topologyAlgebraic topologyAlgebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, especially in homotopy theory, as they are easy to compute with and singularities are not a concern.
See also
- List of manifolds
- SubmanifoldSubmanifoldIn mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
- Directional statistics: statistics on manifolds
By dimension
- CurveCurveIn mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
(1-manifold) - SurfaceSurfaceIn mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
(2-manifold) - 3-manifold3-manifoldIn mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
- 4-manifold4-manifoldIn mathematics, 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different...
- 5-manifold5-manifoldIn mathematics, a 5-manifold is a 5-dimensional topological manifold, possibly with a piecewise linear or smooth structure.Non-simply connected 5-manifolds are impossible to classify, as this is harder than solving the word problem for groups. Simply connected compact 5-manifolds were first...
External links
- Dimensions-math.org (A film explaining and visualizing manifolds up to fourth dimension.)
- The manifold atlas project of the Hausdorff Institute for Mathematics in Bonn
-





