
Compact space
Encyclopedia
In mathematics
, specifically general topology
and metric topology, a compact space is an abstract mathematical space
whose topology has the compactness property, which has many important implications not valid in general spaces. Compactness is not easy to describe precisely in an intuitive manner; in some sense it says that the topology allows the space to be considered as "small" (compactness is a kind of topological counterpart to finiteness of sets), even though as a set it may be quite large. Moreover, more intuitive characterizations of compactness are often dependent on additional properties of the topological space to be valid; the following description assumes the space is a metric space
, so that "closeness" of points has meaning. Then compactness means that whenever one chooses infinitely many sample points from the space, some of the samples must eventually get arbitrarily close to at least one point of the space. This could be because some point is itself sampled infinitely many times (as would necessarily happen if the space were finite), but a more significant possibility is that the point itself is not in the sample, but that any neighborhood of the point, however small, does contain infinitely many sample points.
Important, but non-obvious, examples of compact spaces are any closed interval
[a,b] of the real number
s, or any rectangle
(including its boundary) of the plane. More generally the Bolzano–Weierstrass theorem
characterizes compactness of subspaces of the real numbers, or more generally of finite dimensional Euclidean space
s, as those subsets that are both closed
and bounded. Apart from closed and bounded subsets of Euclidean space, typical examples of compact spaces include spaces consisting not of geometrical points but of functions
. The term compact was introduced into mathematics by Maurice Fréchet in 1906 as a distillation of this concept. Compactness in this more general situation plays an extremely important role in mathematical analysis
, because many classical and important theorems of 19th century analysis, such as the extreme value theorem
, are easily generalized to this situation. A typical application is furnished by the Arzelà–Ascoli theorem and in particular the Peano existence theorem
, in which one is able to conclude the existence of a function with some required properties as a limiting case of some more elementary construction.
There are several different notions of compactness, noted below, that are equivalent in some settings; the version described above is known as sequential compactness. In general metric space
s various notions of compactness, including sequential compactness and limit point compact
ness are equivalent. In general topological space
s, however, the different notions of compactness are not necessarily equivalent, and the most useful notion, introduced by Pavel Alexandrov and Pavel Urysohn in 1929, involves the existence of certain finite families of open set
s that cover
the space in the sense that each point of the space must lie in some set contained in the family. This more subtle definition exhibits compact spaces as generalizations of finite sets. In spaces that are compact in this latter sense, it is often possible to patch together information that holds locally
(that is, in a neighborhood of each point) into corresponding statements that hold throughout the space, and many theorems are of this character.
[0,1] of real numbers. If one chooses an infinite number of distinct points in the unit interval, then there must be some accumulation point in that interval. For instance, the odd terms of the sequence get arbitrarily close to 0, while the even ones get arbitrarily close to 1. If one would choose the sequence of points at random
, then any point of the interval would ultimately be approached arbitrarily closely by some of the chosen points. The given example sequence shows the importance of including the boundary points of the interval, since the limit points must be in the space itself: an open (or half-open) interval of the real numbers is not compact. It is also crucial that the interval be bounded
, since in the interval [0,∞) one could choose the sequence of points , of which no sub-sequence ultimately gets arbitrarily close to any given real number.
In two dimensions, closed disks
are compact since for any infinite number of points sampled from a disk, some subset of those points must get arbitrarily close either to a point within the disc, or to a point on the boundary. However, an open disk is not compact, because a sequence of points can tend to the boundary without getting arbitrarily close to any point in the interior. Likewise, spheres are compact, but a sphere missing a point is not since a sequence of points can tend to the missing point without tending to any point within the space. Lines and planes are not compact, since one can take a set of equally spaced points in any given direction without approaching any point.
Compactness generalizes many important properties of closed and bounded intervals in the real line; that is, intervals of the form [a,b] for real numbers a and b. For instance, any continuous function defined on a compact space into an ordered set (with the order topology
) such as the real line is bounded. Thus, what is known as the extreme value theorem
in calculus
generalizes to compact spaces. In this fashion, one can prove many important theorems in the class of compact spaces, that do not hold in the context of non-compact ones.
Various definitions of compactness may apply, depending on the level of generality. A subset of Euclidean space
in particular is called compact if it is closed
and bounded
. This implies, by the Bolzano–Weierstrass theorem
, that any infinite sequence from the set has a subsequence
that converges to a point in the set. This puts a fine point on the idea of taking "steps" in a space. Various equivalent notions of compactness, such as sequential compactness and limit point compact
ness, can be developed in general metric space
s.
In general topological space
s, however, the different notions of compactness are not equivalent, and the most useful notion of compactness—originally called bicompactness—involves families of open set
s that "cover" the space in the sense that each point of the space must lie in some set contained in the family. Specifically, a topological space is compact if, whenever a collection of open sets covers the space, some subcollection consisting only of finitely many open sets also covers the space. That this form of compactness holds for closed and bounded subsets of Euclidean space is known as the Heine–Borel theorem
. Compactness, when defined in this manner, often allows one to take information that is known locally
—in a neighborhood of each point of the space—and to extend it to information that holds globally throughout the space. An example of this phenomenon is Dirichlet's theorem, to which it was originally applied by Heine, that a continuous function
on a compact interval is uniformly continuous: here continuity is a local property of the function, and uniform continuity the corresponding global property.
X is called compact if each of its open covers has a finite subcover. Otherwise it is called non-compact. Explicitly, this means that for every arbitrary collection
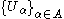
of open subsets of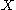 such that
such that

there is a finite subset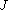 of
of 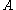 such that
such that
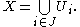
Some branches of mathematics such as algebraic geometry
, typically influenced by the French school of Bourbaki
, use the term quasi-compact for the general notion, and reserve the term compact for topological spaces that are both Hausdorff and quasi-compact. A single compact set is sometimes referred to as a compactum; following the Latin
second declension (neuter), the corresponding plural form is compacta.
. Explicitly, this means that for every arbitrary collection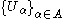
of open subsets of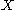 such that
such that
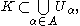
there is a finite subset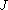 of
of 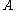 such that
such that

(1817) had been aware that any bounded sequence of points (in the line or plane, for instance) has a subsequence that must eventually get arbitrarily close to some other point, called a limit point
. Bolzano's proof relied on the method of bisection: the sequence was placed into an interval that was then divided into two equal parts, and a part containing infinitely many terms of the sequence was selected. The process could then be repeated by dividing the resulting smaller interval into smaller and smaller parts until it closes down on the desired limit point. The full significance of Bolzano's theorem, and its method of proof, would not emerge until almost 50 years later when it was rediscovered by Karl Weierstrass
.
In the 1880s, it became clear that results similar to the Bolzano–Weierstrass theorem could be formulated for spaces of functions rather than just numbers or geometrical points. The idea of regarding functions as themselves points of a generalized space dates back to the investigations of Giulio Ascoli
and Cesare Arzelà
. The culmination of their investigations, the Arzelà–Ascoli theorem, was a generalization of the Bolzano–Weierstrass theorem to families of continuous function
s, the precise conclusion of which was that it was possible to extract a uniformly convergent sequence of functions from a suitable family of functions. The uniform limit of this sequence then played precisely the same role as Bolzano's "limit point". Towards the beginning of the twentieth century, results similar to that of Arzelà and Ascoli began to accumulate in the area of integral equation
s, as investigated by David Hilbert
and Erhard Schmidt
. For a certain class of Green function
s coming from solutions of integral equations, Schmidt had shown that a property analogous to the Arzelà–Ascoli theorem held in the sense of mean convergence—or convergence in what would later be dubbed a Hilbert space
. This ultimately led to the notion of a compact operator
as an offshoot of the general notion of a compact space. It was Maurice Fréchet
who, in 1906, had distilled the essence of the Bolzano–Weierstrass property and coined the term compactness to refer to this general phenomenon.
However, a different notion of compactness altogether had also slowly emerged at the turn of the century from the study of the continuum
, which was seen as fundamental for the rigorous formulation of analysis. In 1870, Eduard Heine
showed that a continuous function
defined on a closed and bounded interval was in fact uniformly continuous. In the course of the proof, he made use of a lemma that from any countable cover of the interval by smaller open intervals, it was possible to select a finite number of these that also covered it. The significance of this lemma was recognized by Émile Borel
(1895), and it was generalized to arbitrary collections of intervals by Pierre Cousin (1895) and Henri Lebesgue
(1904). The Heine–Borel theorem
, as the result is now known, is another special property possessed by closed and bounded sets of real numbers.
This property was significant because it allowed for the passage from local information
about a set (such as the continuity of a function) to global information about the set (such as the uniform continuity of a function). This sentiment was expressed by , who also exploited it in the development of the integral now bearing his name. Ultimately the Russian school of point-set topology, under the direction of Pavel Alexandrov and Pavel Urysohn, formulated Heine–Borel compactness in a way that could be applied to the modern notion of a topological space
. showed that the earlier version of compactness due to Fréchet, now called (relative) sequential compactness, under appropriate conditions followed from the version of compactness that was formulated in terms of the existence of finite subcovers. It was this notion of compactness that became the dominant one, because it was not only a stronger property, but it could be formulated in a more general setting with a minimum of additional technical machinery, as it relied only on the structure of the open sets in a space.
Characterizations of compactness
The following are equivalent.
Euclidean space
For any subset
A of Euclidean space
Rn, the following are equivalent:
In practice, the condition (5) is easiest to verify, for example a closed interval
or closed n-ball. Note that, in a metric space, every compact subset is closed and bounded. However, the converse may fail in non-Euclidean Rn. For example, the real line
equipped with the discrete topology is closed and bounded but not compact, as the collection of all singleton points of the space is an open cover which admits no finite subcover.
Metric spaces
Hausdorff spaces
While all these conditions are equivalent for metric space
s, in general we have the following implications:
Not every countably compact space is compact; an example is given by the first uncountable ordinal
with the order topology
.
Not every compact space is sequentially compact; an example is given by 2[0,1], with the product topology .
A metric space is called pre-compact or totally bounded if any sequence has a Cauchy subsequence; this can be generalised to uniform space
s. For complete metric spaces this is equivalent to compactness. See relatively compact for the topological version.
Another related notion which (by most definitions) is strictly weaker than compactness is local compactness
.
Generalizations of compactness include H-closed and the property of being an H-set in a parent space. A space is
H-closed if every open cover has a finite subfamily whose union is dense. Whereas we say X is an H-set of Z if
every cover of X with open sets of Z has a finite subfamily whose Z closure contains X.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically general topology
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
and metric topology, a compact space is an abstract mathematical space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
whose topology has the compactness property, which has many important implications not valid in general spaces. Compactness is not easy to describe precisely in an intuitive manner; in some sense it says that the topology allows the space to be considered as "small" (compactness is a kind of topological counterpart to finiteness of sets), even though as a set it may be quite large. Moreover, more intuitive characterizations of compactness are often dependent on additional properties of the topological space to be valid; the following description assumes the space is a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, so that "closeness" of points has meaning. Then compactness means that whenever one chooses infinitely many sample points from the space, some of the samples must eventually get arbitrarily close to at least one point of the space. This could be because some point is itself sampled infinitely many times (as would necessarily happen if the space were finite), but a more significant possibility is that the point itself is not in the sample, but that any neighborhood of the point, however small, does contain infinitely many sample points.
Important, but non-obvious, examples of compact spaces are any closed interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[a,b] of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, or any rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
(including its boundary) of the plane. More generally the Bolzano–Weierstrass theorem
Bolzano–Weierstrass theorem
In real analysis, the Bolzano–Weierstrass theorem is a fundamental result about convergence in a finite-dimensional Euclidean space Rn. The theorem states thateach bounded sequence in Rn has a convergent subsequence...
characterizes compactness of subspaces of the real numbers, or more generally of finite dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s, as those subsets that are both closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and bounded. Apart from closed and bounded subsets of Euclidean space, typical examples of compact spaces include spaces consisting not of geometrical points but of functions
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
. The term compact was introduced into mathematics by Maurice Fréchet in 1906 as a distillation of this concept. Compactness in this more general situation plays an extremely important role in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, because many classical and important theorems of 19th century analysis, such as the extreme value theorem
Extreme value theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
, are easily generalized to this situation. A typical application is furnished by the Arzelà–Ascoli theorem and in particular the Peano existence theorem
Peano existence theorem
In mathematics, specifically in the study of ordinary differential equations, the Peano existence theorem, Peano theorem or Cauchy-Peano theorem, named after Giuseppe Peano and Augustin Louis Cauchy, is a fundamental theorem which guarantees the existence of solutions to certain initial value...
, in which one is able to conclude the existence of a function with some required properties as a limiting case of some more elementary construction.
There are several different notions of compactness, noted below, that are equivalent in some settings; the version described above is known as sequential compactness. In general metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s various notions of compactness, including sequential compactness and limit point compact
Limit point compact
In mathematics, a topological space X is said to be limit point compact or weakly countably compact if every infinite subset of X has a limit point in X. This property generalizes a property of compact spaces. In a metric space, limit point compactness, compactness, and sequential compactness are...
ness are equivalent. In general topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, however, the different notions of compactness are not necessarily equivalent, and the most useful notion, introduced by Pavel Alexandrov and Pavel Urysohn in 1929, involves the existence of certain finite families of open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s that cover
Cover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
the space in the sense that each point of the space must lie in some set contained in the family. This more subtle definition exhibits compact spaces as generalizations of finite sets. In spaces that are compact in this latter sense, it is often possible to patch together information that holds locally
Local property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
(that is, in a neighborhood of each point) into corresponding statements that hold throughout the space, and many theorems are of this character.
Introduction
An example of a compact space is the unit intervalUnit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0,1] of real numbers. If one chooses an infinite number of distinct points in the unit interval, then there must be some accumulation point in that interval. For instance, the odd terms of the sequence get arbitrarily close to 0, while the even ones get arbitrarily close to 1. If one would choose the sequence of points at random
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, then any point of the interval would ultimately be approached arbitrarily closely by some of the chosen points. The given example sequence shows the importance of including the boundary points of the interval, since the limit points must be in the space itself: an open (or half-open) interval of the real numbers is not compact. It is also crucial that the interval be bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
, since in the interval [0,∞) one could choose the sequence of points , of which no sub-sequence ultimately gets arbitrarily close to any given real number.
In two dimensions, closed disks
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
are compact since for any infinite number of points sampled from a disk, some subset of those points must get arbitrarily close either to a point within the disc, or to a point on the boundary. However, an open disk is not compact, because a sequence of points can tend to the boundary without getting arbitrarily close to any point in the interior. Likewise, spheres are compact, but a sphere missing a point is not since a sequence of points can tend to the missing point without tending to any point within the space. Lines and planes are not compact, since one can take a set of equally spaced points in any given direction without approaching any point.
Compactness generalizes many important properties of closed and bounded intervals in the real line; that is, intervals of the form [a,b] for real numbers a and b. For instance, any continuous function defined on a compact space into an ordered set (with the order topology
Order topology
In mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
) such as the real line is bounded. Thus, what is known as the extreme value theorem
Extreme value theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
in calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
generalizes to compact spaces. In this fashion, one can prove many important theorems in the class of compact spaces, that do not hold in the context of non-compact ones.
Various definitions of compactness may apply, depending on the level of generality. A subset of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
in particular is called compact if it is closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
. This implies, by the Bolzano–Weierstrass theorem
Bolzano–Weierstrass theorem
In real analysis, the Bolzano–Weierstrass theorem is a fundamental result about convergence in a finite-dimensional Euclidean space Rn. The theorem states thateach bounded sequence in Rn has a convergent subsequence...
, that any infinite sequence from the set has a subsequence
Subsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
that converges to a point in the set. This puts a fine point on the idea of taking "steps" in a space. Various equivalent notions of compactness, such as sequential compactness and limit point compact
Limit point compact
In mathematics, a topological space X is said to be limit point compact or weakly countably compact if every infinite subset of X has a limit point in X. This property generalizes a property of compact spaces. In a metric space, limit point compactness, compactness, and sequential compactness are...
ness, can be developed in general metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s.
In general topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, however, the different notions of compactness are not equivalent, and the most useful notion of compactness—originally called bicompactness—involves families of open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s that "cover" the space in the sense that each point of the space must lie in some set contained in the family. Specifically, a topological space is compact if, whenever a collection of open sets covers the space, some subcollection consisting only of finitely many open sets also covers the space. That this form of compactness holds for closed and bounded subsets of Euclidean space is known as the Heine–Borel theorem
Heine–Borel theorem
In the topology of metric spaces the Heine–Borel theorem, named after Eduard Heine and Émile Borel, states:For a subset S of Euclidean space Rn, the following two statements are equivalent:*S is closed and bounded...
. Compactness, when defined in this manner, often allows one to take information that is known locally
Local property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
—in a neighborhood of each point of the space—and to extend it to information that holds globally throughout the space. An example of this phenomenon is Dirichlet's theorem, to which it was originally applied by Heine, that a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on a compact interval is uniformly continuous: here continuity is a local property of the function, and uniform continuity the corresponding global property.
Definition
Formally, a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is called compact if each of its open covers has a finite subcover. Otherwise it is called non-compact. Explicitly, this means that for every arbitrary collection
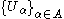
of open subsets of
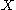 such that
such that
there is a finite subset
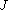 of
of 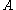 such that
such that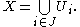
Some branches of mathematics such as algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, typically influenced by the French school of Bourbaki
Nicolas Bourbaki
Nicolas Bourbaki is the collective pseudonym under which a group of 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality...
, use the term quasi-compact for the general notion, and reserve the term compact for topological spaces that are both Hausdorff and quasi-compact. A single compact set is sometimes referred to as a compactum; following the Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
second declension (neuter), the corresponding plural form is compacta.
Compactness of subspaces
A subset K of a topological space X is called compact if it is compact in the induced topologyInduced topology
In topology and related areas of mathematics, an induced topology on a topological space is a topology which is "optimal" for some function from/to this topological space.- Definition :Let X_0, X_1 be sets, f:X_0\to X_1....
. Explicitly, this means that for every arbitrary collection
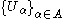
of open subsets of
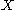 such that
such that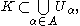
there is a finite subset
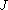 of
of 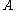 such that
such that
Historical development
In the 19th century, several disparate mathematical properties were understood that would later be seen as consequences of compactness. On the one hand, Bernard BolzanoBernard Bolzano
Bernhard Placidus Johann Nepomuk Bolzano , Bernard Bolzano in English, was a Bohemian mathematician, logician, philosopher, theologian, Catholic priest and antimilitarist of German mother tongue.-Family:Bolzano was the son of two pious Catholics...
(1817) had been aware that any bounded sequence of points (in the line or plane, for instance) has a subsequence that must eventually get arbitrarily close to some other point, called a limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
. Bolzano's proof relied on the method of bisection: the sequence was placed into an interval that was then divided into two equal parts, and a part containing infinitely many terms of the sequence was selected. The process could then be repeated by dividing the resulting smaller interval into smaller and smaller parts until it closes down on the desired limit point. The full significance of Bolzano's theorem, and its method of proof, would not emerge until almost 50 years later when it was rediscovered by Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
.
In the 1880s, it became clear that results similar to the Bolzano–Weierstrass theorem could be formulated for spaces of functions rather than just numbers or geometrical points. The idea of regarding functions as themselves points of a generalized space dates back to the investigations of Giulio Ascoli
Giulio Ascoli
Giulio Ascoli was an Italian mathematician. He was a student of the Scuola Normale di Pisa, where he graduated in 1868.In 1872 he became Professor of Algebra and Calculus of the Politecnico di Milano University...
and Cesare Arzelà
Cesare Arzelà
Cesare Arzelà was an Italian mathematician who taught at the University of Bologna and is recognized for his contributions in the theory of functions, particularly for his characterization of sequences of continuous functions, generalizing the one given earlier by Giulio Ascoli in the famous...
. The culmination of their investigations, the Arzelà–Ascoli theorem, was a generalization of the Bolzano–Weierstrass theorem to families of continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s, the precise conclusion of which was that it was possible to extract a uniformly convergent sequence of functions from a suitable family of functions. The uniform limit of this sequence then played precisely the same role as Bolzano's "limit point". Towards the beginning of the twentieth century, results similar to that of Arzelà and Ascoli began to accumulate in the area of integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
s, as investigated by David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
and Erhard Schmidt
Erhard Schmidt
Erhard Schmidt was a German mathematician whose work significantly influenced the direction of mathematics in the twentieth century. He was born in Tartu, Governorate of Livonia . His advisor was David Hilbert and he was awarded his doctorate from Georg-August University of Göttingen in 1905...
. For a certain class of Green function
Green function
Green function might refer to:*Green's function of a differential operator.*Deligne–Lusztig theory in the representation theory of finite groups of Lie type.*Green's function in many-body theory....
s coming from solutions of integral equations, Schmidt had shown that a property analogous to the Arzelà–Ascoli theorem held in the sense of mean convergence—or convergence in what would later be dubbed a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. This ultimately led to the notion of a compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
as an offshoot of the general notion of a compact space. It was Maurice Fréchet
Maurice René Fréchet
Maurice Fréchet was a French mathematician. He made major contributions to the topology of point sets and introduced the entire concept of metric spaces. He also made several important contributions to the field of statistics and probability, as well as calculus...
who, in 1906, had distilled the essence of the Bolzano–Weierstrass property and coined the term compactness to refer to this general phenomenon.
However, a different notion of compactness altogether had also slowly emerged at the turn of the century from the study of the continuum
Linear continuum
In the mathematical field of order theory, a continuum or linear continuum is a generalization of the real line.Formally, a linear continuum is a linearly ordered set S of more than one element that is densely ordered, i.e., between any two members there is another, and which "lacks gaps" in the...
, which was seen as fundamental for the rigorous formulation of analysis. In 1870, Eduard Heine
Eduard Heine
Heinrich Eduard Heine was a German mathematician.Heine became known for results on special functions and in real analysis. In particular, he authored an important treatise on spherical harmonics and Legendre functions . He also investigated basic hypergeometric series...
showed that a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
defined on a closed and bounded interval was in fact uniformly continuous. In the course of the proof, he made use of a lemma that from any countable cover of the interval by smaller open intervals, it was possible to select a finite number of these that also covered it. The significance of this lemma was recognized by Émile Borel
Émile Borel
Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
(1895), and it was generalized to arbitrary collections of intervals by Pierre Cousin (1895) and Henri Lebesgue
Henri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
(1904). The Heine–Borel theorem
Heine–Borel theorem
In the topology of metric spaces the Heine–Borel theorem, named after Eduard Heine and Émile Borel, states:For a subset S of Euclidean space Rn, the following two statements are equivalent:*S is closed and bounded...
, as the result is now known, is another special property possessed by closed and bounded sets of real numbers.
This property was significant because it allowed for the passage from local information
Local property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
about a set (such as the continuity of a function) to global information about the set (such as the uniform continuity of a function). This sentiment was expressed by , who also exploited it in the development of the integral now bearing his name. Ultimately the Russian school of point-set topology, under the direction of Pavel Alexandrov and Pavel Urysohn, formulated Heine–Borel compactness in a way that could be applied to the modern notion of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. showed that the earlier version of compactness due to Fréchet, now called (relative) sequential compactness, under appropriate conditions followed from the version of compactness that was formulated in terms of the existence of finite subcovers. It was this notion of compactness that became the dominant one, because it was not only a stronger property, but it could be formulated in a more general setting with a minimum of additional technical machinery, as it relied only on the structure of the open sets in a space.
General topology
- Any finite topological spaceFinite topological spaceIn mathematics, a finite topological space is a topological space for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points....
, including the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, is compact. Slightly more generally, any space with a finite topology (only finitely many open sets) is compact; this includes in particular the trivial topologyTrivial topologyIn topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
. - Any space carrying the cofinite topology is compact.
- Any locally compact Hausdorff space can be turned into a compact space by adding a single point to it, by means of Alexandroff one-point compactification. The one-point compactification of R is homeomorphic to the circle
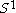 ; the one-point compactification of R2 is homeomorphic to the sphere
; the one-point compactification of R2 is homeomorphic to the sphere 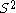 . Using the one-point compactification, one can also easily construct compact spaces which are not Hausdorff, by starting with a non-Hausdorff space.
. Using the one-point compactification, one can also easily construct compact spaces which are not Hausdorff, by starting with a non-Hausdorff space. - The right order topology or left order topology on any bounded totally ordered set is compact. In particular, Sierpinski spaceSierpinski spaceIn mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed.It is the smallest example of a topological space which is neither trivial nor discrete...
is compact. - R carrying the lower limit topologyLower limit topologyIn mathematics, the lower limit topology or right half-open interval topology is a topology defined on the set R of real numbers; it is different from the standard topology on R and has a number of interesting properties...
satisfies the property that no uncountable set is compact. - In the cocountable topologyCocountable topologyThe cocountable topology or countable complement topology on any set X consists of the empty set and all cocountable subsets of X, that is all sets whose complement in X is countable...
on R (or any uncountable set for that matter), no infinite set is compact. - Neither of the spaces in the previous two examples are locally compact but both are still LindelöfLindelöf spaceIn mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
Analysis and algebra
- The closed unit intervalUnit intervalIn mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0, 1] is compact. This follows from the Heine–Borel theoremHeine–Borel theoremIn the topology of metric spaces the Heine–Borel theorem, named after Eduard Heine and Émile Borel, states:For a subset S of Euclidean space Rn, the following two statements are equivalent:*S is closed and bounded...
. The open interval (0, 1) is not compact: the open cover ( 1/n, 1−1/n ) for n = 3, 4, … does not have a finite subcover. Similarly, the set of rational numbers in the closed interval [0, 1] is not compact: the sets of rational numbers in the intervals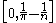 and
and  cover all the rationals in [0, 1] for n = 4, 5, … but this cover does not have a finite subcover. (Note that the sets are open in the subspace topology even though they are not open as subsets of R.)
cover all the rationals in [0, 1] for n = 4, 5, … but this cover does not have a finite subcover. (Note that the sets are open in the subspace topology even though they are not open as subsets of R.) - The set R of all real numbers is not compact as there is a cover of open intervals that does not have a finite subcover. For example, intervals , where n takes all integer values in Z, cover R but there is no finite subcover.
- More generally, compact groupCompact groupIn mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
s such as an orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
are compact, while groups such as a general linear groupGeneral linear groupIn mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
are not. - For every natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n, the n-sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
is compact. Again from the Heine–Borel theorem, the closed unit ball of any finite-dimensional normed vector spaceNormed vector spaceIn mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
is compact. This is not true for infinite dimensions; in fact, a normed vector space is finite-dimensional if and only if its closed unit ball is compact. - On the other hand, the closed unit ball of the dual of a normed space is compact for the weak-* topology. (Alaoglu's theorem)
- The Cantor setCantor setIn mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
is compact. In fact, every compact metric space is a continuous image of the Cantor set. - Since the p-adic integers are homeomorphic to the Cantor set, they form a compact set.
- Consider the set
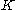 of all functions
of all functions 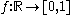 from the real number line to the closed unit interval, and define a topology on
from the real number line to the closed unit interval, and define a topology on  so that a sequence
so that a sequence  in
in  converges towards
converges towards 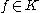 if and only if
if and only if 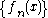 converges towards
converges towards  for all
for all 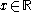 . There is only one such topology; it is called the topology of pointwise convergence. Then
. There is only one such topology; it is called the topology of pointwise convergence. Then 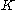 is a compact topological space; this follows from the Tychonoff theorem.
is a compact topological space; this follows from the Tychonoff theorem. - Consider the set K of all functions ƒ : [0, 1] → [0, 1] satisfying the Lipschitz condition |ƒ(x) − ƒ(y)| ≤ |x − y| for all x, y ∈ [0, 1]. Consider on K the metric induced by the uniform distance
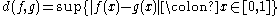 . Then by Arzelà–Ascoli theorem the space K is compact.
. Then by Arzelà–Ascoli theorem the space K is compact. - The spectrum of any bounded linear operator on a Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
is a nonempty compact subset of the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C. Conversely, any compact subset of C arises in this manner, as the spectrum of some bounded linear operator. For instance, a diagonal operator on the Hilbert space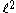 may have any compact nonempty subset of C as spectrum.
may have any compact nonempty subset of C as spectrum. - The spectrumSpectrum of a ringIn abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
of any commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
with the Zariski topologyZariski topologyIn algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
(that is, the set of all prime ideals) is compact, but never HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
(except in trivial cases). In algebraic geometry, such topological spaces are examples of quasi-compact schemesScheme (mathematics)In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
, "quasi" referring to the non-Hausdorff nature of the topology. - The spectrum of a Boolean algebra is compact, a fact which is part of the Stone representation theorem. Stone spaces, compact totally disconnectedTotally disconnected spaceIn topology and related branches of mathematics, a totally disconnected space is a topological space that is maximally disconnected, in the sense that it has no non-trivial connected subsets...
Hausdorff spaces, form the abstract framework in which these spectra are studied. Such spaces are also useful in the study of profinite groups. - The structure spaceStructure spaceThe structure space of a commutative Banach algebra is an analog of the spectrum of a C*-algebra. It consists of all multiplicative linear functionals on the algebra. The Gelfand representation of the Banach algebra is a map taking the Banach algebra elements to continuous functions on the...
of a commutative unital Banach algebraBanach algebraIn mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
is a compact Hausdorff space. - The Hilbert cubeHilbert cubeIn mathematics, the Hilbert cube, named after David Hilbert, is a topological space that provides an instructive example of some ideas in topology...
is compact, again a consequence of Tychonoff's theorem.
Theorems
Some theorems related to compactness (see the glossary of topology for the definitions):- A continuous image of a compact space is compact.
- The pre-image of a compact space under a proper mapProper mapIn mathematics, a continuous function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism.- Definition :...
is compact. - The extreme value theoremExtreme value theoremIn calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
: a continuous real-valued function on a nonempty compact space is bounded above and attains its supremum. (Slightly more generally, this is true for an upper semicontinuous function.) - A closed subset of a compact space is compact.
- A finite union of compact sets is compact.
- A nonempty compact subset of the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s has a greatest element and a least element. - The productProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of any collection of compact spaces is compact. (Tychonoff's theoremTychonoff's theoremIn mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact. The theorem is named after Andrey Nikolayevich Tychonoff, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the...
, which is equivalent to the axiom of choice) - Every topological space X is a dense subspace of a compact space having at most one point more than X, by the Alexandroff one-point compactificationCompactification (mathematics)In mathematics, compactification is the process or result of making a topological space compact. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".-An...
. By the same construction, every locally compact Hausdorff space X is a dense subspace of a compact Hausdorff space having at most one point more than X.. - Let X be a simply orderedTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
set endowed with the order topologyOrder topologyIn mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
. Then X is compact if and only if X is a complete latticeComplete latticeIn mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
(i.e. all subsets have suprema and infima).
Characterizations of compactness
The following are equivalent.
- A topological space X is compact.
- Any collection of closed subsets of X with the finite intersection propertyFinite intersection propertyIn general topology, a branch of mathematics, the finite intersection property is a property of a collection of subsets of a set X. A collection has this property if the intersection over any finite subcollection of the collection is nonempty....
has nonempty intersection. - X has a sub-base such that every cover of the space by members of the sub-base has a finite subcover (Alexander's sub-base theorem)
- Every netNet (mathematics)In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
on X has a convergent subnet (see the article on netsNet (mathematics)In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
for a proof). - Every filter on X has a convergent refinement.
- Every ultrafilterUltrafilterIn the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
on X converges to at least one point. - Every infinite subset of X has a complete accumulation point.
Euclidean space
For any subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
A of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, the following are equivalent:
- A is compact.
- Every open cover of A has a finite subcover.
- Every sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
in A has a convergentLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
subsequence, whose limit lies in A. - Every infinite subset of A has at least one limit pointLimit pointIn mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
in A. - A is closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and boundedBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
(Heine-Borel theorem). - A is complete and totally bounded.
In practice, the condition (5) is easiest to verify, for example a closed interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
or closed n-ball. Note that, in a metric space, every compact subset is closed and bounded. However, the converse may fail in non-Euclidean Rn. For example, the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
equipped with the discrete topology is closed and bounded but not compact, as the collection of all singleton points of the space is an open cover which admits no finite subcover.
Metric spaces
- A metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
(or uniform spaceUniform spaceIn the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
) is compact if and only if it is complete and totally bounded. - If the metric space X is compact and an open cover of X is given, then there exists a number δ > 0 such that every subset of X of diameter < δ is contained in some member of the cover. (Lebesgue's number lemmaLebesgue's number lemmaIn topology, Lebesgue's number lemma, named after Henri Lebesgue, is a useful tool in the study of compact metric spaces. It states:Such a number δ is called a Lebesgue number of this cover. The notion of a Lebesgue number itself is useful in other applications as well.-References:-External links:*...
) - Every compact metric space is separable.
- A metric space (or more generally any first-countable uniform spaceUniform spaceIn the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
) is compact if and only if every sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
in the space has a convergent subsequence. (Sequentially compact)
Hausdorff spaces
- A compact subset of a Hausdorff space is closed. More generally, compact sets can be separated by open sets: if K1 and K2 are compact and disjoint, there exist disjoint open sets U1 and U2 such that
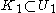 and
and 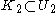 . This is to say, compact Hausdorff space is normalNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
. This is to say, compact Hausdorff space is normalNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
. - Two compact Hausdorff spaces X1 and X2 are homeomorphic if and only if their rings of continuous real-valued functions C(X1) and C(X2) are isomorphicRing homomorphismIn ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
. (Gelfand–Naimark theoremGelfand–Naimark theoremIn mathematics, the Gelfand–Naimark theorem states that an arbitrary C*-algebra A is isometrically *-isomorphic to a C*-algebra of bounded operators on a Hilbert space...
) Properties of the Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
of continuous functions on a compact Hausdorff spaceContinuous functions on a compact Hausdorff spaceIn mathematical analysis, and especially functional analysis, a fundamental role is played by the space of continuous functions on a compact Hausdorff space with values in the real or complex numbers. This space, denoted by C, is a vector space with respect to the pointwise addition of functions...
are central to abstract analysis. - Every continuous map from a compact space to a Hausdorff space is closed and properProper mapIn mathematics, a continuous function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism.- Definition :...
(i.e., the pre-image of a compact set is compact.) In particular, every continuous bijective map from a compact space to a Hausdorff space is a homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
. - A topological space can be embedded in a compact Hausdorff space if and only if it is a Tychonoff spaceTychonoff spaceIn topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
.
Other forms of compactness
There are a number of topological properties which are equivalent to compactness in metric spaces, but are inequivalent in general topological spaces. These include the following.- Sequentially compactSequentially compact spaceIn mathematics, a topological space is sequentially compact if every sequence has a convergent subsequence. For general topological spaces, the notions of compactness and sequential compactness are not equivalent; they are, however, equivalent for metric spaces....
: Every sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
has a convergent subsequence. - Countably compactCountably compact spaceIn mathematics a topological space is countably compact if every countable open cover has a finite subcover.-Examples and Properties:A compact space is countably compact...
: Every countable open cover has a finite subcover. (Or, equivalently, every infinite subset has an ω-accumulation point.) - PseudocompactPseudocompact spaceIn mathematics, in the field of topology, a topological space is said to be pseudocompact if its image under any continuous function to R is bounded.-Properties related to pseudocompactness:...
: Every real-valued continuous functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on the space is bounded. - Limit point compactLimit point compactIn mathematics, a topological space X is said to be limit point compact or weakly countably compact if every infinite subset of X has a limit point in X. This property generalizes a property of compact spaces. In a metric space, limit point compactness, compactness, and sequential compactness are...
: Every infinite subset has an accumulation point.
While all these conditions are equivalent for metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s, in general we have the following implications:
- Compact spaces are countably compact.
- Sequentially compact spaces are countably compact.
- Countably compact spaces are pseudocompact and weakly countably compact.
Not every countably compact space is compact; an example is given by the first uncountable ordinal
First uncountable ordinal
In mathematics, the first uncountable ordinal, traditionally denoted by ω1 or sometimes by Ω, is the smallest ordinal number that, considered as a set, is uncountable. It is the supremum of all countable ordinals...
with the order topology
Order topology
In mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
.
Not every compact space is sequentially compact; an example is given by 2[0,1], with the product topology .
A metric space is called pre-compact or totally bounded if any sequence has a Cauchy subsequence; this can be generalised to uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
s. For complete metric spaces this is equivalent to compactness. See relatively compact for the topological version.
Another related notion which (by most definitions) is strictly weaker than compactness is local compactness
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
.
Generalizations of compactness include H-closed and the property of being an H-set in a parent space. A space is
H-closed if every open cover has a finite subfamily whose union is dense. Whereas we say X is an H-set of Z if
every cover of X with open sets of Z has a finite subfamily whose Z closure contains X.
See also
- Compactly generated spaceCompactly generated spaceIn topology, a compactly generated space is a topological space whose topology is coherent with the family of all compact subspaces. Specifically, a topological space X is compactly generated if it satisfies the following condition:Equivalently, one can replace closed with open in this definition...
- Exhaustion by compact sets
- Lindelöf spaceLindelöf spaceIn mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
- Metacompact spaceMetacompact spaceIn mathematics, in the field of general topology, a topological space is said to be metacompact if every open cover has a point finite open refinement...
- Noetherian space
- Orthocompact spaceOrthocompact spaceIn mathematics, in the field of general topology, a topological space is said to be orthocompact if every open cover has an interior preserving open refinement...
- Paracompact spaceParacompact spaceIn mathematics, a paracompact space is a topological space in which every open cover admits a locally finite open refinement. Paracompact spaces are sometimes also required to be Hausdorff. Paracompact spaces were introduced by ....

