
CW complex
Encyclopedia
In topology
, a CW complex is a type of topological space
introduced by J. H. C. Whitehead
to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical
properties than simplicial complex
es, but still retains a combinatorial nature
that allows for computation.
An n-dimensional closed cell is a topological space that is homeomorphic to an n-dimensional closed ball. For example, a simplex
is a closed cell, and more generally, a convex polytope
is a closed cell. An n-dimensional open cell is a topological space that is homeomorphic to the open ball. A 0-dimensional open (and closed) cell is a singleton space.
A CW complex is a Hausdorff space
X together with a partition
of X into open cells (of varying dimension) that satisfies two additional properties:
of a CW complex is the union of the cells whose dimension is at most n. If the union of a set of cells is closed, then this union is itself a CW complex, called a subcomplex. Thus the n-skeleton is the largest subcomplex of dimension n or less.
A CW complex is often constructed by defining its skeleta inductively. Begin by taking the 0-skeleton to be a discrete space
. Next, attach 1-cells to the 0-skeleton. Here, the 1-cells are attached to points of the 0-skeleton via some continuous map from unit 0-sphere, that is,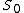 . Define the 1-skeleton to be the identification space obtained from the union of the 0-skeleton, 1-cells, and the identification of points of boundary of 1-cells by assigning an identification mapping from the boundary
. Define the 1-skeleton to be the identification space obtained from the union of the 0-skeleton, 1-cells, and the identification of points of boundary of 1-cells by assigning an identification mapping from the boundary
of the 1-cells into the 1-cells. In general, given the n-1-skeleton and a collection of (abstract) closed n-cells, as above, the n-cells are attached to the n-1-skeleton by some continuous mapping from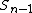 , and making an identification (equivalence relation) by specifying maps from the boundary of each n-cell into the n-1-skeleton. The n-skeleton is the identification space obtained from the union of the n-1-skeleton and the closed n-cells by identifying each point in the boundary of an n-cell with its image.
, and making an identification (equivalence relation) by specifying maps from the boundary of each n-cell into the n-1-skeleton. The n-skeleton is the identification space obtained from the union of the n-1-skeleton and the closed n-cells by identifying each point in the boundary of an n-cell with its image.
Up to isomorphism every n-dimensional complex can be obtained from its n-1 skeleton in this sense, and thus every finite-dimensional CW complex can be built up by the process above. This is true even for infinite-dimensional complexes, with the understanding that the result of the infinite process is the direct limit
of the skeleta: a set is closed in X if and only if it meets each skeleton in a closed set.
of CW-complexes is readily computable via cellular homology
. Moreover, in the category of CW-complexes and cellular maps, cellular homology
can be interpreted as a homology theory
. To compute an extraordinary (co)homology theory for a CW-complex, the Atiyah-Hirzebruch spectral sequence is the analogue of cellular homology
.
Some examples:
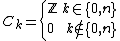
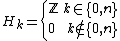 since all the differentials are zero.
since all the differentials are zero.
Alternatively, if we use the equatorial decomposition with two cells in every dimension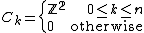 and the differentials are matrices of the form
and the differentials are matrices of the form 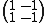 . This gives the same homology computation above, as the chain complex is exact at all terms
. This gives the same homology computation above, as the chain complex is exact at all terms
except and
and  .
.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a CW complex is a type of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
introduced by J. H. C. Whitehead
J. H. C. Whitehead
John Henry Constantine Whitehead FRS , known as Henry, was a British mathematician and was one of the founders of homotopy theory. He was born in Chennai , in India, and died in Princeton, New Jersey, in 1960....
to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
properties than simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
es, but still retains a combinatorial nature
that allows for computation.
Formulation
Roughly speaking, a CW-complex is made of basic building blocks called cells. The precise definition prescribes how the cells may be topologically glued together. The C stands for "closure-finite", and the W for "weak topology".An n-dimensional closed cell is a topological space that is homeomorphic to an n-dimensional closed ball. For example, a simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
is a closed cell, and more generally, a convex polytope
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
is a closed cell. An n-dimensional open cell is a topological space that is homeomorphic to the open ball. A 0-dimensional open (and closed) cell is a singleton space.
A CW complex is a Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
X together with a partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of X into open cells (of varying dimension) that satisfies two additional properties:
- For each n-dimensional open cell C in the set X, there exists a continuous map f from the n-dimensional closed ball to X such that
- the restriction of f from the interior of the n-dimensional ball is a homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
onto the cell C, and - the image of the boundaryBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the open ball, that is, under a homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
, the boundaryBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the open cell C, intersects only finitely many other cells.
- the restriction of f from the interior of the n-dimensional ball is a homeomorphism
- A subset of X is closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
if and only if it meets the closure of each cell in a closed set.
Inductive definition of CW-complexes
If the largest dimension of any of the cells is n, then the CW complex is said to have dimension n. If there is no bound to the cell dimensions then it is said to be infinite-dimensional. The n-skeletonN-skeleton
In mathematics, particularly in algebraic topology, the n-skeleton of a topological space X presented as a simplicial complex refers to the subspace Xn that is the union of the simplices of X of dimensions m ≤ n...
of a CW complex is the union of the cells whose dimension is at most n. If the union of a set of cells is closed, then this union is itself a CW complex, called a subcomplex. Thus the n-skeleton is the largest subcomplex of dimension n or less.
A CW complex is often constructed by defining its skeleta inductively. Begin by taking the 0-skeleton to be a discrete space
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
. Next, attach 1-cells to the 0-skeleton. Here, the 1-cells are attached to points of the 0-skeleton via some continuous map from unit 0-sphere, that is,
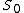 . Define the 1-skeleton to be the identification space obtained from the union of the 0-skeleton, 1-cells, and the identification of points of boundary of 1-cells by assigning an identification mapping from the boundary
. Define the 1-skeleton to be the identification space obtained from the union of the 0-skeleton, 1-cells, and the identification of points of boundary of 1-cells by assigning an identification mapping from the boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the 1-cells into the 1-cells. In general, given the n-1-skeleton and a collection of (abstract) closed n-cells, as above, the n-cells are attached to the n-1-skeleton by some continuous mapping from
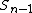 , and making an identification (equivalence relation) by specifying maps from the boundary of each n-cell into the n-1-skeleton. The n-skeleton is the identification space obtained from the union of the n-1-skeleton and the closed n-cells by identifying each point in the boundary of an n-cell with its image.
, and making an identification (equivalence relation) by specifying maps from the boundary of each n-cell into the n-1-skeleton. The n-skeleton is the identification space obtained from the union of the n-1-skeleton and the closed n-cells by identifying each point in the boundary of an n-cell with its image.Up to isomorphism every n-dimensional complex can be obtained from its n-1 skeleton in this sense, and thus every finite-dimensional CW complex can be built up by the process above. This is true even for infinite-dimensional complexes, with the understanding that the result of the infinite process is the direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of the skeleta: a set is closed in X if and only if it meets each skeleton in a closed set.
Examples
- The space
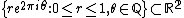 has the homotopy-type of a CW-complex (it is contractible) but it does not admit a CW-decomposition, since it is not locally contractible.
has the homotopy-type of a CW-complex (it is contractible) but it does not admit a CW-decomposition, since it is not locally contractible.
- The Hawaiian earringHawaiian earringIn mathematics, the Hawaiian earring H is the topological space defined by the union of circles in the Euclidean plane R2 with center and radius 1/n for n = 1, 2, 3, ......
is an example of a topological space that does not have the homotopy-type of a CW-complex.
- The standard CW-structure on the real numbers has 0-skeleton the integers
 and as 1-cells the intervals
and as 1-cells the intervals 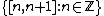 . Similarly, the standard CW-structure on
. Similarly, the standard CW-structure on  has cubical cells that are products of the 0 and 1-cells from
has cubical cells that are products of the 0 and 1-cells from  . This is the standard cubical lattice cell structure on
. This is the standard cubical lattice cell structure on  .
.
- A polyhedronPolyhedronIn elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
is naturally a CW-complex.
- A graphGraph (mathematics)In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
is a 1-dimensional CW-complex. Trivalent graphs can be considered as generic 1-dimensional CW-complexes. Specifically, if X is a 1-dimensional CW-complex, the attaching map for a 1-cell is a map from a two-point spaceDiscrete two-point spaceIn topology, a branch of mathematics, a discrete two-point space is the simplest example of a totally disconnected discrete space. The points can be denoted by the symbols 0 and 1....
to X, . This map can be perturbed to be disjoint from the 0-skeleton of X if and only if
. This map can be perturbed to be disjoint from the 0-skeleton of X if and only if 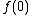 and
and  are not 0-valence vertices of X.
are not 0-valence vertices of X.
- The terminology for a generic 2-dimensional CW-complex is a shadow.
- The n-dimensional sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
admits a CW-structure with two cells, one 0-cell and one n-cell. Here the n-cell is attached by the constant mapping from to 0-cell. There is a popular alternative cell decomposition, since the equatorial inclusion
to 0-cell. There is a popular alternative cell decomposition, since the equatorial inclusion  has complement two balls: the upper and lower hemi-spheres. Inductively, this gives
has complement two balls: the upper and lower hemi-spheres. Inductively, this gives  a CW-decomposition with two cells in every dimension k such that
a CW-decomposition with two cells in every dimension k such that  .
.
- The n-dimensional real projective spaceProjective spaceIn mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
admits a CW-structure with one cell in each dimension.
- GrassmannianGrassmannianIn mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
manifolds admit a CW-structure called Schubert cells.
- ManifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, algebraic and projective varietiesAlgebraic varietyIn mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
have the homotopy-type of CW-complexes.
- The one-point compactificationAlexandroff extensionIn mathematical field of topology, the Alexandroff extension is a way to extend a noncompact topological space by adjoining a single point in such a way that the resulting space is compact. It is named for the Russian mathematician Pavel Alexandrov....
of a cusped hyperbolic manifoldHyperbolic manifoldIn mathematics, a hyperbolic n-manifold is a complete Riemannian n-manifold of constant sectional curvature -1.Every complete, connected, simply-connected manifold of constant negative curvature −1 is isometric to the real hyperbolic space Hn. As a result, the universal cover of any closed manifold...
has a canonical CW-decomposition with only one 0-cell (the compactification point) called the Epstein-Penner Decomposition. Such cell decompositions are frequently called ideal polyhedral decompositions and are used in popular computer software, SnapPeaSnapPeaSnapPea is free software designed to help mathematicians, in particular low-dimensional topologists, study hyperbolic 3-manifolds. The primary developer is Jeffrey Weeks, who created the first version as part of his doctoral thesis, supervised by William Thurston. The latest version is 3.0d3...
.
Homology and cohomology of CW-complexes
Singular homology and cohomologySingular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
of CW-complexes is readily computable via cellular homology
Cellular homology
In mathematics, cellular homology in algebraic topology is a homology theory for CW-complexes. It agrees with singular homology, and can provide an effective means of computing homology modules.- Definition :...
. Moreover, in the category of CW-complexes and cellular maps, cellular homology
Cellular homology
In mathematics, cellular homology in algebraic topology is a homology theory for CW-complexes. It agrees with singular homology, and can provide an effective means of computing homology modules.- Definition :...
can be interpreted as a homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
. To compute an extraordinary (co)homology theory for a CW-complex, the Atiyah-Hirzebruch spectral sequence is the analogue of cellular homology
Cellular homology
In mathematics, cellular homology in algebraic topology is a homology theory for CW-complexes. It agrees with singular homology, and can provide an effective means of computing homology modules.- Definition :...
.
Some examples:
- For the sphere
 , take the cell decomposition with two cells: a single 0-cell and a single n-cell. The cellular homology chain complex
, take the cell decomposition with two cells: a single 0-cell and a single n-cell. The cellular homology chain complex  and homology are given by:
and homology are given by:
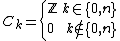
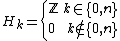 since all the differentials are zero.
since all the differentials are zero.Alternatively, if we use the equatorial decomposition with two cells in every dimension
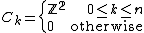 and the differentials are matrices of the form
and the differentials are matrices of the form 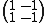 . This gives the same homology computation above, as the chain complex is exact at all terms
. This gives the same homology computation above, as the chain complex is exact at all termsexcept
 and
and  .
.- For
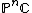 we get similarly
we get similarly
-

Both of the above examples are particularly simple because the homology is determined by the number of cells—i.e.: the cellular attaching maps have no role in these computations. This is a very special phenomenon and is not indicative of the general case.
Modification of CW-structures
There is a technique, developed by Whitehead, for replacing a CW-complex with a homotopy-equivalent CW-complex which has a simpler CW-decomposition.
Consider, for example, an arbitrary CW-complex. Its 1-skeleton can be fairly complicated, being an arbitrary graph. Now consider a maximal forest F in this graph. Since it is a collection of trees, and trees are contractible, consider the space where the equivalence relation is generated by
where the equivalence relation is generated by  if they are contained in a common tree in the maximal forest F. The quotient map
if they are contained in a common tree in the maximal forest F. The quotient map 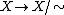 is a homotopy equivalence. Moreover,
is a homotopy equivalence. Moreover, 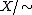 naturally inherits a CW-structure, with cells corresponding to the cells of
naturally inherits a CW-structure, with cells corresponding to the cells of  which are not contained in F. In particular, the 1-skeleton of
which are not contained in F. In particular, the 1-skeleton of  is a disjoint union of wedges of circles.
is a disjoint union of wedges of circles.
Another way of stating the above is that a connected CW-complex can be replaced by a homotopy-equivalent CW-complex whose 0-skeleton consists of a single point.
Consider climbing up the connectivity ladder—assume X is a simply-connected CW-complex whose 0-skeleton consists of a point. Can we, through suitable modifications, replace X by a homotopy-equivalent CW-complex where consists of a single point? The answer is yes. The first step is to observe that
consists of a single point? The answer is yes. The first step is to observe that  and the attaching maps to construct
and the attaching maps to construct  from
from  form a group presentationPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
form a group presentationPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
. The Tietze theoremTietze transformationsIn group theory, Tietze transformations are used to transform a given presentation of a group into another, often simpler presentation of the same group...
for group presentations states that there is a sequence of moves we can perform to reduce this group presentation to the trivial presentation of the trivial group. There are two Tietze moves:
- 1) Adding/removing a generator. Adding a generator, from the perspective of the CW-decomposition consists of adding a 1-cell and a 2-cell whose attaching map consists of the new 1-cell and the remainder of the attaching map is in
 . If we let
. If we let  be the corresponding CW-complex
be the corresponding CW-complex  then there is a homotopy-equivalence
then there is a homotopy-equivalence  given by sliding the new 2-cell into X.
given by sliding the new 2-cell into X.
- 2) Adding/removing a relation. The act of adding a relation is similar, only one is replacing X by
 where the new 3-cell has an attaching map that consists of the new 2-cell and remainder mapping into
where the new 3-cell has an attaching map that consists of the new 2-cell and remainder mapping into  . A similar slide gives a homotopy-equivalence
. A similar slide gives a homotopy-equivalence  .
.
If a CW-complex X is n-connected one can find a homotopy-equivalent CW-complex whose n-skeleton
whose n-skeleton  consists of a single point. The argument for
consists of a single point. The argument for 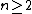 is similar to the
is similar to the  case, only one replaces Tietze moves for the fundamental group presentation by elementary matrix operations for the presentation matrices for
case, only one replaces Tietze moves for the fundamental group presentation by elementary matrix operations for the presentation matrices for 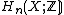 (using the presentation matrices coming from cellular homologyCellular homologyIn mathematics, cellular homology in algebraic topology is a homology theory for CW-complexes. It agrees with singular homology, and can provide an effective means of computing homology modules.- Definition :...
(using the presentation matrices coming from cellular homologyCellular homologyIn mathematics, cellular homology in algebraic topology is a homology theory for CW-complexes. It agrees with singular homology, and can provide an effective means of computing homology modules.- Definition :...
. i.e.: one can similarly realize elementary matrix operations by a sequence of addition/removal of cells or suitable homotopies of the attaching maps.
'The' homotopy category
The homotopy category of CW complexes is, in the opinion of some experts, the best if not the only candidate for the homotopy category (for technical reasons the version for pointed spacePointed spaceIn mathematics, a pointed space is a topological space X with a distinguished basepoint x0 in X. Maps of pointed spaces are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f = y0...
s is actually used). Auxiliary constructions that yield spaces that are not CW complexes must be used on occasion. One basic result is that the representable functorRepresentable functorIn mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
s on the homotopy category have a simple characterisation (the Brown representability theorem).
Properties
- CW-complexes are locally contractible.
- CW-complexes satisfy the Whitehead theoremWhitehead theoremIn homotopy theory , the Whitehead theorem states that if a continuous mapping f between topological spaces X and Y induces isomorphisms on all homotopy groups, then f is a homotopy equivalence provided X and Y are connected and have the homotopy-type of CW complexes. This result was proved by J....
-- ie: a map between CW-complexes is a homotopy-equivalence if and only if it induces an isomorphism on all homotopy groups.
- The product of two CW-complexes is a CW-complex. The weak topology on this product X×Y is the same as the more familiar product topologyProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
on most spaces of interest, but can be finerComparison of topologiesIn topology and related areas of mathematics comparison of topologies refers to the fact that two topological structures on a given set may stand in relation to each other. The set of all possible topologies on a given set forms a partially ordered set...
if X×Y has uncountably many cells and neither X nor Y is locally compactLocally compact spaceIn topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
.
- The function spaces Hom(X,Y) are not CW-complexes in general but are homotopy equivalent to CW-complexes by a theorem of John MilnorJohn MilnorJohn Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
(1959). Actual function spaces occur in the somewhat larger category of compactly generated Hausdorff spaces.
- A covering space of a CW complex is also a CW complex.
- CW-complexes are paracompact
See also
- The notion of CW-complex has an adaptation to smooth manifoldsDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
called a handle decomposition which is closely related to surgery theorySurgery theoryIn mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
.
General references
- J. H. C. Whitehead, Combinatorial homotopy. I., Bull. Amer. Math. Soc. 55 (1949), 213–245
- J. H. C. Whitehead, Combinatorial homotopy. II., Bull. Amer. Math. Soc. 55 (1949), 453–496
- Hatcher, AllenAllen HatcherAllen Edward Hatcher is an American topologist and also a noted author. His book Algebraic Topology, which is the first in a series, is considered by many to be one of the best introductions to the subject....
, Algebraic topology, Cambridge University Press (2002). ISBN 0-521-79540-0. This textbook defines CW complexes in the first chapter and uses them throughout; includes an appendix on the topology of CW complexes. A free electronic version is available on the author's homepage. - A. T. Lundell and S. Weingram, The topology of CW complexes, Van Nostrand University Series in Higher Mathematics (1970), ISBN 0-442-04910-2
- 1) Adding/removing a generator. Adding a generator, from the perspective of the CW-decomposition consists of adding a 1-cell and a 2-cell whose attaching map consists of the new 1-cell and the remainder of the attaching map is in

