Gauss–Bonnet theorem
Encyclopedia
The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surface
s which connects their geometry (in the sense of curvature
) to their topology (in the sense of the Euler characteristic
). It is named after Carl Friedrich Gauss
who was aware of a version of the theorem but never published it, and Pierre Ossian Bonnet
who published a special case in 1848.
is a compact
two-dimensional Riemannian manifold
with boundary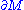
. Let 
be the Gaussian curvature
of
, and let 
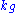be the geodesic curvature
of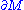
. Then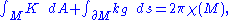
where dA is the element of area
of the surface, and ds is the line element along the boundary of M. Here,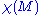
is the Euler characteristic
of
.
If the boundary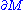
is piecewise smooth, then we interpret the integral 
as the sum of the corresponding integrals along the smooth portions of the boundary, plus the sum of the angle
s by which the smooth portions turn at the corners of the boundary.
can be omitted. It states that the total Gaussian curvature of such a closed surface is equal to 2π times the Euler characteristic of the surface. Note that for orientable compact surfaces without boundary, the Euler characteristic equals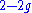
, where 
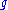is the genus
of the surface: Any orientable compact surface without boundary is topologically equivalent to a sphere with some handles attached, and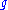
counts the
number of handles.
If one bends and deforms the surface
, its Euler characteristic, being a topological invariant, will not change, while the curvatures at some points will. The theorem states, somewhat surprisingly, that the
total integral of all curvatures will remain the same, no matter how the deforming is done. So for instance if you have a sphere with a "dent", then its total curvature is 4π (the Euler characteristic of a sphere being 2), no matter how big or deep the dent.
Compactness of the surface is of crucial importance. Consider for instance the open unit disc, a non-compact Riemann surface without boundary, with curvature 0 and with Euler characteristic 1: the Gauss–Bonnet formula does not work. It holds true however for the compact closed unit disc, which also has Euler characteristic 1, because of the added boundary integral with value 2π.
As an application, a torus
has Euler characteristic 0, so its total curvature must also be zero. If the torus carries the ordinary Riemannian metric from its embedding in R3, then the inside has negative Gaussian curvature, the outside has positive Gaussian curvature, and the total curvature is indeed 0. It is also possible to construct a torus by identifying opposite sides of a square, in which case the Riemannian metric on the torus is flat and has constant curvature 0, again resulting in total curvature 0. It is not possible to specify a Riemannian metric on the torus with everywhere positive or everywhere negative Gaussian curvature.
The theorem also has interesting consequences for triangles. Suppose M is some 2-dimensional Riemannian manifold (not necessarily compact), and we specify a "triangle" on M formed by three geodesic
s. Then we can apply Gauss–Bonnet to the surface T formed by the inside of that triangle and the piecewise boundary given by the triangle itself. The geodesic curvature of geodesics being zero, and the Euler characteristic of T being 1, the theorem then states that the sum of the turning angles of the geodesic triangle is equal to 2π minus the total curvature within the triangle. Since the turning angle at a corner is equal to π minus the interior angle, we can rephrase this as follows:
In the case of the plane (where the Gaussian curvature is 0 and geodesics are straight lines), we recover the familiar formula for the sum of angles in an ordinary triangle. On the standard sphere, where the curvature is everywhere 1, we see that the angle sum of geodesic triangles is always bigger than π.
and hyperbolic trigonometry
, the area of a triangle is proportional to the amount by which its interior angles fail to add up to 180°, or equivalently by the (inverse) amount by which its exterior angles fail to add up to 360°.
The area of a spherical triangle is proportional to its excess, by Girard's theorem – the amount by which its interior angles add up to more than 180°, which is equal to the amount by which its exterior angles add up to less than 360°.
The area of a hyperbolic triangle
, conversely is proportional to its defect, as established by Johann Heinrich Lambert
.
is the polyhedral analog:
it states that the sum of the defect at all the vertices of a polyhedron which is homeomorphic to the sphere is 4π. More generally, if the polyhedron has Euler characteristic
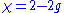(where g is the genus, meaning "number of holes"), then the sum of the defect is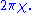 
This is the special case of Gauss–Bonnet, where the curvature is concentrated at discrete points (the vertices).
Thinking of curvature as a measure
, rather than as a function, Descartes' theorem is Gauss–Bonnet where the curvature is a discrete measure
, and Gauss–Bonnet for measures generalizes both Gauss–Bonnet for smooth manifolds and Descartes' theorem.
be a finite 2-dimensional pseudo-manifold. Let 
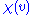denote the number of triangles containing the vertex 
. Then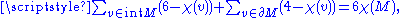
where the first sum ranges over the vertices in the interior of
, the second sum is over the boundary vertices, and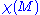 
is the Euler characteristic of 
.
More specifically, if
is a closed digital 2-dimensional manifold
,
The genus
where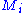
indicates the set of surface-points each of which has 
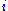adjacent points on the surface. See digital topology
, Weil
, and Chern
; see generalized Gauss–Bonnet theorem and Chern–Weil homomorphism. The Riemann–Roch theorem
can also be seen as a generalization of Gauss–Bonnet.
An extremely far-reaching generalization of all the above-mentioned theorems is the Atiyah–Singer index theorem
.
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s which connects their geometry (in the sense of curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
) to their topology (in the sense of the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
). It is named after Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
who was aware of a version of the theorem but never published it, and Pierre Ossian Bonnet
Pierre Ossian Bonnet
Pierre Ossian Bonnet was a French mathematician. He made some important contributions to the differential geometry of surfaces, including the Gauss-Bonnet theorem.-Early years:...
who published a special case in 1848.
Statement of the theorem
Suppose is a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
two-dimensional Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
with boundary
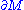. Let be the Gaussian curvatureGaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
of
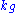, and let be the geodesic curvatureGeodesic curvature
In Riemannian geometry, the geodesic curvature k_g of a curve lying on a submanifold of the ambient space measures how far the curve is from being a geodesic...
of
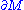. Then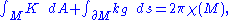where dA is the element of area
Volume element
In mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates...
of the surface, and ds is the line element along the boundary of M. Here,
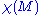is the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of
.If the boundary
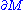is piecewise smooth, then we interpret the integral as the sum of the corresponding integrals along the smooth portions of the boundary, plus the sum of the angleAngle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s by which the smooth portions turn at the corners of the boundary.
Interpretation and significance
The theorem applies in particular to compact surfaces without boundary, in which case the integralcan be omitted. It states that the total Gaussian curvature of such a closed surface is equal to 2π times the Euler characteristic of the surface. Note that for orientable compact surfaces without boundary, the Euler characteristic equals
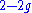, where 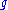is the genusGenus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
of the surface: Any orientable compact surface without boundary is topologically equivalent to a sphere with some handles attached, and
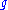counts thenumber of handles.
If one bends and deforms the surface
, its Euler characteristic, being a topological invariant, will not change, while the curvatures at some points will. The theorem states, somewhat surprisingly, that thetotal integral of all curvatures will remain the same, no matter how the deforming is done. So for instance if you have a sphere with a "dent", then its total curvature is 4π (the Euler characteristic of a sphere being 2), no matter how big or deep the dent.
Compactness of the surface is of crucial importance. Consider for instance the open unit disc, a non-compact Riemann surface without boundary, with curvature 0 and with Euler characteristic 1: the Gauss–Bonnet formula does not work. It holds true however for the compact closed unit disc, which also has Euler characteristic 1, because of the added boundary integral with value 2π.
As an application, a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
has Euler characteristic 0, so its total curvature must also be zero. If the torus carries the ordinary Riemannian metric from its embedding in R3, then the inside has negative Gaussian curvature, the outside has positive Gaussian curvature, and the total curvature is indeed 0. It is also possible to construct a torus by identifying opposite sides of a square, in which case the Riemannian metric on the torus is flat and has constant curvature 0, again resulting in total curvature 0. It is not possible to specify a Riemannian metric on the torus with everywhere positive or everywhere negative Gaussian curvature.
The theorem also has interesting consequences for triangles. Suppose M is some 2-dimensional Riemannian manifold (not necessarily compact), and we specify a "triangle" on M formed by three geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s. Then we can apply Gauss–Bonnet to the surface T formed by the inside of that triangle and the piecewise boundary given by the triangle itself. The geodesic curvature of geodesics being zero, and the Euler characteristic of T being 1, the theorem then states that the sum of the turning angles of the geodesic triangle is equal to 2π minus the total curvature within the triangle. Since the turning angle at a corner is equal to π minus the interior angle, we can rephrase this as follows:
- The sum of interior angles of a geodesic triangle is equal to π plus the total curvature enclosed by the triangle.
In the case of the plane (where the Gaussian curvature is 0 and geodesics are straight lines), we recover the familiar formula for the sum of angles in an ordinary triangle. On the standard sphere, where the curvature is everywhere 1, we see that the angle sum of geodesic triangles is always bigger than π.
Special cases
A number of earlier results in spherical geometry and hyperbolic geometry over the preceding centuries were subsumed as special cases of Gauss–Bonnet.Triangles
In spherical trigonometrySpherical trigonometry
Spherical trigonometry is a branch of spherical geometry which deals with polygons on the sphere and the relationships between the sides and the angles...
and hyperbolic trigonometry
Hyperbolic trigonometry
In mathematics, hyperbolic trigonometry can mean:*The use of the hyperbolic functions*The use of gyrotrigonometry in hyperbolic geometry...
, the area of a triangle is proportional to the amount by which its interior angles fail to add up to 180°, or equivalently by the (inverse) amount by which its exterior angles fail to add up to 360°.
The area of a spherical triangle is proportional to its excess, by Girard's theorem – the amount by which its interior angles add up to more than 180°, which is equal to the amount by which its exterior angles add up to less than 360°.
The area of a hyperbolic triangle
Hyperbolic triangle
In mathematics, the term hyperbolic triangle has more than one meaning.-Hyperbolic geometry:In hyperbolic geometry, a hyperbolic triangle is a figure in the hyperbolic plane, analogous to a triangle in Euclidean geometry, consisting of three sides and three angles...
, conversely is proportional to its defect, as established by Johann Heinrich Lambert
Johann Heinrich Lambert
Johann Heinrich Lambert was a Swiss mathematician, physicist, philosopher and astronomer.Asteroid 187 Lamberta was named in his honour.-Biography:...
.
Polyhedra
Descartes' theorem on total angular defect of a polyhedronPolyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
is the polyhedral analog:
it states that the sum of the defect at all the vertices of a polyhedron which is homeomorphic to the sphere is 4π. More generally, if the polyhedron has Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
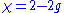(where g is the genus, meaning "number of holes"), then the sum of the defect is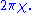 This is the special case of Gauss–Bonnet, where the curvature is concentrated at discrete points (the vertices).
Thinking of curvature as a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, rather than as a function, Descartes' theorem is Gauss–Bonnet where the curvature is a discrete measure
Discrete measure
In mathematics, more precisely in measure theory, a measure on the real line is called a discrete measure if its support is at most a countable set. Note that the support need not be a discrete set...
, and Gauss–Bonnet for measures generalizes both Gauss–Bonnet for smooth manifolds and Descartes' theorem.
Combinatorial analog
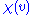There are several combinatorial analogs of the Gauss–Bonnet theorem. We state the following one. Let be a finite 2-dimensional pseudo-manifold. Let denote the number of triangles containing the vertex . Then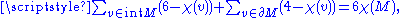where the first sum ranges over the vertices in the interior of
, the second sum is over the boundary vertices, and 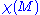is the Euler characteristic of .More specifically, if
is a closed digital 2-dimensional manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
,
The genus
where
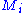indicates the set of surface-points each of which has 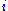adjacent points on the surface. See digital topologyDigital topology
Digital topology deals with properties and features of two-dimensional or three-dimensional digital imagesthat correspond to topological properties or topological features of objects....
Generalizations
Generalizations of the Gauss–Bonnet theorem to n-dimensional Riemannian manifolds were found in the 1940s, by AllendoerferCarl B. Allendoerfer
Carl Barnett Allendoerfer was a prominent American mathematician in the mid-twentieth century, known for his work in topology and mathematics education.-Background:...
, Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
, and Chern
Shiing-Shen Chern
Shiing-Shen Chern was a Chinese American mathematician, one of the leaders in differential geometry of the twentieth century.-Early years in China:...
; see generalized Gauss–Bonnet theorem and Chern–Weil homomorphism. The Riemann–Roch theorem
Riemann–Roch theorem
The Riemann–Roch theorem is an important tool in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeroes and allowed poles...
can also be seen as a generalization of Gauss–Bonnet.
An extremely far-reaching generalization of all the above-mentioned theorems is the Atiyah–Singer index theorem
Atiyah–Singer index theorem
In differential geometry, the Atiyah–Singer index theorem, proved by , states that for an elliptic differential operator on a compact manifold, the analytical index is equal to the topological index...
.
External links
- Gauss–Bonnet Theorem at Wolfram Mathworld