General linear group
Encyclopedia
In mathematics
, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication
. This forms a group
, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible. The group is so named because the columns of an invertible matrix are linearly independent, hence the vectors/points they define are in general linear position, and matrices in the general linear group take points in general linear position to points in general linear position.
To be more precise, it is necessary to specify what kind of objects may appear in the entries of the matrix. For example, the general linear group over R (the set of real numbers) is the group of n×n invertible matrices of real numbers, and is denoted by GLn(R) or GL(n, R).
More generally, the general linear group of degree n over any field
F (such as the complex number
s), or a ring
R (such as the ring of integer
s), is the set of n×n invertible matrices with entries from F (or R), again with matrix multiplication as the group operation. Typical notation is GLn(F) or GL(n, F), or simply GL(n) if the field is understood.
More generally still, the general linear group of a vector space GL(V) is the abstract automorphism group, not necessarily written as matrices.
The special linear group, written SL(n, F) or SLn(F), is the subgroup
of GL(n, F) consisting of matrices with a determinant
of 1.
The group GL(n, F) and its subgroups are often called linear groups or matrix groups (the abstract group GL(V) is a linear group but not a matrix group). These groups are important in the theory of group representation
s, and also arise in the study of spatial symmetries
and symmetries of vector space
s in general, as well as the study of polynomials. The modular group
may be realised as a quotient of the special linear group SL(2, Z).
If n ≥ 2, then the group GL(n, F) is not abelian
.
over the field F, the general linear group of V, written GL(V) or Aut(V), is the group of all automorphism
s of V, i.e. the set of all bijective linear transformation
s V → V, together with functional composition as group operation. If V has finite dimension n, then GL(V) and GL(n, F) are isomorphic
. The isomorphism is not canonical
; it depends on a choice of basis
in V. Given a basis (e1, ..., en) of V and an automorphism T in GL(V), we have
for some constants ajk in F; the matrix corresponding to T is then just the matrix with entries given by the ajk.
In a similar way, for a commutative ring R the group GL(n, R) may be interpreted as the group of automorphisms of a free
R-module M of rank n. One can also define GL(M) for any R-module, but in general this is not isomorphic to GL(n, R) (for any n).
is nonzero. Therefore an alternative definition of GL(n, F) is as the group of matrices with nonzero determinant.
Over a commutative ring
R, one must be slightly more careful: a matrix over R is invertible if and only if its determinant is a unit
in R, that is, if its determinant is invertible in R. Therefore GL(n, R) may be defined as the group of matrices whose determinants are units.
Over a non-commutative ring R, determinants are not at all well behaved. In this case, GL(n, R) may be defined as the unit group of the matrix ring
M(n, R).
s is a real Lie group
of dimension n2. To see this, note that the set of all n×n real matrices, Mn(R), forms a real vector space of dimension n2. The subset GL(n,R) consists of those matrices whose determinant
is non-zero. The determinant is a polynomial
map, and hence GL(n,R) is an open affine subvariety
of Mn(R) (a non-empty open subset of Mn(R) in the Zariski topology
), and therefore
a smooth manifold of the same dimension.
The Lie algebra
of GL(n,R), denoted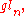 consists of all n×n real matrices with the commutator
consists of all n×n real matrices with the commutator
serving as the Lie bracket.
As a manifold, GL(n,R) is not connected
but rather has two connected components
: the matrices with positive determinant and the ones with negative determinant. The identity component
, denoted by GL+(n, R), consists of the real n×n matrices with positive determinant. This is also a Lie group of dimension n2; it has the same Lie algebra as GL(n,R).
The group GL(n,R) is also noncompact
. "The" maximal compact subgroup
of GL(n, R) is the orthogonal group
O(n), while "the" maximal compact subgroup of GL+(n, R) is the special orthogonal group SO(n). As for SO(n), the group GL+(n, R) is not simply connected (except when n=1), but rather has a fundamental group
isomorphic to Z for n=2 or Z2 for n>2.
s is a complex Lie group
of complex dimension n2. As a real Lie group it has dimension 2n2. The set of all real matrices forms a real Lie subgroup. These correspond to the inclusions
which have real dimensions n2, 2n2, and 4n2 = (2n)2. Complex n-dimensional matrices can be characterized as real 2n-dimensional matrices that preserve a linear complex structure
– concretely, that commute with a matrix J such that J2 =−I, where J corresponds to multiplying by the imaginary unit i.
The Lie algebra
corresponding to GL(n,C) consists of all n×n complex matrices with the commutator
serving as the Lie bracket.
Unlike the real case, GL(n,C) is connected
. This follows, in part, since the multiplicative group of complex numbers C* is connected. The group manifold GL(n,C) is not compact; rather its maximal compact subgroup
is the unitary group
U(n). As for U(n), the group manifold GL(n,C) is not simply connected but has a fundamental group
isomorphic to Z.
with q elements, then we sometimes write GL(n, q) instead of GL(n, F). When p is prime, GL(n, p) is the outer automorphism group
of the group Zpn, and also the automorphism
group, because Zpn is Abelian, so the inner automorphism group is trivial.
The order of GL(n, q) is:(qn − q)(qn − q2) … (qn − qn−1)
This can be shown by counting the possible columns of the matrix: the first column can be anything but the zero vector; the second column can be anything but the multiples of the first column; and in general, the kth column can be any vector not in the linear span
of the first k − 1 columns. In q-analog
notation, this is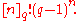
For example, GL(3, 2) has order (8 − 1)(8 − 2)(8 − 4) = 168. It is the automorphism group of the Fano plane
and of the group Z23, and is also known as PSL(2,7)
.
More generally, one can count points of Grassmannian
over F: in other words the number of subspaces of a given dimension k. This requires only finding the order of the stabilizer subgroup of one such subspace and dividing into the formula just given, by the orbit-stabilizer theorem.
These formulas are connected to the Schubert decomposition of the Grassmannian, and are q-analogs
of the Betti number
s of complex Grassmannians. This was one of the clues leading to the Weil conjectures
.
Note that in the limit as the order of GL(n, q) goes to
the order of GL(n, q) goes to  which is the order of the symmetric group – in the philosophy of the field with one element
which is the order of the symmetric group – in the philosophy of the field with one element
, one thus interprets the symmetric group
as the general linear group over the field with one element: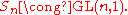
in 1832, in his last letter (to Chevalier) and second (of three) attached manuscripts, which he used in the context of studying the Galois group
of the general equation of order pν.
1. They are special in that they lie on a subvariety
– they satisfy a polynomial equation (as the determinant is a polynomial in the entries). Matrices of this type form a group as the determinant of the product of two matrices is the product of the determinants of each matrix. SL(n, F) is a normal subgroup
of GL(n, F).
If we write F× for the multiplicative group
of F (excluding 0), then the determinant is a group homomorphism
The kernel
of the map is just the special linear group. By the first isomorphism theorem we see that GL(n,F)/SL(n,F) is isomorphic to F×. In fact, GL(n, F) can be written as a semidirect product
of SL(n, F) by F×:
When F is R or C, SL(n) is a Lie subgroup
of GL(n) of dimension n2 − 1. The Lie algebra
of SL(n) consists of all n×n matrices over F with vanishing trace. The Lie bracket is given by the commutator
.
The special linear group SL(n, R) can be characterized as the group of volume
and orientation
preserving linear transformations of Rn.
The group SL(n, C) is simply connected while SL(n, R) is not. SL(n, R) has the same fundamental group as GL+(n, R), that is, Z for n=2 and Z2 for n>2.
forms a subgroup of GL(n, F) isomorphic to (F×)n. In fields like R and C, these correspond to rescaling the space; the so called dilations and contractions.
A scalar matrix is a diagonal matrix which is a constant times the identity matrix
. The set of all nonzero scalar matrices forms a subgroup of GL(n, F) isomorphic to F× . This group is the center of GL(n, F). In particular, it is a normal, abelian subgroup.
The center of SL(n, F) is simply the set of all scalar matrices with unit determinant, and is isomorphic to the group of nth roots of unity in the field F.
These groups provide important examples of Lie groups.
PGL(n, F) and the projective special linear group PSL(n,F) are the quotients
of GL(n,F) and SL(n,F) by their centers (which consist of the multiples of the identity matrix therein); they are the induced action
on the associated projective space
.
Aff(n,F) is an extension
of GL(n,F) by the group of translations in Fn. It can be written as a semidirect product
:
where GL(n, F) acts on Fn in the natural manner. The affine group can be viewed as the group of all affine transformation
s of the affine space
underlying the vector space Fn.
One has analogous constructions for other subgroups of the general linear group: for instance, the special affine group
is the subgroup defined by the semidirect product, SL(n, F) ⋉ Fn, and the Poincaré group
is the affine group associated to the Lorentz group
, O(1,3,F) ⋉ Fn.
s, and contains GL. A semilinear transformation is a transformation which is linear "up to a twist", meaning "up to a field automorphism under scalar multiplication". It can be written as a semidirect product:
where Gal(F) is the Galois group
of F (over its prime field), which acts on GL(n, F) by the Galois action on the entries.
The main interest of ΓL(n, F) is that the associated projective semilinear group PΓL(n, F) (which contains PGL(n, F)) is the collineation group of projective space
, for n > 2, and thus semilinear maps are of interest in projective geometry
.
general linear group is the direct limit
of the inclusions as the upper left block matrix
as the upper left block matrix
. It is denoted by either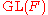 or
or  , and can also be interpreted as invertible infinite matrices which differ from the identity matrix in only finitely many places.
, and can also be interpreted as invertible infinite matrices which differ from the identity matrix in only finitely many places.
It is used in algebraic K-theory
to define K1, and over the reals has a well-understood topology, thanks to Bott periodicity.
It should not be confused with the space of (bounded) invertible operators on a Hilbert space
, which is a larger group, and topologically much simpler, namely contractible – see Kuiper's theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. This forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible. The group is so named because the columns of an invertible matrix are linearly independent, hence the vectors/points they define are in general linear position, and matrices in the general linear group take points in general linear position to points in general linear position.
To be more precise, it is necessary to specify what kind of objects may appear in the entries of the matrix. For example, the general linear group over R (the set of real numbers) is the group of n×n invertible matrices of real numbers, and is denoted by GLn(R) or GL(n, R).
More generally, the general linear group of degree n over any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F (such as the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s), or a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R (such as the ring of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s), is the set of n×n invertible matrices with entries from F (or R), again with matrix multiplication as the group operation. Typical notation is GLn(F) or GL(n, F), or simply GL(n) if the field is understood.
More generally still, the general linear group of a vector space GL(V) is the abstract automorphism group, not necessarily written as matrices.
The special linear group, written SL(n, F) or SLn(F), is the subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of GL(n, F) consisting of matrices with a determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of 1.
The group GL(n, F) and its subgroups are often called linear groups or matrix groups (the abstract group GL(V) is a linear group but not a matrix group). These groups are important in the theory of group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s, and also arise in the study of spatial symmetries
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
and symmetries of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s in general, as well as the study of polynomials. The modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
may be realised as a quotient of the special linear group SL(2, Z).
If n ≥ 2, then the group GL(n, F) is not abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
.
General linear group of a vector space
If V is a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the field F, the general linear group of V, written GL(V) or Aut(V), is the group of all automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s of V, i.e. the set of all bijective linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s V → V, together with functional composition as group operation. If V has finite dimension n, then GL(V) and GL(n, F) are isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
. The isomorphism is not canonical
Canonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
; it depends on a choice of basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
in V. Given a basis (e1, ..., en) of V and an automorphism T in GL(V), we have
for some constants ajk in F; the matrix corresponding to T is then just the matrix with entries given by the ajk.
In a similar way, for a commutative ring R the group GL(n, R) may be interpreted as the group of automorphisms of a free
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
R-module M of rank n. One can also define GL(M) for any R-module, but in general this is not isomorphic to GL(n, R) (for any n).
In terms of determinants
Over a field F, a matrix is invertible if and only if its determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is nonzero. Therefore an alternative definition of GL(n, F) is as the group of matrices with nonzero determinant.
Over a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R, one must be slightly more careful: a matrix over R is invertible if and only if its determinant is a unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
in R, that is, if its determinant is invertible in R. Therefore GL(n, R) may be defined as the group of matrices whose determinants are units.
Over a non-commutative ring R, determinants are not at all well behaved. In this case, GL(n, R) may be defined as the unit group of the matrix ring
Matrix ring
In abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
M(n, R).
Real case
The general linear group GL(n,R) over the field of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is a real Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of dimension n2. To see this, note that the set of all n×n real matrices, Mn(R), forms a real vector space of dimension n2. The subset GL(n,R) consists of those matrices whose determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is non-zero. The determinant is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
map, and hence GL(n,R) is an open affine subvariety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
of Mn(R) (a non-empty open subset of Mn(R) in the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
), and therefore
a smooth manifold of the same dimension.
The Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of GL(n,R), denoted
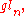 consists of all n×n real matrices with the commutator
consists of all n×n real matrices with the commutatorCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
serving as the Lie bracket.
As a manifold, GL(n,R) is not connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
but rather has two connected components
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
: the matrices with positive determinant and the ones with negative determinant. The identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
, denoted by GL+(n, R), consists of the real n×n matrices with positive determinant. This is also a Lie group of dimension n2; it has the same Lie algebra as GL(n,R).
The group GL(n,R) is also noncompact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. "The" maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
of GL(n, R) is the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(n), while "the" maximal compact subgroup of GL+(n, R) is the special orthogonal group SO(n). As for SO(n), the group GL+(n, R) is not simply connected (except when n=1), but rather has a fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
isomorphic to Z for n=2 or Z2 for n>2.
Complex case
The general linear GL(n,C) over the field of complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s is a complex Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of complex dimension n2. As a real Lie group it has dimension 2n2. The set of all real matrices forms a real Lie subgroup. These correspond to the inclusions
- GL(n,R) < GL(n,C) < GL(2n,R),
which have real dimensions n2, 2n2, and 4n2 = (2n)2. Complex n-dimensional matrices can be characterized as real 2n-dimensional matrices that preserve a linear complex structure
Linear complex structure
In mathematics, a complex structure on a real vector space V is an automorphism of V that squares to the minus identity, −I. Such a structure on V allows one to define multiplication by complex scalars in a canonical fashion so as to regard V as a complex vector space.Complex structures have...
– concretely, that commute with a matrix J such that J2 =−I, where J corresponds to multiplying by the imaginary unit i.
The Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
corresponding to GL(n,C) consists of all n×n complex matrices with the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
serving as the Lie bracket.
Unlike the real case, GL(n,C) is connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
. This follows, in part, since the multiplicative group of complex numbers C* is connected. The group manifold GL(n,C) is not compact; rather its maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
is the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
U(n). As for U(n), the group manifold GL(n,C) is not simply connected but has a fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
isomorphic to Z.
Over finite fields
If F is a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with q elements, then we sometimes write GL(n, q) instead of GL(n, F). When p is prime, GL(n, p) is the outer automorphism group
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
of the group Zpn, and also the automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
group, because Zpn is Abelian, so the inner automorphism group is trivial.
The order of GL(n, q) is:(qn − q)(qn − q2) … (qn − qn−1)
This can be shown by counting the possible columns of the matrix: the first column can be anything but the zero vector; the second column can be anything but the multiples of the first column; and in general, the kth column can be any vector not in the linear span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
of the first k − 1 columns. In q-analog
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
notation, this is
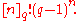
For example, GL(3, 2) has order (8 − 1)(8 − 2)(8 − 4) = 168. It is the automorphism group of the Fano plane
Fano plane
In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
and of the group Z23, and is also known as PSL(2,7)
PSL(2,7)
In mathematics, the projective special linear group PSL is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane...
.
More generally, one can count points of Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
over F: in other words the number of subspaces of a given dimension k. This requires only finding the order of the stabilizer subgroup of one such subspace and dividing into the formula just given, by the orbit-stabilizer theorem.
These formulas are connected to the Schubert decomposition of the Grassmannian, and are q-analogs
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
of the Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s of complex Grassmannians. This was one of the clues leading to the Weil conjectures
Weil conjectures
In mathematics, the Weil conjectures were some highly-influential proposals by on the generating functions derived from counting the number of points on algebraic varieties over finite fields....
.
Note that in the limit as
 the order of GL(n, q) goes to
the order of GL(n, q) goes to  which is the order of the symmetric group – in the philosophy of the field with one element
which is the order of the symmetric group – in the philosophy of the field with one elementField with one element
In mathematics, the field with one element is a suggestive name for an object that should behave similarly to a finite field with a single element, if such a field could exist. This object is denoted F1, or, in a French-English pun, Fun...
, one thus interprets the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
as the general linear group over the field with one element:
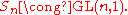
History
The general linear group over a prime field, GL(ν,p), was constructed and its order computed by Évariste GaloisÉvariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
in 1832, in his last letter (to Chevalier) and second (of three) attached manuscripts, which he used in the context of studying the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of the general equation of order pν.
Special linear group
The special linear group, SL(n, F), is the group of all matrices with determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1. They are special in that they lie on a subvariety
Subvariety
In botanical nomenclature, a subvariety is a taxonomic rank below that of variety but above that of form : it is an infraspecific taxon. Its name consists of three parts: a genus name, a specific epithet and an infraspecific epithet. To indicate the rank, the abbreviation "subvar." should be put...
– they satisfy a polynomial equation (as the determinant is a polynomial in the entries). Matrices of this type form a group as the determinant of the product of two matrices is the product of the determinants of each matrix. SL(n, F) is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of GL(n, F).
If we write F× for the multiplicative group
Multiplicative group
In mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
of F (excluding 0), then the determinant is a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
- det: GL(n, F) → F×.
The kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of the map is just the special linear group. By the first isomorphism theorem we see that GL(n,F)/SL(n,F) is isomorphic to F×. In fact, GL(n, F) can be written as a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of SL(n, F) by F×:
- GL(n, F) = SL(n, F) ⋊ F×
When F is R or C, SL(n) is a Lie subgroup
Lie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...
of GL(n) of dimension n2 − 1. The Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of SL(n) consists of all n×n matrices over F with vanishing trace. The Lie bracket is given by the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
.
The special linear group SL(n, R) can be characterized as the group of volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
and orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
preserving linear transformations of Rn.
The group SL(n, C) is simply connected while SL(n, R) is not. SL(n, R) has the same fundamental group as GL+(n, R), that is, Z for n=2 and Z2 for n>2.
Diagonal subgroups
The set of all invertible diagonal matricesDiagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
forms a subgroup of GL(n, F) isomorphic to (F×)n. In fields like R and C, these correspond to rescaling the space; the so called dilations and contractions.
A scalar matrix is a diagonal matrix which is a constant times the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. The set of all nonzero scalar matrices forms a subgroup of GL(n, F) isomorphic to F× . This group is the center of GL(n, F). In particular, it is a normal, abelian subgroup.
The center of SL(n, F) is simply the set of all scalar matrices with unit determinant, and is isomorphic to the group of nth roots of unity in the field F.
Classical groups
The so-called classical groups are subgroups of GL(V) which preserve some sort of bilinear form on a vector space V. These include the- orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
, O(V), which preserves a non-degenerate quadratic formQuadratic formIn mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
on V, - symplectic groupSymplectic groupIn mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
, Sp(V), which preserves a symplectic formSymplectic vector spaceIn mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
on V (a non-degenerate alternating form), - unitary groupUnitary groupIn mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
, U(V), which, when F = C, preserves a non-degenerate hermitian form on V.
These groups provide important examples of Lie groups.
Projective linear group
The projective linear groupProjective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
PGL(n, F) and the projective special linear group PSL(n,F) are the quotients
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of GL(n,F) and SL(n,F) by their centers (which consist of the multiples of the identity matrix therein); they are the induced action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on the associated projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
.
Affine group
The affine groupAffine group
In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
Aff(n,F) is an extension
Group extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
of GL(n,F) by the group of translations in Fn. It can be written as a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
:
- Aff(n, F) = GL(n, F) ⋉ Fn
where GL(n, F) acts on Fn in the natural manner. The affine group can be viewed as the group of all affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s of the affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
underlying the vector space Fn.
One has analogous constructions for other subgroups of the general linear group: for instance, the special affine group
Special affine group
In the mathematical study of transformation groups, the special affine group is the group of affine transformations of a fixed affine space which preserve volume...
is the subgroup defined by the semidirect product, SL(n, F) ⋉ Fn, and the Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
is the affine group associated to the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
, O(1,3,F) ⋉ Fn.
General semilinear group
The general semilinear group ΓL(n,F) is the group of all invertible semilinear transformationSemilinear transformation
In linear algebra, particularly projective geometry, a semilinear transformation between vector spaces V and W over a field K is a function that is a linear transformation "up to a twist", hence semi-linear, where "twist" means "field automorphism of K"...
s, and contains GL. A semilinear transformation is a transformation which is linear "up to a twist", meaning "up to a field automorphism under scalar multiplication". It can be written as a semidirect product:
- ΓL(n, F) = Gal(F) ⋉ GL(n, F)
where Gal(F) is the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of F (over its prime field), which acts on GL(n, F) by the Galois action on the entries.
The main interest of ΓL(n, F) is that the associated projective semilinear group PΓL(n, F) (which contains PGL(n, F)) is the collineation group of projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, for n > 2, and thus semilinear maps are of interest in projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
.
Infinite general linear group
The infinite general linear group or stableDirect limit of groups
In mathematics, a direct limit of groups is the direct limit of a direct system of groups. These are central objects of study in algebraic topology, especially stable homotopy theory and homological algebra...
general linear group is the direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of the inclusions
 as the upper left block matrix
as the upper left block matrixBlock matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
. It is denoted by either
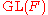 or
or  , and can also be interpreted as invertible infinite matrices which differ from the identity matrix in only finitely many places.
, and can also be interpreted as invertible infinite matrices which differ from the identity matrix in only finitely many places.It is used in algebraic K-theory
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
to define K1, and over the reals has a well-understood topology, thanks to Bott periodicity.
It should not be confused with the space of (bounded) invertible operators on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, which is a larger group, and topologically much simpler, namely contractible – see Kuiper's theorem
Kuiper's theorem
In mathematics, Kuiper's theorem is a result on the topology of operators on an infinite-dimensional, complex Hilbert space H...
.
See also
- List of finite simple groups
- SL2(R)
- Representation theory of SL2(R)Representation theory of SL2(R)In mathematics, the main results concerning irreducible unitary representations of the Lie group SL are due to Gelfand and Naimark , V...
External links
- "GL(2,p) and GL(3,3) Acting on Points" by Ed Pegg, Jr.Ed Pegg, Jr.Ed Pegg, Jr. is an expert on mathematical puzzles and is a self-described recreational mathematician. He creates puzzles for the Mathematical Association of America online at Ed Pegg, Jr.'s Math Games. His puzzles have also been used by Will Shortz on the puzzle segment of NPR's Weekend Edition...
, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
, 2007.