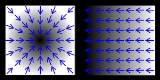
Gradient
Encyclopedia
In vector calculus, the gradient of a scalar field
is a vector field
that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude
is the greatest rate of change.
A generalization of the gradient for functions on a Euclidean space
that have values in another Euclidean space is the Jacobian. A further generalization for a function from one Banach space
to another is the Fréchet derivative
.
 , so at each point
, so at each point 
the temperature is . (We will assume that the temperature does not change over time.) At each point in the room, the gradient of
. (We will assume that the temperature does not change over time.) At each point in the room, the gradient of  at that point will show the direction the temperature rises most quickly. The magnitude of the gradient will determine how fast the temperature rises in that direction.
at that point will show the direction the temperature rises most quickly. The magnitude of the gradient will determine how fast the temperature rises in that direction.
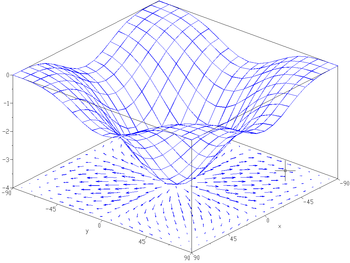
Consider a surface whose height above sea level at a point is
is  . The gradient of
. The gradient of  at a point is a vector pointing in the direction of the steepest slope
at a point is a vector pointing in the direction of the steepest slope
or grade at that point. The steepness of the slope at that point is given by the magnitude of the gradient vector.
The gradient can also be used to measure how a scalar field changes in other directions, rather than just the direction of greatest change, by taking a dot product
. Suppose that the steepest slope on a hill is 40%. If a road goes directly up the hill, then the steepest slope on the road will also be 40%. If, instead, the road goes around the hill at an angle, then it will have a shallower slope. For example, if the angle between the road and the uphill direction, projected onto the horizontal plane, is 60°, then the steepest slope along the road will be 20%, which is 40% times the cosine of 60°.
This observation can be mathematically stated as follows. If the hill height function is differentiable
is differentiable
, then the gradient of dotted
dotted
with a unit vector gives the slope of the hill in the direction of the vector. More precisely, when is differentiable, the dot product of the gradient of
is differentiable, the dot product of the gradient of  with a given unit vector is equal to the directional derivative
with a given unit vector is equal to the directional derivative
of in the direction of that unit vector.
in the direction of that unit vector.
 The gradient (or gradient vector field) of a scalar function
The gradient (or gradient vector field) of a scalar function  is denoted
is denoted  or
or  where
where  (the nabla symbol
(the nabla symbol
) denotes the vector differential operator
, del
. The notation is also used for the gradient. The gradient of f is defined to be the vector field
is also used for the gradient. The gradient of f is defined to be the vector field
whose components are the partial derivative
s of . That is:
. That is:
Here the gradient is written as a row vector, but it is often taken to be a column vector. When a function also depends on a parameter such as time, the gradient often refers simply to the vector of its spatial derivatives only.
The gradient of a vector is
is

or the Jacobian matrix
 .
.
More generally, the gradient may be defined using the exterior derivative
:

Here and
and  are the musical isomorphism
are the musical isomorphism
s.

which is often written using the standard unit vectors as
as

is:

See Del in cylindrical and spherical coordinates
.
 from the Euclidean space
from the Euclidean space
 to
to  at any particular point x0 in
at any particular point x0 in  characterizes the best linear approximation
characterizes the best linear approximation
to f at x0. The approximation is as follows:

for close to
close to  , where
, where  is the gradient of f computed at
is the gradient of f computed at  , and the dot denotes the dot product
, and the dot denotes the dot product
on . This equation is equivalent to the first two terms in the multi-variable Taylor Series
. This equation is equivalent to the first two terms in the multi-variable Taylor Series
expansion of f at x0.
 at a point
at a point  in
in  is a linear map from
is a linear map from  to
to  which is often denoted by
which is often denoted by  or
or  and called the differential
and called the differential
or (total) derivative
of at
at  . The gradient is therefore related to the differential by the formula
. The gradient is therefore related to the differential by the formula

for any . The function
. The function  , which maps
, which maps  to
to  , is called the differential or exterior derivative
, is called the differential or exterior derivative
of and is an example of a differential 1-form.
and is an example of a differential 1-form.
If is viewed as the space of (length
is viewed as the space of (length  ) column vectors (of real numbers), then one can regard
) column vectors (of real numbers), then one can regard  as the row vector
as the row vector
so that is given by matrix multiplication. The gradient is then the corresponding column vector, i.e.,
is given by matrix multiplication. The gradient is then the corresponding column vector, i.e.,  .
.
in Rn. If the function f:U → R is differentiable
, then the differential of f is the (Fréchet) derivative
of f. Thus is a function from U to the space R such that
is a function from U to the space R such that
where • is the dot product.
As a consequence, the usual properties of the derivative hold for the gradient:
Linearity
The gradient is linear in the sense that if f and g are two real-valued functions differentiable at the point a∈Rn, and α and β are two constants, then αf+βg is differentiable at a, and moreover
Product rule
If f and g are real-valued functions differentiable at a point a∈Rn, then the product rule
asserts that the product (fg)(x) = f(x)g(x) of the functions f and g is differentiable at a, and
Chain rule
Suppose that f:A→R is a real-valued function defined on a subset A of Rn, and that f is differentiable at a point a. There are two forms of the chain rule applying to the gradient. First, suppose that the function g is a parametric curve; that is, a function g : I → Rn maps a subset I ⊂ R into Rn. If g is differentiable at a point c ∈ I such that g(c) = a, then

where is the composition operator
is the composition operator
.
More generally, if instead I⊂Rk, then the following holds:

where (Dg)T denotes the transpose Jacobian matrix.
For the second form of the chain rule, suppose that h : I → R is a real valued function on a subset I of R, and that h is differentiable at the point c = f(a) ∈ I. Then
to the coordinates. This is true in the sense that if A is an orthogonal matrix, then

which follows by the chain rule above. A vector transforming in this way is known as a contravariant vector, and so the gradient is a special type of tensor
.
The differential is more natural than the gradient because it is invariant under all coordinate transformations (or diffeomorphism
s), whereas the gradient is only invariant under orthogonal transformations (because of the implicit use of the dot product in its definition). Because of this, it is common to blur the distinction between the two concepts using the notion of covariant and contravariant vectors. From this point of view, the components of the gradient transform covariantly under changes of coordinates, so it is called a covariant vector field, whereas the components of a vector field in the usual sense transform contravariantly. In this language the gradient is the differential, as a covariant vector field is the same thing as a differential 1-form.
 of the gradient at a point x with a vector v gives the directional derivative
of the gradient at a point x with a vector v gives the directional derivative
of f at x in the direction v. It follows that in this case the gradient of f is orthogonal to the level set
s of f. For example, a level surface in three-dimensional space is defined by an equation of the form F(x, y, z) = c. The gradient of F is then normal to the surface.
More generally, any embedded hypersurface
in a Riemannian manifold can be cut out by an equation of the form F(P) = 0 such that dF is nowhere zero. The gradient of F is then normal to the hypersurface.
Let us consider a function f at a point P. If we draw a surface through this point P and the function has the same value at all points on this surface,then this surface is called a 'level surface'.
along any path depends only on the endpoints of the path, and can be evaluated by the gradient theorem
(the fundamental theorem of calculus for line integrals). Conversely, a (continuous) conservative vector field is always the gradient of a function.
(M,g), the gradient of f is the vector field
 such that for any vector field
such that for any vector field  ,
,
where denotes the inner product of tangent vectors at x defined by the metric g and
denotes the inner product of tangent vectors at x defined by the metric g and
 (sometimes denoted X(f)) is the function that takes any point x∈M to the directional derivative
(sometimes denoted X(f)) is the function that takes any point x∈M to the directional derivative
of f in the direction X, evaluated at x. In other words, in a coordinate chart from an open subset of M to an open subset of Rn,
from an open subset of M to an open subset of Rn,  is given by:
is given by:
where Xj denotes the jth component of X in this coordinate chart.
So, the local form of the gradient takes the form:

Generalizing the case M=Rn, the gradient of a function is related to its exterior derivative
, since . More precisely, the gradient
. More precisely, the gradient  is the vector field associated to the differential 1-form df using the musical isomorphism
is the vector field associated to the differential 1-form df using the musical isomorphism
 (called "sharp") defined by the metric g. The relation between the exterior derivative and the gradient of a function on Rn is a special case of this in which the metric is the flat metric given by the dot product.
(called "sharp") defined by the metric g. The relation between the exterior derivative and the gradient of a function on Rn is a special case of this in which the metric is the flat metric given by the dot product.

where is the azimuthal angle,
is the azimuthal angle,  is the axial coordinate, and eρ, eφ and ez are unit vectors pointing along the coordinate directions.
is the axial coordinate, and eρ, eφ and ez are unit vectors pointing along the coordinate directions.
In spherical coordinates :

where is the azimuth angle and
is the azimuth angle and  is the zenith angle.
is the zenith angle.
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
is a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
is the greatest rate of change.
A generalization of the gradient for functions on a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
that have values in another Euclidean space is the Jacobian. A further generalization for a function from one Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
to another is the Fréchet derivative
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
.

Interpretations
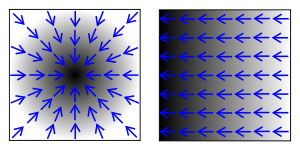
Consider a room in which the temperature is given by a scalar field, , so at each point
, so at each point 
the temperature is
 . (We will assume that the temperature does not change over time.) At each point in the room, the gradient of
. (We will assume that the temperature does not change over time.) At each point in the room, the gradient of  at that point will show the direction the temperature rises most quickly. The magnitude of the gradient will determine how fast the temperature rises in that direction.
at that point will show the direction the temperature rises most quickly. The magnitude of the gradient will determine how fast the temperature rises in that direction.Consider a surface whose height above sea level at a point
 is
is  . The gradient of
. The gradient of  at a point is a vector pointing in the direction of the steepest slope
at a point is a vector pointing in the direction of the steepest slopeSlope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
or grade at that point. The steepness of the slope at that point is given by the magnitude of the gradient vector.
The gradient can also be used to measure how a scalar field changes in other directions, rather than just the direction of greatest change, by taking a dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
. Suppose that the steepest slope on a hill is 40%. If a road goes directly up the hill, then the steepest slope on the road will also be 40%. If, instead, the road goes around the hill at an angle, then it will have a shallower slope. For example, if the angle between the road and the uphill direction, projected onto the horizontal plane, is 60°, then the steepest slope along the road will be 20%, which is 40% times the cosine of 60°.
This observation can be mathematically stated as follows. If the hill height function
 is differentiable
is differentiableDifferentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
, then the gradient of
 dotted
dottedDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
with a unit vector gives the slope of the hill in the direction of the vector. More precisely, when
 is differentiable, the dot product of the gradient of
is differentiable, the dot product of the gradient of  with a given unit vector is equal to the directional derivative
with a given unit vector is equal to the directional derivativeDirectional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
of
 in the direction of that unit vector.
in the direction of that unit vector.Definition

 is denoted
is denoted  or
or  where
where  (the nabla symbol
(the nabla symbolNabla symbol
right|thumb|256px|The [[harp]], the instrument after which the nabla symbol is namedNabla is the symbol \nabla . The name comes from the Greek word for a Hebrew harp, which had a similar shape. Related words also exist in Aramaic and Hebrew. The symbol was first used by William Rowan Hamilton in...
) denotes the vector differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
, del
Del
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
. The notation
 is also used for the gradient. The gradient of f is defined to be the vector field
is also used for the gradient. The gradient of f is defined to be the vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
whose components are the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of
 . That is:
. That is:
Here the gradient is written as a row vector, but it is often taken to be a column vector. When a function also depends on a parameter such as time, the gradient often refers simply to the vector of its spatial derivatives only.
The gradient of a vector
 is
is
or the Jacobian matrix
 .
.More generally, the gradient may be defined using the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
:

Here
 and
and  are the musical isomorphism
are the musical isomorphismMusical isomorphism
In mathematics, the musical isomorphism is an isomorphism between the tangent bundle TM and the cotangent bundle T*M of a Riemannian manifold given by its metric. There are similar isomorphisms on symplectic manifolds....
s.
Expression in 3-dimensional rectangular coordinates
The form of the gradient depends on the coordinate system used. In Cartesian coordinates, the above expression expands to
which is often written using the standard unit vectors
 as
as
Example
For example, the gradient of the function in Cartesian coordinatesis:

Expression in 3-dimensional spherical polar coordinates

See Del in cylindrical and spherical coordinates
Del in cylindrical and spherical coordinates
This is a list of some vector calculus formulae of general use in working with various curvilinear coordinate systems.- Note :* This page uses standard physics notation. For spherical coordinates, \theta is the angle between the z axis and the radius vector connecting the origin to the point in...
.
Linear approximation to a function
The gradient of a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
 from the Euclidean space
from the Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
 to
to  at any particular point x0 in
at any particular point x0 in  characterizes the best linear approximation
characterizes the best linear approximationLinear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
to f at x0. The approximation is as follows:

for
 close to
close to  , where
, where  is the gradient of f computed at
is the gradient of f computed at  , and the dot denotes the dot product
, and the dot denotes the dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
on
 . This equation is equivalent to the first two terms in the multi-variable Taylor Series
. This equation is equivalent to the first two terms in the multi-variable Taylor SeriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion of f at x0.
Differential or (exterior) derivative
The best linear approximation to a function at a point
at a point  in
in  is a linear map from
is a linear map from  to
to  which is often denoted by
which is often denoted by  or
or  and called the differential
and called the differentialDifferential (calculus)
In calculus, a differential is traditionally an infinitesimally small change in a variable. For example, if x is a variable, then a change in the value of x is often denoted Δx . The differential dx represents such a change, but is infinitely small...
or (total) derivative
Total derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
of
 at
at  . The gradient is therefore related to the differential by the formula
. The gradient is therefore related to the differential by the formula
for any
 . The function
. The function  , which maps
, which maps  to
to  , is called the differential or exterior derivative
, is called the differential or exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of
 and is an example of a differential 1-form.
and is an example of a differential 1-form.If
 is viewed as the space of (length
is viewed as the space of (length  ) column vectors (of real numbers), then one can regard
) column vectors (of real numbers), then one can regard  as the row vector
as the row vector
so that
 is given by matrix multiplication. The gradient is then the corresponding column vector, i.e.,
is given by matrix multiplication. The gradient is then the corresponding column vector, i.e.,  .
.Gradient as a derivative
Let U be an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in Rn. If the function f:U → R is differentiable
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
, then the differential of f is the (Fréchet) derivative
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
of f. Thus
 is a function from U to the space R such that
is a function from U to the space R such that
where • is the dot product.
As a consequence, the usual properties of the derivative hold for the gradient:
Linearity
The gradient is linear in the sense that if f and g are two real-valued functions differentiable at the point a∈Rn, and α and β are two constants, then αf+βg is differentiable at a, and moreover
Product rule
If f and g are real-valued functions differentiable at a point a∈Rn, then the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
asserts that the product (fg)(x) = f(x)g(x) of the functions f and g is differentiable at a, and

Chain rule
Suppose that f:A→R is a real-valued function defined on a subset A of Rn, and that f is differentiable at a point a. There are two forms of the chain rule applying to the gradient. First, suppose that the function g is a parametric curve; that is, a function g : I → Rn maps a subset I ⊂ R into Rn. If g is differentiable at a point c ∈ I such that g(c) = a, then

where
 is the composition operator
is the composition operatorComposition operator
In mathematics, the composition operator C_\phi with symbol \phi is a linear operator defined by the ruleC_\phi = f \circ\phiwhere f \circ\phi denotes function composition. In physics, and especially the area of dynamical systems, the composition operator is usually referred to as the Koopman...
.
More generally, if instead I⊂Rk, then the following holds:

where (Dg)T denotes the transpose Jacobian matrix.
For the second form of the chain rule, suppose that h : I → R is a real valued function on a subset I of R, and that h is differentiable at the point c = f(a) ∈ I. Then

Transformation properties
Although the gradient is defined in term of coordinates, it is contravariant under the application of an orthogonal matrixOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
to the coordinates. This is true in the sense that if A is an orthogonal matrix, then

which follows by the chain rule above. A vector transforming in this way is known as a contravariant vector, and so the gradient is a special type of tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
.
The differential is more natural than the gradient because it is invariant under all coordinate transformations (or diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s), whereas the gradient is only invariant under orthogonal transformations (because of the implicit use of the dot product in its definition). Because of this, it is common to blur the distinction between the two concepts using the notion of covariant and contravariant vectors. From this point of view, the components of the gradient transform covariantly under changes of coordinates, so it is called a covariant vector field, whereas the components of a vector field in the usual sense transform contravariantly. In this language the gradient is the differential, as a covariant vector field is the same thing as a differential 1-form.
Level sets
If the partial derivatives of f are continuous, then the dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
 of the gradient at a point x with a vector v gives the directional derivative
of the gradient at a point x with a vector v gives the directional derivativeDirectional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
of f at x in the direction v. It follows that in this case the gradient of f is orthogonal to the level set
Level set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
s of f. For example, a level surface in three-dimensional space is defined by an equation of the form F(x, y, z) = c. The gradient of F is then normal to the surface.
More generally, any embedded hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
in a Riemannian manifold can be cut out by an equation of the form F(P) = 0 such that dF is nowhere zero. The gradient of F is then normal to the hypersurface.
Let us consider a function f at a point P. If we draw a surface through this point P and the function has the same value at all points on this surface,then this surface is called a 'level surface'.
Conservative vector fields
The gradient of a function is called a gradient field. A (continuous) gradient field is always a conservative vector field: its line integralLine integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
along any path depends only on the endpoints of the path, and can be evaluated by the gradient theorem
Gradient theorem
The gradient theorem, also known as the fundamental theorem of calculus for line integrals, says that a line integral through a gradient field can be evaluated by evaluating the original scalar field at the endpoints of the curve: \phi\left-\phi\left = \int_L...
(the fundamental theorem of calculus for line integrals). Conversely, a (continuous) conservative vector field is always the gradient of a function.
Riemannian manifolds
For any smooth function f on a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
(M,g), the gradient of f is the vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
 such that for any vector field
such that for any vector field  ,
,
where
 denotes the inner product of tangent vectors at x defined by the metric g and
denotes the inner product of tangent vectors at x defined by the metric g and (sometimes denoted X(f)) is the function that takes any point x∈M to the directional derivative
(sometimes denoted X(f)) is the function that takes any point x∈M to the directional derivativeDirectional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
of f in the direction X, evaluated at x. In other words, in a coordinate chart
 from an open subset of M to an open subset of Rn,
from an open subset of M to an open subset of Rn,  is given by:
is given by:
where Xj denotes the jth component of X in this coordinate chart.
So, the local form of the gradient takes the form:

Generalizing the case M=Rn, the gradient of a function is related to its exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
, since
 . More precisely, the gradient
. More precisely, the gradient  is the vector field associated to the differential 1-form df using the musical isomorphism
is the vector field associated to the differential 1-form df using the musical isomorphismMusical isomorphism
In mathematics, the musical isomorphism is an isomorphism between the tangent bundle TM and the cotangent bundle T*M of a Riemannian manifold given by its metric. There are similar isomorphisms on symplectic manifolds....
 (called "sharp") defined by the metric g. The relation between the exterior derivative and the gradient of a function on Rn is a special case of this in which the metric is the flat metric given by the dot product.
(called "sharp") defined by the metric g. The relation between the exterior derivative and the gradient of a function on Rn is a special case of this in which the metric is the flat metric given by the dot product.Non-cartesian coordinate systems
In cylindrical coordinates, the gradient is given by :
where
 is the azimuthal angle,
is the azimuthal angle,  is the axial coordinate, and eρ, eφ and ez are unit vectors pointing along the coordinate directions.
is the axial coordinate, and eρ, eφ and ez are unit vectors pointing along the coordinate directions.In spherical coordinates :

where
 is the azimuth angle and
is the azimuth angle and  is the zenith angle.
is the zenith angle.External links
- Khan AcademyKhan AcademyThe Khan Academy is a not-for-profit educational organization, created in 2006 by Bangladeshi American educator Salman Khan, a graduate of MIT. With the stated mission of "providing a high quality education to anyone, anywhere", the website supplies a free online collection of more than 2,700 micro...
Gradient lesson 1




