
Locally connected space
Encyclopedia
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and other branches of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is
locally connected if every point admits a neighbourhood basis consisting entirely of open, connected sets.
Background
Throughout the history of topology, connectednessConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
and compactness
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
have been two of the most
widely studied topological properties. Indeed, the study of these properties even among subsets of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, and the recognition of their independence from the particular form of the Euclidean metric, played a large role in clarifying the notion of a topological property and thus a topological space. However, whereas the structure of compact subsets of Euclidean space was understood quite early on via the Heine–Borel theorem
Heine–Borel theorem
In the topology of metric spaces the Heine–Borel theorem, named after Eduard Heine and Émile Borel, states:For a subset S of Euclidean space Rn, the following two statements are equivalent:*S is closed and bounded...
, connected subsets of
 (for n > 1) proved to be much more complicated. Indeed, while any compact Hausdorff space
(for n > 1) proved to be much more complicated. Indeed, while any compact Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
is locally compact, a connected space – and even a connected subset of the Euclidean plane – need not be locally connected (see below).
This led to a rich vein of research in the first half of the twentieth century, in which topologists studied the implications between increasingly subtle and complex variations on the notion of a locally connected space. As an example, the notion of weak local connectedness at a point and its relation to local connectedness will be considered later on in the article.
In the latter part of the twentieth century, research trends shifted to more intense study of spaces like manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s which are locally well understood (being locally homeomorphic to Euclidean space) but have complicated global behavior. By this it is meant that although the basic point-set topology of manifolds is relatively simple (as manifolds are essentially metrizable according to most definitions of the concept), their algebraic topology is far more complex. From this modern perspective, the stronger property of local path connectedness turns out to be more important: for instance, in order for a space to admit a universal cover it must be connected and locally path connected. Local path connectedness will be discussed as well.
A space is locally connected if and only if for every open set U, the connected components of U (in the subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
) are open. It follows, for instance, that a continuous function from a locally connected space to a totally disconnected space must be locally constant. In fact the openness of components is so natural that one must be sure to keep in mind that it is not true in general: for instance Cantor space
Cantor space
In mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is homeomorphic to the Cantor set. In set theory, the topological space 2ω is called "the" Cantor space...
is totally disconnected but not discrete
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
.
Definitions and first examples
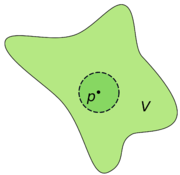
Let X be a topological space, and let x be a point of X.
We say that X is locally connected at x if for every open set V containing x there exists a connected, open set U with
 . The space X is said to be locally connected if it is locally connected at x for all x in X.
. The space X is said to be locally connected if it is locally connected at x for all x in X.By contrast, we say that X is weakly locally connected at x (or connected im kleinen at x) if for every open set V containing x there exists a connected subset N of V such that x lies in the interior of N. An equivalent definition is: each open set V containing x contains an open neighborhood U of x such that any two points in U lie in some connected subset of V. The space X is said to be weakly locally connected if it is weakly locally connected at x for all x in X.
In other words, the only difference between the two definitions is that for local connectedness at x we require a neighborhood base of open connected sets, whereas for weak local connectedness at x we require only a base of neighborhoods of x.
Evidently a space which is locally connected at x is weakly locally connected at x. The converse does not hold (a counterexample, the broom space, is given below). On the other hand, it is equally clear that a locally connected space is weakly locally connected, and here it turns out that the converse does hold: a space which is weakly locally connected at all of its points is necessarily locally connected at all of its points. A proof is given below.
We say that X is locally path connected at x if for every open set V containing x there exists a path connected, open set U with
 . The space X is said to be locally path connected if it is locally path connected at x for all x in X.
. The space X is said to be locally path connected if it is locally path connected at x for all x in X.Since path connected spaces are connected, locally path connected spaces are locally connected. This time the converse does not hold (see example 6 below).
First examples
1. For any positive integer n, the Euclidean space
 is connected and locally connected.
is connected and locally connected.2. The subspace
 of the real line
of the real line  is locally connected but not connected.
is locally connected but not connected.3. The topologist's sine curve
Topologist's sine curve
In the branch of mathematics known as topology, the topologist's sine curve is a topological space with several interesting properties that make it an important textbook example....
is a subspace of the Euclidean plane which is connected, but not locally connected.
4. The space
 of rational numbers endowed with the standard Euclidean topology, is neither connected nor locally connected.
of rational numbers endowed with the standard Euclidean topology, is neither connected nor locally connected.5. The comb space
Comb space
In mathematics, particularly topology, a comb space is a subspace of \R^2 that looks rather like a comb. The comb space has some rather interesting properties and provides interesting counterexamples. The topologist's sine curve has similar properties to the comb space...
is path connected but not locally path connected.
6. Let X be a countably infinite set endowed with the cofinite topology. Then X is locally connected (indeed, hyperconnected) but not locally path connected.
Further examples are given later on in the article.
Properties
1. Local connectedness is, by definition, a local propertyLocal property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
of topological spaces, i.e., a
topological property P such that a space X possesses property P if and only if each point x in X admits a neighborhood base of sets which have property P.
Accordingly, all the "metaproperties" held by a local property hold for local connectedness.
In particular:
2. A space is locally connected if and only if it admits a base of connected subsets.
3. The disjoint union
Disjoint union (topology)
In general topology and related areas of mathematics, the disjoint union of a family of topological spaces is a space formed by equipping the disjoint union of the underlying sets with a natural topology called the disjoint union topology...
 of a family
of a family  of spaces is locally connected if and only if each
of spaces is locally connected if and only if each  is locally connected. In particular, since a single point is certainly locally connected, it follows that any discrete space
is locally connected. In particular, since a single point is certainly locally connected, it follows that any discrete spaceDiscrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
is locally connected. On the other hand, a discrete space is totally disconnected, so is connected only if it has at most one point.
4. Conversely, a totally disconnected space
Totally disconnected space
In topology and related branches of mathematics, a totally disconnected space is a topological space that is maximally disconnected, in the sense that it has no non-trivial connected subsets...
is locally connected if and only if it is discrete. This can be used to explain the aforementioned fact that the rational numbers are not locally connected.
Components and path components
The following result follows almost immediately from the definitions but will be quite useful:Lemma: Let X be a space, and
 a family of subsets of X. Suppose that
a family of subsets of X. Suppose that  is nonempty. Then, if each
is nonempty. Then, if each  is connected (respectively, path connected) then the union
is connected (respectively, path connected) then the union  is connected (respectively, path connected).
is connected (respectively, path connected).Now consider two relations on a topological space X: for
 , write:
, write: if there is a connected subset of X containing both x and y; and
if there is a connected subset of X containing both x and y; and if there is a path connected subset of X containing both x and y.
if there is a path connected subset of X containing both x and y.Evidently both relations are reflexive and symmetric. Moreover, if x and y are contained in a connected (respectively, path connected) subset A and y and z are
connected in a connected (respectively, path connected) subset B, then the Lemma implies
that
 is a connected (respectively, path connected) subset containing
is a connected (respectively, path connected) subset containingx, y and z. Thus each relation is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, and defines a
partition of X into equivalence classes. We consider these two partitions in turn.
For x in X, the set
 of all points y such that
of all points y such that  is called the connected component
is called the connected componentConnected component
Connected components are part of topology and graph theory, two related branches of mathematics.* For the graph-theoretic concept, see connected component .* In topology: connected component .Implementations:...
of x. The Lemma implies that
 is the unique maximal connected subset of X containing x. Since
is the unique maximal connected subset of X containing x. Sincethe closure of
 is also a connected subset containing x, it follows that
is also a connected subset containing x, it follows that  is closed.
is closed.If X has only finitely many connected components, then each component is the complement of a finite union of closed sets and therefore open. In general, the connected components need not be open, since, e.g., there exist totally disconnected spaces (i.e.,
 for all points x) which are not discrete, like Cantor space. However, the connected components of a locally connected space are also open, and thus are clopen sets. It follows that a locally connected space X is a topological disjoint union
for all points x) which are not discrete, like Cantor space. However, the connected components of a locally connected space are also open, and thus are clopen sets. It follows that a locally connected space X is a topological disjoint union  of its distinct connected components. Conversely, if for every open subset U of X, the connected components of U are open, then X admits a base of connected sets and is therefore locally connected.
of its distinct connected components. Conversely, if for every open subset U of X, the connected components of U are open, then X admits a base of connected sets and is therefore locally connected.Similarly x in X, the set
 of all points y such that
of all points y such that  is called the path component of x. As above,
is called the path component of x. As above,  is also the union of all path connected subsets of X which contain x, so by the Lemma is itself path connected. Because path connected sets are connected, we have
is also the union of all path connected subsets of X which contain x, so by the Lemma is itself path connected. Because path connected sets are connected, we have  for all x in X.
for all x in X.However the closure of a path connected set need not be path connected: for instance, the topologist's sine curve is the closure of the open subset U consisting of all points (x,y) with x > 0, and U, being homeomorphic to an interval on the real line, is certainly path connected. Moreover, the path components of the topologist's sine curve C are U, which is open but not closed, and
 , which is closed but not open.
, which is closed but not open.A space is locally path connected if and only for all open subsets U, the path components of U are open. Therefore the path components of a locally path connected space give a partition of X into pairwise disjoint open sets. It follows that an open connected subspace of a locally path connected space is necessarily path connected. Moreover, if a space is locally path connected, then it is also locally connected, so for all x in X,
 is connected and locally path connected, hence path connected, i.e.,
is connected and locally path connected, hence path connected, i.e.,  . That is, for a locally path connected space the components and path components coincide.
. That is, for a locally path connected space the components and path components coincide.Examples
1. The set I × I (where I = [0,1]) in the dictionary order topology
Order topology
In mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
has exactly one component (because it is connected) but has uncountably many path components. Indeed, any set of the form {a} × I is a path component for each a belonging to I.
2. Let f be a continuous map from R to Rℓ (R in the lower limit topology
Lower limit topology
In mathematics, the lower limit topology or right half-open interval topology is a topology defined on the set R of real numbers; it is different from the standard topology on R and has a number of interesting properties...
). Since R is connected, and the image of a connected space under a continuous map must be connected, the image of R under f must be connected. Therefore, the image of R under f must be a subset of a component of Rℓ. Since this image is nonempty, the only continuous maps from R to Rℓ, are the constant maps. In fact, any continuous map from a connected space to a totally disconnected space must be constant.
Quasicomponents
Let X be a topological space. We define a third relation on X: if there is no separation of X into sets A and B such that x is an element of A and y is an element of B. This is an equivalence relation on X and the equivalence class
if there is no separation of X into sets A and B such that x is an element of A and y is an element of B. This is an equivalence relation on X and the equivalence class  containing x is called the quasicomponent of x.
containing x is called the quasicomponent of x. can also be characterized as the intersection of all clopen subsets of X which contain x. Accordingly
can also be characterized as the intersection of all clopen subsets of X which contain x. Accordingly  is closed; in general it need not be open.
is closed; in general it need not be open.Evidently
 for all x in X. Overall we have the following containments among path components, components and quasicomponents at x:
for all x in X. Overall we have the following containments among path components, components and quasicomponents at x:
If X is locally connected, then, as above,
 is a clopen set containing x, so
is a clopen set containing x, so  and thus
and thus  . Since local path connectedness implies local connectedness, it follows that at all points x of a locally path connected space we have
. Since local path connectedness implies local connectedness, it follows that at all points x of a locally path connected space we have
Examples
1. An example of a space whose quasicomponents are not equal to its components is a countable set, X, with the discrete topology along with two points a and b such that any neighbourhood of a either contains b or all but finitely many points of X, and any neighbourhood of b either contains a or all but finitely many points of X. The point a lies in the same quasicomponent of b but not in the same component as b.
2. The Arens–Fort space is not locally connected, but nevertheless the components and
the quasicomponents coincide: indeed
 for all points x.
for all points x.More on local connectedness versus weak local connectedness
TheoremLet X be a weakly locally connected space. Then X is locally connected.
Proof
It is sufficient to show that the components of open sets is open. Let U be open in X and let C be a component of U. Let x be an element of C. Then x is an element of U so that there is a connected subspace A of X contained in U and containing a neighbourhood V of x. Since A is connected and A contains x, A must be a subset of C (the component containing x). Therefore, the neighbourhood V of x is a subset of C. Since x was arbitrary, we have shown that each x in C has a neighbourhood V contained in C. This shows that C is open relative to U. Therefore, X is locally connected.
A certain infinite union of decreasing broom spaces is an example of a space which is weakly locally connected at a particular point, but not locally connected at that point.
See also
- Comb spaceComb spaceIn mathematics, particularly topology, a comb space is a subspace of \R^2 that looks rather like a comb. The comb space has some rather interesting properties and provides interesting counterexamples. The topologist's sine curve has similar properties to the comb space...
- Connected spaceConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
- Equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
- Sorgenfrey line
- Topologist's sine curveTopologist's sine curveIn the branch of mathematics known as topology, the topologist's sine curve is a topological space with several interesting properties that make it an important textbook example....
- Totally disconnected spaceTotally disconnected spaceIn topology and related branches of mathematics, a totally disconnected space is a topological space that is maximally disconnected, in the sense that it has no non-trivial connected subsets...
- Locally simply connected spaceLocally simply connected spaceIn mathematics, a locally simply connected space is a topological space that admits a basis of simply connected sets. Every locally simply connected space is also locally path-connected and locally connected....
- Semi-locally simply connectedSemi-locally simply connectedIn mathematics, specifically algebraic topology, the phrase semi-locally simply connected refers to a certain local connectedness condition that arises in the theory of covering spaces. Roughly speaking, a topological space X is semi-locally simply connected if there is a lower bound on the sizes...
Further reading
. For Hausdorff spaces, it is shown that any continuous function from a connected locally connected space into a connected space with a dispersion point is constant.

