Polytope
Encyclopedia
In elementary geometry
, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon
is a polytope in two dimensions, a polyhedron
in three dimensions, and so on in higher dimensions (such as a polychoron
in four dimensions). Some theories further generalise the idea to include such things as unbounded polytopes (apeirotopes and tessellation
s), and abstract polytope
s.
When referring to an n-dimensional generalization, the term n-polytope is used. For example, a polygon is a 2-polytope, a polyhedron is a 3-polytope, and a polychoron is a 4-polytope.
The term was coined by the mathematician Hoppe, writing in German
, and was later introduced to English by Alicia Boole Stott
, the daughter of logician George Boole
.
s to include other objects with similar properties and aesthetic beauty.
The original approach broadly followed by Schläfli, Gossett and others begins with the 0-dimensional point as a 0-polytope (vertex
). A 1-dimensional 1-polytope (edge
) is constructed by bounding a line segment with two 0-polytopes. Then 2-polytopes (polygons) are defined as plane objects whose bounding facets (edges
) are 1-polytopes, 3-polytopes (polyhedra) are defined as solids whose facets (faces
) are 2-polytopes, and so forth.
A polytope may also be regarded as a tessellation
of some given manifold
. Convex polytopes are equivalent to tilings of the sphere, while others may be tilings of other elliptic, flat or toroid
al surfaces – see elliptic tiling and toroidal polyhedron
. Under this definition, plane tilings
and space tilings (honeycombs
) are considered to be polytopes, and are sometimes classed as apeirotopes because they have infinitely many cells; tilings of hyperbolic spaces are also included under this definition.
An alternative approach defines a polytope as a set of points that admits a simplicial decomposition
. In this definition, a polytope is the union of finitely many simplices
, with the additional property that, for any two simplices that have a nonempty intersection, their intersection is a vertex, edge, or higher dimensional face of the two. However this definition does not allow star polytopes with interior structures, and so is restricted to certain areas of mathematics.
The theory of abstract polytope
s attempts to detach polytopes from the space containing them, considering their purely combinatorial properties. This allows the definition of the term to be extended to include objects for which it is difficult to define clearly a natural underlying space, such as the 11-cell
.
An n-dimensional polytope is bounded by a number of (n−1)-dimensional facets
. These facets are themselves polytopes, whose facets are (n−2)-dimensional ridges
of the original polytope. Every ridge arises as the intersection of two facets (but the intersection of two facets need not be a ridge). Ridges are once again polytopes whose facets give rise to (n−3)-dimensional boundaries of the original polytope, and so on. These bounding sub-polytopes may be referred to as faces
, or specifically j-dimensional faces or j-faces. A 0-dimensional face is called a vertex, and consists of a single point. A 1-dimensional face is called an edge, and consists of a line segment. A 2-dimensional face consists of a polygon
, and a 3-dimensional face, sometimes called a cell, consists of a polyhedron
.
. The regular polytope
s are a class of highly-symmetrical and aesthetically-pleasing polytopes, including the Platonic solid
s, which have been studied extensively since ancient times.
. The convex polytope
s are the simplest kind of polytopes, and form the basis for different generalizations of the concept of polytopes. A convex polytope is sometimes defined as the intersection of a set of half-space
s. This definition allows a polytope to be neither bounded nor finite. Polytopes are defined in this way, e.g., in linear programming
. A polytope is bounded if there is a ball of finite radius that contains it. A polytope is said to be pointed if it contains at least one vertex. Every bounded nonempty polytope is pointed. An example of a non-pointed polytope is the set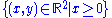
. A polytope is finite if it is defined in terms of finite number of objects, e.g., as an intersection of a finite number of half-planes.
of elements or members, which obeys certain rules. It is a purely algebraic structure, and the theory was developed in order to avoid some of the issues which make it difficult to reconcile the various geometric classes within a consistent mathematical framework. A geometric polytope is said to be a realisation of some associated abstract polytope.
In 2 dimensions, all regular polygon
s (regular 2-polytopes) are self-dual
.
In 3 dimensions, the tetrahedron
is self-dual, as well as canonical polygonal pyramids and elongated pyramids.
In higher dimensions, every regular n-simplex
, with Schlafli symbol {3n}, is self-dual.
In addition, the 24-cell in 4 dimensions, with Schlafli symbol {3,4,3}, is self-dual.
It was not until the 19th century that higher dimensions were discovered and geometers learned to construct analogues of polygons and polyhedra in them. The first hint of higher dimensions seems to have come in 1827, with Möbius
' discovery that two mirror-image solids can be superimposed by rotating one of them through a fourth dimension. By the 1850s, a handful of other mathematicians such as Cayley and Grassman had considered higher dimensions. Ludwig Schläfli
was the first of these to consider analogues of polygons and polyhedra in such higher spaces. In 1852 he described the six convex regular 4-polytope
s, but his work was not published until 1901, six years after his death. By 1854, Bernhard Riemann
's Habilitationsschrift had firmly established the geometry of higher dimensions, and thus the concept of n-dimensional polytopes was made acceptable. Schläfli's polytopes were rediscovered many times in the following decades, even during his lifetime.
In 1882 Hoppe, writing in German, coined the word polytop to refer to this more general concept of polygons and polyhedra. In due course, Alicia Boole Stott
introduced polytope into the English language.
In 1895, Thorold Gosset
not only rediscovered Schläfli's regular polytopes, but also investigated the ideas of semiregular polytopes and space-filling tessellation
s in higher dimensions. Polytopes were also studied in non-Euclidean spaces such as hyperbolic space.
During the early part of the 20th century, higher-dimensional spaces became fashionable, and together with the idea of higher polytopes, inspired artists such as Picasso to create the movement known as cubism
.
An important milestone was reached in 1948 with H. S. M. Coxeter's book Regular Polytopes
, summarising work to date and adding findings of his own. Branko Grünbaum
published his influential work on Convex Polytopes in 1967.
More recently, the concept of a polytope has been further generalized. In 1952 Shephard developed the idea of complex polytope
s in complex space, where each real dimension has an imaginary one associated with it. Coxeter went on to publish his book, Regular Complex Polytopes, in 1974. Complex polytopes do not have closed surfaces in the usual way, and are better understood as configurations
. This kind of conceptual issue led to the more general idea of incidence complexes and the study of abstract combinatorial properties relating vertices, edges, faces and so on. This in turn led to the theory of abstract polytope
s as partially-ordered sets, or posets, of such elements. McMullen and Schulte published their book Abstract Regular Polytopes in 2002.
Enumerating the uniform polytope
s, convex and nonconvex, in four or more dimensions remains an outstanding problem.
In modern times, polytopes and related concepts have found many important applications in fields as diverse as computer graphics
, optimization
, search engines, cosmology
and numerous other fields.
, linear programming
studies the maxima and minima
of linear
functions constricted to the boundary
of an
-dimensional polytope.
In linear programming
, polytopes occur in the use of Generalized barycentric coordinates and Slack variable
s.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
is a polytope in two dimensions, a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
in three dimensions, and so on in higher dimensions (such as a polychoron
Polychoron
In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
in four dimensions). Some theories further generalise the idea to include such things as unbounded polytopes (apeirotopes and tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
s), and abstract polytope
Abstract polytope
In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
s.
When referring to an n-dimensional generalization, the term n-polytope is used. For example, a polygon is a 2-polytope, a polyhedron is a 3-polytope, and a polychoron is a 4-polytope.
The term was coined by the mathematician Hoppe, writing in German
German language
German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
, and was later introduced to English by Alicia Boole Stott
Alicia Boole Stott
Alicia Boole Stott was the third daughter of George Boole and Mary Everest Boole, born in Cork, Ireland. Before marrying Walter Stott, an actuary, in 1890, she was known as Alicia Boole...
, the daughter of logician George Boole
George Boole
George Boole was an English mathematician and philosopher.As the inventor of Boolean logic—the basis of modern digital computer logic—Boole is regarded in hindsight as a founder of the field of computer science. Boole said,...
.
Different approaches to definition
The term polytope is a broad term that covers a wide class of objects, and different definitions are attested in mathematical literature. Many of these definitions are not equivalent, resulting in different sets of objects being called polytopes. They represent different approaches of generalizing the convex polytopeConvex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
s to include other objects with similar properties and aesthetic beauty.
The original approach broadly followed by Schläfli, Gossett and others begins with the 0-dimensional point as a 0-polytope (vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
). A 1-dimensional 1-polytope (edge
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
) is constructed by bounding a line segment with two 0-polytopes. Then 2-polytopes (polygons) are defined as plane objects whose bounding facets (edges
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
) are 1-polytopes, 3-polytopes (polyhedra) are defined as solids whose facets (faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
) are 2-polytopes, and so forth.
A polytope may also be regarded as a tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of some given manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. Convex polytopes are equivalent to tilings of the sphere, while others may be tilings of other elliptic, flat or toroid
Toroid
Toroid may refer to*Toroid , a doughnut-like solid whose surface is a torus.*Toroidal inductors and transformers which have wire windings on circular ring shaped magnetic cores.*Vortex ring, a toroidal flow in fluid mechanics....
al surfaces – see elliptic tiling and toroidal polyhedron
Toroidal polyhedron
In geometry, a toroidal polyhedron is a polyhedron with a genus of 1 or greater, representing topological torus surfaces.Non-self-intersecting toroidal polyhedra are embedded tori, while self-intersecting toroidal polyhedra are toroidal as abstract polyhedra, which can be verified by their Euler...
. Under this definition, plane tilings
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
and space tilings (honeycombs
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
) are considered to be polytopes, and are sometimes classed as apeirotopes because they have infinitely many cells; tilings of hyperbolic spaces are also included under this definition.
An alternative approach defines a polytope as a set of points that admits a simplicial decomposition
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
. In this definition, a polytope is the union of finitely many simplices
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
, with the additional property that, for any two simplices that have a nonempty intersection, their intersection is a vertex, edge, or higher dimensional face of the two. However this definition does not allow star polytopes with interior structures, and so is restricted to certain areas of mathematics.
The theory of abstract polytope
Abstract polytope
In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
s attempts to detach polytopes from the space containing them, considering their purely combinatorial properties. This allows the definition of the term to be extended to include objects for which it is difficult to define clearly a natural underlying space, such as the 11-cell
11-cell
In mathematics, the 11-cell is a self-dual abstract regular 4-polytope . Its 11 cells are hemi-icosahedral. It has 11 vertices, 55 edges and 55 faces. Its symmetry group is the projective special linear group L2, so it has660 symmetries...
.
Elements
The elements of a polytope are its vertices, edges, faces, cells and so on. The terminology for these is not entirely consistent across different authors. To give just a few examples: Some authors use face to refer to an (n−1)-dimensional element while others use face to denote a 2-face specifically, and others use j-face or k-face to indicate an element of j or k dimensions. Some sources use edge to refer to a ridge, while H. S. M. Coxeter uses cell to denote an (n−1)-dimensional element.An n-dimensional polytope is bounded by a number of (n−1)-dimensional facets
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
. These facets are themselves polytopes, whose facets are (n−2)-dimensional ridges
Ridge (geometry)
In geometry, a ridge is an -dimensional element of an n-dimensional polytope. It is also sometimes called a subfacet for having one lower dimension than a facet.By dimension, this corresponds to:*a vertex of a polygon;...
of the original polytope. Every ridge arises as the intersection of two facets (but the intersection of two facets need not be a ridge). Ridges are once again polytopes whose facets give rise to (n−3)-dimensional boundaries of the original polytope, and so on. These bounding sub-polytopes may be referred to as faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
, or specifically j-dimensional faces or j-faces. A 0-dimensional face is called a vertex, and consists of a single point. A 1-dimensional face is called an edge, and consists of a line segment. A 2-dimensional face consists of a polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
, and a 3-dimensional face, sometimes called a cell, consists of a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
.
| Dimension of element |
Element name (in an n-polytope) |
|---|---|
| − 1 | Null polytope (necessary in abstract Abstract polytope In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc... theory) |
| 0 | Vertex Vertex (geometry) In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:... |
| 1 | Edge Edge (geometry) In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects.... |
| 2 | Face Face (geometry) In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube... |
| 3 | Cell Cell (geometry) In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made... |
| 4 | Hypercell Hypercell In geometry, a hypercell is a descriptive term for an element of a polytope or tessellation, usually representing an element one dimension higher than a cell. The most generally accepted term is 4-face because it contains a 4-dimensional interior... |
 |
 |
| j | j-face – element of rank j = − 1, 0, 1, 2, 3, ..., n |
 |
 |
| n − 3 | Peak Peak (geometry) In geometry, a peak is an -face of an n-dimensional polytope. A peak attaches at least three facets .... – (n−3)-face |
| n − 2 | Ridge Ridge (geometry) In geometry, a ridge is an -dimensional element of an n-dimensional polytope. It is also sometimes called a subfacet for having one lower dimension than a facet.By dimension, this corresponds to:*a vertex of a polygon;... or subfacet – (n−2)-face |
| n − 1 | Facet Facet (mathematics) A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:... – (n−1)-face |
| n | Body – n-face |
Regular polytopes
A polytope may be regularRegular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
. The regular polytope
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
s are a class of highly-symmetrical and aesthetically-pleasing polytopes, including the Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s, which have been studied extensively since ancient times.
Convex polytopes
A polytope may be convexConvex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
. The convex polytope
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
s are the simplest kind of polytopes, and form the basis for different generalizations of the concept of polytopes. A convex polytope is sometimes defined as the intersection of a set of half-space
Half-space
In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
s. This definition allows a polytope to be neither bounded nor finite. Polytopes are defined in this way, e.g., in linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
. A polytope is bounded if there is a ball of finite radius that contains it. A polytope is said to be pointed if it contains at least one vertex. Every bounded nonempty polytope is pointed. An example of a non-pointed polytope is the set
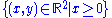. A polytope is finite if it is defined in terms of finite number of objects, e.g., as an intersection of a finite number of half-planes.Star polytopes
A non-convex polytope may be self-intersecting; this class of polytopes include the star polytopes.Abstract polytopes
An abstract polytope is a partially ordered setPartially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
of elements or members, which obeys certain rules. It is a purely algebraic structure, and the theory was developed in order to avoid some of the issues which make it difficult to reconcile the various geometric classes within a consistent mathematical framework. A geometric polytope is said to be a realisation of some associated abstract polytope.
Self-dual polytopes
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s (regular 2-polytopes) are self-dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
.
In 3 dimensions, the tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
is self-dual, as well as canonical polygonal pyramids and elongated pyramids.
In higher dimensions, every regular n-simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
, with Schlafli symbol {3n}, is self-dual.
In addition, the 24-cell in 4 dimensions, with Schlafli symbol {3,4,3}, is self-dual.
History
The concept of a polytope originally began with polygons and polyhedra, both of which have been known since ancient times:It was not until the 19th century that higher dimensions were discovered and geometers learned to construct analogues of polygons and polyhedra in them. The first hint of higher dimensions seems to have come in 1827, with Möbius
August Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
' discovery that two mirror-image solids can be superimposed by rotating one of them through a fourth dimension. By the 1850s, a handful of other mathematicians such as Cayley and Grassman had considered higher dimensions. Ludwig Schläfli
Ludwig Schläfli
Ludwig Schläfli was a Swiss geometer and complex analyst who was one of the key figures in developing the notion of higher dimensional spaces. The concept of multidimensionality has since come to play a pivotal role in physics, and is a common element in science fiction...
was the first of these to consider analogues of polygons and polyhedra in such higher spaces. In 1852 he described the six convex regular 4-polytope
Convex regular 4-polytope
In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....
s, but his work was not published until 1901, six years after his death. By 1854, Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
's Habilitationsschrift had firmly established the geometry of higher dimensions, and thus the concept of n-dimensional polytopes was made acceptable. Schläfli's polytopes were rediscovered many times in the following decades, even during his lifetime.
In 1882 Hoppe, writing in German, coined the word polytop to refer to this more general concept of polygons and polyhedra. In due course, Alicia Boole Stott
Alicia Boole Stott
Alicia Boole Stott was the third daughter of George Boole and Mary Everest Boole, born in Cork, Ireland. Before marrying Walter Stott, an actuary, in 1890, she was known as Alicia Boole...
introduced polytope into the English language.
In 1895, Thorold Gosset
Thorold Gosset
Thorold Gosset was an English lawyer and an amateur mathematician. In mathematics, he is noted for discovering and classifying the semiregular polytopes in dimensions four and higher.According to H. S. M...
not only rediscovered Schläfli's regular polytopes, but also investigated the ideas of semiregular polytopes and space-filling tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
s in higher dimensions. Polytopes were also studied in non-Euclidean spaces such as hyperbolic space.
During the early part of the 20th century, higher-dimensional spaces became fashionable, and together with the idea of higher polytopes, inspired artists such as Picasso to create the movement known as cubism
Cubism
Cubism was a 20th century avant-garde art movement, pioneered by Pablo Picasso and Georges Braque, that revolutionized European painting and sculpture, and inspired related movements in music, literature and architecture...
.
An important milestone was reached in 1948 with H. S. M. Coxeter's book Regular Polytopes
Regular Polytopes (book)
Regular Polytopes is a mathematical geometry book written by Canadian mathematician H.S.M. Coxeter. Originally written in 1947, the book was updated and republished in 1963 and 1973....
, summarising work to date and adding findings of his own. Branko Grünbaum
Branko Grünbaum
Branko Grünbaum is a Croatian-born mathematician and a professor emeritus at the University of Washington in Seattle. He received his Ph.D. in 1957 from Hebrew University of Jerusalem in Israel....
published his influential work on Convex Polytopes in 1967.
More recently, the concept of a polytope has been further generalized. In 1952 Shephard developed the idea of complex polytope
Complex polytope
A complex polytope is a generalization of a polytope in real space to an analogous structure in a complex Hilbert space, where each real dimension is accompanied by an imaginary one....
s in complex space, where each real dimension has an imaginary one associated with it. Coxeter went on to publish his book, Regular Complex Polytopes, in 1974. Complex polytopes do not have closed surfaces in the usual way, and are better understood as configurations
Configuration (geometry)
In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.Although certain specific...
. This kind of conceptual issue led to the more general idea of incidence complexes and the study of abstract combinatorial properties relating vertices, edges, faces and so on. This in turn led to the theory of abstract polytope
Abstract polytope
In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
s as partially-ordered sets, or posets, of such elements. McMullen and Schulte published their book Abstract Regular Polytopes in 2002.
Enumerating the uniform polytope
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
s, convex and nonconvex, in four or more dimensions remains an outstanding problem.
In modern times, polytopes and related concepts have found many important applications in fields as diverse as computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, search engines, cosmology
Cosmology
Cosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...
and numerous other fields.
Uses
In the study of optimizationOptimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
studies the maxima and minima
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
of linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
functions constricted to the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of an
-dimensional polytope.In linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
, polytopes occur in the use of Generalized barycentric coordinates and Slack variable
Slack variable
In an optimization problem, a slack variable is a variable that is added to an inequality constraint to transform it to an equality. Introducing a slack variable replaces an inequality constraint with an equality constraint and a nonnegativity constraint....
s.
External links
- "Math will rock your world" – application of polytopes to a database of articles used to support custom news feeds via the InternetInternetThe Internet is a global system of interconnected computer networks that use the standard Internet protocol suite to serve billions of users worldwide...
– (Business Week Online) - Regular and semi-regular convex polytopes a short historical overview: