Hausdorff space
Encyclopedia
In topology
and related branches of mathematics
, a Hausdorff space, separated space or T2 space is a topological space
in which distinct points have disjoint neighbourhoods
. Of the many separation axiom
s that can be imposed on a topological space, the "Hausdorff condition" (T2) is the most frequently used and discussed. It implies the uniqueness of limits
of sequence
s, nets, and filters. Intuitively, the condition is illustrated by the pun that a space is Hausdorff if any two points can be "housed off" from each other by open sets.
Hausdorff spaces are named for Felix Hausdorff
, one of the founders of topology. Hausdorff's original definition of a topological space (in 1914) included the Hausdorff condition as an axiom.
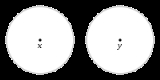
 Points x and y in a topological space X can be separated by neighbourhoods if there exists
Points x and y in a topological space X can be separated by neighbourhoods if there exists
a neighbourhood U of x and a neighbourhood V of y such that U and V are disjoint .
X is a Hausdorff space if any two distinct points of X can be separated by neighborhoods. This condition is the third separation axiom
(after T0 and T1), which is why Hausdorff spaces are also called T2 spaces. The name separated space is also used.
A related, but weaker, notion is that of a preregular space. X is a preregular space if any two topologically distinguishable points can be separated by neighbourhoods. Preregular spaces are also called R1 spaces.
The relationship between these two conditions is as follows. A topological space is Hausdorff if and only if
it is both preregular (i.e. topologically distinguishable points are separated) and Kolmogorov
(i.e. distinct points are topologically distinguishable). A topological space is preregular if and only if its Kolmogorov quotient is Hausdorff.
are Hausdorff; most importantly, the real number
s (under the standard metric topology on real numbers) are a Hausdorff space. More generally, all metric space
s are Hausdorff. In fact, many spaces of use in analysis, such as topological group
s and topological manifold
s, have the Hausdorff condition explicitly stated in their definitions.
A simple example of a topology that is T1
but is not Hausdorff is the cofinite topology defined on an infinite set.
Pseudometric space
s typically are not Hausdorff, but they are preregular, and their use in analysis is usually only in the construction of Hausdorff gauge spaces. Indeed, when analysts run across a non-Hausdorff space, it is still probably at least preregular, and then they simply replace it with its Kolmogorov quotient, which is Hausdorff.
In contrast, non-preregular spaces are encountered much more frequently in abstract algebra
and algebraic geometry
, in particular as the Zariski topology
on an algebraic variety
or the spectrum of a ring
. They also arise in the model theory
of intuitionistic logic
: every complete
Heyting algebra
is the algebra of open set
s of some topological space, but this space need not be preregular, much less Hausdorff.
While the existence of unique limits for convergent nets and filters imply that a space is Hausdorff, there are non-Hausdorff T1 spaces in which every convergent sequence has a unique limit.
of Hausdorff spaces are Hausdorff, but quotient space
s of Hausdorff spaces need not be Hausdorff. In fact, every topological space can be realized as the quotient of some Hausdorff space.
Hausdorff spaces are T1
, meaning that all singletons are closed. Similarly, preregular spaces are R0.
Another nice property of Hausdorff spaces is that compact sets are always closed. This may fail in non-Hausdorff spaces such as Sierpiński space
.
The definition of a Hausdorff space says that points can be separated by neighborhoods. It turns out that this implies something which is seemingly stronger: in a Hausdorff space every pair of disjoint compact sets can also be separated by neighborhoods, in other words there is a neighborhood of one set and a neighborhood of the other, such that the two neighborhoods are disjoint. This is an example of the general rule that compact sets often behave like points.
Compactness conditions together with preregularity often imply stronger separation axioms. For example, any locally compact
preregular space is completely regular. Compact
preregular spaces are normal
, meaning that they satisfy Urysohn's lemma
and the Tietze extension theorem and have partitions of unity subordinate to locally finite open covers. The Hausdorff versions of these statements are: every locally compact Hausdorff space is Tychonoff
, and every compact Hausdorff space is normal Hausdorff.
The following results are some technical properties regarding maps (continuous and otherwise) to and from Hausdorff spaces.
Let f : X → Y be a continuous function and suppose Y is Hausdorff. Then the graph
of f, , is a closed subset of X × Y.
, is a closed subset of X × Y.
Let f : X → Y be a function and let be its kernel
be its kernel
regarded as a subspace of X × X.
If f,g : X → Y are continuous maps and Y is Hausdorff then the equalizer is closed in X. It follows that if Y is Hausdorff and f and g agree on a dense subset of X then f = g. In other words, continuous functions into Hausdorff spaces are determined by their values on dense subsets.
is closed in X. It follows that if Y is Hausdorff and f and g agree on a dense subset of X then f = g. In other words, continuous functions into Hausdorff spaces are determined by their values on dense subsets.
Let f : X → Y be a closed surjection such that f−1(y) is compact
for all y ∈ Y. Then if X is Hausdorff so is Y.
Let f : X → Y be a quotient map with X a compact Hausdorff space. Then the following are equivalent
s are preregular, as are all Hausdorff spaces. There are many results for topological spaces that hold for both regular and Hausdorff spaces.
Most of the time, these results hold for all preregular spaces; they were listed for regular and Hausdorff spaces separately because the idea of preregular spaces came later.
On the other hand, those results that are truly about regularity generally don't also apply to nonregular Hausdorff spaces.
There are many situations where another condition of topological spaces (such as paracompactness or local compactness) will imply regularity if preregularity is satisfied.
Such conditions often come in two versions: a regular version and a Hausdorff version.
Although Hausdorff spaces aren't generally regular, a Hausdorff space that is also (say) locally compact will be regular, because any Hausdorff space is preregular.
Thus from a certain point of view, it is really preregularity, rather than regularity, that matters in these situations.
However, definitions are usually still phrased in terms of regularity, since this condition is better known than preregularity.
See History of the separation axioms
for more on this issue.
s, Cauchy space
s, and convergence spaces.
The characteristic that unites the concept in all of these examples is that limits of nets and filters (when they exist) are unique (for separated spaces) or unique up to topological indistinguishability (for preregular spaces).
As it turns out, uniform spaces, and more generally Cauchy spaces, are always preregular, so the Hausdorff condition in these cases reduces to the T0 condition.
These are also the spaces in which completeness makes sense, and Hausdorffness is a natural companion to completeness in these cases.
Specifically, a space is complete if and only if every Cauchy net has at least one limit, while a space is Hausdorff if and only if every Cauchy net has at most one limit (since only Cauchy nets can have limits in the first place).
, where one considers noncommutative C*-algebras as representing algebras of functions on a noncommutative space.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and related branches of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Hausdorff space, separated space or T2 space is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
in which distinct points have disjoint neighbourhoods
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
. Of the many separation axiom
Separation axiom
In topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms...
s that can be imposed on a topological space, the "Hausdorff condition" (T2) is the most frequently used and discussed. It implies the uniqueness of limits
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of sequence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
s, nets, and filters. Intuitively, the condition is illustrated by the pun that a space is Hausdorff if any two points can be "housed off" from each other by open sets.
Hausdorff spaces are named for Felix Hausdorff
Felix Hausdorff
Felix Hausdorff was a Jewish German mathematician who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, function theory, and functional analysis.-Life:Hausdorff studied at the University of Leipzig,...
, one of the founders of topology. Hausdorff's original definition of a topological space (in 1914) included the Hausdorff condition as an axiom.
Definitions

Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
a neighbourhood U of x and a neighbourhood V of y such that U and V are disjoint .
X is a Hausdorff space if any two distinct points of X can be separated by neighborhoods. This condition is the third separation axiom
Separation axiom
In topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms...
(after T0 and T1), which is why Hausdorff spaces are also called T2 spaces. The name separated space is also used.
A related, but weaker, notion is that of a preregular space. X is a preregular space if any two topologically distinguishable points can be separated by neighbourhoods. Preregular spaces are also called R1 spaces.
The relationship between these two conditions is as follows. A topological space is Hausdorff if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is both preregular (i.e. topologically distinguishable points are separated) and Kolmogorov
Kolmogorov space
In topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
(i.e. distinct points are topologically distinguishable). A topological space is preregular if and only if its Kolmogorov quotient is Hausdorff.
Equivalences
For a topological space X, the following are equivalent:- X is a Hausdorff space.
- Limits of nets in X are unique.
- Limits of filters on X are unique.
- Any singleton set is equal to the intersection of all closed neighbourhoodsNeighbourhood (mathematics)In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of x. (A closed neighbourhood of x is a closed setClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
that contains an open set containing x.) - The diagonal Δ = {(x,x) | x ∈ X} is closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
as a subset of the product space X × X.
Examples and counterexamples
Almost all spaces encountered in analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
are Hausdorff; most importantly, the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s (under the standard metric topology on real numbers) are a Hausdorff space. More generally, all metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s are Hausdorff. In fact, many spaces of use in analysis, such as topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s and topological manifold
Topological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
s, have the Hausdorff condition explicitly stated in their definitions.
A simple example of a topology that is T1
T1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
but is not Hausdorff is the cofinite topology defined on an infinite set.
Pseudometric space
Pseudometric space
In mathematics, a pseudometric space is a generalized metric space in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space, every seminormed space is a pseudometric space...
s typically are not Hausdorff, but they are preregular, and their use in analysis is usually only in the construction of Hausdorff gauge spaces. Indeed, when analysts run across a non-Hausdorff space, it is still probably at least preregular, and then they simply replace it with its Kolmogorov quotient, which is Hausdorff.
In contrast, non-preregular spaces are encountered much more frequently in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, in particular as the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
on an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
or the spectrum of a ring
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
. They also arise in the model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
: every complete
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
Heyting algebra
Heyting algebra
In mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
is the algebra of open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s of some topological space, but this space need not be preregular, much less Hausdorff.
While the existence of unique limits for convergent nets and filters imply that a space is Hausdorff, there are non-Hausdorff T1 spaces in which every convergent sequence has a unique limit.
Properties
Subspaces and productsProduct topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of Hausdorff spaces are Hausdorff, but quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
s of Hausdorff spaces need not be Hausdorff. In fact, every topological space can be realized as the quotient of some Hausdorff space.
Hausdorff spaces are T1
T1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
, meaning that all singletons are closed. Similarly, preregular spaces are R0.
Another nice property of Hausdorff spaces is that compact sets are always closed. This may fail in non-Hausdorff spaces such as Sierpiński space
Sierpinski space
In mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed.It is the smallest example of a topological space which is neither trivial nor discrete...
.
The definition of a Hausdorff space says that points can be separated by neighborhoods. It turns out that this implies something which is seemingly stronger: in a Hausdorff space every pair of disjoint compact sets can also be separated by neighborhoods, in other words there is a neighborhood of one set and a neighborhood of the other, such that the two neighborhoods are disjoint. This is an example of the general rule that compact sets often behave like points.
Compactness conditions together with preregularity often imply stronger separation axioms. For example, any locally compact
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
preregular space is completely regular. Compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
preregular spaces are normal
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
, meaning that they satisfy Urysohn's lemma
Urysohn's lemma
In topology, Urysohn's lemma is a lemma that states that a topological space is normal if and only if any two disjoint closed subsets can be separated by a function....
and the Tietze extension theorem and have partitions of unity subordinate to locally finite open covers. The Hausdorff versions of these statements are: every locally compact Hausdorff space is Tychonoff
Tychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
, and every compact Hausdorff space is normal Hausdorff.
The following results are some technical properties regarding maps (continuous and otherwise) to and from Hausdorff spaces.
Let f : X → Y be a continuous function and suppose Y is Hausdorff. Then the graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of f,
 , is a closed subset of X × Y.
, is a closed subset of X × Y.Let f : X → Y be a function and let
 be its kernel
be its kernelKernel of a function
In set theory, the kernel of a function f may be taken to be either*the equivalence relation on the function's domain that roughly expresses the idea of "equivalent as far as the function f can tell", or*the corresponding partition of the domain....
regarded as a subspace of X × X.
- If f is continuous and Y is Hausdorff then ker(f) is closed.
- If f is an open surjection and ker(f) is closed then Y is Hausdorff.
- If f is a continuous, open surjection (i.e. an open quotient map) then Y is Hausdorff if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
ker(f) is closed.
If f,g : X → Y are continuous maps and Y is Hausdorff then the equalizer
 is closed in X. It follows that if Y is Hausdorff and f and g agree on a dense subset of X then f = g. In other words, continuous functions into Hausdorff spaces are determined by their values on dense subsets.
is closed in X. It follows that if Y is Hausdorff and f and g agree on a dense subset of X then f = g. In other words, continuous functions into Hausdorff spaces are determined by their values on dense subsets.Let f : X → Y be a closed surjection such that f−1(y) is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
for all y ∈ Y. Then if X is Hausdorff so is Y.
Let f : X → Y be a quotient map with X a compact Hausdorff space. Then the following are equivalent
- Y is Hausdorff
- f is a closed map
- ker(f) is closed
Preregularity versus regularity
All regular spaceRegular space
In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
s are preregular, as are all Hausdorff spaces. There are many results for topological spaces that hold for both regular and Hausdorff spaces.
Most of the time, these results hold for all preregular spaces; they were listed for regular and Hausdorff spaces separately because the idea of preregular spaces came later.
On the other hand, those results that are truly about regularity generally don't also apply to nonregular Hausdorff spaces.
There are many situations where another condition of topological spaces (such as paracompactness or local compactness) will imply regularity if preregularity is satisfied.
Such conditions often come in two versions: a regular version and a Hausdorff version.
Although Hausdorff spaces aren't generally regular, a Hausdorff space that is also (say) locally compact will be regular, because any Hausdorff space is preregular.
Thus from a certain point of view, it is really preregularity, rather than regularity, that matters in these situations.
However, definitions are usually still phrased in terms of regularity, since this condition is better known than preregularity.
See History of the separation axioms
History of the separation axioms
In general topology, the separation axioms have had a convoluted history, with many competing meanings for the same term, and many competing terms for the same concept.- Origins :...
for more on this issue.
Variants
The terms "Hausdorff", "separated", and "preregular" can also be applied to such variants on topological spaces as uniform spaceUniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
s, Cauchy space
Cauchy space
In general topology and analysis, a Cauchy space is a generalization of metric spaces and uniform spaces for which the notion of Cauchy convergence still makes sense. Cauchy spaces were introduced by H. H. Keller in 1968, as an axiomatic tool derived from the idea of a Cauchy filter, in order to...
s, and convergence spaces.
The characteristic that unites the concept in all of these examples is that limits of nets and filters (when they exist) are unique (for separated spaces) or unique up to topological indistinguishability (for preregular spaces).
As it turns out, uniform spaces, and more generally Cauchy spaces, are always preregular, so the Hausdorff condition in these cases reduces to the T0 condition.
These are also the spaces in which completeness makes sense, and Hausdorffness is a natural companion to completeness in these cases.
Specifically, a space is complete if and only if every Cauchy net has at least one limit, while a space is Hausdorff if and only if every Cauchy net has at most one limit (since only Cauchy nets can have limits in the first place).
Algebra of functions
The algebra of continuous (real or complex) functions on a Hausdorff space is a commutative C*-algebra, and conversely by the Banach–Stone theorem one can recover the topology of the space from the algebraic properties of its algebra of continuous functions. This leads to noncommutative geometryNoncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
, where one considers noncommutative C*-algebras as representing algebras of functions on a noncommutative space.

