Surface
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a surface is a two-dimensional topological manifold
Topological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
R3 — for example, the surface of a ball
Ball
A ball is a round, usually spherical but sometimes ovoid, object with various uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used for simpler activities, such as catch, marbles and juggling...
. On the other hand, there are surfaces, such as the Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
, that cannot be embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
in three-dimensional Euclidean space without introducing singularities
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
or self-intersections.
To say that a surface is "two-dimensional" means that, about each point, there is a coordinate patch on which a two-dimensional coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
is defined. For example, the surface of the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
is (ideally) a two-dimensional sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, and latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
and longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
provide two-dimensional coordinates on it (except at the poles and along the 180th meridian
180th meridian
The 180th meridian or antimeridian is the meridian which is 180° east or west of the Prime Meridian passing through the Royal Observatory, Greenwich. It is common to both east longitude and west longitude. It is used as the basis for the International Date Line because it for the most part passes...
).
The concept of surface finds application in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, and many other disciplines, primarily in representing the surfaces of physical objects. For example, in analyzing the aerodynamic
Aerodynamics
Aerodynamics is a branch of dynamics concerned with studying the motion of air, particularly when it interacts with a moving object. Aerodynamics is a subfield of fluid dynamics and gas dynamics, with much theory shared between them. Aerodynamics is often used synonymously with gas dynamics, with...
properties of an airplane, the central consideration is the flow of air along its surface.
Definitions and first examples
A (topological) surface is a nonempty second countableSecond-countable space
In topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
in which every point has an open neighbourhood homeomorphic
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to some open subset
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of the Euclidean plane E2. Such a neighborhood, together with the corresponding homeomorphism, is known as a (coordinate) chart. It is through this chart that the neighborhood inherits the standard coordinates on the Euclidean plane. These coordinates are known as local coordinates and these homeomorphisms lead us to describe surfaces as being locally Euclidean.
More generally, a (topological) surface with boundary is a Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
in which every point has an open neighbourhood homeomorphic
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to some open subset
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of the upper half-plane H2. These homeomorphisms are also known as (coordinate) charts. The boundary of the upper half-plane is the x-axis. A point on the surface mapped via a chart to the x-axis is termed a boundary point. The collection of such points is known as the boundary of the surface which is necessarily a one-manifold, that is, the union of closed curves. On the other hand, a point mapped to above the x-axis is an interior point. The collection of interior points is the interior of the surface which is always non-empty
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
. The closed disk
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
is a simple example of a surface with boundary. The boundary of the disc is a circle.
The term surface used without qualification refers to surfaces without boundary. In particular, a surface with empty boundary is a surface in the usual sense. A surface with empty boundary which is compact is known as a 'closed' surface. The two-dimensional sphere, the two-dimensional torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, and the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
are examples of closed surfaces.
The Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
is a surface with only one "side". In general, a surface is said to be orientable if it does not contain a homeomorphic copy of the Möbius strip; intuitively, it has two distinct "sides". For example, the sphere and torus are orientable, while the real projective plane is not (because deleting a point or disk from the real projective plane produces the Möbius strip).
In differential and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, extra structure is added upon the topology of the surface. This added structures detects singularities
Singular point of an algebraic variety
In mathematics, a singular point of an algebraic variety V is a point P that is 'special' , in the geometric sense that V is not locally flat there. In the case of an algebraic curve, a plane curve that has a double point, such as the cubic curveexhibits at , cannot simply be parametrized near the...
, such as self-intersections and cusps, that cannot be described solely in terms of the underlying topology.
Extrinsically defined surfaces and embeddings

Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of zeros of certain functions, usually polynomial functions. Such a definition considered the surface as part of a larger (Euclidean) space, and as such was termed extrinsic.
In the previous section, a surface is defined as a topological space with certain property, namely Hausdorff and locally Euclidean. This topological space is not considered as being a subspace of another space. In this sense, the definition given above, which is the definition that mathematicians use at present, is intrinsic.
A surface defined as intrinsic is not required to satisfy the added constraint of being a subspace of Euclidean space. It seems possible at first glance that there are surfaces defined intrinsically that are not surfaces in the extrinsic sense. However, the Whitney embedding theorem asserts that every surface can in fact be embedded homeomorphically into Euclidean space, in fact into E4. Therefore the extrinsic and intrinsic approaches turn out to be equivalent.
In fact, any compact surface that is either orientable or has a boundary can be embedded in E³; on the other hand, the real projective plane, which is compact, non-orientable and without boundary, cannot be embedded into E³ (see Gramain). Steiner surface
Steiner surface
In geometry, a branch of mathematics, the Steiner surfaces, discovered by Jakob Steiner, are mappings of the real projective plane into three-dimensional real projective space...
s, including Boy's surface
Boy's surface
In geometry, Boy's surface is an immersion of the real projective plane in 3-dimensional space found by Werner Boy in 1901...
, the Roman surface
Roman surface
The Roman surface is a self-intersecting mapping of the real projective plane into three-dimensional space, with an unusually high degree of symmetry...
and the cross-cap
Cross-cap
In mathematics, a cross-cap is a two-dimensional surface that is a model of a Möbius strip with a single self intersection. This self intersection precludes the cross-cap from being topologically equivalent to a Möbius strip...
, are immersions
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
of the real projective plane into E³. These surfaces are singular where the immersions intersect themselves.
The Alexander horned sphere
Alexander horned sphere
The Alexander horned sphere is a wild embedding of a sphere into space, discovered by . It is the particular embedding of a sphere in 3-dimensional Euclidean space obtained by the following construction, starting with a standard torus:...
is a well-known pathological
Pathological (mathematics)
In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
embedding of the two-sphere into the three-sphere.
The chosen embedding (if any) of a surface into another space is regarded as extrinsic information; it is not essential to the surface itself. For example, a torus can be embedded into E³ in the "standard" manner (that looks like a bagel
Bagel
A bagel is a bread product, traditionally shaped by hand into the form of a ring from yeasted wheat dough, roughly hand-sized, which is first boiled for a short time in water and then baked. The result is a dense, chewy, doughy interior with a browned and sometimes crisp exterior...
) or in a knotted
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
manner (see figure). The two embedded tori are homeomorphic but not isotopic; they are topologically equivalent, but their embeddings are not.
The image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of a continuous, injective function from R2 to higher-dimensional Rn is said to be a parametric surface
Parametric surface
A parametric surface is a surface in the Euclidean space R3 which is defined by a parametric equation with two parameters. Parametric representation is the most general way to specify a surface. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence...
. Such an image is so-called because the x- and y- directions of the domain R2 are 2 variables that parametrize the image. Be careful that a parametric surface need not be a topological surface. A surface of revolution
Surface of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
can be viewed as a special kind of parametric surface.
If f is a smooth function from R³ to R whose gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
is nowhere zero, Then the locus
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of zeros of f does define a surface, known as an implicit surface. If the condition of non-vanishing gradient is dropped then the zero locus may develop singularities.
Construction from polygons
Each closed surface can be constructed from an oriented polygon with an even number of sides, called a fundamental polygonFundamental polygon
In mathematics, each closed surface in the sense of geometric topology can be constructed from an even-sided oriented polygon, called a fundamental polygon, by pairwise identification of its edges....
of the surface, by pairwise identification of its edges. For example, in each polygon below, attaching the sides with matching labels (A with A, B with B), so that the arrows point in the same direction, yields the indicated surface.
Any fundamental polygon can be written symbolically as follows. Begin at any vertex, and proceed around the perimeter of the polygon in either direction until returning to the starting vertex. During this traversal, record the label on each edge in order, with an exponent of -1 if the edge points opposite to the direction of traversal. The four models above, when traversed clockwise starting at the upper left, yield
- sphere:
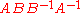
- real projective plane:

- torus:

- Klein bottle:
 .
.
Note that the sphere and the projective plane can both be realized as quotients of the 2-gon, while the torus and Klein bottle require a 4-gon (square).
The expression thus derived from a fundamental polygon of a surface turns out to be the sole relation in a presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the surface with the polygon edge labels as generators. This is a consequence of the Seifert–van Kampen theorem
Seifert–van Kampen theorem
In mathematics, the Seifert-van Kampen theorem of algebraic topology, sometimes just called van Kampen's theorem, expresses the structure of the fundamental group of a topological space X, in terms of the fundamental groups of two open, path-connected subspaces U and V that cover X...
.
Gluing edges of polygons is a special kind of quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
process. The quotient concept can be applied in greater generality to produce new or alternative constructions of surfaces. For example, the real projective plane can be obtained as the quotient of the sphere by identifying all pairs of opposite points on the sphere. Another example of a quotient is the connected sum.
Connected sums
The connected sumConnected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
of two surfaces M and N, denoted M # N, is obtained by removing a disk from each of them and gluing them along the boundary components that result. The boundary of a disk is a circle, so these boundary components are circles. The Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
 of is the sum of the Euler characteristics of the summands, minus two:
of is the sum of the Euler characteristics of the summands, minus two: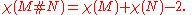
The sphere S is an identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
for the connected sum, meaning that . This is because deleting a disk from the sphere leaves a disk, which simply replaces the disk deleted from M upon gluing.
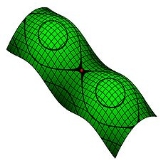
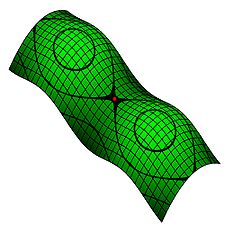
Connected summation with the torus T is also described as attaching a "handle" to the other summand M. If M is orientable, then so is . The connected sum is associative, so the connected sum of a finite collection of surfaces is well-defined.
The connected sum of two real projective planes, , is the Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
K. The connected sum of the real projective plane and the Klein bottle is homeomorphic to the connected sum of the real projective plane with the torus; in a formula, . Thus, the connected sum of three real projective planes is homeomorphic to the connected sum of the real projective plane with the torus. Any connected sum involving a real projective plane is nonorientable.
Closed surfaces
A closed surface is a surface that is compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and without boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
. Examples are spaces like the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
and the Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
. Examples of non-closed surfaces are: an open disk
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
, which is a sphere with a puncture; a cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
, which is a sphere with two punctures; and the Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
.
Classification of closed surfaces
The classification theorem of closed surfaces states that any connected closed surface is homeomorphic to some member of one of these three families:- the sphere;
- the connected sum of g tori, for
 ;
; - the connected sum of k real projective planes, for
 .
.
The surfaces in the first two families are orientable. It is convenient to combine the two families by regarding the sphere as the connected sum of 0 tori. The number g of tori involved is called the genus of the surface. The sphere and the torus have Euler characteristics 2 and 0, respectively, and in general the Euler characteristic of the connected sum of g tori is .
The surfaces in the third family are nonorientable. The Euler characteristic of the real projective plane is 1, and in general the Euler characteristic of the connected sum of k of them is .
It follows that a closed surface is determined, up to homeomorphism, by two pieces of information: its Euler characteristic, and whether it is orientable or not. In other words, Euler characteristic and orientability completely classify closed surfaces up to homeomorphism.
For closed surfaces with multiple connected component
Connected component
Connected components are part of topology and graph theory, two related branches of mathematics.* For the graph-theoretic concept, see connected component .* In topology: connected component .Implementations:...
s, they are classified by the class of each of their connected components, and thus one generally assumes that the surface is connected.
Monoid structure
Relating this classification to connected sums, the closed surfaces up to homeomorphism form a monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
with respect to the connected sum, as indeed do manifolds of any fixed dimension. The identity is the sphere, while the real projective plane and the torus generate this monoid, with a single relation , which may also be written , since . This relation is sometimes known as after Walther von Dyck
Walther von Dyck
Walther Franz Anton von Dyck , born Dyck and later ennobled, was a German mathematician...
, who proved it in , and the triple cross surface is accordingly called .
Geometrically, connect-sum with a torus adds a handle with both ends attached to the same side of the surface, while connect-sum with a Klein bottle adds a handle with the two ends attached to opposite sides of the surface; in the presence of a projective plane , the surface is not orientable (there is no notion of side), so there is no difference between attaching a torus and attaching a Klein bottle, which explains the relation.
Surfaces with boundary
Compact surfaces, possibly with boundary, are simply closed surfaces with a number of holes (open discs that have been removed); thus a connected compact surface is classified by the number of boundary components and the class of the corresponding closed surface – equivalently, by the number of boundary components, the orientability, and Euler characteristic. The genus of a compact surface is defined as the genus of the corresponding closed surface.This follows quickly but not without note from the result for closed surfaces: removing an open disc from a closed surface yields a compact surface with a circle for boundary component, and removing k open discs yields a compact surface with k disjoint circles for boundary components; the locations of the holes is irrelevant because the homeomorphism group acts k-transitively on any connected manifold of dimension at least 2.
Conversely, the boundary of a compact surface is a closed 1-manifold, which, by classification of 1-manifolds (closed curves), is a disjoint union of a finite number of circles, and these circles can be filled in (formally, taking the cone
Cone (topology)
In topology, especially algebraic topology, the cone CX of a topological space X is the quotient space:CX = /\,of the product of X with the unit interval I = [0, 1]....
), yielding a closed surface.
Compact orientable surfaces of genus g and with k boundary components are often denote as
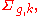 for example in the study of the mapping class group
for example in the study of the mapping class groupMapping class group
In mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
.
Riemann surfaces
A closely related example to the classification of compact 2-manifolds is the classification of compact Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s, i.e., compact complex 1-manifolds. (Note that the 2-sphere, and the tori are all complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s, in fact algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
.) Since every complex manifold is orientable, the connected sums of projective planes do not qualify. Thus compact Riemann surfaces are characterized topologically simply by their genus. The genus counts the number of holes in the manifold: the sphere has genus 0, the one-holed torus genus 1, etc.
Non-compact surfaces
Non-compact surfaces are more difficult to classify; one simple case is puncturing (removing a point, or multiple points) from a closed manifold, but even a question such as the open subsets of the plane is very complicated — for example, the complement of the Cantor setCantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
is a non-compact surface. Another example of a non-compact surface is Jacob's ladder, which looks like a ladder made of handlebodies.
Proof
The classification of closed surfaces has been known since the 1860s, and today a number of proofs exist.Topological and combinatorial proofs in general rely on the difficult result that every compact 2-manifold is homeomorphic to a simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
, which is of interest in its own right. The most common proof of the classification is , which brings every triangulated surface to a standard form. A simplified proof, which avoids a standard form, was discovered by John H. Conway circa 1992, which he called the "Zero Irrelevancy Proof" or "ZIP proof""ZIP proof" is an example of RAS syndrome
RAS syndrome
RAS syndrome , also known as PNS syndrome or RAP phrases , refers to the use of one or more of the words that make up an acronym or initialism in conjunction with the abbreviated form, thus in effect repeating one or more words...
. and is presented in .
A geometric proof, which yields a stronger geometric result, is the uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
. This was originally proven only for Riemann surfaces in the 1880s and 1900s by Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
, Paul Koebe
Paul Koebe
Paul Koebe was a 20th-century German mathematician. His work dealt exclusively with the complex numbers, his most important results being on the uniformization of Riemann surfaces in a series of four papers in 1907–1909. He did his thesis at Berlin, where he worked under Herman Schwarz...
, and Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
.
Surfaces in geometry
Polyhedra, such as the boundary of a cubeCube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
, are among the first surfaces encountered in geometry. It is also possible to define smooth surfaces, in which each point has a neighborhood diffeomorphic
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
to some open set in E². This elaboration allows calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
to be applied to surfaces to prove many results.
Two smooth surfaces are diffeomorphic if and only if they are homeomorphic. (The analogous result does not hold for higher-dimensional manifolds.) Thus closed surfaces are classified up to diffeomorphism by their Euler characteristic and orientability.
Smooth surfaces equipped with Riemannian metrics are of fundational importance in differential geometry. A Riemannian metric endows a surface with notions of geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
, distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
, angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
, and area. It also gives rise to Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
, which describes how curved or bent the surface is at each point. Curvature is a rigid, geometric property, in that it is not preserved by general diffeomorphisms of the surface. However, the famous Gauss-Bonnet theorem for closed surfaces states that the integral of the Gaussian curvature K over the entire surface S is determined by the Euler characteristic:
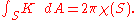
This result exemplifies the deep relationship between the geometry and topology of surfaces (and, to a lesser extent, higher-dimensional manifolds).
Another way in which surfaces arise in geometry is by passing into the complex domain. A complex one-manifold is a smooth oriented surface, also called a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
. Any complex nonsingular algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
viewed as a complex manifold is a Riemann surface.
Every closed orientable surface admits a complex structure. Complex structures on a closed oriented surface correspond to conformal equivalence classes of Riemannian metrics on the surface. One version of the uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
(due to Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
) states that any Riemannian metric on an oriented, closed surface is conformally equivalent to an essentially unique metric of constant curvature
Constant curvature
In mathematics, constant curvature in differential geometry is a concept most commonly applied to surfaces. For those the scalar curvature is a single number determining the local geometry, and its constancy has the obvious meaning that it is the same at all points...
. This provides a starting point for one of the approaches to Teichmüller theory, which provides a finer classification of Riemann surfaces than the topological one by Euler characteristic alone.
A complex surface is a complex two-manifold and thus a real four-manifold; it is not a surface in the sense of this article. Neither are algebraic curves defined over field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s other than the complex numbers,
nor are algebraic surfaces defined over field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s other than the real numbers.
See also
- Volume formVolume formIn mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
, for volumes of surfaces in En - Poincaré metricPoincaré metricIn mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
, for metric properties of Riemann surfaces - Area element, the area of a differential element of a surface
- Roman surfaceRoman surfaceThe Roman surface is a self-intersecting mapping of the real projective plane into three-dimensional space, with an unusually high degree of symmetry...
- Boy's surfaceBoy's surfaceIn geometry, Boy's surface is an immersion of the real projective plane in 3-dimensional space found by Werner Boy in 1901...
- TetrahemihexahedronTetrahemihexahedronIn geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 6 vertices and 12 edges, and 7 faces: 4 triangular and 3 square. Its vertex figure is a crossed quadrilateral. It has Coxeter-Dynkin diagram of ....
External links
- The Classification of Surfaces and the Jordan Curve Theorem in Home page of Andrew Ranicki
- Math Surfaces Gallery, with 60 ~surfaces and Java Applet for live rotation viewing
- Math Surfaces Animation, with JavaScript (Canvas HTML) for tens surfaces rotation viewing
- The Classification of Surfaces Lecture Notes by Z.Fiedorowicz
- History and Art of Surfaces and their Mathematical Models

