
Table of Lie groups
Encyclopedia
This article gives a table of some common Lie group
s and their associated Lie algebra
s.
The following are noted: the topological
properties of the group (dimension
, connectedness
, compactness
, the nature of the fundamental group
, and whether or not they are simply connected), as well as on their algebraic properties (abelian
, simple
, semisimple).
For more examples of Lie groups and other related topics see the list of simple Lie groups, the Bianchi classification
of groups of dimension at most 3, and the List of Lie group topics.
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s and their associated Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s.
The following are noted: the topological
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
properties of the group (dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
, connectedness
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, compactness
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, the nature of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
, and whether or not they are simply connected), as well as on their algebraic properties (abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
, semisimple).
For more examples of Lie groups and other related topics see the list of simple Lie groups, the Bianchi classification
Bianchi classification
In mathematics, the Bianchi classification, named for Luigi Bianchi, is a classification of the 3-dimensional real Lie algebras into 11 classes, 9 of which are single groups and two of which have a continuum of isomorphism classes...
of groups of dimension at most 3, and the List of Lie group topics.
Real Lie groups and their algebras
Column legend- CM: Is this group G compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
? (Yes or No) -
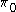 : Gives the group of components of G. The order of the component group gives the number of connected componentsConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
: Gives the group of components of G. The order of the component group gives the number of connected componentsConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
. The group is connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
if and only if the component group is trivialTrivial groupIn mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
(denoted by 0). -
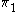 : Gives the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
: Gives the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of G whenever G is connected. The group is simply connected if and only if the fundamental group is trivialTrivial groupIn mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
(denoted by 0). - UC: If G is not simply connected, gives the universal cover of G.
| Lie group | Description | CM | 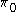 |
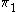 |
UC | Remarks | Lie algebra | dim/R |
|---|---|---|---|---|---|---|---|---|
| Rn | Euclidean space Euclidean space In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions... with addition |
N | 0 | 0 | abelian | Rn | n | |
| R× | nonzero real number Real number In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π... s with multiplication |
N | Z2 | – | abelian | R | 1 | |
| R+ | positive real numbers with multiplication | N | 0 | 0 | abelian | R | 1 | |
| S1 = U(1) | the circle group: complex number Complex number A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part... s of absolute value 1, with multiplication; |
Y | 0 | Z | R | abelian, isomorphic to SO(2), Spin(2), and R/Z | R | 1 |
| Aff(1) Affine group In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions.... |
invertible affine transformation Affine transformation In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property... s from R to R. |
N | Z2 | 0 | solvable Solvable group In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions... , semidirect product Semidirect product In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product... of R+ and R× |
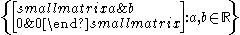 |
2 | |
| H× | non-zero quaternions with multiplication | N | 0 | 0 | H | 4 | ||
| S3 = Sp(1) | quaternions of absolute value Absolute value In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3... 1, with multiplication; topologically a 3-sphere 3-sphere In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space... |
Y | 0 | 0 | isomorphic to SU(2) and to Spin(3); double cover of SO(3) | Im(H) | 3 | |
| GL(n,R) | general linear group General linear group In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible... : invertible n×n real matrices Matrix (mathematics) In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element... |
N | Z2 | – | M(n,R) | n2 | ||
| GL+(n,R) | n×n real matrices with positive determinant Determinant In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well... |
N | 0 | Z n=2 Z2 n>2 |
GL+(1,R) is isomorphic to R+ and is simply connected | M(n,R) | n2 | |
| SL(n,R) | special linear group Special linear group In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion.... : real matrices with determinant Determinant In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well... 1 |
N | 0 | Z n=2 Z2 n>2 |
SL(1,R) is a single point and therefore compact and simply connected | sl(n,R) | n2−1 | |
| SL(2,R) | Orientation-preserving isometries of the Poincaré half-plane, isomorphic to SU(1,1), isomorphic to Sp(2,R). | N | 0 | Z | The universal cover has no finite-dimensional representations. | sl(2,R) | 3 | |
| O(n) | orthogonal group Orthogonal group In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication... : real orthogonal matrices Orthogonal matrix In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors .... |
Y | Z2 | – | The symmetry group of the sphere Sphere A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point... (n=3) or hypersphere Hypersphere In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any... . |
so(n) | n(n−1)/2 | |
| SO(n) | special orthogonal group: real orthogonal matrices with determinant 1 | Y | 0 | Z n=2 Z2 n>2 |
Spin(n) n>2 |
SO(1) is a single point and SO(2) is isomorphic to the circle group, SO(3) is the rotation group of the sphere. | so(n) | n(n−1)/2 |
| Spin(n) | spin group: double cover of SO(n) | Y | 0 n>1 | 0 n>2 | Spin(1) is isomorphic to Z2 and not connected; Spin(2) is isomorphic to the circle group and not simply connected | so(n) | n(n−1)/2 | |
| Sp(2n,R) | symplectic group Symplectic group In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually... : real symplectic matrices |
N | 0 | Z | sp(2n,R) | n(2n+1) | ||
| Sp(n) | compact symplectic group: quaternionic n×n unitary matrices | Y | 0 | 0 | sp(n) | n(2n+1) | ||
| U(n) | unitary group Unitary group In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL... : complex Complex number A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part... n×n unitary matrices |
Y | 0 | Z | R×SU(n) | For n=1: isomorphic to S1. Note: this is not a complex Lie group/algebra | u(n) | n2 |
| SU(n) | special unitary group Special unitary group The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication... : complex Complex number A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part... n×n unitary matrices with determinant 1 |
Y | 0 | 0 | Note: this is not a complex Lie group/algebra | su(n) | n2−1 | |
Real Lie algebras
Table legend:- S: Is this algebra simple? (Yes or No)
- SS: Is this algebra semi-simple? (Yes or No)
| Lie algebra | Description | S | SS | Remarks | dim/R |
|---|---|---|---|---|---|
| R | the real number Real number In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π... s, the Lie bracket is zero |
1 | |||
| Rn | the Lie bracket is zero | n | |||
| H | quaternions, with Lie bracket the commutator | 4 | |||
| Im(H) | quaternions with zero real part, with Lie bracket the commutator; isomorphic to real 3-vectors, with Lie bracket the cross product Cross product In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them... ; also isomorphic to su(2) and to so(3,R) |
Y | Y | 3 | |
| M(n,R) | n×n matrices, with Lie bracket the commutator | n2 | |||
| sl(n,R) | square matrices with trace 0, with Lie bracket the commutator | n2−1 | |||
| so(n) | skew-symmetric square real matrices, with Lie bracket the commutator. | Y | Y | Exception: so(4) is semi-simple, but not simple. | n(n−1)/2 |
| sp(2n,R) | real matrices that satisfy JA + ATJ = 0 where J is the standard skew-symmetric matrix Skew-symmetric matrix In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e... |
Y | Y | n(2n+1) | |
| sp(n) | square quaternionic matrices A satisfying A = −A*, with Lie bracket the commutator | Y | Y | n(2n+1) | |
| u(n) | square complex matrices A satisfying A = −A*, with Lie bracket the commutator | n2 | |||
| su(n) n≥2 |
square complex matrices A with trace 0 satisfying A = −A*, with Lie bracket the commutator | Y | Y | n2−1 | |
Complex Lie groups and their algebras
The dimensions given are dimensions over C. Note that every complex Lie group/algebra can also be viewed as a real Lie group/algebra of twice the dimension.| Lie group | Description | CM |  |
 |
UC | Remarks | Lie algebra | dim/C |
|---|---|---|---|---|---|---|---|---|
| Cn | group operation is addition | N | 0 | 0 | abelian | Cn | n | |
| C× | nonzero complex number Complex number A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part... s with multiplication |
N | 0 | Z | abelian | C | 1 | |
| GL(n,C) | general linear group General linear group In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible... : invertible n×n complex matrices Matrix (mathematics) In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element... |
N | 0 | Z | For n=1: isomorphic to C× | M(n,C) | n2 | |
| SL(n,C) | special linear group Special linear group In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion.... : complex matrices with determinant Determinant In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well... 1 |
N | 0 | 0 | for n=1 this is a single point and thus compact. | sl(n,C) | n2−1 | |
| SL(2,C) | Special case of SL(n,C) for n=2 | N | 0 | 0 | Isomorphic to Spin(3,C), isomorphic to Sp(2,C) | sl(2,C) | 3 | |
| PSL(2,C) | Projective special linear group | N | 0 | Z2 | SL(2,C) | Isomorphic to the Möbius group, isomorphic to the restricted Lorentz group Lorentz group In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena... SO+(3,1,R), isomorphic to SO(3,C). |
sl(2,C) | 3 |
| O(n,C) | orthogonal group Orthogonal group In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication... : complex orthogonal matrices Orthogonal matrix In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors .... |
N | Z2 | – | compact for n=1 | so(n,C) | n(n−1)/2 | |
| SO(n,C) | special orthogonal group: complex orthogonal matrices with determinant 1 | N | 0 | Z n=2 Z2 n>2 |
SO(2,C) is abelian and isomorphic to C×; nonabelian for n>2. SO(1,C) is a single point and thus compact and simply connected | so(n,C) | n(n−1)/2 | |
| Sp(2n,C) | symplectic group Symplectic group In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually... : complex symplectic matrices |
N | 0 | 0 | sp(2n,C) | n(2n+1) | ||
Complex Lie algebras
The dimensions given are dimensions over C. Note that every complex Lie algebra can also be viewed as a real Lie algebra of twice the dimension.| Lie algebra | Description | S | SS | Remarks | dim/C |
|---|---|---|---|---|---|
| C | the complex number Complex number A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part... s |
1 | |||
| Cn | the Lie bracket is zero | n | |||
| M(n,C) | n×n matrices, with Lie bracket the commutator | n2 | |||
| sl(n,C) | square matrices with trace 0, with Lie bracket the commutator |
Y | Y | n2−1 | |
| sl(2,C) | Special case of sl(n,C) with n=2 | Y | Y | isomorphic to su(2) 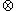 C C |
3 |
| so(n,C) | skew-symmetric square complex matrices, with Lie bracket the commutator |
Y | Y | Exception: so(4,C) is semi-simple, but not simple. | n(n−1)/2 |
| sp(2n,C) | complex matrices that satisfy JA + ATJ = 0 where J is the standard skew-symmetric matrix Skew-symmetric matrix In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e... |
Y | Y | n(2n+1) | |

