Quotient space
Overview
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and related areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
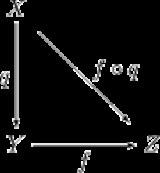
, a quotient space (also called an identification space) is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
. This is commonly done in order to construct new spaces from given ones.
Let be a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, and let ~ be an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on X. The quotient space,
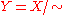 is defined to be the set of equivalence classes of elements of :
is defined to be the set of equivalence classes of elements of :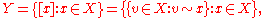
equipped with the topology where the open sets are defined to be those sets of equivalence classes whose unions are open sets in X:
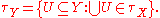
Equivalently, we can define them to be those sets with an open preimage under the quotient map
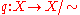 which sends a point in X to the equivalence class containing it.
which sends a point in X to the equivalence class containing it.
- Gluing. Often, topologists talk of gluing points together.

