Product topology
Encyclopedia
In topology
and related areas of mathematics
, a product space is the cartesian product
of a family of topological space
s equipped with a natural topology called the product topology. This topology differs from another, perhaps more obvious, topology called the box topology
, which can also be given to a product space and which agrees with the product topology when the product is over only finitely many spaces. However, the product topology is "correct" in that it makes the product space a categorical product
of its factors, whereas the box topology is too fine
; this is the sense in which the product topology is "natural".
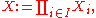
or the (possibly infinite) Cartesian product of the topological spaces Xi, indexed
by , and the canonical projections pi : X → Xi, the product topology on X is defined to be the coarsest topology (i.e. the topology with the fewest open sets) for which all the projections pi are continuous. The product topology is sometimes called the Tychonoff topology.
, and the canonical projections pi : X → Xi, the product topology on X is defined to be the coarsest topology (i.e. the topology with the fewest open sets) for which all the projections pi are continuous. The product topology is sometimes called the Tychonoff topology.
The open sets in the product topology are unions (finite or infinite) of sets of the form , where each Ui is open in Xi and Ui ≠ Xi only finitely many times.
, where each Ui is open in Xi and Ui ≠ Xi only finitely many times.
The product topology on X is the topology generated by sets of the form pi−1(U), where i in I and U is an open subset of Xi. In other words, the sets {pi−1(U)} form a subbase
for the topology on X. A subset
of X is open if and only if it is a (possibly infinite) union
of intersections
of finitely many sets of the form pi−1(U). The pi−1(U) are sometimes called open cylinders, and their intersections are cylinder set
s.
We can describe a basis for the product topology using bases of the constituting spaces Xi. A basis consists of sets , where for cofinitely many
, where for cofinitely many
(all but finitely many) i, (it's the whole space), and otherwise it's a basic open set of
(it's the whole space), and otherwise it's a basic open set of  .
.
In particular, for a finite product (in particular, for the product of two topological spaces), the products of base elements of the Xi gives a basis for the product .
.
In general, the product of the topologies of each Xi forms a basis for what is called the box topology
on X. In general, the box topology is finer than the product topology, but for finite products they coincide.
R and defines a topology on the product of n copies of R in this fashion, one obtains the ordinary Euclidean topology
on Rn.
The Cantor set
is homeomorphic to the product of countably many copies of the discrete space
{0,1} and the space of irrational number
s is homeomorphic to the product of countably many copies of the natural number
s, where again each copy carries the discrete topology.
Several additional examples are given in the article on the initial topology
.
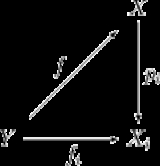
: If Y is a topological space, and for every i in I, fi : Y → Xi is a continuous map, then there exists precisely one continuous map f : Y → X such that for each i in I the following diagram commutes
:
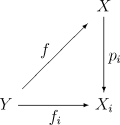 This shows that the product space is a product
This shows that the product space is a product
in the category of topological spaces
. If follows from the above universal property that a map f : Y → X is continuous if and only if
fi = pi o f is continuous for all i in I. In many cases it is often easier to check that the component functions fi are continuous. Checking whether a map g : X→ Z is continuous is usually more difficult; one tries to use the fact that the pi are continuous in some way.
In addition to being continuous, the canonical projections pi : X → Xi are open maps. This means that any open subset of the product space remains open when projected down to the Xi. The converse is not true: if W is a subspace of the product space whose projections down to all the Xi are open, then W need not be open in X. (Consider for instance W = R2 \ (0,1)2.) The canonical projections are not generally closed maps (consider for example the closed set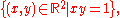 whose projections onto both axes are R \ {0}).
whose projections onto both axes are R \ {0}).
The product topology is also called the topology of pointwise convergence because of the following fact: a sequence
(or net
) in X converges if and only if all its projections to the spaces Xi converge. In particular, if one considers the space X = RI of all real
valued function
s on I, convergence in the product topology is the same as pointwise convergence of functions.
Any product of closed subsets of Xi is a closed set in X.
An important theorem about the product topology is Tychonoff's theorem
: any product of compact space
s is compact. This is easy to show for finite products, while the general statement is equivalent to the axiom of choice.
The axiom of choice occurs again in the study of (topological) product spaces; for example, Tychonoff's theorem
on compact sets is a more complex and subtle example of a statement that is equivalent to the axiom of choice.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and related areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a product space is the cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of a family of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s equipped with a natural topology called the product topology. This topology differs from another, perhaps more obvious, topology called the box topology
Box topology
In topology, the cartesian product of topological spaces can be given several different topologies. The canonical one is the product topology, because it fits rather nicely with the categorical notion of a product. Another possibility is the box topology. The box topology has a somewhat more...
, which can also be given to a product space and which agrees with the product topology when the product is over only finitely many spaces. However, the product topology is "correct" in that it makes the product space a categorical product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
of its factors, whereas the box topology is too fine
Comparison of topologies
In topology and related areas of mathematics comparison of topologies refers to the fact that two topological structures on a given set may stand in relation to each other. The set of all possible topologies on a given set forms a partially ordered set...
; this is the sense in which the product topology is "natural".
Definition
Given X such that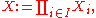
or the (possibly infinite) Cartesian product of the topological spaces Xi, indexed
Index set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
by
 , and the canonical projections pi : X → Xi, the product topology on X is defined to be the coarsest topology (i.e. the topology with the fewest open sets) for which all the projections pi are continuous. The product topology is sometimes called the Tychonoff topology.
, and the canonical projections pi : X → Xi, the product topology on X is defined to be the coarsest topology (i.e. the topology with the fewest open sets) for which all the projections pi are continuous. The product topology is sometimes called the Tychonoff topology.The open sets in the product topology are unions (finite or infinite) of sets of the form
 , where each Ui is open in Xi and Ui ≠ Xi only finitely many times.
, where each Ui is open in Xi and Ui ≠ Xi only finitely many times.The product topology on X is the topology generated by sets of the form pi−1(U), where i in I and U is an open subset of Xi. In other words, the sets {pi−1(U)} form a subbase
Subbase
In topology, a subbase for a topological space X with topology T is a subcollection B of T which generates T, in the sense that T is the smallest topology containing B...
for the topology on X. A subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of X is open if and only if it is a (possibly infinite) union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of intersections
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of finitely many sets of the form pi−1(U). The pi−1(U) are sometimes called open cylinders, and their intersections are cylinder set
Cylinder set
In mathematics, a cylinder set is the natural open set of a product topology. Cylinder sets are particularly useful in providing the base of the natural topology of the product of a countable number of copies of a set...
s.
We can describe a basis for the product topology using bases of the constituting spaces Xi. A basis consists of sets
 , where for cofinitely many
, where for cofinitely manyCofinite
In mathematics, a cofinite subset of a set X is a subset A whose complement in X is a finite set. In other words, A contains all but finitely many elements of X...
(all but finitely many) i,
 (it's the whole space), and otherwise it's a basic open set of
(it's the whole space), and otherwise it's a basic open set of  .
.In particular, for a finite product (in particular, for the product of two topological spaces), the products of base elements of the Xi gives a basis for the product
 .
.In general, the product of the topologies of each Xi forms a basis for what is called the box topology
Box topology
In topology, the cartesian product of topological spaces can be given several different topologies. The canonical one is the product topology, because it fits rather nicely with the categorical notion of a product. Another possibility is the box topology. The box topology has a somewhat more...
on X. In general, the box topology is finer than the product topology, but for finite products they coincide.
Examples
If one starts with the standard topology on the real lineReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R and defines a topology on the product of n copies of R in this fashion, one obtains the ordinary Euclidean topology
Euclidean topology
In mathematics, and especially general topology, the Euclidean topology is an example of a topology given to the set of real numbers, denoted by R...
on Rn.
The Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
is homeomorphic to the product of countably many copies of the discrete space
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
{0,1} and the space of irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s is homeomorphic to the product of countably many copies of the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, where again each copy carries the discrete topology.
Several additional examples are given in the article on the initial topology
Initial topology
In general topology and related areas of mathematics, the initial topology on a set X, with respect to a family of functions on X, is the coarsest topology on X which makes those functions continuous.The subspace topology and product topology constructions are both special cases of initial...
.
Properties
The product space X, together with the canonical projections, can be characterized by the following universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
: If Y is a topological space, and for every i in I, fi : Y → Xi is a continuous map, then there exists precisely one continuous map f : Y → X such that for each i in I the following diagram commutes
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:

Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
in the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
. If follows from the above universal property that a map f : Y → X is continuous if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
fi = pi o f is continuous for all i in I. In many cases it is often easier to check that the component functions fi are continuous. Checking whether a map g : X→ Z is continuous is usually more difficult; one tries to use the fact that the pi are continuous in some way.
In addition to being continuous, the canonical projections pi : X → Xi are open maps. This means that any open subset of the product space remains open when projected down to the Xi. The converse is not true: if W is a subspace of the product space whose projections down to all the Xi are open, then W need not be open in X. (Consider for instance W = R2 \ (0,1)2.) The canonical projections are not generally closed maps (consider for example the closed set
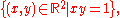 whose projections onto both axes are R \ {0}).
whose projections onto both axes are R \ {0}).The product topology is also called the topology of pointwise convergence because of the following fact: a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
(or net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
) in X converges if and only if all its projections to the spaces Xi converge. In particular, if one considers the space X = RI of all real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s on I, convergence in the product topology is the same as pointwise convergence of functions.
Any product of closed subsets of Xi is a closed set in X.
An important theorem about the product topology is Tychonoff's theorem
Tychonoff's theorem
In mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact. The theorem is named after Andrey Nikolayevich Tychonoff, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the...
: any product of compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
s is compact. This is easy to show for finite products, while the general statement is equivalent to the axiom of choice.
Relation to other topological notions
- Separation
- Every product of T0 spaces is T0
- Every product of T1 spaceT1 spaceIn topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
s is T1 - Every product of Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s is Hausdorff - Every product of regular spaceRegular spaceIn topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
s is regular - Every product of Tychonoff spaceTychonoff spaceIn topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
s is Tychonoff - A product of normal spaceNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
s need not be normal
- Compactness
- Every product of compact spaces is compact (Tychonoff's theoremTychonoff's theoremIn mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact. The theorem is named after Andrey Nikolayevich Tychonoff, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the...
) - A product of locally compact spaceLocally compact spaceIn topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
s need not be locally compact. However, an arbitrary product of locally compact spaces where all but finitely many are compact is locally compact (This condition is sufficient and necessary).
- Every product of compact spaces is compact (Tychonoff's theorem
- Connectedness
- Every product of connectedConnectednessIn mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
(resp. path-connected) spaces is connected (resp. path-connected) - Every product of hereditarily disconnected spaces is hereditarily disconnected.
- Every product of connected
Axiom of choice
The axiom of choice is equivalent to the statement that the product of a collection of non-empty sets is non-empty. The proof is easy enough: one needs only to pick an element from each set to find a representative in the product. Conversely, a representative of the product is a set which contains exactly one element from each component.The axiom of choice occurs again in the study of (topological) product spaces; for example, Tychonoff's theorem
Tychonoff's theorem
In mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact. The theorem is named after Andrey Nikolayevich Tychonoff, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the...
on compact sets is a more complex and subtle example of a statement that is equivalent to the axiom of choice.
See also
- Disjoint union (topology)Disjoint union (topology)In general topology and related areas of mathematics, the disjoint union of a family of topological spaces is a space formed by equipping the disjoint union of the underlying sets with a natural topology called the disjoint union topology...
- Projective limit topologyInitial topologyIn general topology and related areas of mathematics, the initial topology on a set X, with respect to a family of functions on X, is the coarsest topology on X which makes those functions continuous.The subspace topology and product topology constructions are both special cases of initial...
- Quotient spaceQuotient spaceIn topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
- Subspace (topology)

