Homology (mathematics)
Encyclopedia
In mathematics
(especially algebraic topology
and abstract algebra
), homology (in part from Greek
ὁμόιος homos "identical") is a certain general procedure to associate a sequence
of abelian group
s or modules
with a given mathematical object such as a topological space
or a group
. See homology theory
for more background, or singular homology
for a concrete version for topological spaces, or group cohomology
for a concrete version for groups.
For a topological space, the homology groups are generally much easier to compute than the homotopy group
s, and consequently one usually will have an easier time working with homology to aid in the classification of spaces.
The original motivation for defining homology groups is the commonplace observation that one aspect of the shape of an object is its holes. But because a hole is "not there", it is not immediately obvious how to define a hole, or how to distinguish between different kinds of holes. Homology is a rigorous mathematical method for detecting and categorizing holes in a shape. As it turns out, there exist subtle kinds of holes that homology cannot "see" — in which case homotopy groups may be what is needed.
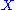, on which one first defines a chain complex
encoding information about 
. A chain complex is a sequence of abelian groups or modules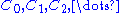 
connected by homomorphisms
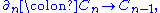which are called boundary operators. That is,
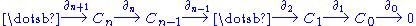
where 0 denotes the trivial group and
for 
. It is also required that the composition of any two consecutive boundary operators be trivial. That is, for all 
,
i.e., the constant map to the group identity in
. This means 
.
Now since each
is abelian, 
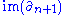is a normal subgroup of 
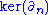. And we want to mod out by this subgroup, i.e., consider everything in 
equivalent and partition 
using this equivalence relation. The n-th homology group of X is defined to be the factor group (or quotient module
)
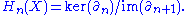
We also use the notation
and 
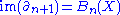, so
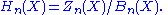
Computing these two groups is usually rather difficult since they are very large groups. On the other hand, we do have tools which make the task easier.
The simplicial homology
groups
of a simplicial complex
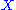are defined using the simplicial chain complex 
, with 
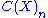the free abelian group generated by the 
-simplices of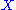 
. The singular homology
groups
are defined for any topological space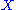 
, and agree with the simplicial homology groups for a simplicial complex.
A chain complex is said to be exact
if the image of the (n + 1)-th map is always equal to the kernel of the nth map. The homology groups of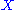
therefore measure "how far" the chain complex associated to 
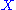is from being exact.
Cohomology groups are formally similar: one starts with a cochain complex, which is the same as a chain complex but whose arrows, now denoted
point in the direction of increasing n rather than decreasing n; then the groups 
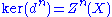and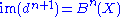 
follow from the same description and
as before.
: the simplicial homology
of a simplicial complex
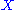. Here 
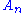is the free abelian group
or module whose generators are the n-dimensional
oriented simplexes of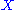
. The mappings are called the boundary mappings and send the simplex with vertices
to the sum
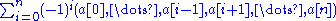
(which is considered 0 if n = 0).
If we take the modules to be over a field, then the dimension
of the n-th homology of
turns out to be the number of "holes" in 
at dimension n.
Using this example as a model, one can define a singular homology for any topological space
. We define a chain complex for 
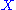by taking 
to be the free abelian group (or free module) whose generators are all continuous maps from n-dimensional simplices
into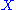
. The homomorphisms 
arise from the boundary maps of simplices.
In abstract algebra
, one uses homology to define derived functor
s, for example the Tor functor
s. Here one starts with some covariant additive functor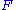
and some module 
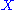. The chain complex for 
is defined as follows: first find a free module 
and a surjective homomorphism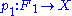 
. Then one finds a free module 
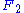and a surjective homomorphism 
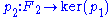. Continuing in this fashion, a sequence of free modules 
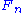and homomorphisms 
can be defined. By applying the functor 
to this sequence, one obtains a chain complex; the homology 
of this complex depends only on 
and 
and is, by definition, the n-th derived functor of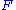 
, applied to 
.
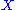: A morphism from the chain complex
to the chain complex 
is a sequence of homomorphisms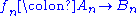 
such that 
for all n. The n-th homology Hn can be viewed as a covariant functor
from the category of chain complexes to the category of abelian groups (or modules).
If the chain complex depends on the object X in a covariant manner (meaning that any morphism X → Y induces a morphism from the chain complex of X to the chain complex of Y), then the Hn are covariant functor
s from the category that X belongs to into the category of abelian groups (or modules).
The only difference between homology and cohomology
is that in cohomology the chain complexes depend in a contravariant manner on X, and that therefore the homology groups (which are called cohomology groups in this context and denoted by Hn) form contravariant functors from the category that X belongs to into the category of abelian groups or modules.
is a chain complex such that all but finitely many 
are zero, and the others are finitely generated abelian groups (or finite dimensional vector spaces), then we can define the Euler characteristic
(using the rank
in the case of abelian groups and the Hamel dimension in the case of vector spaces). It turns out that the Euler characteristic can also be computed on the level of homology:
and, especially in algebraic topology, this provides two ways to compute the important invariant
for the object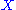 
which gave rise to the chain complex.
Every short exact sequence
of chain complexes gives rise to a long exact sequence of homology groups
All maps in this long exact sequence are induced by the maps between the chain complexes, except for the maps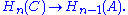
The latter are called connecting homomorphisms and are provided by the snake lemma
.
The homology group was further developed by Emmy Noether
and, independently, by Leopold Vietoris
and Walther Mayer
, in the period 1925–28.
Prior to this, topological classes in combinatorial topology
were not formally considered as abelian group
s. The spread of homology groups marked the change of terminology and viewpoint from "combinatorial topology" to "algebraic topology".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
(especially algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
and abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
), homology (in part from Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
ὁμόιος homos "identical") is a certain general procedure to associate a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s or modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
with a given mathematical object such as a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
or a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. See homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
for more background, or singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
for a concrete version for topological spaces, or group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
for a concrete version for groups.
For a topological space, the homology groups are generally much easier to compute than the homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s, and consequently one usually will have an easier time working with homology to aid in the classification of spaces.
The original motivation for defining homology groups is the commonplace observation that one aspect of the shape of an object is its holes. But because a hole is "not there", it is not immediately obvious how to define a hole, or how to distinguish between different kinds of holes. Homology is a rigorous mathematical method for detecting and categorizing holes in a shape. As it turns out, there exist subtle kinds of holes that homology cannot "see" — in which case homotopy groups may be what is needed.
Construction of homology groups
The construction begins with an object such as a topological space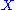, on which one first defines a chain complexChain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
encoding information about . A chain complex is a sequence of abelian groups or modules 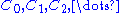connected by homomorphismsGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
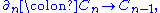which are called boundary operators. That is,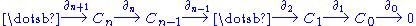where 0 denotes the trivial group and
for . It is also required that the composition of any two consecutive boundary operators be trivial. That is, for all ,i.e., the constant map to the group identity in
. This means .Now since each
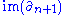is abelian, is a normal subgroup of 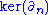. And we want to mod out by this subgroup, i.e., consider everything in equivalent and partition using this equivalence relation. The n-th homology group of X is defined to be the factor group (or quotient moduleQuotient module
In abstract algebra, given a module and a submodule, one can construct their quotient module. This construction, described below, is analogous to how one obtains the ring of integers modulo an integer n, see modular arithmetic...
)
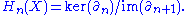
We also use the notation
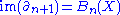and , so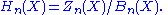Computing these two groups is usually rather difficult since they are very large groups. On the other hand, we do have tools which make the task easier.
The simplicial homology
Simplicial homology
In mathematics, in the area of algebraic topology, simplicial homology is a theory with a finitary definition, and is probably the most tangible variant of homology theory....
groups
of a simplicial complexSimplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
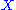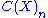are defined using the simplicial chain complex , with the free abelian group generated by the -simplices of 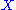. The singular homologySingular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
groups
are defined for any topological space 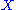, and agree with the simplicial homology groups for a simplicial complex.A chain complex is said to be exact
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
if the image of the (n + 1)-th map is always equal to the kernel of the nth map. The homology groups of
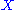therefore measure "how far" the chain complex associated to 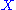is from being exact.Cohomology groups are formally similar: one starts with a cochain complex, which is the same as a chain complex but whose arrows, now denoted
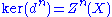point in the direction of increasing n rather than decreasing n; then the groups and 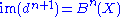follow from the same description andas before.
Examples
The motivating example comes from algebraic topologyAlgebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
: the simplicial homology
Simplicial homology
In mathematics, in the area of algebraic topology, simplicial homology is a theory with a finitary definition, and is probably the most tangible variant of homology theory....
of a simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
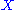. Here 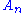is the free abelian groupFree abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
or module whose generators are the n-dimensional
oriented simplexes of
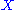. The mappings are called the boundary mappings and send the simplex with verticesVertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
to the sum
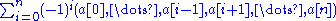
(which is considered 0 if n = 0).
If we take the modules to be over a field, then the dimension
of the n-th homology of
turns out to be the number of "holes" in at dimension n.Using this example as a model, one can define a singular homology for any topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
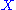. We define a chain complex for by taking to be the free abelian group (or free module) whose generators are all continuous maps from n-dimensional simplicesSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
into
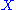. The homomorphisms arise from the boundary maps of simplices.In abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, one uses homology to define derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s, for example the Tor functor
Tor functor
In homological algebra, the Tor functors are the derived functors of the tensor product functor. They were first defined in generality to express the Künneth theorem and universal coefficient theorem in algebraic topology....
s. Here one starts with some covariant additive functor
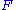and some module 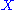. The chain complex for is defined as follows: first find a free module and a surjective homomorphism 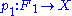. Then one finds a free module 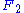and a surjective homomorphism 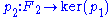. Continuing in this fashion, a sequence of free modules 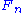and homomorphisms can be defined. By applying the functor to this sequence, one obtains a chain complex; the homology of this complex depends only on and and is, by definition, the n-th derived functor of 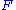, applied to 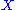.Homology functors
Chain complexes form a categoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
: A morphism from the chain complex
to the chain complex is a sequence of homomorphisms 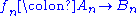such that for all n. The n-th homology Hn can be viewed as a covariant functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from the category of chain complexes to the category of abelian groups (or modules).
If the chain complex depends on the object X in a covariant manner (meaning that any morphism X → Y induces a morphism from the chain complex of X to the chain complex of Y), then the Hn are covariant functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s from the category that X belongs to into the category of abelian groups (or modules).
The only difference between homology and cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
is that in cohomology the chain complexes depend in a contravariant manner on X, and that therefore the homology groups (which are called cohomology groups in this context and denoted by Hn) form contravariant functors from the category that X belongs to into the category of abelian groups or modules.
Properties
If is a chain complex such that all but finitely many are zero, and the others are finitely generated abelian groups (or finite dimensional vector spaces), then we can define the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
(using the rank
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
in the case of abelian groups and the Hamel dimension in the case of vector spaces). It turns out that the Euler characteristic can also be computed on the level of homology:
and, especially in algebraic topology, this provides two ways to compute the important invariant
for the object 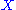which gave rise to the chain complex.Every short exact sequence
of chain complexes gives rise to a long exact sequence of homology groups
All maps in this long exact sequence are induced by the maps between the chain complexes, except for the maps
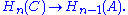The latter are called connecting homomorphisms and are provided by the snake lemmaSnake lemma
The snake lemma is a tool used in mathematics, particularly homological algebra, to construct long exact sequences. The snake lemma is valid in every abelian category and is a crucial tool in homological algebra and its applications, for instance in algebraic topology...
.
History
Homology classes were first defined rigorously by Henri Poincaré in his seminal paper "Analysis situs", J. Ecole polytech. (2) 1. 1–121 (1895).The homology group was further developed by Emmy Noether
Emmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
and, independently, by Leopold Vietoris
Leopold Vietoris
Leopold Vietoris was an Austrian mathematician and a World War I veteran who gained additional fame by becoming a supercentenarian...
and Walther Mayer
Walther Mayer
Walter Mayer was an Austrian mathematician, born 1887 in Graz, Austria.Mayer, who was Jewish, studied at the Federal Institute of Technology in Zürich and the University of Paris before receiving his doctorate in 1912 from the University of Vienna...
, in the period 1925–28.
Prior to this, topological classes in combinatorial topology
Combinatorial topology
In mathematics, combinatorial topology was an older name for algebraic topology, dating from the time when topological invariants of spaces were regarded as derived from combinatorial decompositions such as simplicial complexes...
were not formally considered as abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s. The spread of homology groups marked the change of terminology and viewpoint from "combinatorial topology" to "algebraic topology".
See also
- Simplicial homologySimplicial homologyIn mathematics, in the area of algebraic topology, simplicial homology is a theory with a finitary definition, and is probably the most tangible variant of homology theory....
- Singular homologySingular homologyIn algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
- Cellular homologyCellular homologyIn mathematics, cellular homology in algebraic topology is a homology theory for CW-complexes. It agrees with singular homology, and can provide an effective means of computing homology modules.- Definition :...
- Homology theoryHomology theoryIn mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
- Homological algebraHomological algebraHomological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
- CohomologyCohomologyIn mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...