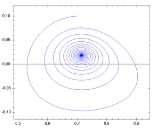
Phase space
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system
System
System is a set of interacting or interdependent components forming an integrated whole....
are represented, with each possible state of the system corresponding to one unique point in the phase space. For mechanical systems
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, the phase space usually consists of all possible values of position and momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
variables.
A plot of position and momentum variables as a function of time is sometimes called a phase plot or a phase diagram. Phase diagram
Phase diagram
A phase diagram in physical chemistry, engineering, mineralogy, and materials science is a type of chart used to show conditions at which thermodynamically distinct phases can occur at equilibrium...
, however, is more usually reserved in the physical sciences for a diagram showing the various regions of stability of the thermodynamic phases of a chemical system, which consists of pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
, temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, and composition.
In a phase space, every degree of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
or parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line
Phase line (mathematics)
In mathematics, a phase line is a diagram that shows the qualitative behaviour of an autonomous ordinary differential equation in a single variable, dy/dt = ƒ...
, while a two-dimensional system is called a phase plane
Phase plane
A phase plane is a visual display of certain characteristics of certain kinds of differential equations; it is a 2-dimensional version of the general n-dimensional phase space....
. For every possible state of the system, or allowed combination of values of the system's parameters, a point is plotted in the multidimensional space. Often this succession of plotted points is analogous to the system's state evolving over time. In the end, the phase diagram represents all that the system can be, and its shape can easily elucidate qualities of the system that might not be obvious otherwise. A phase space may contain very many dimensions. For instance, a gas containing many molecules may require a separate dimension for each particle's x, y and z positions and momenta as well as any number of other properties.
In classical mechanics the phase space co-ordinates are the generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
qi and their conjugate generalized momenta pi. The motion of an ensemble
Statistical ensemble (mathematical physics)
In mathematical physics, especially as introduced into statistical mechanics and thermodynamics by J. Willard Gibbs in 1878, an ensemble is an idealization consisting of a large number of mental copies of a system, considered all at once, each of which represents a possible state that the real...
of systems in this space is studied by classical statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. The local density of points in such systems obeys Liouville's Theorem
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
, and so can be taken as constant. Within the context of a model system in classical mechanics, the phase space coordinates of the system at any given time are composed of all of the system's dynamical variables. Because of this, it is possible to calculate the state of the system at any given time in the future or the past, through integration of Hamilton's or Lagrange's equations of motion.
Low dimensions
For simple systems, there may be as few as one or two degrees of freedom. One degree of freedom occurs when one has an autonomousAutonomous system (mathematics)
In mathematics, an autonomous system or autonomous differential equation is a system of ordinary differential equations which does not explicitly depend on the independent variable...
ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
in a single variable,
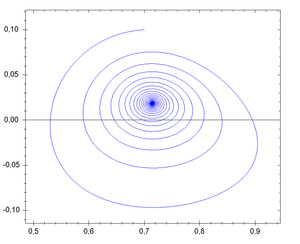
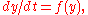 with the resulting one-dimensional system being called a phase line
with the resulting one-dimensional system being called a phase linePhase line (mathematics)
In mathematics, a phase line is a diagram that shows the qualitative behaviour of an autonomous ordinary differential equation in a single variable, dy/dt = ƒ...
, and the qualitative behaviour of the system being immediately visible from the phase line. The simplest non-trivial examples are the exponential growth model/decay (one unstable/stable equilibrium) and the logistic growth model (two equilibria, one stable, one unstable).
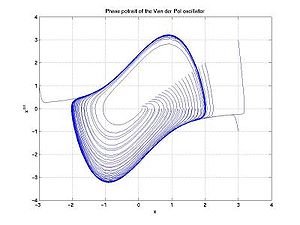
The phase space of a two-dimensional system is called a phase plane
Phase plane
A phase plane is a visual display of certain characteristics of certain kinds of differential equations; it is a 2-dimensional version of the general n-dimensional phase space....
, which occurs in classical mechanics for a single particle moving in one dimension, and where the two variables are position and velocity. In this case, a sketch of the phase portrait
Phase portrait
A phase portrait is a geometric representation of the trajectories of a dynamical system in the phase plane. Each set of initial conditions is representated by a different curve, or point....
may give qualitative information about the dynamics of the system, such as the limit-cycle
Limit-cycle
In mathematics, in the area of dynamical systems, a limit-cycle on a plane or a two-dimensional manifold is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such...
of the Van der Pol oscillator shown in the diagram.
Chaos theory
Classic examples of phase diagrams from chaos theoryChaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
are :
- the Lorenz attractorLorenz attractorThe Lorenz attractor, named for Edward N. Lorenz, is an example of a non-linear dynamic system corresponding to the long-term behavior of the Lorenz oscillator. The Lorenz oscillator is a 3-dimensional dynamical system that exhibits chaotic flow, noted for its lemniscate shape...
- parameter plane of complex quadratic polynomialComplex quadratic polynomialA complex quadratic polynomial is a quadratic polynomial whose coefficients are complex numbers.-Forms:When the quadratic polynomial has only one variable , one can distinguish its 4 main forms:...
s with Mandelbrot setMandelbrot setThe Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
.
Quantum mechanics
In quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the coordinates p and q of phase space normally become hermitian operators in a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
.
But they may alternatively retain their classical interpretation, provided functions of them compose in novel algebraic ways (through Groenewold's 1946 star product
Moyal product
In mathematics, the Moyal product, named after José Enrique Moyal, is perhaps the best-known example of a phase-space star product: an associative, non-commutative product, ∗, on the functions on ℝ2n, equipped with its Poisson bracket .This particular star product is also sometimes called...
), consistent with the uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
of quantum mechanics.
Every quantum mechanical observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
corresponds to a unique function or distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
on phase space, and vice versa, as specified by Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
(1927) and supplemented by John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
(1931); Eugene Wigner (1932); and, in a grand synthesis, by H J Groenewold
Hilbrand J. Groenewold
Hilbrand Johannes Groenewold was a Dutch theoretical physicist who pioneered the largely operator-free formulation of quantum mechanics in phase space known as phase-space quantization....
(1946).
With J E Moyal
José Enrique Moyal
José Enrique Moyal was a mathematical physicist who contributed to aeronautical engineering, electrical engineering and statistics, among other fields...
(1949), these completed the foundations of phase-space quantization
Weyl quantization
In mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
, a complete and logically autonomous reformulation of quantum mechanics. (Its modern abstractions include deformation quantization and geometric quantization
Geometric quantization
In mathematical physics, geometric quantization is a mathematical approach to defining a quantum theory corresponding to a given classical theory. It attempts to carry out quantization, for which there is in general no exact recipe, in such a way that certain analogies between the classical theory...
.)
Expectation values in phase-space quantization are obtained isomorphically to tracing operator observables with the density matrix in Hilbert space: they are obtained by phase-space integrals of observables, with the Wigner quasi-probability distribution
Wigner quasi-probability distribution
The Wigner quasi-probability distribution is a quasi-probability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics...
effectively serving as a measure.
Thus, by expressing quantum mechanics in phase space (the same ambit as for classical mechanics), the Weyl map
Weyl quantization
In mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
facilitates recognition of quantum mechanics as a deformation (generalization) of classical mechanics, with deformation parameter ħ/S, where S is the action of the relevant process. (Other familiar deformations in physics involve the deformation of classical Newtonian into relativistic mechanics, with deformation parameter v/c; or the deformation of Newtonian gravity into General Relativity, with deformation parameter Schwarzschild-radius/characteristic-dimension.)
Classical expressions, observables, and operations (such as Poisson brackets) are modified by ħ-dependent quantum corrections, as the conventional commutative multiplication applying in classical mechanics is generalized to the noncommutative star-multiplication characterizing quantum mechanics and underlying its uncertainty principle.
Thermodynamics and statistical mechanics
In thermodynamicsThermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
and statistical mechanics contexts, the term phase space has two meanings: It is used in the same sense as in classical mechanics. If a thermodynamical system consists of N particles, then a point in the 6N-dimensional phase space describes the dynamical state of every particle in that system, as each particle is associated with three position variables and three momentum variables. In this sense, a point in phase space is said to be a microstate
Microstate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
of the system. N is typically on the order of Avogadro's number
Avogadro's number
In chemistry and physics, the Avogadro constant is defined as the ratio of the number of constituent particles N in a sample to the amount of substance n through the relationship NA = N/n. Thus, it is the proportionality factor that relates the molar mass of an entity, i.e...
, thus describing the system at a microscopic level is often impractical. This leads us to the use of phase space in a different sense.
The phase space can refer to the space that is parametrized by the macroscopic states of the system, such as pressure, temperature, etc. For instance, one can view the pressure-volume diagram or entropy-temperature diagrams as describing part of this phase space. A point in this phase space is correspondingly called a macrostate. There may easily be more than one microstate with the same macrostate. For example, for a fixed temperature, the system could have many dynamic configurations at the microscopic level. When used in this sense, a phase is a region of phase space where the system in question is in, for example, the liquid
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
phase, or solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
phase, etc.
Since there are many more microstates than macrostates, the phase space in the first sense is usually a manifold of much larger dimensions than the second sense. Clearly, many more parameters are required to register every detail of the system down to the molecular or atomic scale than to simply specify, say, the temperature or the pressure of the system.
Phase Integral
In classical statistical mechanics (continuous energies) the concept ofphase space provides a classical analog to the partition function (sum
over states) known as the phase integral. Instead of summing the
Boltzmann factor over discretely spaced energy states (defined by
appropriate integer quantum numbers for each degree of freedom) one may
integrate over continuous phase space. Such integration essentially
consists of two parts: integration of the momentum component of all
degrees of freedom (momentum space) and integration of the position
component of all degrees of freedom (configuration space). Once the
phase integral is known, it may be related to the classical partition
function by multiplication of a normalization constant representing the
number of quantum energy states per unit phase space. As shown in detail
in, this normalization constant
is simply the inverse of Planck's constant raised to a power equal to the
number of degrees of freedom for the system.
See also
- Phase linePhase line (mathematics)In mathematics, a phase line is a diagram that shows the qualitative behaviour of an autonomous ordinary differential equation in a single variable, dy/dt = ƒ...
, 1-dimensional case - Phase planePhase planeA phase plane is a visual display of certain characteristics of certain kinds of differential equations; it is a 2-dimensional version of the general n-dimensional phase space....
, 2-dimensional case - Phase portraitPhase portraitA phase portrait is a geometric representation of the trajectories of a dynamical system in the phase plane. Each set of initial conditions is representated by a different curve, or point....
- Phase space methodPhase space methodIn applied mathematics, the phase space method is a technique for constructing and analyzing solutions of dynamical systems, that is, solving time-dependent differential equations. The method consists of first rewriting the equations as a system of differential equations that are first-order in...
- Parameter spaceParameter spaceIn science, a parameter space is the set of values of parameters encountered in a particular mathematical model. Often the parameters are inputs of a function, in which case the technical term for the parameter space is domain of a function....
Applications
- Optical Phase SpaceOptical phase spaceIn quantum optics, an optical phase space is a phase space in which all quantum states of an optical system are described. Each point in the optical phase space corresponds to a unique state of an optical system. For any such system, a plot of the quadratures against each other, possibly as...
- State space (controls)State space (controls)In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...
for information about state space (similar to phase state) in control engineering. - State spaceState spaceIn the theory of discrete dynamical systems, a state space is a directed graph where each possible state of a dynamical system is represented by a vertex, and there is a directed edge from a to b if and only if ƒ = b where the function f defines the dynamical system.State spaces are...
for information about state space with discrete states in computer science. - Molecular dynamicsMolecular dynamicsMolecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
Mathematics
- Cotangent bundleCotangent bundleIn mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
- Dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
- Symplectic manifoldSymplectic manifoldIn mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
- Weyl quantizationWeyl quantizationIn mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
Physics
- Classical mechanicsClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
- Hamiltonian mechanicsHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
- Lagrangian mechanicsLagrangian mechanicsLagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
- State space (physics)State space (physics)In physics, a state space is a complex Hilbert space within which the possible instantaneous states of the system may be described by a unit vector. These state vectors, using Dirac's bra-ket notation, can often be treated as vectors and operated on using the rules of linear algebra...
for information about state space in physics

