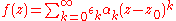
Analytic continuation
Encyclopedia
In complex analysis
, a branch of mathematics
, analytic continuation is a technique to extend the domain of a given analytic function
. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which it is initially defined becomes divergent.
The step-wise continuation technique may, however, come up against difficulties. These may have an essentially topological nature, leading to inconsistencies (defining more than one value). They may alternatively have to do with the presence of mathematical singularities. The case of several complex variables
is rather different, since singularities then cannot be isolated points, and its investigation was a major reason for the development of sheaf cohomology
.
 Suppose f is an analytic function defined on an open subset U of the complex plane
Suppose f is an analytic function defined on an open subset U of the complex plane
 . If V is a larger open subset of
. If V is a larger open subset of  , containing U, and F is an analytic function
, containing U, and F is an analytic function
defined on V such that
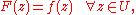
then F is called an analytic continuation of f. In other words, the restriction of F to U is the function f we started with.
Analytic continuations are unique in the following sense: if V is the connected
domain of two analytic functions F1 and F2 such that U is contained in V and for all z in U
then
on all of V. This is because F1 − F2 is an analytic function which vanishes on the open, connected domain U of f and hence must vanish on its entire domain. This follows directly from the identity theorem
for holomorphic functions.
on the small domain and then using this equation to extend the domain. Examples are the Riemann zeta function and the gamma function
.
The concept of a universal cover was first developed to define a natural domain for the analytic continuation of an analytic function
. The idea of finding the maximal analytic continuation of a function in turn led to the development of the idea of Riemann surface
s.
The power series defined above is generalized by the idea of a germ
. The general theory of analytic continuation and its generalizations are known as sheaf theory
.
be a power series converging in the disc Dr(z0) defined by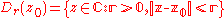 .
.
Note that without loss of generality, here and below, we will always assume that a maximal such r was chosen, even if that r is ∞. Also note that it would be equivalent to begin with an analytic function defined on some small open set. We say that the vector
is a germ
of f. The base g0 of g is z0, the stem of g is (α0, α1, α2, ...) and the top g1 of g is α0. The top of g is the value of f at z0, the bottom of g.
Any vector g = (z0, α0, α1, ...) is a germ if it represents a power series of an analytic function around z0 with some radius of convergence r > 0. Therefore, we can safely speak of the set of germs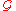 .
.
. If |h0 − g0| < r where r is the radius of convergence of g and if the power series that g and h define identical functions on the intersection of the two domains, then we say that h is generated by (or compatible with) g, and we write g ≥ h. This compatibility condition is neither transitive, symmetric nor antisymmetric. If we extend
the relation by transitivity
, we obtain a symmetric relation, which is therefore also an equivalence relation
on germs (but not an ordering). This extension by transitivity is one definition of analytic continuation. The equivalence relation will be denoted .
.
We can define a topology
on . Let r > 0, and let
. Let r > 0, and let
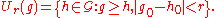
The sets Ur(g), for all r > 0 and g ∈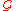 define a basis of open sets for the topology on
define a basis of open sets for the topology on 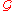 .
.
A connected component
of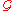 (i.e., an equivalence class) is called a sheaf
(i.e., an equivalence class) is called a sheaf
. We also note that the map φg(h) = h0 from Ur(g) to C where r is the radius of convergence of g, is a chart. The set of such charts forms an atlas for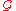 , hence
, hence 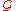 is a Riemann surface
is a Riemann surface
.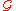 is sometimes called the universal analytic function.
is sometimes called the universal analytic function.

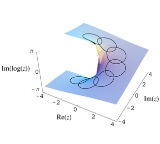
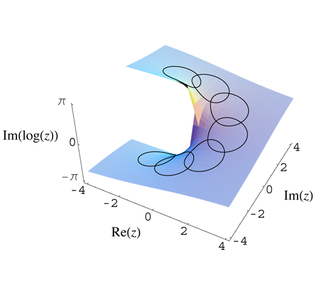
is a power series corresponding to the natural logarithm
near z = 1. This power series can be turned into a germ
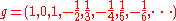
This germ has a radius of convergence of 1, and so there is a sheaf
S corresponding to it. This is the sheaf of the logarithm function.
The uniqueness theorem for analytic functions also extends to sheaves of analytic functions: if the sheaf of an analytic function contains the zero germ (i.e., the sheaf is uniformly zero in some neighborhood) then the entire sheaf is zero. Armed with this result, we can see that if we take any germ g of the sheaf S of the logarithm function, as described above, and turn it into a power series f(z) then this function will have the property that exp(f(z))=z. If we had decided to use a version of the inverse function theorem
for analytic functions, we could construct a wide variety of inverses for the exponential map, but we would discover that they are all represented by some germ in S. In that sense, S is the "one true inverse" of the exponential map.
In older literature, sheaves of analytic functions were called multi-valued functions. See sheaf
for the general concept.
Suppose D is an open set in , and f an analytic function on D. If G is a simply connected domain containing D, such that f has an analytic continuation along every path in G, starting from some fixed point a in D, then f has a direct analytic continuation to G.
, and f an analytic function on D. If G is a simply connected domain containing D, such that f has an analytic continuation along every path in G, starting from some fixed point a in D, then f has a direct analytic continuation to G.
In the above language this means that if G is a simply connected domain, and S is a sheaf whose set of base points contains G, then there exists an analytic function f on G whose germs belong to S.
with coefficients mostly zero in the precise sense that they vanish outside a sequence of exponents k(i) with
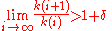
for some fixed δ > 0, the circle centre z0 and with radius the radius of convergence is a natural boundary. Such a power series defines a lacunary function
.
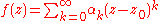 be a power series, then there exist
be a power series, then there exist 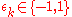 such that
such that
has the convergence disc of f around z0 as a natural boundary.
The proof of this theorem makes use of Hadamard's gap theorem.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, analytic continuation is a technique to extend the domain of a given analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which it is initially defined becomes divergent.
The step-wise continuation technique may, however, come up against difficulties. These may have an essentially topological nature, leading to inconsistencies (defining more than one value). They may alternatively have to do with the presence of mathematical singularities. The case of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
is rather different, since singularities then cannot be isolated points, and its investigation was a major reason for the development of sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
.
Initial discussion

Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
 . If V is a larger open subset of
. If V is a larger open subset of  , containing U, and F is an analytic function
, containing U, and F is an analytic functionAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
defined on V such that
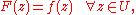
then F is called an analytic continuation of f. In other words, the restriction of F to U is the function f we started with.
Analytic continuations are unique in the following sense: if V is the connected
Connectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
domain of two analytic functions F1 and F2 such that U is contained in V and for all z in U
- F1(z) = F2(z) = f(z),
then
- F1 = F2
on all of V. This is because F1 − F2 is an analytic function which vanishes on the open, connected domain U of f and hence must vanish on its entire domain. This follows directly from the identity theorem
Identity theorem
In complex analysis, a branch of mathematics, the identity theorem for holomorphic functions states: given functions f and g holomorphic on a connected open set D, if f = g on some neighborhood of z that is in D, then f = g on D. Thus a holomorphic function is completely determined by its values on...
for holomorphic functions.
Applications
A common way to define functions in complex analysis proceeds by first specifying the function on a small domain only, and then extending it by analytic continuation. In practice, this continuation is often done by first establishing some functional equationFunctional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
on the small domain and then using this equation to extend the domain. Examples are the Riemann zeta function and the gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
The concept of a universal cover was first developed to define a natural domain for the analytic continuation of an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
. The idea of finding the maximal analytic continuation of a function in turn led to the development of the idea of Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s.
The power series defined above is generalized by the idea of a germ
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
. The general theory of analytic continuation and its generalizations are known as sheaf theory
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
.
Formal definition of a germ
Letbe a power series converging in the disc Dr(z0) defined by
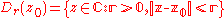 .
.Note that without loss of generality, here and below, we will always assume that a maximal such r was chosen, even if that r is ∞. Also note that it would be equivalent to begin with an analytic function defined on some small open set. We say that the vector
- g = (z0, α0, α1, α2, ...)
is a germ
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
of f. The base g0 of g is z0, the stem of g is (α0, α1, α2, ...) and the top g1 of g is α0. The top of g is the value of f at z0, the bottom of g.
Any vector g = (z0, α0, α1, ...) is a germ if it represents a power series of an analytic function around z0 with some radius of convergence r > 0. Therefore, we can safely speak of the set of germs
 .
.The topology of the set of germs
Let g and h be germsGerm (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
. If |h0 − g0| < r where r is the radius of convergence of g and if the power series that g and h define identical functions on the intersection of the two domains, then we say that h is generated by (or compatible with) g, and we write g ≥ h. This compatibility condition is neither transitive, symmetric nor antisymmetric. If we extend
Transitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
the relation by transitivity
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
, we obtain a symmetric relation, which is therefore also an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on germs (but not an ordering). This extension by transitivity is one definition of analytic continuation. The equivalence relation will be denoted
 .
.We can define a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on
 . Let r > 0, and let
. Let r > 0, and let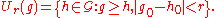
The sets Ur(g), for all r > 0 and g ∈
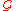 define a basis of open sets for the topology on
define a basis of open sets for the topology on 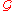 .
.A connected component
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
of
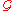 (i.e., an equivalence class) is called a sheaf
(i.e., an equivalence class) is called a sheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
. We also note that the map φg(h) = h0 from Ur(g) to C where r is the radius of convergence of g, is a chart. The set of such charts forms an atlas for
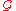 , hence
, hence 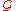 is a Riemann surface
is a Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
.
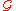 is sometimes called the universal analytic function.
is sometimes called the universal analytic function.Examples of analytic continuation

is a power series corresponding to the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
near z = 1. This power series can be turned into a germ
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
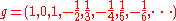
This germ has a radius of convergence of 1, and so there is a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
S corresponding to it. This is the sheaf of the logarithm function.
The uniqueness theorem for analytic functions also extends to sheaves of analytic functions: if the sheaf of an analytic function contains the zero germ (i.e., the sheaf is uniformly zero in some neighborhood) then the entire sheaf is zero. Armed with this result, we can see that if we take any germ g of the sheaf S of the logarithm function, as described above, and turn it into a power series f(z) then this function will have the property that exp(f(z))=z. If we had decided to use a version of the inverse function theorem
Inverse function theorem
In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
for analytic functions, we could construct a wide variety of inverses for the exponential map, but we would discover that they are all represented by some germ in S. In that sense, S is the "one true inverse" of the exponential map.
In older literature, sheaves of analytic functions were called multi-valued functions. See sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
for the general concept.
Monodromy theorem
The monodromy theorem gives a sufficient condition for the existence of a direct analytic continuation (i.e., an extension of an analytic function to an analytic function on a bigger set).Suppose D is an open set in
 , and f an analytic function on D. If G is a simply connected domain containing D, such that f has an analytic continuation along every path in G, starting from some fixed point a in D, then f has a direct analytic continuation to G.
, and f an analytic function on D. If G is a simply connected domain containing D, such that f has an analytic continuation along every path in G, starting from some fixed point a in D, then f has a direct analytic continuation to G.In the above language this means that if G is a simply connected domain, and S is a sheaf whose set of base points contains G, then there exists an analytic function f on G whose germs belong to S.
Hadamard's gap theorem
For a power serieswith coefficients mostly zero in the precise sense that they vanish outside a sequence of exponents k(i) with
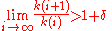
for some fixed δ > 0, the circle centre z0 and with radius the radius of convergence is a natural boundary. Such a power series defines a lacunary function
Lacunary function
In analysis, a lacunary function, also known as a lacunary series, is an analytic function that cannot be analytically continued anywhere outside the radius of convergence within which it is defined by a power series...
.
Polya's theorem
Let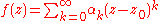 be a power series, then there exist
be a power series, then there exist 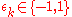 such that
such thathas the convergence disc of f around z0 as a natural boundary.
The proof of this theorem makes use of Hadamard's gap theorem.
External links
- Analytic Continuation at MathPages